Загрузить PDF
Загрузить PDF
Последовательность Фибоначчи – это ряд чисел, в котором каждое последующее число равно сумме двух предыдущих чисел. Числовые последовательности часто встречаются в природе и искусстве в виде спиралей и «золотого сечения». Самый простой способ вычислить последовательность Фибоначчи – это создать таблицу, но такой метод не применим к большим последовательностям. Например, если нужно определить 100-й член последовательности, лучше воспользоваться формулой Бине.
-
1
Нарисуйте таблицу с двумя столбцами. Количество строк таблицы зависит от количества чисел последовательности Фибоначчи, которые нужно найти.
- Например, если нужно найти пятое число последовательности, нарисуйте таблицу с пятью строками.
- Используя таблицу, нельзя найти некоторое случайное число без вычисления всех предыдущих чисел. Например, если нужно найти 100-е число последовательности, нужно вычислить все числа: от первого до 99-ого. Поэтому таблица применима только для нахождения первых чисел последовательности.
-
2
В левом столбце напишите порядковые номера членов последовательности. То есть напишите цифры по порядку, начиная с единицы.
- Такие цифры определяют порядковые номера членов (чисел) последовательности Фибоначчи.
- Например, если нужно найти пятое число последовательности, в левой колонке напишите следующие цифры: 1, 2, 3, 4, 5. То есть нужно найти с первого по пятое число последовательности.
-
3
В первой строке правой колонки напишите 1. Это первое число (член) последовательности Фибоначчи.
- Имейте в виду, что последовательность Фибоначчи всегда начинается с 1. Если последовательность начинается с другого числа, вы неправильно вычислили все числа вплоть до первого.
-
4
К первому члену (1) прибавьте 0. Получится второе число последовательности.
- Запомните: чтобы найти любое число последовательности Фибоначчи, просто сложите два предыдущих числа.
- Чтобы создать последовательность, не забудьте о 0, который стоит перед 1 (первым членом), поэтому 1 + 0 = 1.
-
5
Сложите первый (1) и второй (1) члены. Получится третье число последовательности.
- 1 + 1 = 2. Третий член равен 2.
-
6
Сложите второй (1) и третий (2) члены, чтобы получить четвертое число последовательности.
- 1 + 2 = 3. Четвертый член равен 3.
-
7
Сложите третий (2) и четвертый (3) члены. Получится пятое число последовательности.
- 2 + 3 = 5. Пятый член равен 5.
-
8
Сложите два предыдущих числа, чтобы найти любое число последовательности Фибоначчи. Этот метод основан на формуле:
.[1]
Эта формула не является замкнутой, поэтому при помощи этой формулы нельзя найти любой член последовательности без вычисления всех предыдущих чисел.Реклама
-
1
-
2
В формулу подставьте порядковый номер числа (вместо
).
– это порядковый номер любого искомого члена последовательности.
-
3
В формулу подставьте золотое сечение. Золотое сечение приблизительно равно 1,618034; подставьте в формулу это число.[5]
-
4
Вычислите выражение в скобках. Не забывайте про правильный порядок выполнения математических операций, в котором выражение в скобках вычисляется в первую очередь:
.
-
5
Возведите числа в степени. Возведите в соответствующие степени два числа, которые находятся в числителе.
-
6
Вычтите два числа. Перед тем как приступить к делению, вычтите числа, которые находятся в числителе.
-
7
Полученный результат разделите на квадратный корень из 5. Квадратный корень из 5 приблизительно равен 2,236067.
- В нашем примере:
.
- В нашем примере:
-
8
Полученный результат округлите до ближайшего целого числа. Последний результат будет десятичной дробью, которая близка к целому числу. Такое целое число представляет собой число последовательности Фибоначчи.
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.[6]
- В нашем примере вы получили десятичную дробь 5,000002. Округлите ее до ближайшего целого числа и получите пятое число последовательности Фибоначчи, которое равно 5.
Реклама
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.[6]
Об этой статье
Эту страницу просматривали 27 790 раз.
Была ли эта статья полезной?
Download Article
Download Article
The Fibonacci sequence is a pattern of numbers generated by summing the previous two numbers in the sequence.[1]
The numbers in the sequence are frequently seen in nature and in art, represented by spirals and the golden ratio. The easiest way to calculate the sequence is by setting up a table; however, this is impractical if you are looking for, for example, the 100th term in the sequence, in which case Binet’s formula can be used.
-
1
Set up a table with two columns. The number of rows will depend on how many numbers in the Fibonacci sequence you want to calculate.[2]
- For example, if you want to find the fifth number in the sequence, your table will have five rows.
- When using the table method, you cannot find a random number farther down in the sequence without calculating all the number before it. For example, if you want to find the 100th number in the sequence, you have to calculate the 1st through 99th numbers first. This is why the table method only works well for numbers early in the sequence.
-
2
Enter the sequence of terms in the left column. This means just entering a sequence of sequential ordinal numbers, beginning with «1st.»
- The term refers to the position number in the Fibonacci sequence.
- For example, if you want to figure out the fifth number in the sequence, you will write 1st, 2nd, 3rd, 4th, 5th down the left column. This will show you what the first through fifth terms in the sequence are.
Advertisement
-
3
Enter 1 in the first row of the right-hand column. This is the starting point for the Fibonacci Sequence. In other words, the first term in the sequence is 1.
- The correct Fibonacci sequence always starts on 1. If you begin with a different number, you are not finding the proper pattern of the Fibonacci sequence.
-
4
Add the first term (1) and 0. This will give you the second number in the sequence.
- Remember, to find any given number in the Fibonacci sequence, you simply add the two previous numbers in the sequence.
- To create the sequence, you should think of 0 coming before 1 (the first term), so 1 + 0 = 1.
-
5
Add the first term (1) and the second term (1). This will give you the third number in the sequence.[3]
- 1 + 1 = 2. The third term is 2.
-
6
Add the second term (1) and the third term (2) to get the fourth number in the sequence.
- 1 + 2 = 3. The fourth term is 3.
-
7
Add the third term (2) and the fourth term (3). This will give you the fifth number in the sequence.[4]
- 2 + 3 = 5. The fifth term is 5.
-
8
Sum the previous two numbers to find any given number in the Fibonacci Sequence. When you use this method, you are using the formula
.[5]
Since this is not a closed formula, however, you cannot use it to calculate any given term in the sequence without calculating all the previous numbers.[6]
Advertisement
-
1
-
2
Plug the number for
into the formula. The
represents whatever term you are looking for in the sequence.
-
3
Substitute the golden ratio into the formula. You can use 1.618034 as an approximation of the golden ratio.[10]
-
4
Complete the calculations in parentheses. Remember to use the order of operations by completing the calculation in parentheses first:
.
-
5
Calculate the exponents. Multiply the two parenthetical numbers in the numerator by the appropriate exponent.
-
6
Complete the subtraction. Before you divide, you need to subtract the two numbers in the numerator.
-
7
Divide by the square root of 5. The square root of 5, rounded, is 2.236067.[11]
- In the example problem,
.
- In the example problem,
-
8
Round to the nearest whole number. Your answer will be a decimal, but it will be very close to a whole number. This whole number represents the number in the Fibonacci sequence.
- If you used the complete golden ratio and did no rounding, you would get a whole number. It’s more practical to round, however, which will result in a decimal.[12]
- In the example, after using a calculator to complete all the calculations, your answer will be approximately 5.000002. Rounding to the nearest whole number, your answer, representing the fifth number in the Fibonacci sequence, is 5.
- If you used the complete golden ratio and did no rounding, you would get a whole number. It’s more practical to round, however, which will result in a decimal.[12]
Advertisement
Add New Question
-
Question
Is «Fibonacci» an English word?
Danoyachtcapt
Top Answerer
No, it is the name of mathematician Leonardo of Pisa.
-
Question
How do I deduce Binet’s fibonacci number formula?
Orangejews
Community Answer
One way is to interpret the recursion as a matrix multiplication. Take a vector of two consecutive terms like (13, 8), multiply by a transition matrix M = (1,1; 1,0) to get the next such vector (21,13). That gives a formula involving M^n, but if you diagonalize M, computing M^n is easy and that formula pops right out.
-
Question
Who discovered this sequence?
Leonardo Bonacci
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate the Fibonacci sequence up to the 5th term, start by setting up a table with 2 columns and writing in 1st, 2nd, 3rd, 4th, and 5th in the left column. Next, enter 1 in the first row of the right-hand column, then add 1 and 0 to get 1. Write 1 in the column next to “2nd,” then add the 1st and 2nd term to get 2, which is the 3rd number in the sequence. Continue this pattern of adding the 2 previous numbers in the sequence to get 3 for the 4th term and 5 for the 5th term. To learn more, including how to calculate the Fibonacci sequence using Binet’s formula and the golden ratio, scroll down.
Did this summary help you?
Thanks to all authors for creating a page that has been read 246,510 times.
Did this article help you?
Задача: посчитать N-е число последовательности, в которой каждый элемент равен сумме двух предыдущих. Такая последовательность называется последовательностью Фибоначчи: 1, 1, 2, 3, 5, 8…
Очень часто на разнообразных олимпиадах попадаются задачи вроде этой, которые, как думается на первый взгляд, можно решить с помощью простого перебора. Но если мы подсчитаем количество возможных вариантов, то сразу убедимся в неэффективности такого подхода: например, простая рекурсивная функция, приведенная ниже, будет потреблять существенные ресурсы уже на 30-ом числе Фибоначчи, тогда как на олимпиадах время решения часто ограничено 1-5 секундами.
int fibo(int n)
{
if (n == 1 || n == 2) {
return 1;
} else {
return fibo(n - 1) + fibo(n - 2);
}
}Давайте подумаем, почему так происходит. Например, для вычисления fibo(30) мы сначала вычисляем fibo(29) и fibo(28). Но при этом наша программа «забывает», что fibo(28) мы уже вычисляли при поиске fibo(29).
Основная ошибка такого подхода «в лоб» в том, что одинаковые значения аргументов функции исчисляются многократно — а ведь это достаточно ресурсоемкие операции. Избавиться от повторяющихся вычислений нам поможет метод динамического программирования — это прием, при использовании которого задача разбивается на общие и повторяющиеся подзадачи, каждая из которых решается только 1 раз — это значительно повышает эффективность программы. Этот метод подробно описан в нашей статье, там же есть и примеры решения других задач.
Самый просто вариант улучшения нашей функции — запоминать, какие значения мы уже вычисляли. Для этого нужно ввести дополнительный массив, который будет служить как бы «кэшем» для наших вычислений: перед вычислением нового значения мы будем проверять, не вычисляли ли его раньше. Если вычисляли, то будем брать из массива готовое значение, а если не вычисляли — придётся считать его на основе предыдущих и запоминать на будущее:
int cache[100];
int fibo(int n)
{
if (cache[n] == 0) {
if (n == 1 || n == 2) {
cache[n] = 1;
} else {
cache[n] = fibo(n - 1) + fibo(n - 2);
}
}
return cache[n];
}Так как в данной задаче для вычисления N-ого значения нам гарантированно понадобится (N-1)-е, то не составит труда переписать формулу в итерационный вид — просто будем заполнять наш массив подряд до тех пор, пока не дойдём до нужной ячейки:
cache[0] = 1;
cache[1] = 1;
for (int i = 2; i <= n; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
cout << cache[n-1];Теперь мы можем заметить, что когда мы вычисляем значение F(N), то значение F(N-3) нам уже гарантированно никогда не понадобится. То есть нам достаточно хранить в памяти лишь два значения — F(N-1) и F(N-2). Причём, как только мы вычислили F(N), хранение F(N-2) теряет всякий смысл. Попробуем записать эти размышления в виде кода:
//Два предыдущих значения:
int cache1 = 1;
int cache2 = 1;
//Новое значение
int cache3;
for (int i = 2; i <= n; i++) {
cache3 = cache1 + cache2; //Вычисляем новое значение
//Абстрактный cache4 будет равен cache3+cache2
//Значит cache1 нам уже не нужен?..
//Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации.
//cache5 = cache4 - cache3 => через итерацию потеряет актуальность cache2, т.е. он и должен стать cache1
//Иными словами, cache1 -- f(n-2), cache2 -- f(n-1), cache3 -- f(n).
//Пусть N=n+1 (номер, который мы вычисляем на следующей итерации). Тогда n-2=N-3, n-1=N-2, n=N-1.
//В соответствии с новыми реалиями мы и переписываем значения наших переменных:
cache1 = cache2;
cache2 = cache3;
}
cout << cache3;Бывалому программисту понятно, что код выше, в общем-то ерунда, так как cache3 никогда не используется (он сразу записывается в cache2), и всю итерацию можно переписать, используя всего одно выражение:
cache[0] = 1;
cache[1] = 1;
for (int i = 2; i <= n; i++) {
cache[i%2] = cache[0] + cache[1];
//При i=2 устареет 0-й элемент
//При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый
//При i=4 последним элементом мы обновляли cache[1], значит ненужное старьё сейчас в cache[0]
//Интуитивно понятно, что так будет продолжаться и дальше
}
cout << cache[n%2];Для тех, кто не может понять, как работает магия с остатком от деления, или просто хочет увидеть более неочевидную формулу, существует ещё одно решение:
int x = 1;
int y = 1;
for (int i = 2; i < n; i++) {
y = x + y;
x = y - x;
}
cout << "Число Фибоначчи: " << y;Попробуйте проследить за выполнением этой программы: вы убедитесь в правильности алгоритма.
P.S. Вообще, существует единая формула для вычисления любого числа Фибоначчи, которая не требует никаких итераций или рекурсии:
const double SQRT5 = sqrt(5);
const double PHI = (SQRT5 + 1) / 2;
int fibo(int n){
return int(pow(PHI, n) / SQRT5 + 0.5);
}Но, как можете догадаться, подвох в том, что цена вычисления степеней нецелых чисел довольно велика, как и их погрешность.
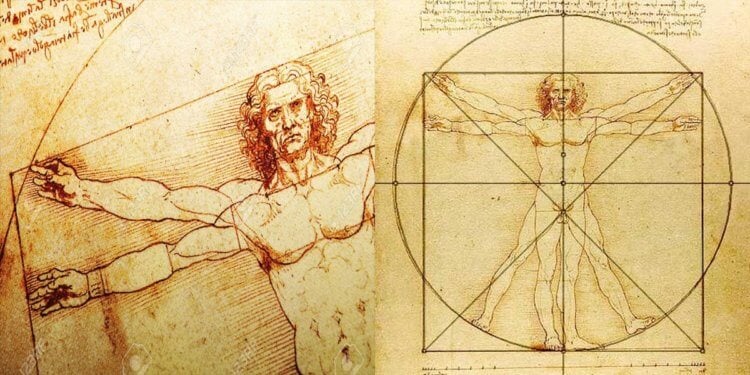
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Содержание
- 1 Кто такой Фибоначчи?
- 2 Последовательность Фибоначчи
- 3 Где используется число Фибоначчи
- 4 Что такое золотое сечение
- 5 Что такое спираль Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на предыдущее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Читайте также: Найдено самое длинное простое число Мерсенна, состоящее из 22 миллионов цифр
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
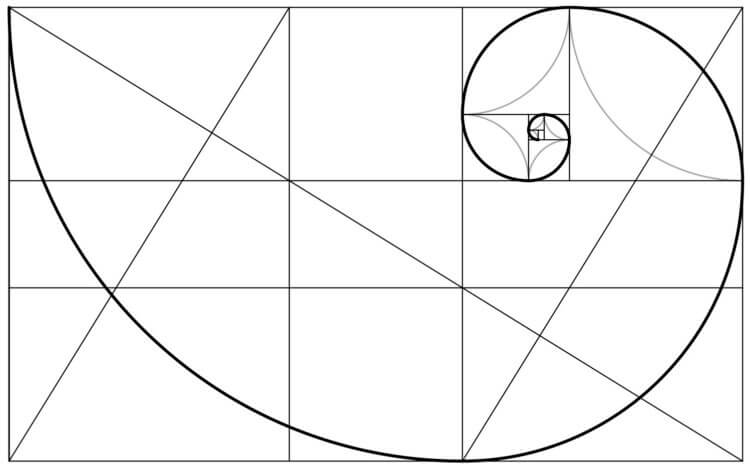
Так выглядит «золотое сечение»
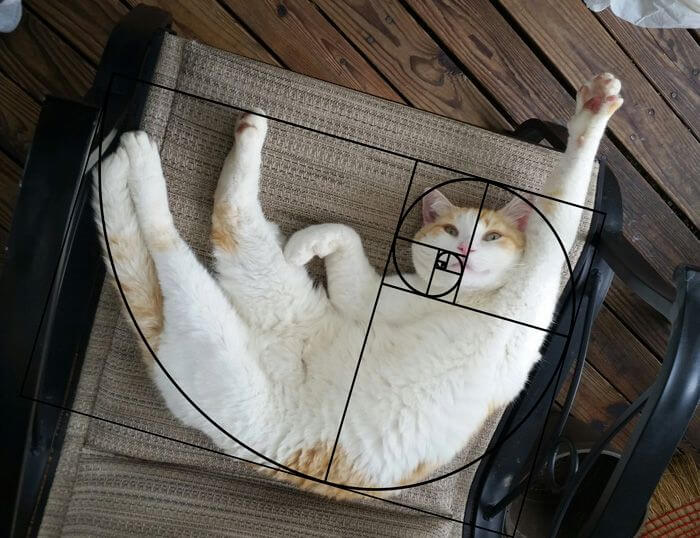
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Что такое спираль Фибоначчи
Золотая спираль или спираль Фибоначчи — это логарифмическая спираль. Ее коэффициент роста равен φ4, где φ — золотое сечение. Он показывает, во сколько раз изменился полярный радиус спирали при повороте на угол 360 градусов.
А вот еще один вопрос, имеющий отношение к Фибоначчи: почему от красивых вещей люди становятся счастливее
Эта спираль называется так из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ, которые принято называть золотыми. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве спираль, построенная по методу Дюрера, отлично подошла для решения своих задач.
Вычисление n-го числа Фибоначчи — популярная задача, которая на практике почти не встречается, но часто прменяется в обучающих целях, а также на собеседованиях. Задача очень проста, но решить ее можно несколькими алгоритмами, причем время выполнения таких алгоритмов может сильно различаться между собой.
Понятие числа Фибоначчи:
Итак, простой пример последовательности Фибоначчи (каждое последующее число равно сумме двух предыдущих):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... .
Рекуррентное соотношение таково:
F(0) = 0,
F(1) = 1,
F(i) = F(i−1) + F(i−2), где i >= 2.
Первый способ
Самый простой алгоритм для вычисления такого числа, который дается во всех книжках, это алгоритм основанный на рекурсии:
1 2 3 4 5 6 7 8 |
|
Это простой, но и самый неэффективный алгоритм, так как время алгоритма растет экспоненциально — O(2^n).
Рекурсивное дерево вызовов выглядит следующим образом:
Второй способ
Второй способ основан на принципе с сохранением каждого предыдущего числа последовательности в массиве. Такой алгоритм требует уже линейное время — O(n) на выполнение и дополнительное количество памяти для хранения всего массива чисел — O(n):
1 2 3 4 5 6 7 8 9 10 11 |
|
Третий способ
Третий способ похож на первый, за исключением того, что, мы будем хранить не весь массив вычисленных чиел, а только предыдущие два. Таким образом, колчиство дополнительной памяти сократится до O(1):
1 2 3 4 5 6 7 8 9 10 11 12 13 |
|