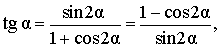Как найти сумму тангенсов всех углов - AvtoShod.ru

Формулы тангенса суммы и разности углов устанавливают соотношение между тангенсом общей суммы или разности аргументов и тангенсами отдельных аргументов — слагаемых.

При всех допустимых значениях аргументов справедливы формулы:

тангенса суммы аргументов:

tg(α+β)=tgα+tgβ1−tgα⋅tgβ

; (1)

тангенса разности аргументов:

tg(α−β)=tgα−tgβ1+tgα⋅tgβ

. (2)

Оговорка о допустимых значениях аргументов означает, что все тангенсы имеют смысл, т. е. выполняются условия:

α+β≠π2+πm,m∈ℤ

, для формулы (1),

α−β≠π2+πm,m∈ℤ

, для формулы (2).

Эти формулы очень важны и широко применяются не только в математике, но и в физике — особенно в радиотехнике.

Вывод формул естественным образом получается из определения функции тангенса и использования уже известных формул синуса и косинуса суммы и разности аргументов.

Докажем формулу тангенса суммы аргументов. Имеем:

tg(α+β)=sin(α+β)cos(α+β)=sinα⋅cosβ+cosα⋅sinβcosα⋅cosβ−sinα⋅sinβ

Разделим каждое из слагаемых числителя и знаменателя на

cosα⋅cosβ

учитывая, что значение дроби от этого не изменится и что

cosα⋅cosβ≠0

из принятых выше условий

для допустимых значений аргументов, т. е.

α≠π2+πk,β≠π2+πnk,n∈ℤ

. Тогда:

tg(α+β)=sin(α+β)cos(α+β)=sinα⋅cosβ+cosα⋅sinβcosα⋅cosβ−sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ+cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ−sinα⋅sinβcosα⋅cosβ=tgα+tgβ1−tgα⋅tgβ

— что и требовалось доказать.

Аналогично доказывается формула тангенса разности аргументов:

tg(α−β)=sin(α−β)cos(α−β)=sinα⋅cosβ−cosα⋅sinβcosα⋅cosβ+sinα⋅sinβ=sinα⋅cosβcosα⋅cosβ−cosα⋅sinβcosα⋅cosβcosα⋅cosβcosα⋅cosβ+sinα⋅sinβcosα⋅cosβ=tgα−tgβ1+tgα⋅tgβ.

Источник

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Сумма тангенсов

Примеры решения задач

ПРИМЕР 1

Задание

Проверить, что $text{tg}15^{circ}+text{tg}60^{circ}=2$

Доказательство

Применим формулу суммы тангенсов

$[text{tg}15^{circ}+text{tg}60^{circ}=frac{sin (15^{circ}+60^{circ})}{cos 15^{circ}cos 60^{circ}}=frac{sin 75^{circ}}{cos 15^{circ}cos 60^{circ}}]$

Представим $cos 15^{circ}$ в виде $cos 15^{circ}=cos (90^{circ}-75^{circ})=sin 75^{circ}$ и подставим в предыдущее равенство:

$[frac{sin 75^{circ}}{cos 15^{circ}cos 60^{circ}}=frac{sin 75^{circ}}{sin 75^{circ}cos 60^{circ}}=frac{1}{cos 60^{circ}}=2]$

т.е.

$[text{tg}15^{circ}+text{tg}60^{circ}=2]$

Что и требовалось доказать.

Понравился сайт? Расскажи друзьям!

Нужна помощь с
решением задач?

Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.

Источник

Сумма тангенсов

ОПРЕДЕЛЕНИЕ

Сумма тангенсов двух углов (
alpha
) и (
beta
) равна отношению синуса суммы (
alpha+beta
) к произведению косинусов этих углов:

(
operatorname{tg} alpha+operatorname{tg} beta=frac{sin (alpha+beta)}{cos alpha cdot cos beta}
)

Примеры решения задач

ПРИМЕР 1

Задание

Проверить, что (
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)

Доказательство

Применим формулу суммы тангенсов

(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=frac{sin left(15^{circ}+60^{circ}right)}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}
)

Представим (
cos 15^{circ}
) в (
cos 15^{circ}=cos left(90^{circ}-75^{circ}right)=sin 75^{circ}
) и подставим в предыдущее равенство: (
frac{sin 75^{circ}}{cos 15^{circ} cos 60^{circ}}=frac{sin 75^{circ}}{sin 75^{circ} cos 60^{circ}}=frac{1}{cos 60^{circ}}=2
)

т.е.

(
operatorname{tg} 15^{circ}+operatorname{tg} 60^{circ}=2
)

Что и требовалось доказать.

ПРИМЕР 2

Задание

Найти значение выражения (
operatorname{tg}^{3 pi}+operatorname{tg} frac{pi}{8}
)

Решение

Представим сумму разность в виде

(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=frac{sin left(frac{3 pi}{8}+frac{pi}{8}right)}{cos frac{3 pi}{8} cdot cos frac{pi}{8}}=frac{sin frac{pi}{2}}{frac{1}{2}left(cos frac{pi}{4}+cos frac{pi}{2}right)}=frac{1}{frac{1}{2}left(frac{sqrt{2}}{2}+0right)}=frac{4}{sqrt{2}}=2 sqrt{2}
)

Ответ

(
operatorname{tg} frac{3 pi}{8}+operatorname{tg} frac{pi}{8}=2 sqrt{2}
)

Источник

Основные тригонометрические формулы

Содержание

Справочник по математике для школьников тригонометрия связи между тригонометрическими функциями

Связи между тригонометрическими функциями одного угла

Тригонометрические функции суммы и разности двух углов

Тригонометрические функции двойного угла

Формулы понижения степени для квадратов тригонометрических функций

Формулы понижения степени для кубов синуса и косинуса

Выражение тангенса угла через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

Преобразование произведения тригонометрических функций в сумму

Выражение тригонометрических функций через тангенс половинного угла

Тригонометрические функции тройного угла

Связи между тригонометрическими функциями одного угла

Тригонометрические функции суммы и разности двух углов

Тригонометрические функции двойного угла

Формула	Название формулы
sin 2α = 2 sin α cos α	Синус двойного угла
cos 2α = cos ²α – sin²α cos 2α = 2cos ²α – 1 cos 2α = 1 – 2sin ²α	Косинус двойного угла
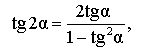	Тангенс двойного угла

Синус двойного угла

sin 2α = 2 sin α cos α

Косинус двойного угла

cos 2α = cos ²α – sin²α

cos 2α = 2cos ²α – 1

cos 2α = 1 – 2sin ²α

Тангенс двойного угла

Основные тригонометрические формулы тригонометрические функции двойного угла

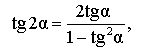Формулы понижения степени для квадратов тригонометрических функций

Формула	Название формулы
	Выражение квадрата синуса через косинус двойного угла
	Выражение квадрата косинуса через косинус двойного угла
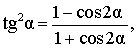	Выражение квадрата тангенса через косинус двойного угла

Формулы понижения степени для кубов синуса и косинуса

Формула	Название формулы
	Выражение куба синуса через синус угла и синус тройного угла
	Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение куба синуса через синус угла и синус тройного угла

Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение тангенса через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

Сумма синусов

Разность синусов

Сумма косинусов

Разность косинусов

Сумма тангенсов

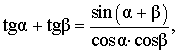Основные тригонометрические формулы преобразование суммы тригонометрических функций в произведение

Разность тангенсов

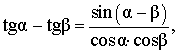Преобразование произведения тригонометрических функций в сумму

Произведение синусов

Произведение косинусов

Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

Формула	Название формулы
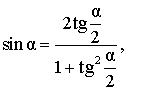	Выражение синуса угла через тангенс половинного угла
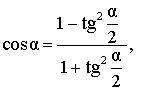	Выражение косинуса угла через тангенс половинного угла
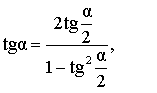	Выражение тангенса угла через тангенс половинного угла

Тригонометрические функции тройного угла

Формула	Название формулы
sin 3α = 3sin α – 4sin³α	Синус тройного угла
cos 3α = 4cos³α –3cos α	Косинус тройного угла
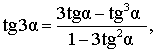	Тангенс тройного угла

Синус тройного угла

sin 3α = 3sin α – 4sin³α

Косинус тройного угла

cos 3α = 4cos³α –3cos α

Тангенс тройного угла

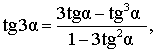Основные тригонометрические формулы тригонометрические функции тройного угла

Источник

Формулы суммы и разности углов тригонометрических функций онлайн

С помощю этого онлайн калькулятора можно получить формулы суммы и разности углов тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, нажав на «sin», выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.

Формулы суммы и разности углов тригонометрических функций − теория, доказательство, примеры

Выведем формулы суммы и разности углов тригонометрических функций. Начнем с формулы

Как мы знаем, угол между векторами не может быть больше 180° (π). На рисунке Рис.1 угол между векторами и равен . На рисунке Рис.2 угол между векторами и равен .

Рассмотрим, теперь косинусы этих углов. Из формул приведения мы знаем (подпрбнее о формулах приведения смотрите на странице Формулы приведения тригонометрических функций онлайн):

Cкалярное произведение векторов и равно:

Так как точка имеет координаты , а имеет координаты (смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов и по координатам равно:

Поскольку левые части формул (2) и (3) равны, то равны и правые части этих формул. Следовательно выполнено равенство (1).

Докажем, далее, справедливость следующей формулы

Представим косинус суммы углов α и β в виде косинуса разности двух углов и воспользуемся формулой (1) и тем, что косинус четная функция а синус нечетная функция:

Перейдем к доказательству формул синусов суммы и разности углов:

Для доказательства формулы (5) воспользуемся формулами приведения тригонометрических функций и формулой (1):

Для доказательства формулы (6), представим разность углов в виде суммы и воспользуемся тем, что косинус четная функция а синус нечетная функция:

Формулы тангенса суммы и разности углов имееют следующий вид:

Докажем формулу (7):

Разделим числитель и знаменатель дроби в правой части уравнения (9) на (, ):