Как найти сумму ряда с синусом - AvtoShod.ru - решение различных проблем

Asked
3 years, 8 months ago

Viewed
48 times

$begingroup$

I am struggling to find the proof of a sine series.

The series is as follows:

$$sum_{n=0}^{infty} dfrac{sin(2n+1)x}{2n+1} = dfrac{pi}{4}$$

Note: $x neq npi$

Can you help me with a proof or a direction I should look in? Thank you.

Robert Z

143k12 gold badges99 silver badges185 bronze badges

asked Sep 8, 2019 at 7:09

$endgroup$

$begingroup$

It should be
$$sum_{n=0}^{infty} dfrac{sin((2n+1)x)}{2n+1}=begin{cases}
0 & text{if $x=kpi$ with $kin mathbb{Z}$,}\
frac{pi}{4}cdotmathrm{sign}(sin(x)) & text{otherwise.}
end{cases}$$

Hint. Evaluate the Fourier series of the odd function $mathrm{sign}(x)$.

answered Sep 8, 2019 at 7:28

Robert ZRobert Z

143k12 gold badges99 silver badges185 bronze badges

$endgroup$

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Необходимо вычислить сумму Σ(k=1; n) (Sin (kx))^2 . Подскажите, пожалуйста, подробное решение, т.к. перерешиваю уже не один раз, а ответ все равно n/2 — ((Sin((n+1)x) * Cos(nx))/(2Sin(x)), что, согласно задачнику, неверно.

тут что-то с логикой мысли)

если перерешиваете и неверно, то покажите решение то. или я какую-то ерунду пишу))

=1/2Σ(k=1; n) (1 — cos (2kx)) = n/2 — (1/(2sinx))Σ(k=1; n) (cos(2kx)sin(x)) = n/2 — (1/(4sinx))Σ(k=1; n)(sin((2k-1)x)+sin((2k+1)x)) = n/2 — (sin((2n+1)x) +sin(x))/(4sinx) = n/2 — (sin((n+1)x)cos(nx))/(2sinx)

@Morgan, идея правильная. Только почему там после телескопической суммы осталась сумма двух синусов, а не их разность? Да и под знаком суммы до того у Вас почему-то сумма синусов стоит. Короче, пишите аккуратно.

Источник

Формулы и уравнения рядов

Числовые ряды
Функциональные ряды
Тригонометрические ряды. Ряд Фурье

Примеры решения рядов здесь.

Числовые ряды

Факториал и двойные факториалы:

$n{!}=sqrt{2*{pi}*n}*(n/e)^n$ — формула Стирлинга.

Геометрическая прогрессия:

$b_n=b_1*q^{n-1},~S_n={b_1*(1-q^n)}/{1-q},~S={b_1}/{1-q},$ |q|<1.

Основные определения и теоремы о рядах:

{u_n} — заданная бесконечная числовая последовательность,

$sum{n=1}{infty}{u_n}=u_1+u_2+...+u_n+...$ — числовой ряд,
u_n — члены ряда,
– частичные суммы ряда.

Сумма ряда:

${exists}S=lim{n{right}infty}{S_n}$ $sum{n=1}{infty}{u_n}$ сходится, S — сумма ряда.

$S_n{right}infty$ или ряд сходится и суммы нет.

Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).

Свойства сходящихся рядов:

${exists}sum{n=1}{infty}{u_n}=S~doubleright~sum{n=1}{infty}{Cu_n}=CS$

${exists}sum{n=1}{infty}{a_n}=A,~sum{n=1}{infty}{b_n}=B~doubleright~sum{n=1}{infty}{a_n+b_n}=A{pm}B.$

Теоремы сравнения рядов с положительными членами:

$sum{n=1}{infty}{u_n},~{u_n}$

$sum{n=1}{infty}{v_n},~{v_n}$

≤
Если $sum{n=1}{infty}{v_n}$ сходится, то $sum{n=1}{infty}{u_n}$ сходится;
если $sum{n=1}{infty}{u_n}$ расходится, то $sum{n=1}{infty}{v_n}$ расходится.
$lim{n{right}infty}{{u_n}/{v_n}}=k,$ v_n ≠ 0, 0 < k < ∞.
Либо и $sum{n=1}{infty}{u_n}$ , и $sum{n=1}{infty}{v_n}$ сходятся,
либо и $sum{n=1}{infty}{u_n}$ , и $sum{n=1}{infty}{v_n}$ расходятся.

Достаточные признаки сходимости числовых рядов с положительными членами

u_n

Признак Даламбера
Если существует $lim{n{right}infty}{{u_{n+1}}/{u_n}}=l$ , то $sum{n=1}{infty}{u_n}$ : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
Признак Коши
Если существует $lim{n{right}infty}{root{n}{u_n}}=l$ , то $sum{n=1}{infty}{u_n}$ : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
Интегральный признак сходимости
1) u_n > 0; 2) u_n ≥ u_n+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = u_n.
Либо и $sum{n=1}{infty}{u_n}$ , и сходятся,
либо и $sum{n=1}{infty}{u_n}$ , и расходятся.

Примеры числовых рядов

$sum{n=1}{infty}{1/{n_a}}$ : сходится, если a > 1; расходится, если a ≤ 1.
$sum{n=1}{infty}{{a^n}/n}$ : сходится, если a < 1; расходится, если a ≥ 1.
: сходится.
$sum{n=0}{infty}{aq^n}=a/{1-q}$ : сходятся, |q| < 1; расходятся, |q| ≥ 1.
: сходится;
$sum{n=1}{infty}{1/{{n}ln^{a}{n}}}$ : сходится, если a > 1; расходится, если a ≤ 1.
$sum{n=1}{infty}{1/{2^{n}{n}}}=ln{2}.$
$sum{n=1}{infty}{{(-1)^{n-1}}/n}=ln{2}$ : сходится условно.
$sum{n=1}{infty}{{(-1)^{n-1}}/{n^2}}={{pi}^2}/12$ : сходится абсолютно.
$sum{n=1}{infty}{{(-1)^{n}}/{n{!}}}=1/e$ : сходится абсолютно.

Функциональные ряды

Функциональный ряд – сумма вида $sum{n=1}{infty}{f_n(x)},~f_n(x),~n~{in}~N,~x~{in}~D.$

При $x=x_0~{in}~D$ из функционального ряда получается числовой ряд $sum{n=1}{infty}{f_n(x_0)}.$

Если для $x_0~{in}~D$ числовой ряд сходится, то точка x_0 называется точкой сходимости функционального ряда. Если в каждой точке $x~{in}~D_1~{subset}~D$ числовые ряды сходятся, то функциональный ряд называется сходящимся в области D_1 . Совокупность всех точек сходимости образует область сходимости функционального ряда.

$S_k(x)=sum{n=1}{k}{f_n(x)}$ – частичные суммы ряда. Функциональный ряд сходится к функции f(x), если $lim{k{right}{infty}}{S_k(x)}=f(x).$

Равномерная сходимость

Функциональный ряд, сходящийся для всех $x~{in}~D_1~{subset}~D_1$ из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер N(ε), такой, что при n > N(ε) выполняется неравенство R_n(x) < ε для всех x из области сходимости, где $R_n(x)=sum{k=n+1}{infty}{f_k(x)}$ — остаток ряда.

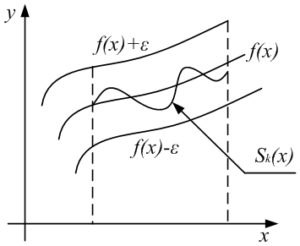
Геометрический смысл равномерной сходимости:

если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм S_k(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).

$sum{n=1}{infty}{f_n(x)}$ — называется мажорируемым в области , если существует такой сходящийся числовой ряд $sum{n=1}{infty}{u_n},$ u_n > 0, что для ∀x ∈ D f_n(x) ≤ u_n, n = 1, 2, …. Ряд $sum{n=1}{infty}{u_n}$ называется мажорантой ряда $sum{n=1}{infty}{f_n(x)}.$

Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Степенные ряды:
$sum{n=0}{infty}{a_n(x-x_0)^n}$ — степенной ряд по степеням x-x_0.
При $x_0=0~sum{n=0}{infty}{{a_n}{x^n}}$ – степенной ряд по степеням x.

Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
$R=1/{lim{n{right}{infty}}{delim{|}{{a_{n+1}}/{a_n}}{|}}}={lim{n{right}{infty}}{delim{|}{{a_n}/{a_{n+1}}}{|}}}$ или $R=1/{lim{n{right}{infty}}{root{n}{delim{|}{a_n}{|}}}}$
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.

На интервале сходимости ряд $sum{n=0}{infty}{{a_n}x^n}$ сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.

Свойства степенных рядов

Степенной ряд $sum{n=0}{infty}{{a_n}x^n}$ сходится равномерно на [−R′, R′]
∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости.
${(sum{n=0}{infty}{{a_n}x^n})}{prime}=sum{n=0}{infty}{{a_n}{(x^n)_x}{prime}},$ $int{}{}{(sum{n=0}{infty}{{a_n}x^n})dx}=sum{n=0}{infty}{a_n}int{}{}{x^n{dx}}.$
Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.

Разложение элементарных функций в степенные ряды

$f(x)=sum{n=0}{infty}{{a_n}x^n}=f(0)+{{f{prime}(0)}/{1{!}}}*x+{{f^{n}(0)}/{n{!}}}*x^n+{cdots}$

$e^x=1+x+{x^2}/{2{!}}+{cdots}=sum{n=0}{infty}{{x^n}/{n{!}}}$ , x ∈ (−∞; ∞).
$sh{x}={e^x-e^{-x}}/2=x+{x^3}/{3{!}}+{x^5}/{5{!}}+{cdots}+{x^{2n+1}}/{(2n+1){!}}+{cdots}=sum{n=0}{infty}{{x^{2n+1}}/{(2n+1){!}}}$ ,
x ∈ (−∞; ∞).
$ch{x}={e^x+e^{-x}}/2=1+{x^2}/{2{!}}+{cdots}+{x^{2n}}/{(2n){!}}+{cdots}=sum{n=0}{infty}{{x^{2n}}/{(2n){!}}}$ , x ∈ (−∞; ∞).
$sin{x}=x-{x^3}/{3{!}}+{x^5}/{5{!}}-{cdots}=sum{n=0}{infty}{{(-1)^n}*{{x^{2n+1}}/{(2n+1){!}}}}$ , x ∈ (−∞; ∞).
$cos{x}=1-{x^2}/{2{!}}+{x^4}/{4{!}}-{x^6}/{6{!}}+{cdots}=sum{n=0}{infty}{{(-1)^n}*{{x^{2n}}/{(2n){!}}}}$ , x ∈ (−∞; ∞).
$ln(1+x)=x-{x^2}/{2{!}}+{x^3}/{3{!}}-{x^4}/{4{!}}+{cdots}=sum{n=0}{infty}{{{{(-1)^{n-1}}/{n+1}}}*x^{n+1}}=$
${}=sum{n=1}{infty}{{{{(-1)^{n-1}}/{n}}}*x^{n}}$ , x ∈ (−1; 1].
$ln(1-x)=-x-{x^2}/{2{!}}-{x^3}/{3{!}}-{x^4}/{4{!}}+{cdots}={-}sum{n=0}{infty}{{{{x^{n+1}}/{n+1}}}}=$
${}={-}sum{n=1}{infty}{{{{x^{n}}/{n}}}}$ , x ∈ [−1; 1).
$ln({1+x}/{1-x})=2*(x+{x^3}/3+{x^5}/5+{x^7}/7+{cdots})=2*sum{n=0}{infty}{{{{x^{2n+1}}/{2n+1}}}}$ ,
x ∈ (−1; 1).
$arcsin{x}=x+sum{n=1}{infty}{{{1*3*5{cdots}(2n-1)}/{2*4*6{cdots}(2n-1)}}*{{{x^{2n+1}}/{2n+1}}}}$ , x ∈ [−1; 1].
$arctg{x}=x-{x^3}/{3}+{x^5}/{5}-{cdots}=sum{n=1}{infty}{{(-1)^{n-1}}*{{x^{2n-1}}/{2n-1}}}$ , x ∈ [−1; 1].
$(1+x)^m=1+sum{n=1}{infty}{{{m*(m-1){cdots}(m-n+1)}/{n{!}}}*x^n}$ , x ∈ (−1; 1).
$1/{1+x}=1-x+x^2-x^3+{cdots}=sum{n=0}{infty}{(-1)^n*x^n}$ , x ∈ (−1; 1).
$1/{1-x}=1+x+x^2+x^3+{cdots}=sum{n=0}{infty}{x^n}$ , x ∈ (−1; 1).
$sqrt{1+x}=1+{1/2}*x-{1/{2*4}}*x^2+{{1*3}/{2*4*6}}*x^3-{cdots}$ , x ∈ (−1; 1).
$1/{sqrt{1+x}}=1-{1/2}*x+{{1*3}/{2*4}}*x^2-{{1*3*5}/{2*4*6}}*x^3+{cdots}$ , x ∈ (−1; 1].

Тригонометрические ряды

Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):
$f(x)={{a_0}/2}+sum{n=1}{infty}{({a_n}*cos{{n*{pi}}/l}*x+{b_n}*sin{{n*{pi}}/l}*x)},$
где $a_0={1/l}*int{-l}{l}{f(x)dx},$ $a_n={1/l}*int{-l}{l}{f(x)cos{{n*{pi}}/l}*xdx},$ $b_n={1/l}*int{-l}{l}{f(x)sin{{n*{pi}}/l}*xdx},$

Разложение в ряд Фурье непериодических функций, заданных на отрезке

или на отрезке

${varphi}(x)=delim{[}{matrix{2}{1}{{f(x),~x{in}delim{[}{0;~l}{]}~} {{f_1}(x),~x{in}delim{[}{-l;~0}{]}~}}}{},~{f_1}(x)$

f₁(x)=f(-x), x ∈ [-l; 0] (четное продолжение)
$f(x)={{a_0}/2}+sum{n=1}{infty}{{a_n}*cos{{n*{pi}*x}/l}},$
где $a_n={2/l}*int{0}{l}{f(x)cos{{n*{pi}*x}/l}~dx},$ x ∈ [0; l] n = 0, 1, 2,…
f₁(x) = —f(−x), x ∈ [-l; 0]
(нечетное продолжение)
$f(x)=sum{n=1}{infty}{{b_n}*sin{{n*{pi}*x}/l}},$
где $b_n={2/l}*int{0}{l}{f(x)sin{{n*{pi}*x}/l}~dx},$ x ∈ [0; l] n = 1, 2,…
На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
– левый предел f(x) в точке x = l,
– правый предел f(x) в точке x = l.

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

dark_ai

Заголовок сообщения: Найти сумму ряда с синусом и дробью

Добавлено: 21 май 2012, 23:06

Начинающий

Зарегистрирован:
13 окт 2011, 00:20
Сообщений: 21
Cпасибо сказано: 4
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Надо найти сумму ряда с синусом и дробью

[math]sumlimits_{n=1}^{infty}3^nsinfrac{x}{3^n}[/math],

как это сделать?

Вернуться к началу

Human	Заголовок сообщения: Re: Сумма ряда Добавлено: 22 май 2012, 00:24
	Avgust писал(а): Синус при любом аргументе не выходит за свои узкие рамки. Если x не равен нулю, то все определяет 3^n. Не совсем понял Ваши рассуждения. Например, ряд [math]sum_{n=1}^{infty}2^nsinfrac x{3^n}[/math] сходится при всех [math]x[/math].
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Найти сумму ряда используя разложения ряда Фурье в форуме Ряды Фурье и Интегральные преобразования	Koleso	0	656	11 май 2017, 19:16
Найти сумму ряда с помощью ряда Фурье в форуме Ряды Фурье и Интегральные преобразования	Rempi Izek	4	1961	19 фев 2014, 21:01
Найти сумму ряда с помощью ряда Фурье в форуме Ряды Фурье и Интегральные преобразования	ka9aje	1	612	01 апр 2020, 15:44
Найти сумму ряда с помощью ряда Фурье в форуме Ряды	chillnory	1	214	16 апр 2020, 17:17
Исследовать сходимость ряда с синусом в форуме Ряды	Lina_Vls	1	767	13 апр 2014, 10:20
Сходимость ряда с синусом в знаменателе в форуме Ряды	arty1995	11	173	20 июн 2022, 09:04
Найти сумму ряда в форуме Ряды	tanyhaftv	4	754	20 янв 2021, 13:46
Найти сумму ряда в форуме Ряды	limao	1	912	29 май 2021, 10:31
Найти сумму ряда в форуме Ряды	Valter017	7	563	24 апр 2018, 21:11
Найти сумму ряда в форуме Ряды	albatroskuku	8	249	02 дек 2022, 22:37

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group

Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru

Русская поддержка phpBB

Источник

Числовые ряды

Функциональные ряды

Равномерная сходимость

Тригонометрические ряды

Кто сейчас на конференции

Не пропустите также: