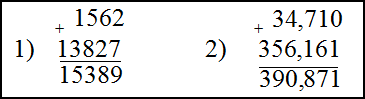Как найти сумму разных чисел - AvtoShod.ru - решение различных проблем

Содержание:

Определение суммы чисел
Свойства суммы чисел

Определение суммы чисел

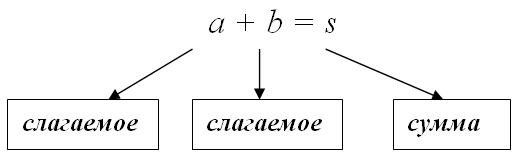
Суммой $s$ (лат. summa — итог, общее количество) чисел $a_{1}, a_{2}, dots, a_{n}$ называется результат
суммирования этих чисел: $s=a_{1}+a_{2}+ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то

Пример

Задание. Найти сумму чисел:

1) $12$ и $15$      2) $1,1 ; 2,2 ; 3,3$ и $4,4$

Ответ.

$12+15=27$

$1,1+2,2+3,3+4,4=11$

Свойства суммы чисел

Коммутативность: $n+m=m+n$

Ассоциативность: $(n+m)+k=n+(m+k)$

На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.

Дистрибутивность по отношению к умножению

$$(n+m) cdot k=n cdot k+m cdot k$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти сумму чисел удобным способом:

1) $15+17+13$   ;   2) $34+22+16+18$

Решение. По свойствам сложения имеем

$$15+17+13 =15+(17+13)=15+30=45 $$

$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$

Ответ. 1) $15+17+13=45$

            2) $34+22+16+18=90$

При сложении больших чисел или
десятичных дробей используется сложение в столбик.

Пример

Задание. Найти сумму чисел удобным способом:

1) $1562+13827$   ;   2) $34,71+356,161$

Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом.
В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем
числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном
столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:

Ответ. 1) $1562+13827=15389$

            2) $34,71+356,161=390,871$

Сложение рациональных дробей производится по правилу

$$frac{m}{n}+frac{p}{q}=frac{m cdot q+n cdot p}{n cdot q}$$

Пример

Задание. Найти сумму чисел:

1) $frac{1}{4}+frac{1}{6}$   ;   2) $frac{2}{3}+1 frac{1}{2}$

Решение. Вычислим первую сумму используя правило сложения рациональных чисел

$$frac{1}{4}+frac{1}{6}=frac{1 cdot 6+1 cdot 4}{4 cdot 6}=frac{6+4}{24}=frac{10}{24}$$

Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим

$$frac{1}{4}+frac{1}{6}=frac{5}{12}$$

Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого
умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим
правило сложение рациональных дробей

$$frac{2}{3}+1 frac{1}{2}=frac{2}{3}+frac{3}{2}=frac{2 cdot 2+3 cdot 3}{3 cdot 2}=frac{4+9}{6}=frac{13}{6}$$

Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком.
Полученное частное запишем в целую часть, а остаток от деления в числитель.

$$frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$$

Ответ. 1) $frac{1}{4}+frac{1}{6}=frac{5}{12}$   ;
2) $frac{2}{3}+1 frac{1}{2}=2 frac{1}{6}$

Читать дальше: что такое произведение чисел.

Источник

Калькуляторы

Найти сумму натуральных чисел от 1 до n
Найти сумму натуральных чисел от M до N
Возведение в степень
Теореме Пифагора
Калькулятор Фибоначчи
Найти углы треугольника
Найти углы прямоугольного треугольника
Углы равнобедренного треугольника
Углы ромба
Углы параллелограмма
Кубический корень
Извлечение корня из числа
Квадратный корень
Факториал числа
Радиус круга
Радиус цилиндра
Радиус шара
Радиус вписанной окружности в правильный многоугольник
Радиус окружности вписанной в треугольник
Радиус окружности описанной вокруг треугольника
Радиус вписанной и описанной окружности правильного треугольника
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной и описанной окружности равнобедренного треугольника
Теорема косинусов
Теорема синусов
Найти количество делителей числа
Количество сторон многоугольника
Число перестановок

Главная страница / Математические калькуляторы / Найти сумму натуральных чисел от M до N

Добавить в закладки

Введите число M

Введите число N

Знаков после запятой

Результат

Оставить комментарий (0)

(5 Оценок, Среднее: 4,40 из 5)

Loading…

Поделиться в социальных сетях:

или https://correctcalc.ru/matematicheskie-kalkulyatory/summa-chisel-ot-m-do-n/ скопировать ссылку на страницу

Онлайн-калькулятор поможет вычислить сумму числа от М до n, определить сумму числа на промежутках от одного числа до другого, вычислить сумму числа рядом натуральных числ в указанных интервалах. Чтобы вычислить сумму от A до B, используем формулу: (а + b) * b — a * 1 / 2 * a – наименьший ряд; b – наибольший ряд. Найти натуральную сумму от М до n. Введите количество М.

0 Комментариев |

; ; ; ; ;

Войти yandex google

Наш сайт использует файлы cookie, чтобы улучшить работу сайта, повысить его эффективность и удобство. Продолжая использовать сайт correctcalc.ru, вы соглашаетесь на использование файлов cookie.

Проценты

Процент от числа Процент одного числа от другого Прибавить процент к числу Вычесть процент из числа На сколько процентов одно число меньше другого На сколько процентов одно число больше другого Найти 100 процентов Процентное изменение Процентное соотношение Умножение на процент Деление на процент Разница в процентах Исходное значение Обратный прцент Число по проценту Снижение процентов

Математические

Сумма чисел от 1 до N Сумма чисел от M до N Возведение в степень Найти количество делителей числа Теорема Пифагора Фибоначи Найти углы треугольника Найти углы прямоугольного треугольника Углы равнобедренного треугольника Углы ромба Углы параллелограмма Кубический корень Извлечение корня из числа Квадратный корень Факториал числа Радиус круга Радиус цилиндра Радиус шара Радиус вписанной окружности в правильный многоугольник Радиус окружности вписанной в треугольник Радиус окружности описанной вокруг треугольника Радиус вписанной и описанной окружности правильного треугольника Радиус вписанной окружности в прямоугольный треугольник Радиус вписанной и описанной окружности равнобедренного треугольника Теорема косинусов Теорема синусов Количество сторон многоугольника Число перестановок

Дроби

Сложение дробей Вычитание дробей Деление дробей Умножение дробей Калькулятор сокращения дробей Возведения дробей в степень Перевод дроби в десятичную дробь Десятичная дробь в обыкновенную Смешанная дробь в обыкновенную Обыкновенная дробь в смешанную Обыкновенные дроби в проценты Калькулятор для сравнения дробей

Формула площади

Площадь прямоугольника Площадь треугольника Площадь кольца через радиусы Площадь круга Площадь квадрата Площадь квадрата по диагонали Площадь трапеции Площадь прямоугольного треугольника Площадь равнобедренного треугольника Площадь равностороннего треугольника Площадь параллелограмма Площадь эллипса Площадь четырехугольника Площадь сектора круга Площадь сегмента круга Площадь шара Площадь куба Площадь цилиндра Площадь пирамиды Площадь параллелепипеда Площадь конуса Площадь усеченного конуса Площадь тетраэдра Площадь призмы Площадь правильного многоугольника Площадь сектора кольца

Формула объема

Oбъема куба Oбъема параллелепипеда Объем конуса Объем призмы Объем цилиндра Объем шара Объем пирамиды Объем октаэдра Объем тетраэдра Объем усеченной пирамиды Объем усеченного конуса Объем шарового слоя Объем шарового сектора Объем шарового сегмента

Формула диагонали

Диагональ прямоугольника Диагональ квадрата Диагональ куба Диагональ прямоугольного параллелепипеда Диагонали ромба Диагонали параллелограмма Диагонали трапеции

Формула периметра

Периметр квадрата Периметр параллелограмма Периметр прямоугольника Периметр ромба Периметр трапеции Периметр треугольника Периметр четырехугольника Длина дуги Длина окружности круга Длина хорды окружности Периметр полукруга через диаметр Периметр полукруга через радиус

Формула высоты

Высота трапеции Высота ромба Высота параллелограмма Высота пирамиды Высота цилиндра Высота равнобедренного треугольника Высота равностороннего треугольникаа Высота треугольника

Формула стороны

Сторона треугольника Стороны прямоугольного треугольника Стороны равнобедренного треугольника Стороны равностороннего треугольника Стороны квадрата Стороны прямоугольника Стороны ромба Стороны параллелограмма Ребро пирамиды Ребро куба Боковое ребро параллелепипеда

Рассчет веса

Калькулятор индекса массы тела (ИМТ) Калькулятор идеального веса Процент жира-сухой мышечной массы Сколько воды нужно выпивать в день? Расчет количества мяса для шашлыка Расчет дней, за которые Вы сможете похудеть

Рассчет размера вещей

Калькулятор размеров обуви Калькулятор размеров мужской одежды Калькулятор размеров женской одежды Калькулятор размеров детской одежды

Животные

Сколько лет кошке по человеческим меркам

IT-специалисту

Перевод между системами счисления

Автомобилистам

Калькулятор расхода топлива

Бизнес калькуляторы

Сумма прописью онлайн Калькулятор НДС онлайн Калькулятор НДФЛ Сложный процент

Калькулятор дат

Количество дней между датами Количество недель между датами Сколько осталось до 23 февраля Сколько осталось до Нового года

Источник

Download Article

An arithmetic sequence is a series of numbers in which each term increases by a constant amount. To sum the numbers in an arithmetic sequence, you can manually add up all of the numbers. This is impractical, however, when the sequence contains a large amount of numbers. Instead, you can quickly find the sum of any arithmetic sequence by multiplying the average of the first and last term by the number of terms in the sequence.

1
Make sure you have an arithmetic sequence. An arithmetic sequence is an ordered series of numbers, in which the change in numbers is constant.^[1] This method only works if your set of numbers is an arithmetic sequence.
- To determine whether you have an arithmetic sequence, find the difference between the first few and the last few numbers. Ensure that the difference is always the same.
- For example, the series 10, 15, 20, 25, 30 is an arithmetic sequence, because the difference between each term is constant (5).
2
Identify the number of terms in your sequence. Each number is a term. If there are only a few terms listed, you can count them. Otherwise, if you know the first term, last term, and common difference (the difference between each term) you can use a formula to find the number of terms. Let this number be represented by the variable .
- For example, if you are calculating the sum of the sequence 10, 15, 20, 25, 30, , since there are 5 terms in the sequence.
Advertisement
3

Identify the first and last terms in the sequence. You need to know both of these numbers in order to calculate the sum of the arithmetic sequence. Often the first numbers will be 1, but not always. Let the variable $a_{{1}}$ equal the first term in the sequence, and $a_{{n}}$ equal the last term in the sequence.

1
Set up the formula for finding the sum of an arithmetic sequence. The formula is $S_{{n}}=n({frac {a_{{1}}+a_{{n}}}{2}})$ , where $S_{{n}}$ equals the sum of the sequence.^[2]
- Note that this formula is indicating that the sum of the arithmetic sequence is equal to the average of the first and last term, multiplied by the number of terms.^[3]
2
3

Calculate the average of the first and second term. To do this, add the two numbers, and divide by 2.^[5]
4

Multiply the average by the number of terms in the series. This will give you the sum of the arithmetic sequence.^[6]

1

Find the sum of numbers between 1 and 500. Consider all consecutive integers.
2

Find the sum of the described arithmetic sequence. The first term in the sequence is 3. The last term in the sequence is 24. The common difference is 7.
3

Solve the following problem. Mara saves 5 dollars the first week of the year. For the rest of the year, she increases her weekly savings by 5 dollars every week. How much money does Mara save by the end of the year?

Add New Question

Question

How can I determine whether the sequence is arithmetic?

A sequence is arithmetic if there is a constant difference between any term and the terms immediately before and after it: for example, if each term is 7 more than the term before it.
Question

Why do I need to divide by 2?

You do this so that you can find the average of the two numbers. For example, if you were finding the average between 7, 12, and 8, you would add them up (27) and divide them by the number of values you have. In this case, you have three numbers, so you’d divide 27 by 3 to get an average of 9. In the case of the sum of an arithmetic sequence, you have two numbers that you are finding the average of, so you divide it by the amount of values you have, which is two.
Question

What is the sum of all integers from 1 to 50?

LyKaxandra Caimoy

Community Answer

You will find that 1 + 50 = 2 + 49 = 3 + 48 (and so on). Multiply the sum, which is 51, by half of the last term. You have the equation 51 × 25 = 1275. The sum is therefore 1275.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To find the sum of an arithmetic sequence, start by identifying the first and last number in the sequence. Then, add those numbers together and divide the sum by 2. Finally, multiply that number by the total number of terms in the sequence to find the sum. To see example problems, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 605,421 times.

Did this article help you?

Источник

Онлайн калькулятор поможет найти сумму чисел от M до N, определит сумму чисел на промежутке от N1 до N2, найти сумму ряда натуральных чисел в указанном интервале.

Для нахождения суммы чисел от А до Б используется формула: (a+b)×(b-a+1)/2
a — наименьшее число ряда;
b — наибольшее число ряда.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Загрузить PDF

Если вы готовитесь к тестированию или просто хотите научиться быстро складывать числа, запомните, как суммировать целые числа от 1 до . Так как вы собираетесь складывать целые числа, вам не придется беспокоиться о дробях (обыкновенных и десятичных). Просто решите, какой формулой воспользоваться. Затем подставьте данное целое число вместо и найдите ответ.

1
Определите арифметическую последовательность. Посмотрите на ряд чисел, которые вы хотите сложить. Чтобы воспользоваться формулой для суммирования целых чисел, убедитесь, что ряд чисел действительно является последовательностью, то есть каждое число возрастает на одну и ту же величину.^[1]
- Например, ряд чисел 5, 6, 7, 8, 9 представляет собой последовательность, как и ряд 17, 19, 21, 23, 25.
- Ряд чисел 5, 6, 9, 11, 14 не является последовательностью, потому что числа возрастают на разные величины.
2
3
Найдите количество складываемых целых чисел. Чтобы суммировать целые числа от начального числа до , необходимо найти общее количество складываемых чисел. Например, если вы хотите сложить целые числа от 1 до 200, общее количество чисел вычисляется так: 200+1 = 201.^[2]
- Например, если нужно найти сумму целых чисел от 1 до 12, количество чисел: 12+1 = 13.
4
Найдите сумму целых чисел между двумя целыми числами, которые в расчете не участвуют. В этом случае вычтите 1 из .^[3]
- Например, чтобы найти сумму целых чисел между 1 и 100, вычтите 1 из 100 и получите 99.
Реклама

1
2
3
4
Пользуйтесь представленными формулами, чтобы найти сумму. Когда вы подставили нужно число в формулу, умножьте его на себя, прибавьте 1, 2 или 4 (в зависимости от формулы), а затем разделите результат на 2 или 4. ^[7]
- Пример 1: 100*101/2 = 10100/2 = 5050.
- Пример 2 (с четными числами): 20*22/4 = 440/4 = 110.
Реклама