Sum of squares refers to the sum of the squares of the given numbers, i.e., it is the addition of squared numbers. The squared terms could be two terms, three terms, or “n” number of terms, the first “n” odd or even terms, a series of natural numbers or consecutive numbers, etc. In statistics, the value of the sum of squares tells the degree of dispersion in a dataset. For this, we need to first find the mean of the given data, then the variation of each data point from the mean, square them, and finally, add them. In algebra, we use the (a + b)2 identity to determine the sum of the squares of two numbers. The formula that determines the sum of the squares of the first “n” natural numbers is derived with the help of the sum of the squares of the first “n” natural numbers. We perform these fundamental arithmetic operations, which are necessary for both algebra and statistics. There are various methods to determine the sum of squares of given numbers.
Sum of Squares Formula
The sum of the square formula is appliable for two, three, and up to n terms which are explained below:
Sum of squares for two numbers
Let a and b be two real numbers, then the formula for the addition of squares of the two numbers is given as follows:
a2 + b2 = (a + b)2 − 2ab
Proof:
From the algebraic identities, we have,
(a + b)2 = a2 + 2ab + b2
Now, subtract 2ab on both sides.
(a + b)2 − 2ab = a2 + 2ab + b2 − 2ab
a2 + b2 = (a + b)2 − 2ab
Hence, proved.
Sum of squares for three numbers
Let a, b, and c be three real numbers, then the formula for the addition of squares of the three numbers is given as follows:
a2 + b2 + c2 = (a +b + c)2 − 2ab − 2bc − 2ca
Proof:
From the algebraic identities, we have,
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
By subtracting 2ab, 2bc, and 2ca on both sides, we get,
a2 + b2 + c2 = (a + b + c)2 − 2ab − 2bc − 2ca
Hence, proved
Sum of squares for “n” Natural Numbers
Natural numbers are also known as positive integers and include all the counting numbers, starting from 1 to infinity. If 1, 2, 3, 4,… n are n consecutive natural numbers, then the sum of squares of “n” consecutive natural numbers is represented by 12 + 22 + 32 +… + n2 and symbolically represented as Σn2.
The formula for the sum of squares of the first “n” natural numbers is given as follows:
∑n2 = [n(n+1)(2n+1)]/6
Sum of Squares of First “n” Even Numbers
The formula for the sum of squares of the first “n” even numbers, i.e., 22 + 42 + 62 +… + (2n)2 is given as follows:
∑(2n)2 = 22 + 42 + 62 +… + (2n)2
∑(2n)2 = [2n(n+1)(2n+1)]/3
Sum of Squares of First “n” Odd Numbers
The formula for the sum of squares of the first “n” odd numbers, i.e., 12 + 32 + 52 +… + (2n – 1)2, can be derived using the formulas for the sum of the squares of the first “2n” natural numbers and the sum of squares of the first “n” even numbers.
∑(2n-1)2 = 12 + 32 + 52 + … + (2n – 1)2
∑(2n-1)2 = [n(2n+1)(2n-1)]/3
Proof:
∑(2n –1)2 = [12 + 22 + 32 + … + (2n – 1)2 + (2n)2] – [22 + 42 + 62 + … + (2n)2]
Now, apply the formula for the addition of squares of “2n” natural numbers and “n” even natural numbers, and we get;
∑(2n–1)2 = 2n/6 (2n + 1)(4n + 1) – (2n/3) (n+1)(2n+1)
∑(2n–1)2 = n/3 [(2n+1)(4n+1)] – 2n/3 [(n+1)(2n+1)]
Now, take out the common terms.
∑(2n–1)2 = n/3 (2n+1) [4n + 1 – 2n – 2]
∑(2n–1)2 = [n(2n+1)(2n–1)]/3
Hence, proved.
Sum of Squares in Statistics
Sum of squares of n data points = ∑ni=0 (xi – x̄)2
∑ = represents sum
xi = each value in the set
x̄ = mean of the values
xi – x̄ = deviation from the mean value
(xi – x̄)2 = square of the deviation
n = number of terms in the series
In statistics, the value of the sum of squares tells the degree of dispersion in a dataset. It evaluates the variance of the data points from the mean and aids in a better understanding of the data. The large value of the sum of squares indicates that there is a high variation of the data points from the mean value, while the small value indicates that there is a low variation of the data from its mean. Follow the steps given below to find the total sum of squares in statistics.
- Step 1: Count the number of data points in the given dataset.
- Step 2: Now, calculate the mean of the given data.
- Step 3: Subtract each data point from the mean calculated in step 2.
- Step 4: Now, determine the square of the difference obtained in step 3.
- Step 5: Finally, add the squares that we have determined in step 4.
Solved Examples based on Sum of Squares
Example 1: Find the sum of the given series: 12 + 22 + 32 +…+ 552.
Solution:
To find the value of 12 + 22 + 32 +…+ 552.
From the sum of squares formula for n terms, we have
∑n2 = 12 + 22 + 32 +…+ n2 = [n(n+1)(2n+1)] / 6
Given, n = 55
= [55(55+1)(2×55+1)] / 6
= (55 × 56 × 111) / 6
= 56,980
Thus, the sum of the given series is 56,980.
Example 2: Find the value of (32 + 82), using the sum of squares formula.
Solution:
To find the value of 32 + 82
Given: a = 3 and b = 8.
From the sum of squares formula, we have
a2 + b2 = (a + b)2 − 2ab
⇒ 32 + 82 = (3 +
2 − 2(3)(8)
= 121 – 2(24)
= 121 − 48
= 73.
Hence, the value of (32 + 82) is 73.
Example 3: Find the sum of squares of the first 25 even natural numbers.
Solution:
To find the value of 22 + 42 + 62 +… + 482+ 502.
= 22( 12 + 22 + 32 +…+252)
From the sum of squares formula for n terms, we have
∑n2 = [n(n+1)(2n+1)]/6
Here, n = 25
22( 12 + 22 + 32 +…+252) = 4[25(25+1)(2(25)+1)/6]
= (2/3) × (25) × (26) × (51)
= 22,100
Hence, the sum of squares of the first 25 even natural numbers is 22,100.
Example 4: A dataset has points 2, 4, 13, 10, 12, and 7. Find the sum of squares for the given data.
Solution:
Given: We have 6 data points 2, 4, 13, 10, 12, and 7.
The sum of the given data points = 2 + 4 + 13 + 10 + 12 + 7 = 48.
The mean of the given data is given by,
Mean, x̄ = Sum / Number of data points
= 48 / 6
= 8
So, the sum of squares is given by,
∑ni=0 (xi – x̄)2 = (2 –
2 + (4 –
2 + (13 –
2 + (10 –
2 + (12 –
2 + (7 –
2
= (–6)2 + (–4)2 + (5)2 + (2)2 + (4)2 + (–1)2
= 36 + 16 + 25 + 4 + 14 + 1
= 96
Hence, the sum of squares for the given data is 96.
Example 5: Calculate the sum of the squares of 4, 9, and 11 using the sum of squares formula for three numbers.
Solution:
To find the value of 4, 9, and 11.
Given, a = 4, b = 9, and c = 11.
From the sum of squares formula, we have
a2 + b2 + c2 = (a + b +c)2 − 2ab − 2bc − 2ca
42 + 92 + 112 = (4 + 9 + 11)2 −(2×4×9) − (2×9×11) − (2×11×4)
= 576 − 72 − 198 − 88
= 218
Hence, the value of (42 + 92 + 112) is 218.
Example 6: Find the sum of squares of the first 10 odd numbers.
Solution:
The sum of squares of the first 10 odd numbers: 12 + 32 + 52 +… +172 + 192
We know that,
The sum of squares of first “n” Odd Numbers ∑(2n–1)2 = [n(2n+1)(2n–1)]/3
Here, n is 10.
= [10×(2×10 + 1)(2×10 – 1)]/3
= [10 × 21 × 19]/3
= 10 × 7 × 19 = 1,330
Hence, the value of the sum of squares of the first 10 odd numbers is 1330.
FAQs based on Sum of Squares
Question 1: What is the Sum of Squares Error?
Answer:
Sum of squares error, also known as the residual sum of squares, is the difference between the actual value and the predicted value of the data.
Question 2: What Is the Expansion of Sum of Squares Formula?
Answer:
a2 + b2 formula is known as the sum of squares formula in algebra and it is read as a square plus b square. Its expansion is expressed as a2 + b2 = (a + b)2 – 2ab.
Question 3: Write the Sum of Squares Formula used in Algebra.
Answer:
The sum of squares formula used in algebra are:
- a2 + b2 = (a + b)2 − 2ab
- a2 + b2 + c2 = (a +b + c)2 − 2ab − 2bc − 2ca
Question 4: Write the sum of squares of the first five even numbers.
Answer:
The sum of squares of the first five even numbers is given by:
∑(2n)2 = [2n(n+1)(2n+1)]/3
putting n = 5
∑(2×5)2 = [2×5×(5+1)×(2×5+1)]/3
= 220
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b)2 = a2 ± 2ab + b2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c)3, однако формулы сокращенного умножения для простого выражения как:
a2 + b2
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a2 + b2 = (a + ib) × (a — ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a2 + b2 = (a + b)2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f2 = a2 + b2 + c2 + d2,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Найдите сумму квадратов всех однозначных чисел
1.
Которые делятся на 2
2.
Которые не делятся на 2
3, чисел
Объясните пожалуйста.
На этой странице находится ответ на вопрос Найдите сумму квадратов всех однозначных чисел1?, из категории
Математика, соответствующий программе для 1 — 4 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Математика. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Содержание
- Сумма квадратов
- Решение формулы суммы квадратов двух чисел
- Сумма квадратов всех целых чисел
- Формулы сокращенного умножения
- Рассмотрим примеры работы калькулятора
- Разложение на квадраты
- Гипотенуза 5-мерного тетраэдра
- Заключение
- Представление чисел суммой двух квадратов и эллиптические кривые
- Вычеты
- Чуть-чуть про эллиптические кривые
- Квадратичные вычеты и невычеты
- Доказательство
- Причём здесь криптография?
Сумма квадратов
Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?
Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.
Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:
Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:
Рассмотрим, как эти рассуждения могут быть применены на практике.
Теперь используем данные условия:
Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.
Источник
Решение формулы суммы квадратов двух чисел
АННОТАЦИЯ
В настоящей статье нами впервые предложено решение формулы сокращенного произведения, которая может широко применена в решении различных математических задач, равенств и неравенств, а также для упрощения сложных алгебраических выражений, имеющих широкое практическое применение в науке и технике.
ABSTRACT
In this article, we first proposed a solution to the abbreviated product formula, which can be used in solving various mathematical problems, equalities and inequalities, as well as to simplify complex algebraic expressions that have wide practical applications in science and technology.
Ключевые слова: формулы сокращенного произведения, сумма квадратов двух чисел.
Keywords: formulas of short multiplication, sum of squares two numbers.
Известно, что при решении задач во всех разделах математики очень часто используют формулы сокращенного произведения (ФСУ) [1. 163-182, 2. 115, 3. 134]. Эти формулы удачно используются при упрощении сложных математических выражений, при решении алгебраических, тригонометрических уравнений, неравенств, геометрических задач, учебных и научных проблем различной сложности. Ниже приведены официально всем известные ФСУ в табличном виде, из учебников Алгебры для 7 класса:
Таблица 1.
Формулы сокращенного умножения
Формула
Название
(a+b) 2 =a 2 +2ab+b 2
Квадрат суммы двух чисел
(a-b) 2 =a 2 -2ab+b 2
Квадрат разности двух чисел
Square of difference
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Куб суммы двух чисел
(a-b) 3 =a 3 -3a 2 b+3ab 2 -b 3
Куб разности двух чисел
Cube of difference
a 3 +b 3 =(a+b)(a 2 -ab+b 2 )
Сумма кубов двух чисел
a 3 -b 3 =(a-b)(a 2 +ab+b 2 )
Разность кубов двух чисел
Difference of cubes
a 2 -b 2 =(a-b)(a+b)
Разность квадратов двух чисел
Difference of squares
a 2 +b 2 = ?
Сумма квадратов двух чисел (Примечание: не разлагающаяся на члены) [8]
Sum of squares (Note: not expands) [8,10]
Наглядно видно из таблицы 1, что приведенные в ней формулы 1, 2; 3, 4; 5, 6; 7, 8 являются формулами-парами, которые отличаются нежели только со знаками у отдельных членов в левой части равенства. Однако, решение для урувнения формулой a 2 +b 2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена 7. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» 10. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.
В настоящей статье нами впервые предложена конкретное решение для формулы (8), для разложения суммы квадратов двух чисел на многочлены. Она имеет решение следующего вида:
/Mamarakhmonov.files/image001.png)
Доказательство. Результат последовательного произведения многочленов в правой части формулы (8), должны равняться сумме квадратов двух чисел, в левой части равенства. Для этого применяем правила последовательного умножения для многочленов к выражениям в скобках, в правой части равенства:
Примечание. Члены с одинаковыми абсолютными значениями, но с различными знаками взаимно сокращаются, как показано ниже:
/Mamarakhmonov.files/image003.png)
/Mamarakhmonov.files/image004.png)
В результате упрощения получим результат сумму квадратов двух чисел, идентичный, что в левой части равенства a 2 +b 2 .
Конец доказательства.
Предложенная нами формула для суммы квадратов двух чисел (8) является инновационной, новой и имеет в дальнейшем практическое применение как в математике, информатике, ИТ, в точных науках в целом, так и в других отраслях науки и техники.
Список литературы
Источник
Сумма квадратов всех целых чисел
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
Существует множество формул для решения подобных выражений, и дело не ограничивается квадратами. При помощи формул легко подсчитать куб разности или сумму многочленов n-ной степени. Мы легко можем подсчитать даже выражение (a + b + c) 3 , однако формулы сокращенного умножения для простого выражения как:
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
a 2 + b 2 = (a + ib) × (a — ib),
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
- 5 и 0 = 25;
- 1 и 4 = 25;
- 8 и 1 = 64;
- 4 и 7 = 64.
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
f 2 = a 2 + b 2 + c 2 + d 2 ,
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Источник
Представление чисел суммой двух квадратов и эллиптические кривые
Пусть p — нечётное простое число. Довольно широко известно, что p представимо в виде суммы двух квадратов целых чисел p=a 2 +b 2 тогда и только тогда, когда p при делении на 4 даёт остаток 1: 5=1 2 +2 2 , 13=3 2 +2 2 , 17=1 2 +4 2 , . ; 3, 7, 11,… непредставимы. Куда менее известно, что a и b можно записать красивой формулой, имеющей непосредственное отношение к одной эллиптической кривой. Об этом результате 1907 года за авторством немца по фамилии Jacobsthal и о связанных вещах мы сегодня и поговорим.
Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a 2 +b 2 : квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).
Вычеты
Натуральных чисел бесконечно много. Бывает полезно объединять их в классы по каким-нибудь признакам. В частности, объединение по остатку от деления на какое-нибудь число n приводит к вычетам по модулю n: вычет x̅ — это класс всех чисел, которые при делении на n дают тот же остаток, что и x. Что эквивалентно, вычет x̅ состоит из всех чисел вида x+n∙k, где k целое. В рамках данного поста все вычеты будут по модулю p (того самого нечётного простого числа из введения). Естественно, различных вычетов столько же, сколько может быть остатков от деления на p, то есть ровно p. По сравнению с бесконечностью натуральных чисел переход к вычетам сильно сокращает число вариантов.
Операции над классами далеко не всегда имеют смысл. Например, попытка сложить класс простых чисел с классом составных чисел не очень осмысленна: мы умеем складывать только числа, а у суммы простого числа и составного числа не видно свойств, общих для класса. Хотя члены клуба тавтологии и могут сказать, что сложение класса простых чисел и класса составных чисел даёт класс чисел, раскладывающихся в сумму простого числа и составного числа.
Для вычетов, тем не менее, сложение, вычитание и умножение, «унаследованные» от натуральных чисел, дают другие вычеты. Например, 2̅+3̅=5̅: возьмём любое число с остатком 2, любое число с остатком 3, и их сумма обязательно даст остаток 5. Вообще говоря, произведение двух ненулевых вычетов по произвольному модулю может внезапно оказаться нулём, 2̅∙3̅=0̅ по модулю 6, что неприятно. Но в случае простого модуля, очевидно, такого не бывает, как говорят, нет делителей нуля. Кроме того, можно решить уравнение a̅∙x̅=b̅ (операция деления) для любых двух вычетов, кроме случая a̅=0̅, и результат будет однозначно определён. Однозначность следует из того, что произведение ненулевых вычетов ненулевое. Поскольку a̅≠0̅, то наибольший общий делитель a и p равен 1 (здесь тоже нужна простота p), расширенный алгоритм Евклида найдёт x и y такие, что a∙x+p∙y=1, откуда следует a̅∙x̅=1̅, а значит, a̅∙(b̅∙x̅)=b̅.
Важное следствие из отсутствия делителей нуля: ненулевой многочлен от одной переменной степени n не может иметь более n корней. (Это хорошо известно для обычных целых чисел, но при использовании операций над вычетами требует дополнительного обоснования: уравнение 3̅∙x̅=0̅ по модулю 6 имеет три решения 0̅, 2̅, 4̅.) Действительно, обычное деление «в столбик» показывает, что любой многочлен f(x) можно представить в виде f(x)=(x-с)g(x)+(некоторая константа), где многочлен g(x) имеет степень на единицу меньше; если c — это корень f(x), то константа равна нулю (подставим x=c); если c’ — другой корень f(x), то он будет корнем g(x) (здесь важно отсутствие делителей нуля), так что процесс можно продолжить. Если уже набралось n корней, то оставшийся g(x) будет константой, причём ненулевой (иначе f(x)=0) и больше корней не имеет.
Вычеты по простому модулю можно складывать, вычитать, умножать. На ненулевые вычеты можно делить. Все эти операции обладают обычными свойствами типа a̅∙b̅=b̅∙a̅. В умных книгах говорят, что вычеты по простому модулю образуют поле (а вычеты по составному модулю, где делить нельзя, а всё остальное такое же, — коммутативное кольцо). И не надо быть умной книгой, чтобы назвать это поле конечным. Поле вычетов — не единственное конечное поле, но другие конечные поля нам не понадобятся.
Чуть-чуть про эллиптические кривые
Эллиптическую кривую по модулю p (тому самому нечётному простому числу) можно рассматривать как набор решений уравнения y 2 =x 3 +a2x 2 +a4x+a6, где x, y и все a — вычеты (каждое решение называется одной точкой), плюс одна специальная точка O, не имеющая пары x, y. Правая часть уравнения не должна делиться на квадрат, иначе это будет не эллиптическая кривая: в уравнении типа y 2 =(x-1̅) 2 (x+2̅) можно переменную y заменить на z=y/(x-1̅) и получить зависимость второй степени, а не третьей.
Если p≠3, то вместо переменной x можно взять x+a2/3̅, избавившись от члена с x 2 .
Ясно, что раз x, y принадлежат конечному множеству, то число точек на эллиптической кривой тоже конечно. Сколько их? Это сложный в общем случае вопрос. Мы ограничимся кривыми вида y 2 =x 3 -k∙x. Для таких кривых полное доказательство можно уложить в один пост Хабра (хотя и довольно длинный).
Квадратичные вычеты и невычеты
Зададимся сначала более простым вопросом. Сколько решений есть у уравнения y 2 =c, где y, c — вычеты? Пример для p=7:
| y | 0̅ | 1̅ | 2̅ | 3̅ | 4̅ | 5̅ | 6̅ |
| y 2 | 0̅ | 1̅ | 4̅ | 2̅ | 2̅ | 4̅ | 1̅ |
Если c=0̅, то решение одно, y=0̅. Остальные значения y разбиваются на две половины, от 1̅ до вычета, соответствующего (p-1)/2, и от вычета, соответствующего (p+1)/2, до -1̅. Раз y 2 =(-y) 2 , вторая половина строки значений y 2 зеркально-симметрична первой половине. С другой стороны, в каждой половине повторений нет, поскольку иначе у уравнения было бы как минимум 4 решения, что невозможно для многочлена степени 2. Значит, есть (p-1)/2 вычетов c, для которых решений ровно 2, и столько же вычетов c, для которых решений нет совсем.
Ненулевые вычеты c, для которых есть решение, называются квадратичными вычетами. Вычеты c, для которых решения нет, называются квадратичными невычетами. Стоит отметить, что квадратичный невычет — это таки вычет, просто ему не повезло быть квадратичным. Символ Лежандра 

Вернёмся к эллиптическим кривым. Число вариантов y для фиксированного x мы знаем, общее число точек на кривой y 2 =x 3 -k∙x можно записать, просуммировав по всем x и не забыв про специальную точку: 
Теперь мы готовы предъявить обещанные формулы для компонентов разложения p в сумму двух квадратов. Теорема. Пусть g — любой квадратичный невычет. Если p при делении на 4 даёт остаток 1, то 
причём число в первой скобке целое нечётное, число во второй скобке целое чётное. Если же p при делении на 4 даёт остаток 3, то обе суммы в скобках нулевые (а значит, число точек на эллиптических кривых равно p+1).
Доказательство
Поскольку пост и без того длинный, доказательство убрано под спойлер. Его можно спокойно пропустить без ущерба для восприятия.
Если взять ненулевой вычет c и умножить его на все вычеты от 1̅ до p̅-1̅, все произведения будут ненулевыми и попарно различными (если c∙x=c∙y, то c∙(x-y)=0̅, что при ненулевом c может быть только если x=y), а значит, это будет просто какая-то перестановка всех вычетов от 1̅ до p̅-1̅. Следовательно, 1̅∙2̅∙. ∙(p̅-1̅)=(c∙1̅)∙(c∙2̅)∙. ∙(c∙(p̅-1̅))=c p-1 ∙1̅∙2̅∙. ∙(p̅-1̅) и c p-1 =1̅ для любого ненулевого вычета c. (Это было доказательство малой теоремы Ферма.)
Значит, многочлен x p-1 -1=(x (p-1)/2 -1)(x (p-1)/2 +1) имеет p-1 корней. Значит, каждая скобка имеет (p-1)/2 корней (максимально возможное количество для степени скобок). Каждый квадратичный вычет — корень первой скобки (если x=c 2 , то x (p-1)/2 =c p-1 =1̅), их (p-1)/2, значит, всем квадратичным невычетам остаётся вторая скобка. Итак, символ Лежандра от c принадлежит тому же вычету, что и c (p-1)/2 . (Это было доказательство критерия Эйлера).
Как следствие, получаем 
Является ли -1̅ квадратичным вычетом? Зависит от знака (-1) (p-1)/2 . Если p при делении на 4 даёт остаток 1, то (p-1)/2 чётно, (-1) (p-1)/2 =1, -1̅ — квадратичный вычет. Если p при делении на 4 даёт остаток 3, то всё наоборот и -1̅ — квадратичный невычет.
Простая часть теоремы: p даёт остаток 3 при делении на 4. Тогда в каждой скобке слагаемые с x и -x отличаются друг от друга умножением на символ Лежандра от -1̅, то есть противоположны по знаку и в сумме дают 0. Поскольку все слагаемые, кроме x=0̅, разбиваются на пары с нулевой суммой, а слагаемое с x=0̅, нулевое, вся сумма равна 0.
Если p даёт остаток 1 при делении на 4, то слагаемые с x и -x равны и их сумма четна. Значит, вся сумма также четна и числа в скобках действительно целые. Чётность/нечётность после деления пополам ненамного сложнее: в первой скобке теоремы есть три нулевых слагаемых, остальные слагаемые разбиваются на (p-3)/2 пар с суммой ±2 в каждой паре; при любом знаке при делении на 4 получается остаток 2, вся сумма при делении на 4 даёт остаток такой же, как p-3, то есть 2. После деления пополам получим нечётное число. Во второй скобке теоремы всего одно нулевое слагаемое и (p-1)/2 пар с ±2, итоговый остаток от деления на 4 получается 0, после деления пополам остаётся чётное число.
Пусть p при делении на 4 даёт остаток 1. Обозначим первую скобку теоремы через a, вторую через b. Мы уже знаем, что a и b целые.
Для доказательства посчитаем двумя способами следующую странную величину N: число пятёрок вычетов (x1, y1, x2, y2, t) таких, что выполнены сразу два уравнения: y1 2 =x1 3 -t∙x1 и y2 2 =x2 3 -t∙x2.
В первом способе сначала зафиксируем t и посчитаем число четвёрок из x, y, после чего сложим результаты для всех t. Ясно, что при фиксированном t пара (x1, y1) может быть любой неспециальной точкой кривой y 2 =x 3 -t∙x, вторая пара (x1, y1) — столь же любой неспециальной точкой той же кривой, а общее число таких пар равно квадрату числа неспециальных точек. (Собственно, поэтому мы и рассматриваем странную величину, она позволяет подобраться к a 2 и b 2 .) Если t=0, то уравнение y 2 =x 3 , как уже говорилось, не задаёт эллиптическую кривую и имеет столько же решений, сколько уравнение z 2 =x (где y=z∙x), то есть ровно p. При t=1 получается p+2a решений, при t=g — p+2b решений. Что насчёт остальных значений t?
Если y 2 =x 3 -t∙x и c — какой-то ненулевой вычет, то c 6 y 2 =c 6 x 3 -c 6 t∙x, что эквивалентно (c 3 y) 2 =(c 2 x) 3 -c 4 t∙(c 2 x). Иными словами, если (x,y) — решение уравнения с t, то (c 2 x,c 3 y) — решение уравнения с c 4 t, так что число решений с t и с c 4 t совпадает. Сколько есть разных ненулевых вычетов вида c 4 ? С одной стороны, не менее (p-1)/4: (p-1) значений c могут «склеиваться» в группы размером не более 4. С другой стороны, если (p-1)/4 — целое число, то все такие вычеты — корни многочлена x (p-1)/4 -1, так что их не может быть больше (p-1)/4. Значит, их ровно (p-1)/4.
Итак, (p-1)/4 кривых имеют p+2a неспециальных точек, ещё (p-1)/4 кривых имеют p+2b неспециальных точек. Это уже половина всего, что надо.
Если y 2 =x 3 -t∙x, то g 3 y 2 =(g∙x) 3 -(g 2 t)(g∙x). При фиксированном x число решений уравнения g 3 y 2 =. равно 2 — число решений уравнения y 2 =. . Значит, число неспециальных точек на кривой с t=g 2 (а следовательно, на (p-1)/4 подобных кривых) равно 2p-(p+2a)=p-2a. Аналогично число неспециальных точек на кривой с t=g 3 равно 2p-(p+2b)=p-2b.
Итак, первый способ вычисления даёт
Во втором способе вычисления N сначала зафиксируем x1 и x2 и посчитаем число троек t и y, после чего сложим результаты для всех пар x. При x1=x2=0̅ есть ровно p вариантов: оба y должны быть нулями, t может быть любым. При x1=0̅ и ненулевом x2 должно быть y1=0, y2 может быть любым, t вычисляется однозначно, получается снова p вариантов. Ситуация с нулевым x2 и ненулевым x1 симметрична. Наконец, пусть оба x ненулевые. Тогда t=x1 2 -(y1 2 /x1) и нужно посчитать число пар y с условием (x2/x1)y1 2 =y2 2 +x2(x1 2 -x2 2 ).
Если x1=x2, то уравнение превращается в условие совпадения квадратов y, и различных пар y получается 1+2(p-1): нулевая и по два варианта y2 для каждого ненулевого y1. Если x1=-x2, ситуация аналогичная, поскольку p даёт остаток 1 при делении на 4 и -1̅ — квадратичный вычет.
Если x2/x1 — квадратичный вычет, не равный ±1̅, то существует какое-то ненулевое c такое, что c 2 =x2/x1. Тогда (c 2 y1 2 -y2 2 )=(c∙y1-y2)(c∙y1+y2)=x2(x1 2 -x2 2 ), выражение c∙y1-y2 может быть любым ненулевым вычетом, по нему однозначно определяется c∙y1+y2 и, следовательно, y1 и y2. Итого p-1 вариантов.
Если x2/x1 — квадратичный невычет, то аналогично эллиптическим кривым число решений равно 2p минус число решений в случае квадратичного вычета, то есть 2p-(p-1)=p+1.
Суммируем. Есть один вариант с x1=x2=0, дающий p решений. Есть 2(p-1) вариантов, где один из x нулевой, а другой ненулевой, каждый из вариантов даёт p решений. Есть 2(p-1) вариантов с x2=±x1, каждый из которых даёт 2p-1 решений. Есть (p-1)((p-1)/2-2) вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный вычет, отличный от ±1̅, каждый из этих вариантов даёт p-1 решений. Наконец, остаётся (p-1) 2 /2 вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный невычет, в каждом из этих вариантов p+1 решений. Итого 
Сравнение двух выражений для N завершает доказательство.
Причём здесь криптография?
Вычислять a и b, подсчитывая p раз символы Лежандра, непрактично. Куда быстрее с этим справится алгоритм Cornacchia. Практическая польза — использовать формулу для a, b в обратную сторону: можно доказать, что разложение p=a 2 +b 2 единственно с точностью до перестановки a и b и смены знаков, так что нахождение a и b влечёт знание числа точек на кривых y 2 =x 3 -t∙x для любого ненулевого t, это будет p+1±2a и p+1±2b.
Знание числа точек на кривой важно для криптографии на этой кривой. На эллиптической кривой можно ввести операцию сложения точек (о чём слышали, наверное, все, кто хоть что-то знает о криптографии) со специальной точкой O в роли нуля. На основе операции сложения можно определить умножение на натуральное число: 2P=P+P, 3P=P+P+P и так далее. Так вот, можно доказать, что если n — порядок кривой, то nP=O для любой точки P. Зная n, c, d, можно решать уравнения вида x∙(cP)=dP полностью аналогично делению вычетов: расширенный алгоритм Евклида найдёт x, y такие, что c∙x+n∙y=1, откуда x∙(cP)+y∙(nP)=P, то есть x∙(cP)=P. При этом, если c, d неизвестны, а cP и dP заданы координатами, то эффективных методов деления в общем случае неизвестно.
Вычислить число точек на заданной кривой довольно сложно (полиномиальный алгоритм существует, но на практике довольно медленный). Чтобы построить кривую с какими-нибудь свойствами на число точек, можно пытаться взять случайные коэффициенты и вычислять число точек в цикле, пока не получится то, что надо, но придётся подождать. К счастью, есть другой способ.
Если нас устраивает простое число вида 4k+1 и кривая специального вида y 2 =x 3 -t∙x (в некотором смысле это одна и та же кривая при любом ненулевом t) с числом точек p+1±2a или p+1±2b, можно её и взять. Что насчёт других кривых?
Немного позднее, в 1911 году, уже другой автор von Schrutka получил аналогичный результат для кривых вида y 2 =x 3 -t, простых вида 6k+1, представления p=a 2 +3b 2 . Значит, найти число точек на кривой y 2 =x 3 -t опять же позволяет алгоритм Cornacchia.
Позднее, по мере развития теории эллиптических кривых, выяснилось, что если есть какое-то представление 4p=a’ 2 +d∙b’ 2 , где d натуральное, при делении на 4 даёт остаток 0 или 3, взаимно простое с p и не слишком большое, то можно эффективно (даже если p очень большое) построить кривую, которая будет иметь ровно p+1±a’ точек. Два наименьших значения d=3 и d=4 соответствуют кривым y 2 =x 3 -t и y 2 =x 3 -t∙x. Пример для d=163: 
При нечётном p≠163 это уравнение задаёт эллиптическую кривую. Если 4p представимо в виде a’ 2 +163b’ 2 с целыми a’, b’, то число точек на эллиптической кривой равно p+1±a’. Если нет, то p+1. К сожалению, доказательство использует «тяжёлую» теорию, поэтому здесь не будет даже намёков.
Обычно, впрочем, будут получаться радикалы. Например, для d=15: 
Источник

 2 − 2(3)(8)
2 − 2(3)(8)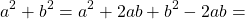
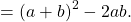
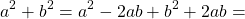
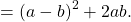
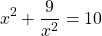



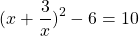
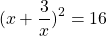
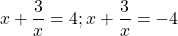
/Mamarakhmonov.files/image002.png)
/Mamarakhmonov.files/image005.png)