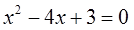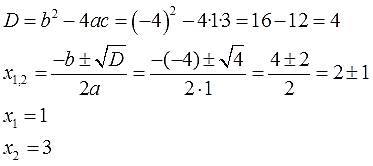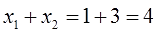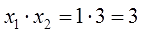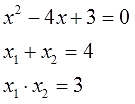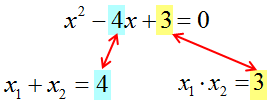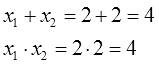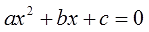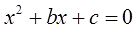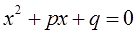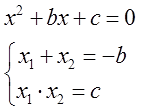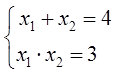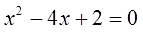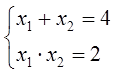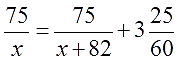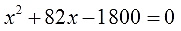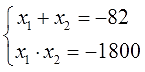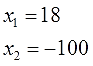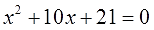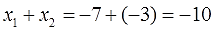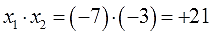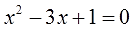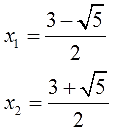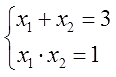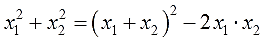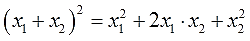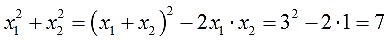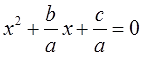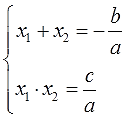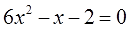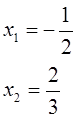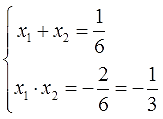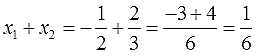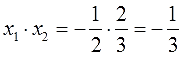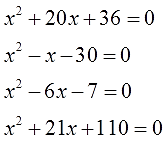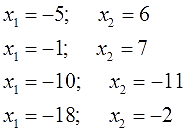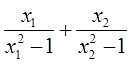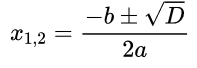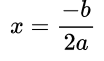Как найти сумму коэффициентов в квадратном уравнении - AvtoShod.ru

Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax 2 + c = 0, при b = 0;
ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

перенесем c в правую часть: ax 2 = — c,
разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b 2 −4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n 2 — ac;
если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Решение квадратных уравнений: формула корней, примеры

В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.

Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.

Квадратное уравнение, его виды

Квадратное уравнение – это уравнение, записанное как a · x 2 + b · x + c = 0 , где x – переменная, a , b и c – некоторые числа, при этом a не есть нуль.

Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.

Приведем пример для иллюстрации заданного определения: 9 · x 2 + 16 · x + 2 = 0 ; 7 , 5 · x 2 + 3 , 1 · x + 0 , 11 = 0 и т.п. – это квадратные уравнения.

Числа a , b и c – это коэффициенты квадратного уравнения a · x 2 + b · x + c = 0 , при этом коэффициент a носит название первого, или старшего, или коэффициента при x 2 , b – второго коэффициента, или коэффициента при x , а c называют свободным членом.

К примеру, в квадратном уравнении 6 · x 2 − 2 · x − 11 = 0 старший коэффициент равен 6 , второй коэффициент есть − 2 , а свободный член равен − 11 . Обратим внимание на тот факт, что, когда коэффициенты b и/или c являются отрицательными, то используется краткая форма записи вида 6 · x 2 − 2 · x − 11 = 0 , а не 6 · x 2 + ( − 2 ) · x + ( − 11 ) = 0 .

Уточним также такой аспект: если коэффициенты a и/или b равны 1 или − 1 , то явного участия в записи квадратного уравнения они могут не принимать, что объясняется особенностями записи указанных числовых коэффициентов. К примеру, в квадратном уравнении y 2 − y + 7 = 0 старший коэффициент равен 1 , а второй коэффициент есть − 1 .

Приведенные и неприведенные квадратные уравнения

По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.

Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен 1 . При иных значениях старшего коэффициента квадратное уравнение является неприведенным.

Приведем примеры: квадратные уравнения x 2 − 4 · x + 3 = 0 , x 2 − x − 4 5 = 0 являются приведенными, в каждом из которых старший коэффициент равен 1 .

9 · x 2 − x − 2 = 0 — неприведенное квадратное уравнение, где первый коэффициент отличен от 1 .

Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.

Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.

Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.

Решение

Cогласно указанной выше схеме разделим обе части исходного уравнения на старший коэффициент 6 . Тогда получим: ( 6 · x 2 + 18 · x − 7 ) : 3 = 0 : 3 , и это то же самое, что: ( 6 · x 2 ) : 3 + ( 18 · x ) : 3 − 7 : 3 = 0 и далее: ( 6 : 6 ) · x 2 + ( 18 : 6 ) · x − 7 : 6 = 0 . Отсюда: x 2 + 3 · x — 1 1 6 = 0 . Таким образом, получено уравнение, равносильное заданному.

Ответ: x 2 + 3 · x — 1 1 6 = 0 .

Полные и неполные квадратные уравнения

Обратимся к определению квадратного уравнения. В нем мы уточнили, что a ≠ 0 . Подобное условие необходимо, чтобы уравнение a · x 2 + b · x + c = 0 было именно квадратным, поскольку при a = 0 оно по сути преобразуется в линейное уравнение b · x + c = 0 .

В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.

Неполное квадратное уравнение – такое квадратное уравнение a · x 2 + b · x + c = 0 , где хотя бы один из коэффициентов b и c (или оба) равен нулю.

Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.

Порассуждаем, почему типам квадратных уравнений даны именно такие названия.

При b = 0 квадратное уравнение примет вид a · x 2 + 0 · x + c = 0 , что то же самое, что a · x 2 + c = 0 . При c = 0 квадратное уравнение записано как a · x 2 + b · x + 0 = 0 , что равносильно a · x 2 + b · x = 0 . При b = 0 и c = 0 уравнение примет вид a · x 2 = 0 . Уравнения, которые мы получили, отличны от полного квадратного уравнения тем, что в их левых частях не содержится либо слагаемого с переменной x , либо свободного члена, либо обоих сразу. Собственно, этот факт и задал название такому типу уравнений – неполное.

Например, x 2 + 3 · x + 4 = 0 и − 7 · x 2 − 2 · x + 1 , 3 = 0 – это полные квадратные уравнения; x 2 = 0 , − 5 · x 2 = 0 ; 11 · x 2 + 2 = 0 , − x 2 − 6 · x = 0 – неполные квадратные уравнения.

Решение неполных квадратных уравнений

Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:

a · x 2 = 0 , такому уравнению соответствуют коэффициенты b = 0 и c = 0 ;
a · x 2 + c = 0 при b = 0 ;
a · x 2 + b · x = 0 при c = 0 .

Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.

Решение уравнения a·x 2 =0

Как уже было указано выше, такому уравнению отвечают коэффициенты b и c , равные нулю. Уравнение a · x 2 = 0 возможно преобразовать в равносильное ему уравнение x 2 = 0 , которое мы получим, поделив обе части исходного уравнения на число a , не равное нулю. Очевидный факт, что корень уравнения x 2 = 0 это нуль, поскольку 0 2 = 0 . Иных корней это уравнение не имеет, что объяснимо свойствами степени: для любого числа p , не равного нулю, верно неравенство p 2 > 0 , из чего следует, что при p ≠ 0 равенство p 2 = 0 никогда не будет достигнуто.

Таким образом, для неполного квадратного уравнение a · x 2 = 0 существует единственный корень x = 0 .

Для примера решим неполное квадратное уравнение − 3 · x 2 = 0 . Ему равносильно уравнение x 2 = 0 , его единственным корнем является x = 0 , тогда и исходное уравнение имеет единственный корень — нуль.

Кратко решение оформляется так:

− 3 · x 2 = 0 , x 2 = 0 , x = 0 .

Решение уравнения a · x 2 + c = 0

На очереди — решение неполных квадратных уравнений, где b = 0 , c ≠ 0 , то есть уравнений вида a · x 2 + c = 0 . Преобразуем это уравнение, перенеся слагаемое из одной части уравнения в другую, сменив знак на противоположный и разделив обе части уравнения на число, не равное нулю:

переносим c в правую часть, что дает уравнение a · x 2 = − c ;
делим обе части уравнения на a , получаем в итоге x = — c a .

Наши преобразования являются равносильными, соответственно полученное уравнение также равносильно исходному, и этот факт дает возможность делать вывод о корнях уравнения. От того, каковы значения a и c зависит значение выражения — c a : оно может иметь знак минус (допустим, если a = 1 и c = 2 , тогда — c a = — 2 1 = — 2 ) или знак плюс (например, если a = − 2 и c = 6 , то — c a = — 6 — 2 = 3 ); оно не равно нулю, поскольку c ≠ 0 . Подробнее остановимся на ситуациях, когда — c a 0 и — c a > 0 .

В случае, когда — c a 0 , уравнение x 2 = — c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при — c a 0 ни для какого числа p равенство p 2 = — c a не может быть верным.

Все иначе, когда — c a > 0 : вспомним о квадратном корне, и станет очевидно, что корнем уравнения x 2 = — c a будет число — c a , поскольку — c a 2 = — c a . Нетрудно понять, что число — — c a — также корень уравнения x 2 = — c a : действительно, — — c a 2 = — c a .

Прочих корней уравнение не будет иметь. Мы можем это продемонстрировать, используя метод от противного. Для начала зададим обозначения найденных выше корней как _{x 1} и _{− x 1} . Выскажем предположение, что уравнение x 2 = — c a имеет также корень x 2 , который отличается от корней _{x 1} и _{− x 1} . Мы знаем, что, подставив в уравнение вместо x его корни, преобразуем уравнение в справедливое числовое равенство.

Для _{x 1} и _{− x 1} запишем: x 1 2 = — c a , а для x 2 — x 2 2 = — c a . Опираясь на свойства числовых равенств, почленно вычтем одно верное равенство из другого, что даст нам: x 1 2 − x 2 2 = 0 . Используем свойства действий с числами, чтобы переписать последнее равенство как ( x 1 − x 2 ) · ( x 1 + x 2 ) = 0 . Известно, что произведение двух чисел есть нуль тогда и только тогда, когда хотя бы одно из чисел является нулем. Из сказанного следует, что x 1 − x 2 = 0 и/или x 1 + x 2 = 0 , что то же самое, x 2 = x 1 и/или x 2 = − x 1 . Возникло очевидное противоречие, ведь вначале было условлено, что корень уравнения x 2 отличается от _{x 1} и _{− x 1} . Так, мы доказали, что уравнение не имеет иных корней, кроме x = — c a и x = — — c a .

Резюмируем все рассуждения выше.

Неполное квадратное уравнение a · x 2 + c = 0 равносильно уравнению x 2 = — c a , которое:

не будет иметь корней при — c a 0 ;
будет иметь два корня x = — c a и x = — — c a при — c a > 0 .

Приведем примеры решения уравнений a · x 2 + c = 0 .

Задано квадратное уравнение 9 · x 2 + 7 = 0 . Необходимо найти его решение.

Решение

Перенесем свободный член в правую часть уравнения, тогда уравнение примет вид 9 · x 2 = − 7 .
Разделим обе части полученного уравнения на 9 , придем к x 2 = — 7 9 . В правой части мы видим число со знаком минус, что означает: у заданного уравнения нет корней. Тогда и исходное неполное квадратное уравнение 9 · x 2 + 7 = 0 не будет иметь корней.

Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.

Необходимо решить уравнение − x 2 + 36 = 0 .

Решение

Перенесем 36 в правую часть: − x 2 = − 36 .
Разделим обе части на − 1 , получим x 2 = 36 . В правой части — положительное число, отсюда можно сделать вывод, что x = 36 или x = — 36 .
Извлечем корень и запишем окончательный итог: неполное квадратное уравнение − x 2 + 36 = 0 имеет два корня x = 6 или x = − 6 .

Ответ: x = 6 или x = − 6 .

Решение уравнения a·x 2 +b·x=0

Разберем третий вид неполных квадратных уравнений, когда c = 0 . Чтобы найти решение неполного квадратного уравнения a · x 2 + b · x = 0 , воспользуемся методом разложения на множители. Разложим на множители многочлен, который находится в левой части уравнения, вынеся за скобки общий множитель x . Этот шаг даст возможность преобразовать исходное неполное квадратное уравнение в равносильное ему x · ( a · x + b ) = 0 . А это уравнение, в свою очередь, равносильно совокупности уравнений x = 0 и a · x + b = 0 . Уравнение a · x + b = 0 линейное, и корень его: x = − b a .

Таким образом, неполное квадратное уравнение a · x 2 + b · x = 0 будет иметь два корня x = 0 и x = − b a .

Закрепим материал примером.

Необходимо найти решение уравнения 2 3 · x 2 — 2 2 7 · x = 0 .

Решение

Вынесем x за скобки и получим уравнение x · 2 3 · x — 2 2 7 = 0 . Это уравнение равносильно уравнениям x = 0 и 2 3 · x — 2 2 7 = 0 . Теперь следует решить полученное линейное уравнение: 2 3 · x = 2 2 7 , x = 2 2 7 2 3 .

Далее осуществим деление смешанного числа на обыкновенную дробь и определяем, что x = 3 3 7 . Таким образом, корни исходного уравнения это: x = 0 и x = 3 3 7 .

Кратко решение уравнения запишем так:

2 3 · x 2 — 2 2 7 · x = 0 x · 2 3 · x — 2 2 7 = 0

x = 0 или 2 3 · x — 2 2 7 = 0

x = 0 или x = 3 3 7

Ответ: x = 0 , x = 3 3 7 .

Дискриминант, формула корней квадратного уравнения

Для нахождения решения квадратных уравнений существует формула корней:

x = — b ± D 2 · a , где D = b 2 − 4 · a · c – так называемый дискриминант квадратного уравнения.

Запись x = — b ± D 2 · a по сути означает, что x 1 = — b + D 2 · a , x 2 = — b — D 2 · a .

Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.

Вывод формулы корней квадратного уравнения

Пускай перед нами стоит задача решить квадратное уравнение a · x 2 + b · x + c = 0 . Осуществим ряд равносильных преобразований:

разделим обе части уравнения на число a, отличное от нуля, получим приведенное квадратное уравнение: x 2 + b a · x + c a = 0 ;
выделим полный квадрат в левой части получившегося уравнения:
x 2 + b a · x + c a = x 2 + 2 · b 2 · a · x + b 2 · a 2 — b 2 · a 2 + c a = = x + b 2 · a 2 — b 2 · a 2 + c a
После этого уравнения примет вид: x + b 2 · a 2 — b 2 · a 2 + c a = 0 ;
теперь возможно сделать перенос двух последних слагаемых в правую часть, сменив знак на противоположный, после чего получаем: x + b 2 · a 2 = b 2 · a 2 — c a ;
наконец, преобразуем выражение, записанное в правой части последнего равенства:
b 2 · a 2 — c a = b 2 4 · a 2 — c a = b 2 4 · a 2 — 4 · a · c 4 · a 2 = b 2 — 4 · a · c 4 · a 2 .

Таким образом, мы пришли к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 , равносильному исходному уравнению a · x 2 + b · x + c = 0 .

Решение подобных уравнений мы разбирали в предыдущих пунктах (решение неполных квадратных уравнений). Уже полученный опыт дает возможность сделать вывод касательно корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 :

при b 2 — 4 · a · c 4 · a 2 0 уравнение не имеет действительных решений;
при b 2 — 4 · a · c 4 · a 2 = 0 уравнение имеет вид x + b 2 · a 2 = 0 , тогда x + b 2 · a = 0 .

Отсюда очевиден единственный корень x = — b 2 · a ;

при b 2 — 4 · a · c 4 · a 2 > 0 верным будет: x + b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = b 2 · a — b 2 — 4 · a · c 4 · a 2 , что то же самое, что x + — b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = — b 2 · a — b 2 — 4 · a · c 4 · a 2 , т.е. уравнение имеет два корня.

Возможно сделать вывод, что наличие или отсутствие корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 (а значит и исходного уравнения) зависит от знака выражения b 2 — 4 · a · c 4 · a 2 , записанного в правой части. А знак этого выражения задается знаком числителя, (знаменатель 4 · a 2 всегда будет положителен), то есть, знаком выражения b 2 − 4 · a · c . Этому выражению b 2 − 4 · a · c дано название — дискриминант квадратного уравнения и определена в качестве его обозначения буква D . Здесь можно записать суть дискриминанта – по его значению и знаку делают вывод, будет ли квадратное уравнение иметь действительные корни, и, если будет, то каково количество корней — один или два.

Вернемся к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 . Перепишем его, используя обозначение дискриминанта: x + b 2 · a 2 = D 4 · a 2 .

Вновь сформулируем выводы:

при D 0 уравнение не имеет действительных корней;
при D = 0 уравнение имеет единственный корень x = — b 2 · a ;
при D > 0 уравнение имеет два корня: x = — b 2 · a + D 4 · a 2 или x = — b 2 · a — D 4 · a 2 . Эти корни на основе свойства радикалов возможно записать в виде: x = — b 2 · a + D 2 · a или — b 2 · a — D 2 · a . А, когда раскроем модули и приведем дроби к общему знаменателю, получим: x = — b + D 2 · a , x = — b — D 2 · a .

Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:

x = — b + D 2 · a , x = — b — D 2 · a , дискриминант D вычисляется по формуле D = b 2 − 4 · a · c .

Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.

Алгоритм решения квадратных уравнений по формулам корней

Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.

В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.

Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.

Чтобы решить квадратное уравнение a · x 2 + b · x + c = 0 , необходимо:

по формуле D = b 2 − 4 · a · c найти значение дискриминанта;
при D 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
при D = 0 найти единственный корень уравнения по формуле x = — b 2 · a ;
при D > 0 определить два действительных корня квадратного уравнения по формуле x = — b ± D 2 · a .

Отметим, что, когда дискриминант есть нуль, можно использовать формулу x = — b ± D 2 · a , она даст тот же результат, что и формула x = — b 2 · a .

Примеры решения квадратных уравнений

Приведем решение примеров при различных значениях дискриминанта.

Необходимо найти корни уравнения x 2 + 2 · x − 6 = 0 .

Решение

Запишем числовые коэффициенты квадратного уравнения: a = 1 , b = 2 и c = − 6 . Далее действуем по алгоритму, т.е. приступим к вычислению дискриминанта, для чего подставим коэффициенты a , b и c в формулу дискриминанта: D = b 2 − 4 · a · c = 2 2 − 4 · 1 · ( − 6 ) = 4 + 24 = 28 .

Итак, мы получили D > 0 , а это означает, что исходное уравнение будет иметь два действительных корня.
Для их нахождения используем формулу корня x = — b ± D 2 · a и, подставив соответствующие значения, получим: x = — 2 ± 28 2 · 1 . Упростим полученное выражение, вынеся множитель за знак корня с последующим сокращением дроби:

x = — 2 + 2 · 7 2 или x = — 2 — 2 · 7 2

x = — 1 + 7 или x = — 1 — 7

Ответ: x = — 1 + 7 , x = — 1 — 7 .

Необходимо решить квадратное уравнение − 4 · x 2 + 28 · x − 49 = 0 .

Решение

Определим дискриминант: D = 28 2 − 4 · ( − 4 ) · ( − 49 ) = 784 − 784 = 0 . При таком значении дискриминанта исходное уравнение будет иметь лишь один корень, определяемый по формуле x = — b 2 · a .

x = — 28 2 · ( — 4 ) x = 3 , 5

Ответ: x = 3 , 5 .

Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0

Решение

Числовые коэффициенты этого уравнения будут: a = 5 , b = 6 и c = 2 . Используем эти значения для нахождения дискриминанта: D = b 2 − 4 · a · c = 6 2 − 4 · 5 · 2 = 36 − 40 = − 4 . Вычисленный дискриминант отрицателен, таким образом, исходное квадратное уравнение не имеет действительных корней.

В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:

x = — 6 + 2 · i 10 или x = — 6 — 2 · i 10 ,

x = — 3 5 + 1 5 · i или x = — 3 5 — 1 5 · i .

Ответ: действительные корни отсутствуют; комплексные корни следующие: — 3 5 + 1 5 · i , — 3 5 — 1 5 · i .

В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.

Формула корней для четных вторых коэффициентов

Формула корней x = — b ± D 2 · a ( D = b 2 − 4 · a · c ) дает возможность получить еще одну формулу, более компактную, позволяющую находить решения квадратных уравнений с четным коэффициентом при x (либо с коэффициентом вида 2 · n , к примеру, 2 · 3 или 14 · ln 5 = 2 · 7 · ln 5 ). Покажем, как выводится эта формула.

Пусть перед нами стоит задача найти решение квадратного уравнения a · x 2 + 2 · n · x + c = 0 . Действуем по алгоритму: определяем дискриминант D = ( 2 · n ) 2 − 4 · a · c = 4 · n 2 − 4 · a · c = 4 · ( n 2 − a · c ) , а затем используем формулу корней:

x = — 2 · n ± D 2 · a , x = — 2 · n ± 4 · n 2 — a · c 2 · a , x = — 2 · n ± 2 n 2 — a · c 2 · a , x = — n ± n 2 — a · c a .

Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:

x = — n ± D 1 a , где D 1 = n 2 − a · c .

Легко увидеть, что что D = 4 · D 1 , или D 1 = D 4 . Иначе говоря, D 1 – это четверть дискриминанта. Очевидно, что знак D 1 такой же, как знак D , а значит знак D 1 также может служить индикатором наличия или отсутствия корней квадратного уравнения.

Таким образом, чтобы найти решение квадратного уравнения со вторым коэффициентом 2 · n , необходимо:

найти D 1 = n 2 − a · c ;
при D 1 0 сделать вывод, что действительных корней нет;
при D 1 = 0 определить единственный корень уравнения по формуле x = — n a ;
при D 1 > 0 определить два действительных корня по формуле x = — n ± D 1 a .

Необходимо решить квадратное уравнение 5 · x 2 − 6 · x − 32 = 0 .

Решение

Второй коэффициент заданного уравнения можем представить как 2 · ( − 3 ) . Тогда перепишем заданное квадратное уравнение как 5 · x 2 + 2 · ( − 3 ) · x − 32 = 0 , где a = 5 , n = − 3 и c = − 32 .

Вычислим четвертую часть дискриминанта: D 1 = n 2 − a · c = ( − 3 ) 2 − 5 · ( − 32 ) = 9 + 160 = 169 . Полученное значение положительно, это означает, что уравнение имеет два действительных корня. Определим их по соответствующей формуле корней:

x = — n ± D 1 a , x = — — 3 ± 169 5 , x = 3 ± 13 5 ,

x = 3 + 13 5 или x = 3 — 13 5

x = 3 1 5 или x = — 2

Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.

Ответ: x = 3 1 5 или x = — 2 .

Упрощение вида квадратных уравнений

Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.

К примеру, квадратное уравнение 12 · x 2 − 4 · x − 7 = 0 явно удобнее для решения, чем 1200 · x 2 − 400 · x − 700 = 0 .

Чаще упрощение вида квадратного уравнения производится действиями умножения или деления его обеих частей на некое число. К примеру, выше мы показали упрощенную запись уравнения 1200 · x 2 − 400 · x − 700 = 0 , полученную делением обеих его частей на 100 .

Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Как пример используем квадратное уравнение 12 · x 2 − 42 · x + 48 = 0 . Определим НОД абсолютных величин его коэффициентов: НОД ( 12 , 42 , 48 ) = НОД(НОД ( 12 , 42 ) , 48 ) = НОД ( 6 , 48 ) = 6 . Произведем деление обеих частей исходного квадратного уравнения на 6 и получим равносильное ему квадратное уравнение 2 · x 2 − 7 · x + 8 = 0 .

Умножением обеих частей квадратного уравнения обычно избавляются от дробных коэффициентов. При этом умножают на наименьшее общее кратное знаменателей его коэффициентов. К примеру, если каждую часть квадратного уравнения 1 6 · x 2 + 2 3 · x — 3 = 0 перемножить с НОК ( 6 , 3 , 1 ) = 6 , то оно станет записано в более простом виде x 2 + 4 · x − 18 = 0 .

Напоследок отметим, что почти всегда избавляются от минуса при первом коэффициенте квадратного уравнения, изменяя знаки каждого члена уравнения, что достигается путем умножения (или деления) обеих частей на − 1 . К примеру, от квадратного уравнения − 2 · x 2 − 3 · x + 7 = 0 можно перейти к упрощенной его версии 2 · x 2 + 3 · x − 7 = 0 .

Связь между корнями и коэффициентами

Уже известная нам формула корней квадратных уравнений x = — b ± D 2 · a выражает корни уравнения через его числовые коэффициенты. Опираясь на данную формулу, мы имеем возможность задать другие зависимости между корнями и коэффициентами.

Самыми известными и применимыми являются формулы теоремы Виета:

x 1 + x 2 = — b a и x 2 = c a .

В частности, для приведенного квадратного уравнения сумма корней есть второй коэффициент с противоположным знаком, а произведение корней равно свободному члену. К примеру, по виду квадратного уравнения 3 · x 2 − 7 · x + 22 = 0 возможно сразу определить, что сумма его корней равна 7 3 , а произведение корней — 22 3 .

Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:

x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 — 2 · x 1 · x 2 = — b a 2 — 2 · c a = b 2 a 2 — 2 · c a = b 2 — 2 · a · c a 2 .

источники:

http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya

http://zaochnik.com/spravochnik/matematika/systems/reshenie-kvadratnyh-uravnenij/

Источник

Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax 2 + c = 0, при b = 0;
ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

перенесем c в правую часть: ax 2 = — c,
разделим обе части на a: x 2 = — c/а.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b 2 −4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

Формула корней для четных вторых коэффициентов

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

где D₁ = n 2 — ac.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n 2 — ac;
если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Обратная теорема Виета

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

«Решение квадратных уравнений с помощью свойств коэффициентов»
план-конспект занятия по алгебре (8 класс) на тему

Ознакомление еще с одним способом решения квадратных уравнений, который поможет быстро найти корни квадратного уравнения. Его можно назвать так: свойства коэффициентов квадратного уравнения.

Скачать:

Вложение	Размер
svoystva_koeffitsientov.doc	105.5 КБ

Предварительный просмотр:

Материал к уроку по теме «Решение квадратных уравнений с помощью свойств коэффициентов»

Тема: «Решение квадратных уравнений с помощью свойств коэффициентов»

Тип занятия: Изучение нового материала

Вид занятия: Урок углубления знаний

Возраст учащихся: 8 класс

Форма работы: индивидуальная, групповая

Оборудование: мультимедийный компьютер.

Познавательный
Частично-поисковый
Систематизирующий
Коммуникативный
Логический

Формирование знания и умения решения квадратных уравнений с помощью свойств коэффициентов

Познакомить с теорией способа решения квадратных уравнений с помощью свойств коэффициентов
Познакомить с применением способа решения квадратных уравнений с помощью свойств коэффициентов на практике
Сформировать умения составлять алгоритмы для данного способа решения квадратных уравнений
Развитие вычислительных навыков
Развитие кругозора учащихся

Развитие умения наблюдать, анализировать.
Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, познавательных интересов, творческих способностей учащихся.
Развитие коммуникативных качеств личности

Воспитание навыков сотрудничества в процессе совместной работы.

Содействовать воспитанию интереса к математике, активности, мобильности, отношения ответственной зависимости, взаимопомощи, умения общаться, толерантности у детей
Воспитание самостоятельности, умения представлять выбранный способ решения уравнения

Организационный момент. Вступительное слово учителя
Актуализация опорных теоретических и практических знаний о способах решения квадратных уравнений
Объяснение нового материала
Закрепление нового материала
Подведение итогов

Оформление доски: на доске написано

«Человеку, изучающему алгебру, часто полезно решить одну и ту же задачу тремя различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче, эффективнее. Так вырабатывается опыт». У.У. Сойер

Вступительное слово учителя. Сообщается цель, задачи занятия, план работы на занятии.

Актуализация опорных теоретических и практических знаний – повторение формул корней квадратных уравнений, алгоритмов известных способов решения квадратных уравнений.

С целью повторения и закрепления теоретических знаний проводится математический диктант. Продолжите предложение:

1. Уравнение вида ax 2 + bx + c = 0 называется.

2. Дискриминант находится по формуле D =.

3.Формула корней квадратного уравнения x =…

4. Если D > 0 , то квадратное уравнение имеет …

5. Если D , то уравнение …

6. Если D = 0 , то уравнение….

7. Уравнение вида x 2 + qx + p = 0 называется …

8. Уравнения вида ax 2 = 0, ax 2 + b x= 0, ax 2 + c = 0, где а ≠ 0, b ≠ 0, с ≠ 0 называются …

9.Если х 1 и х 2 – корни уравнения х 2 + рх + q = 0 , то справедливы формулы x 1 + x 2 =… и х 1 х 2 =…

Взаимопроверка (ответы проецируются на экран).

Работа в группах (учащиеся делятся на 3 группы, назначается руководитель группы, который помогает организовать работу группы).

На экран проецируются в произвольном порядке различные виды квадратных уравнений. I группа выписывает и решает уравнения вида ax 2 +bx+c=0. II группа – приведённые квадратные уравнения. III группа – неполные квадратные уравнения.

1) 2x 2 – 9x + 4 = 0 4) x 2 – 6x – 16 = 0 7) 10 + 3x-x 2 = 0

2) x 2 – 16x = 0 5) 9 – x 2 = 0 8x 2 + 8 = 0

3) 7x 2 +9x + 2 = 0 6) 3 – 5x – 2x 2 = 0 9) x 2 -5x-1 = 0

Руководители групп делегируют учеников поочередно к доске для решения уравнений.

Далее повторение следующих способов решения квадратных уравнений:

1. Способа разложения на множители

2. Способа выделения квадрата двучлена

3. Графического способа

К доске выходят по одному представителю от каждой группы, остальные учащиеся решают в тетради. I группа решает квадратное уравнение разложением левой части уравнения на множители, II группа – выделением квадрата двучлена, III группа – графическим способом.

Проверка проводится по группам учащихся с одинаковыми заданиями.

1) Способом разложения на множители:

7х 2 + 7х + 2х + 2 = 0

7х (х + 1) + 2(х +1) = 0

7х + 2 = 0 или х + 1 = 0

х = – 2/7 или х = – 1

2) Способом выделения квадрата двучлена:

3(х 2 + 2/3 х –5/3) = 0

х 2 + 2* 1/3 х + 1/9 – 1/9 – 5/3=0

х + 1/3 = 4/3 или х + 1/3 = –4/3

3) Графическим способом

у = х 2 , графиком является парабола

у = 2х + 3 , графиком является прямая

Прямая и парабола

имеют две общие точки,

абсциссы которых являются

Изучение нового материала. Ознакомление ещё с одним способом решения квадратных уравнений, который поможет быстро и, притом, устно найти корни уравнения. Его можно назвать так: свойства коэффициентов квадратного уравнения.

Рассмотрим несколько квадратных уравнений и найдём сумму коэффициентов.

5x 2 – 8x + 3 = 0 x 1 = 1 1 x 2 = 3 / 5 5 – 8 + 3 = 0

6x 2 – 7x + 1 = 0 x 1 = 1 1 x 2 = 1 / 6 6 – 7 + 1 = 0

2x 2 + 3x – 5 = 0 x 1 = 1 1 x 2 = 5 / 2 2 + 3 – 5 = 0

x 2 – 8x + 7 = 0 x 1 = 1 1 x 2 = 7 1 – 8 + 7 = 0

Какой вывод вы можете сделать?

Вывод : Если сумма коэффициентов квадратного уравнения равна 0, то:

1) один корень равен 1 ;

2) другой корень равен C / а .

Решите устно (уравнения спроецированы на экран).

1) x 2 + 23x – 24 = 0

2) 2x 2 + x – 3 = 0

3) x 2 + 15x – 16 = 0

4) 5x 2 + x – 6 = 0

5) 7x 2 – 9x + 2 = 0

6) 4x 2 – x – 3 = 0

7) 1999x 2 – 2000x + 1 = 0

839x 2 – 448x – 391 = 0

Проверка: представители групп записывают варианты своих ответов на доске.

Решим письменно на доске и в тетрадях 3 квадратных уравнения (по одному уравнению каждой группе) по формулам корней квадратных уравнений:

2) x 2 – 9x – 10 = 0

3) 5x 2 – 4x – 9 = 0

Попробуйте найти некую закономерность в корнях уравнений в соответствии с коэффициентами. Сделайте вывод.

Вывод: Если для коэффициентов выполняется равенство а – в + с = 0 , то один из корней уравнения равен –1 , а другой – с/а .

Решите устно уравнения (спроецированы на экран).

1) 11x 2 + 27x + 16 = 0

2) x 2 – 7x – 8 = 0

3) 9x 2 + 10x + 1 = 0

4) 6x 2 + 5x – 1 = 0

6) 939x 2 + 978х + 39 = 0

Проверка: Запись ответов на доске по группам.

Доказываем справедливость полученных выводов и записываем доказательство с примерами в справочной тетради.

Пусть дано квадратное уравнение

ах 2 + bх + с = 0, а ≠ 0.

1.Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1, х 2 = .

Доказательство . Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

Согласно теореме Виета

По условию а + b + с = 0, откуда b = – а – с . Значит,

Получаем х 1 = 1 , х 2 = , что и требовалось доказать.

2. Если а – b + с = 0, или b = а + с, то х 1 = – 1, х 2 = – .

Доказательство . По теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

т.е. х 1 = – 1 и х 2 = , что и требовалось доказать.

1. Решим уравнение 345х 2 – 137х – 208 = 0 .

Решение . Так как а + b + с = 0 (345 – 137 – 208 = 0) , то х 1 = 1, х 2 = = = –

2. Решим уравнение 132х 2 + 247х + 115 = 0

Решение. Так как а – b + с = 0 (132 – 247 + 115 = 0) , то х 1 = – 1, х 2 = –

5х 2 – 7х + 2 = 0 5) 839х 2 – 448х – 391 = 0
3х 2 + 5х – 8 = 0 6) 939х 2 + 978х +39 = 0
11х 2 + 25х – 36 = 0 7) 313х 2 + 326х + 13 = 0
11х 2 + 27х +16 = 0 2006х 2 – 2007х + 1 = 0

Подвести итоги занятия.

Учитель сообщает о том, что есть еще несколько способов решения квадратных уравнений, которые будут рассмотрены на следующих занятиях, рекомендует поискать их в математических книгах.

По теме: методические разработки, презентации и конспекты

№70-71 обобщающий урок по теме «Решение квадратных уравнений при помощи формул» 8 класс

Карточка плана-конспектаТема и номер урока в теме№ 70-71 обобщающий урок по теме «Решение квадратных уравнений при помощи формул»ПредметМатематикаКласс8Базовый учебникАлимов Ш. А. и др.

Комплексные числа. Лекция 2. Решение квадратных уравнений с действительными и комплексными коэффициентами.

Опорный конспект для студентов СПО технических специальностей по дисциплине «Математика». раздел 1. Алгебра.

конспект урока по алгебре 8 класс «Решение квадратных уравнений с четным вторым коэффициентом»

План конспект открытого урока по алгебре «Решение квадратных уравнений с четным вторым коэффициентом» в рамках ФГОС в 8 классе.

Урок алгебры в 8 классе по теме «Решение квадратных уравнений с помощью формул»

Урок изучения нового материала по алгебре в 8 классе по теме Решение квадратных уравнений с помощью формулы дискриминанта.

Методическая разработка урока алгебры в 8 классе по теме «Решение квадратных уравнений при помощи формул»

Данная методическая разработка представляет технологическую карту урока по алгебре в 8 классе. Урок построен на технологии проектного обучения. Даёт возможность учащимся активизировать свою поисковую .

Методические рекомендации к изучению темы: « Решение квадратных уравнений» с применением теоремы Виета для решения приведенного квадратного уравнения и полного квадратного уравнени

Решать квадратные уравнения учащимся приходится часто в старших классах, Решение иррациональных, показательных , логарифмических ,тригонометрических уравнений часто сводится к решени.

Презентация по теме «Решение квадратных уравнений с помощью переноса старшего коэффициента»

При решении квадратных уравнений удобно использовать теорему Виета. Но данную теорему проблематично использовать для решения не приведенных квадратных уравнений. Метод переноса старшего коэффициента п.

источники:

http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya

http://nsportal.ru/shkola/algebra/library/2015/03/29/reshenie-kvadratnyh-uravneniy-s-pomoshchyu-svoystv-koeffitsientov

Источник

Теорема Виета в квадратных уравнениях — штука простая и очень-очень важная. Позволяет делать массу полезных вещей буквально в уме. Имеет смысл познакомиться и освоить, правда? Тем более это совсем просто. Сомневаетесь? Напрасно.) Сами увидите. Читаем дальше.

Что такое приведённое квадратное уравнение? Складываем и перемножаем корни…

Знакомство наше начнём с безобидного уравнения:

Обычное квадратное уравнение, ничего выдающегося. Коэффициенты a, b и c здесь следующие:

a = 1; b = -4; c = 3

Решаем тоже как обычно, безо всяких фокусов, через дискриминант и получаем два корня:

Уравнение как уравнение — и что с того? Ничего, сейчас интересно будет!)

Первым делом я возьму корни нашего уравнения и… сложу их.) Зачем? Так надо!

Итак:

Теперь проделаю ещё одну бесполезную (казалось бы!) штуку. Перемножу корни:

Ну сложил, ну перемножил — и что? Спокойствие и терпение!

Выпишем ещё разок само уравнение, а прямо под ним напишем сумму и произведение корней:

И посмотрим на нашу запись. Внимательно посмотрим… Ничего не бросается в глаза? Ведь многие важные открытия в математике совершались на основе хорошей наблюдательности, между прочим! Не видите…

А вот так?)

Да! Сумма корней нашего квадратного уравнения равна коэффициенту b. Но, обратите внимание, не просто b, а с противоположным знаком! В уравнении коэффициент при икс (а это и есть буковка b) равен минус четыре. Сумма же корней даёт плюс четыре. То есть, –b.

А произведение корней даёт нам свободный член! Т.е. буковку c. Даёт со своим знаком! Как была в уравнении тройка (с=3), так в произведении корней тройкой же и осталась.)

Теперь я немного изменю уравнение. Поменяю в нём свободный член с тройки на четвёрку. Вот такое уравнение теперь решим:

Решаем точно так же, через дискриминант (здесь он равен нулю), и получаем единственное решение x=2.

Но мы с вами люди уже достаточно взрослые и понимаем, что это не один корень, а два одинаковых:

x_1,2= 2

Поэтому снова сосчитаем сумму и произведение корней:

И опять в сумме мы получили –b (-b=+4), а в произведении с (c=+4)!

А вот это уже крайне важно! Оказывается, такая забавная штука будет получаться всегда для любого квадратного уравнения! Если оно имеет корни, разумеется.) Правда, уравнения не какого попало, а такого, где квадрат икса чистый (т.е. коэффициент a=1). В математике такие квадратные уравнения имеют своё особое название — приведённые квадратные уравнения.

Запоминаем:

Квадратное уравнение, в котором коэффициент при х² равен единице (а=1), называется приведённым квадратным уравнением. Весьма важная штука!

Как оно выглядит в общем виде? Очень просто. Подставим в общий вид квадратного уравнения

единичку вместо а и получим общий вид приведённого квадратного уравнения:

В некоторых учебниках коэффициенты b и с переобозначают другими буквами (чаще всего p и q) и получают вот такой общий вид

Но суть та же самая. Как говорится, хоть горшком назови… Лично я предпочитаю использовать традиционные буквы b и с. Для универсальности.)

Ну и что из этого? — спросите вы. Чем приведённые квадратные уравнения так выделяются на фоне остальных квадратных, неприведённых? А дело вот в чём.

Что такое теорема Виета?

Итак, мы выяснили, что в приведённом квадратном уравнении (любом!) сумма коэффициентов равна –b, а произведение равно с. Всегда. Ясное дело, если дискриминант неотрицательный и корни у уравнения имеются.

Математически эта фишка записывается вот так:

Этот любопытный факт — и есть теорема Виета! Собственной персоной.

А словами она звучит вот как:

Теорема Виета:

Если ПРИВЕДЁННОЕ квадратное уравнение имеет корни, то их сумма равна коэффициенту при икс, взятому с противоположным знаком (—b), а их произведение равно свободному члену (c).

Вот и всё, никаких премудростей.)

Хотите строгое доказательство? Пожалуйста! Флаг вам в руки!) Распишите общую формулу корней квадратного уравнения для a=1, составьте сумму и произведение корней в общем виде. Т.е. через буквы. И упростите. Попробуйте! Весьма полезно и познавательно, между прочим.)

Верна также и обратная теорема:

Если числа х₁ и х₂ таковы, что их сумма равна –b, а произведение равно c, то эти числа являются корнями приведённого квадратного уравнения x² + bx + c = 0.

А по секрету скажу вам, что, на самом деле, именно обратной теоремой вы и пользуетесь, так умело подбирая в уме корни уравнения по сумме и произведению! Об этом подборе как раз дальше будет.)

Зачем нужна теорема Виета?

Полезная вещь первая — подбираем корни в уме!

Теорема Виета (обратная форма) позволяет искать корни многих квадратных уравнений гораздо быстрее и проще, чем традиционным путём через дискриминант. В буквальном смысле устно!

Вернёмся к нашему уравнению:

Теперь, вооружившись глубокими познаниями, прямо по теореме Виета, записываем системку для наших искомых корней:

Вопрос на сообразительность: какие же такие два числа в сумме дают четвёрку, а в произведении — тройку? Немного подумав головой, можно довольно быстро догадаться, что это чиселки 1 и 3.

Значит, можно смело записать:

x₁ = 1

x₂ = 3

Вот и всё. Это и будут корни нашего уравнения. Оба подходят.) Здорово, правда? И не нужно считать никаких дискриминантов, возиться с общей формулой корней. В которой, между прочим, можно и ошибок наляпать… Сразу, в уме, получен верный ответ!

Возможно, кто-то уже приготовил мне вопрос. Очень грамотный вопрос, кстати. А всегда ли в случае приведённого квадратного уравнения можно вот так красиво и легко подобрать корни?

К сожалению, нет. Далеко не всегда. Например, я снова изменю в исходном уравнении свободный член, только вместо четвёрки напишу двойку. Вот такое уравнение пусть будет:

Уравнение приведённое, коэффициент а равен единичке, вроде бы, всё нормально. Пишем теорему Виета:

И снова пробуем подобрать иксы так, чтобы оба равенства сработали!

Гм… Что-то не подбирается, правда? Какие бы целые числа вы бы ни подбирали, ничего не выйдет.

Тут выход только один — решать через дискриминант. Ибо дискриминант — штука универсальная. Спасает всегда — и в приведённых уравнениях, и в обычных. Попробуйте. И вы убедитесь, что корни этого уравнения получаются иррациональными. Естественно, такие корни подобрать в уме несколько затруднительно, да…

Догадываюсь, что вы сейчас спросите: Зачем же нам тогда городить огород, пробовать подобрать корни, если дискриминант всё равно надёжнее и с ним-то уж точно всё решится?

Да, надёжнее, но… Не всё так просто, как кажется!

Дело всё в том, что квадратные уравнения изучаются в 8-м классе, где народ тренируется на простых (иногда — совсем примитивных) задачках. И… привыкает к простоте.) Затем, в старших классах и особенно в институте, при изучении высшей математики, квадратные уравнения представляются как нечто само собой разумеющееся. Но при этом в коэффициентах зачастую возникают такие большие числа, что работать с ними большинство учеников… просто не готовы!

Попадётся вам, к примеру, такая задачка:

Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 82 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 25 минут позже автомобилиста. Ответ дайте в км/ч.

Это не моя разыгравшаяся фантазия, а вполне реальная задачка из ЕГЭ, между прочим.)

Кто в курсе, как решать текстовые задачи на движение, тот без труда составит вот такое уравнение:

Классическое дробно-рациональное уравнение. Здесь х — скорость велосипедиста. Немного повозившись с ним (избавившись от дробей и упростив всё до упора), получим вот такое квадратное уравнение:

Если начать решать это уравнение по-рабочекрестьянски, то получим, что дискриминант у него равен аж 13924! И… что? Как нам из такого здоровенного числа корень извлекать? Без калькулятора! Слабо? То-то…

Зато через теорему Виета это злое уравнение решается практически устно! Не верите? Что ж, смотрите сами…

Записываем сумму и произведение корней:

Осталось лишь догадаться, какие же числа дают в сумме минус 82, а в произведении минус 1800. Совсем чуточку подумав, довольно быстро получим, что:

Минус сто, ясное дело, нас не интересует (скорость не бывает отрицательной), а вот 18 км/ч — вполне себе правдоподобная велосипедная скорость.)

Вот и все дела.) И без долгих и утомительных вычислений, связанных с извлечением корня из пятизначного числа! Здорово, правда?

Посему, первые практические советы:

1. Если перед вами квадратное уравнение приведённого вида, то первым делом пробуем найти корни подбором. По теореме, ОБРАТНОЙ теореме Виета. В подавляющем большинстве заданий это срабатывает.

2. Не боимся уравнений с большими коэффициентами! Самое главное — не бросаемся считать дискриминант! Как правило, корни таких уравнений также довольно легко ищутся подбором.

Может, конечно, и не повезти, но зачем же такой шанс упускать, правда?)

Но есть у меня для вас хорошая новость.) Составители большинства заданий — люди гуманные.) И стараются составить уравнение так, чтобы корни являлись целыми числами и их легко можно было бы подобрать. Пробуем делать это!

Переходим к следующей полезной вещи.

Полезная вещь вторая — проверяем корни!

Теорему Виета можно применять не только для подбора корней, но и для проверки корней, найденных другим способом (через дискриминант, например). Решили уравнение — проверьте сумму и произведение корней! Всё срослось — значит, верно. Нет — значит, где-то накосячили. Ищите ошибку.)

Например, такое уравнение:

Дело нехитрое. Решаем себе через дискриминант, всё чин-чином, получаем корни:

x₁ = -7

x₂ = -3

Не бросаемся сразу же радостно писать ответ! Знаете поговорку доверяй, но проверяй?) Вот и не ленимся. Первым делом сложим наши корни:

Получили -10. Обратите внимание, не десять, а минус десять! Коэффициент b с противоположным знаком. Так уж теорема Виета устроена.)

Последняя (и окончательная) проверка — перемножим корни. Должен получиться свободный член:

Вот теперь всё хорошо.)

Более того, с этой благородной целью (проверка корней) теорему Виета можно применять и для неприведённых квадратных уравнений. Для любых. Да-да, я не шучу! Но эту фишку я оставлю на конец урока. На десерт.)

И что, думаете, только для подбора и проверки корней теорема Виета и нужна? Вовсе нет!

Полезная вещь третья — когда корни считать… не надо!

Вы спросите, а разве можно обойтись и вовсе без вычисления корней? Можно! Ещё как!)

Дискриминант — штука, безусловно, удобная, простая и понятная. С ним, как правило, всё легко и предсказуемо. Но… Может получиться какой-нибудь дурацкий дискриминант: 17 там, скажем, или 20. Что неизбежно приводит к появлению иррациональных корней, да…) А уж если в задании надо ещё что-то делать с корнями, то выражения с радикалами, даже для опытного ученика, могут перерасти в большую проблему. А для неопытного — вообще превратиться в полный ахтунг.

Но теорема Виета иногда способна на настоящие чудеса!

Например, такое задание:

Дано квадратное уравнение:

Найдите сумму квадратов корней, не находя самих корней.

Если сейчас начать решать это задание «в лоб» — считать дискриминант и искать корни уравнения по общей формуле, то получим вот таких двух красавцев:

Нам нужна сумма их квадратов. И что нам теперь с такими лохматыми числами делать?! Возводить в квадрат, складывать… Нет, возвести и сложить можно, конечно, но… не каждый ученик дорешает до конца это задание без ошибок!

Не отчаиваемся и читаем ещё раз условие. Обратите внимание, нам вообще НЕ сказано «решать уравнение», НЕ сказано «находить корни». Более того, нам прямым текстом говорится: «Найти сумму квадратов корней, не находя самих корней«.

Что делать? Как выкручиваться без поиска корней?

Посмотрим ещё раз на уравнение. Приведённое, между прочим.) Раз так, то, стало быть, для него справедлива теорема Виета!

Можно смело записать:

Вот так. Сумма корней — тройка, а произведение — единичка. Мы не знаем, чему равны сами эти корни, но у нас это и не спрашивают. Нас просят найти только сумму их квадратов.)

А вот теперь ключевой вопрос: А можно ли как-то расписать нужную нам сумму квадратов корней через сумму и произведение корней?

Да, можно! Кто на «ты» с формулами сокращённого умножения (а именно — с формулой квадрата суммы), тот, скорее всего, даже не заметит проблем.

Пишем:

Как я додумался до этого равенства? Очень просто. Вспомнил, что в формуле квадрата суммы сидят сумма квадратов и удвоенное произведение:

И выразил нужную величину (сумму квадратов) через остальные — сумму (т.е. квадрат суммы) и произведение (удвоенное).

Вот и всё, практически. Осталось лишь подставить тройку вместо суммы и единицу вместо произведения корней, да и посчитать, что получится:

Ответ: 7

И все дела.) И корни не понадобились! Вообще.) Мощная штука — теорема Виета! Ну и формулы сокращённого умножения, само собой.)

Этот приём — выражение какой-то сложной конструкции через сумму и произведение корней — очень популярен в заданиях на теорему Виета! Я уж молчу про более серьёзные задания. Например, задачи с параметрами, там этот финт ушами используется на полную катушку.)

Запоминаем:

В серьёзных заданиях на сумму и произведение корней пользуемся формулами сокращённого умножения и алгеброй 7-го класса! Здорово помогает.)

Как работать с неприведёнными уравнениями?

Как известно, самое сладкое — в конце трапезы. Обещанный десерт.)

Во всех примерах этого урока мы работали лишь с приведёнными квадратными уравнениями. Такими, у которых коэффициент при квадрате икса — единичка. А если уравнение не является приведённым? Т.е. а≠1? Что тогда? Про теорему Виета можно забыть?

Нет, забывать мы не будем. Мы поступим мудро и красиво. Раз уравнение не является приведённым, то мы его… сделаем! Как? Очень просто! Берём квадратное уравнение в общем виде:

и… делим обе части на «а»! Очищаем квадрат икса от коэффициента. Можно ли так делать? Конечно! Мы ведь с вами уже в курсе, что a никогда не бывает равно нулю (а≠0). Иначе уравнение будет не квадратным, а линейным. Вот и делим смело. Это совершенно безопасно. Естественно, все остальные слагаемые тоже придётся поделить на а, от этого никак не отвертишься.

Получим:

Вот и всё. Уравнение стало приведённым. Коэффициенты, правда, дробными стали, но тут уж ничего не поделать, да…) В этом новом уравнении в роли нового «b« выступает дробь b/a, а в роли нового свободного члена — дробь c/a. Можно записывать теорему Виета:

Вот так. Такая модифицированная запись теоремы Виета — более общая. Для любых квадратных уравнений годится — как приведённых (а=1), так и обычных (а≠1). С той лишь разницей, что при а=1 знаменатели исчезают — и теорема обретает свой привычный вид.

Имеет смысл запомнить эту общую форму записи: и для банальной проверки корней пригодится, и, опять же, для более солидных заданий на квадратные уравнения.

Например, надо решить уравнение:

Решаем, получаем корни:

Предположим, вам захотелось проверить, правильно ли вы нашли ваши иксы. Для этого, знамо дело, их надо подставить в исходное уравнение и посчитать результат. Но корни — дробные. Подставлять да считать долго и муторно…

Как проверить корни быстро и с минимумом вычислений? Не проблема! Записываем обобщённую теорему Виета для а=6:

И работаем. Складываем корни:

Так, по сумме всё проходит. Осталось перемножить:

И тут полный порядок! Значит, всё правильно.)

Очередной практический совет:

Найденные корни стараемся проверять! По сумме и произведению. Это здорово уменьшает количество ошибок при решении квадратных уравнений. Если уравнение не является приведённым, то для проверки пользуемся соответствующей модифицированной теоремой Виета.

Итак, мы с вами выяснили, что теорема Виета — штука простая. И очень полезная. И это не только трафаретное решение квадратных уравнений! В ВУЗе, при работе со всякими там пределами, интегралами, дифференциальными уравнениями и прочими прелестями высшей математики, вы ещё не раз вспомните добрым словом знаменитого французского математика с его теоремой.)

Ну что, порешаем?

1. Найдите подбором корни уравнений:

Ответы (в беспорядке):

2. Сумма катетов прямоугольного треугольника равна 23 см, а гипотенуза равна 17 см. Найдите больший катет треугольника.

3. Разность корней уравнения 2х² — 5х + с = 0 равна 1,5. Найдите с.

4. Дано уравнение: x² — 6x + 4 = 0. Не решая уравнения, найдите сумму кубов его корней.

5. Известно, что х₁ и х₂ — корни уравнения х²-18х+11 = 0.

Найдите значение выражения:

Ответы (в беспорядке):

144; 15; -1; 1

Всё сошлось? Рад за вас! Значит, отныне теорема Виета — не ваша очередная головная боль, а новый надёжный друг и помощник при решении уравнений (и не только квадратных, между прочим!).

Задания 4 и 5 не идут? Корни иррациональные получаются? Это специально.) Да и не нужны они вам… Да, есть там одна загвоздочка. Но алгебра седьмого класса и действия с дробями вам помогут! И этот урок, само собой. И всё получится.)

Источник

Что такое квадратные уравнения?

А теперь подробно с примерами обсудим квадратные уравнения.

Любые уравнения, сводящиеся к виду (ax^2+bx+c=0), называются квадратными. Где буквы ( b,; с) — любые числа, (aneq0). Почему (aneq0) мы обсудим ниже.

Обратите внимание на порядок слагаемых в квадратном уравнении:
(a) — всегда стоит первая и обязательно умножается на (x^2), она называется старшим коэффициентом (или первым);
(b) — принадлежит второму слагаемому и всегда умножается просто на переменную (x), это у нас второй коэффициент;
(c) — называют свободным членом, она не умножается ни на какую переменную.

В дальнейшем старайтесь приводить квадратное уравнение к виду (ax^2+bx+c=0), чтобы слагаемые стояли именно в таком порядке. Это очень важно при решении уравнений, и поможет избежать множества ошибок.

Потренируемся определять значения коэффициентов ( a, ; b,; с), чтобы запомнить порядок:

Пример 1
$$2x^2+3x+4=0;$$
$$a=2 quad b=3 quad c=4.$$

Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 quad b=-3 quad c=-0,7.$$

Пример 3
$$-x^2+2x+10=0;$$
Минус перед (x^2) можно представить в виде (-x^2=-1*x^2). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что (a=-1):
$$a=-1 quad b=2 quad c=10.$$

Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 quad b=-5 quad c=3.$$

Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена (c), поэтому он будет равен (0):
$$a=2 quad b=-3 quad c=0.$$

Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента (b):
$$a=-4 quad b=0 quad c=1.$$

Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты (b) или (c) равны нулю.

А вот если в уравнении коэффициенты ( a, ; b,; с) не равны 0, то такое уравнение называется полным.

От того, полное ли квадратное уравнение или неполное, зависит, как мы будем его решать. Начнем с неполных уравнений, они немного легче, но почему-то как раз в них все часто ошибаются.

Неполные квадратные уравнения

Неполное квадратное уравнение — это уравнение, в котором один из коэффициентов (b) или (c) равен нулю, (aneq0).

Как решать квадратное уравнение (ax^2+bx=0)?

Рассмотрим уравнение, в котором (c=0), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель (x) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: (x) и ((ax+b)). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=frac{-b}{a};$$

Получили, что уравнение имеет сразу два корня:(x=0) и (x=frac{-b}{a}).

Разберем на примере:

Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель (x):
$$x(2x+8)=0;$$
$$quad x_1=0 quad и quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: (x_1=0 quad и quad x_2=-4.)

Как решать квадратное уравнение (ax^2+с=0)?

Вот с такими уравнениями надо быть очень внимательными. Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным.

Общая схема решения уравнений вида (ax^2+с=0):

Выражаем (x^2) из уравнения:
$$ax^2+c=0;$$
$$ax^2=-c;$$
$$x^2=frac{-c}{a};$$
Если (-frac{c}{a} geq 0):
$$x_1=sqrt{-frac{c}{a}};$$
$$x_2=-sqrt{-frac{c}{a}};$$
Если (-frac{c}{a} lt 0):
РЕШЕНИЙ НЕТ.

Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=frac{8}{2};$$
$$x^2=4;$$
$$x=pmsqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: (x_1=2 quad и quad x_2=-2.)

Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=frac{-36}{2}=-18;$$
Так как (-18 < 0), а (x^2) не может быть отрицательным, то это уравнение не имеет корней.
Ответ: Нет корней.

Пример 10
$$frac{1}{2}x^2-frac{1}{18}=0;$$
$$frac{1}{2}x^2=frac{1}{18};$$
Чтобы избавиться от (frac{1}{2}), умножим уравнение слева и справа на (2):
$$x^2=frac{2}{18};$$
$$x^2=frac{1}{9};$$
$$x=pmsqrt{frac{1}{9}};$$
$$x_1=frac{1}{3};$$
$$x_2=-frac{1}{3};$$
Ответ: (x_1=frac{1}{3} quad и quad x_2=-frac{1}{3}.)

Решение квадратных уравнений через дискриминант

Квадратные уравнения (ax^2+bx+c=0), у которых все коэффициенты ( a, ; b,; с) не равны 0, называются полными квадратными уравнениями.

Чтобы их решать, нужно уметь находить дискриминант квадратного уравнения. Ничего страшного в этом нет, несмотря на странное называние. Дискриминантом уравнения (ax^2+bx+c=0) называют выражение:
$$D=b^2-4ac;$$

Если дискриминант получился больше нуля ((D ge 0)), то квадратное уравнение имеет два корня, которые можно найти по формулам:
$$x_1=frac{-b+sqrt{D}}{2a};$$
$$x_2=frac{-b-sqrt{D}}{2a};$$
Если дискриминант равен нулю ((D=0)), то квадратное уравнение имеет один корень:
$$x=frac{-b}{2a};$$
Если дискриминант меньше нуля ((D<0)), то квадратное уравнение не имеет корней.

Примеры квадратных уравнений

Пример 11
$$2x^2-9x+4=0;$$
Прежде чем решать уравнение, я рекомендую выписать все коэффициенты:
$$a=2 quad b=-9 quad c=4.$$
Используя значения коэффициентов, можем посчитать дискриминант:
$$D=b^2-4ac=(-9)^2-4*2*4=81-32=49;$$
Ура, дискриминант посчитан и он больше нуля! Значит корней будет два, найдем их по формулам:
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-9)+sqrt{49}}{2*2}=frac{9+7}{4}=frac{16}{4}=4;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-9)—sqrt{49}}{2*2}=frac{9-7}{4}=frac{2}{4}=frac{1}{2};$$
Ответ: (x_1=4 quad и quad x_2=frac{1}{2}.)

Пример 12
$$10x^2+x-21=0;$$
$$a=10 quad b=1 quad c=-21.$$
$$D=b^2-4ac=1^2-4*10*(-21)=1+840=841;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-1+sqrt{841}}{2*10}=frac{-1+29}{20}=frac{28}{20}=frac{7}{5};$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-1-sqrt{841}}{2*10}=frac{-1-29}{20}=frac{-30}{20}=frac{-3}{2};$$
Ответ: (x_1=frac{7}{5} quad и quad x_2=-frac{3}{2}.)

Пример 13
$$(x-7)^2=2x^2+11x+23;$$
Это уравнение еще нужно привести к стандартному виду, для этого раскроем скобки по формуле «квадрат разности» ((a-b)^2=a^2-2ab+b^2):
$$x^2-14x+49=2x^2+11x+23;$$
Перекинем все слагаемые в левую часть, не забывая при этом менять знак на противоположный:
$$x^2-14x+49-2x^2-11x-23=0;$$
Приводим подобные слагаемые:
$$-x^2-25x+26=0;$$
$$a=-1 quad b=-25 quad c=26.$$
$$D=b^2-4ac=(-25)^2-4*(-1)*26=625+104=729;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-25)+sqrt{729}}{2*(-1)}=frac{25+27}{-2}=frac{52}{-2}=-26;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-25)-sqrt{729}}{2*(-1)}=frac{25-27}{-2}=frac{-2}{-2}=1;$$
Ответ: (x_1=-26 quad и quad x_2=1.)

Пример 14
$$3x^2+7x+6=0;$$
$$a=3 quad b=7 quad c=6.$$
$$D=b^2-4ac=7^2-4*3*6=49-72=-23;$$
Стоп! Дискриминант получился отрицательный, это означает, что у этого квадратного уравнения не будет корней.
Ответ: Нет корней.

Пример 15
$$4x^2-4x+1=0;$$
$$a=4 quad b=-4 quad c=1.$$
$$D=b^2-4ac=(-4)^2-4*4*1=16-16=0;$$
Дискриминат получился равен нулю. В этом случае у квадратного уравнения будет всего один корень, который можно найти по формуле:
$$x=frac{-b}{2a}=frac{-(-4)}{2*4}=frac{4}{8}=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)

Полезно знать! Если дискриминант получился равен нулю, то перед вами формула полного квадрата. Это значит, что квадратный многочлен можно разложить по формуле ((apm b)^2=a^2pm 2ab+b^2).
И пример №15 можно решить, используя эту формулу:
$$4x^2-4x+1=0;$$
$$(2x-1)^2=0;$$
Квадрат равен нулю только в том случае, если выражение под квадратом равно нулю:
$$2x-1=0;$$
$$2x=1;$$
$$x=frac{1}{2};$$
Ответ получили точно такой же, как и при решении через дискриминант.

Дискриминант деленный на 4

Квадратные уравнения иногда удобно решать по упрощенной формуле дискриминанта. Но применять ее можно не во всех случаях, а только, если коэффициент (b) в уравнении (ax^2+bx+c=0) четный (делится на 2).

Итак, представим, что коэффициент (b) четный, тогда дискриминант можно посчитать по формуле:
$$D_4=left(frac{b}{2}right)^2-ac;$$
А корни уравнения находятся по формулам:
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a};$$
Кстати, обычный дискриминант (D) отличается от (D_4) в 4 раза:
$$D_4=frac{D}{4}=frac{b^2-4ac}{4}=frac{b^2}{4}-frac{4ac}{4}=left(frac{b}{2}right)^2-ac;$$
Поэтому (D_4) называют «дискриминантом деленным на 4».

Эти формулы нужны, чтобы, когда это возможно, сократить вычисления. Разберем на примере:

Пример 16
$$7x^2-20x-1067=0;$$
$$a=7 quad b=-20 quad c=-1067.$$
(b=-20) — четный, поэтому воспользуемся дискриминантом деленным на 4:
$$D_4=left(frac{b}{2}right)^2-ac=left(frac{-20}{2}right)^2-7*(-1067)=(-10)^2+7469=100+7469=7569;$$
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a}=frac{-frac{-20}{2}+sqrt{7569}}{7}=frac{10+87}{7}=frac{97}{7};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a}=frac{-frac{-20}{2}-sqrt{7569}}{7}=frac{10-87}{7}=frac{-77}{7}=-11;$$
Ответ: (x_1=frac{97}{7} quad и quad x_2=-11.)

Возникает вопрос, зачем вообще нужен этот (D_4), если все можно считать через обычный дискриминант? Если бы мы считали пример №16 как обычно, то наш дискриминант, который и так получился не маленьким — ((D_4=7659)), был бы в четыре раза больше. А чем больше числа, тем сложнее расчеты.

Теорема Виета для решения квадратных уравнений

Теорема Виета — это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.

Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.

Приведенное квадратное уравнение

Квадратные уравнения (ax^2+bx+c=0), у которых коэффициент (a) при (x^2) равен (1), называют приведенными.

Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент (a):

Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на (a=3). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$frac{3x^2-15x+9}{3}=frac{0}{3};$$
В результате каждое слагаемое поделится на (3):
$$frac{3x^2}{3}-frac{15x}{3}+frac{9}{3}=0;$$
$$x^2-5x+3=0;$$

Формулы Виета

Сумма корней приведенного квадратного уравнения (x^2+bx+c=0) равна второму коэффициенту (b) со знаком минус, а произведение корней равно свободному члену (c).

Пусть (x_1), и (x_2) — корни квадратного уравнения (x^2+bx+c=0), тогда справедливы формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:

Пример 18
$$x^2+4x+3=0;$$
$$a=1 quad b=4 quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
Подставим коэффициенты:
$$ begin{cases}
x_1+x_2=-4; \
x_1*x_2=3. \
end{cases}$$

Нужно найти такие (x_1) и (x_2), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении (3ку)?

Либо: (3=1*3);
Либо: (3=(-1)*(-3)).

Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: (x_1=-1) и (x_2=-3). А самое главное, мы нашли корни исходного квадратного уравнения.
Ответ: (x_1=-1 quad и quad x_2=-3.)

Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену (c), а сумма корней равна ((-b)).

Теорема Виета, если (aneq1)

По теореме Виета можно решать не только приведенные квадратные уравнения (у которых (a=1)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент (a):
$$ax^2+bx+c=0; quad mid :a$$
$$frac{ax^2}{a}+frac{bx}{a}+frac{c}{a};$$
$$x^2+frac{b}{a}*x+frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет (frac{b}{a}), а свободным членом (frac{c}{a}):
$$ begin{cases}
x_1+x_2=-frac{b}{a}; \
x_1*x_2=frac{c}{a}. \
end{cases}$$

Пример 19
$$12x^2+x-1=0;$$
$$a=12 quad b=1 quad c=-1.$$
Коэффициент (a=12 neq 1), поэтому разделим все уравнение на (a=12):
$$12x^2+x-1=0; quad mid :12$$
$$x^2+frac{1}{12}x-frac{1}{12}=0;$$
$$a=1 quad b=frac{1}{12} quad c=-frac{1}{12}.$$

Теорема Виета:
$$ begin{cases}
x_1+x_2=-frac{1}{12}; \
x_1*x_2=-frac{1}{12}. \
end{cases}$$

Подбираем корни:
$$x_1=-frac{1}{3};$$
$$x_2=frac{1}{4};$$

Ответ: (x_1=-frac{1}{3} quad и quad x_2=frac{1}{4}.)

Теорема Виета удобна, когда у квадратного уравнения небольшие коэффициенты и можно легко подобрать корни. В остальных случаях лучше пользоваться дискриминантом.

Источник

Определение

Уравнение вида ax²+bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b²–4ac

Если D>0, то уравнение имеет два различных корня. Их находят по формуле:

Если D<0, то уравнение не имеет корней.
Если D=0, то уравнение имеет два равных корня, их записывают и находят как один:

Рассмотрим решение квадратных уравнений на примерах.

Пример №1. Решить уравнение х²–2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b²–4ac=(–2)²–41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х²+2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b²–4ac=2²–4=4–20=–16, D<0, уравнение не имеет корней.

Пример №3. Решить уравнение х²–6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b²–4ac=(–6)²–4=36–36=0, D=0, 1 корень

Теорема Виета

Приведенные квадратные уравнения

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

х₁+х₂= –b

х₁•х₂= с

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х²–10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

х₁+х₂=–(–10)=10

х₁х₂=21

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х²+5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

х₁+х₂=–5

х₁х₂=4

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

–1+(–4)=–5

(–1)(–4)=4

Ответ: –1 и –4

Задание OM2002

Решить уравнение: х2−2х+√5−х=√5−х+24

Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5−х≥0

Решаем полученное неравенство: −х≥−5, отсюда х≤5. Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х2−2х+√5−х − √5−х− 24=0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х2−2х− 24=0

Итак, корнями уравнения х2−2х− 24=0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 не≤5, а число минус 4 записываем в ответ нашего уравнения, так как −4≤5 .

Ответ: -4

pазбирался: Даниил Романович | обсудить разбор

Алла Василевская | Просмотров: 13k

Источник

Решение неполных квадратных уравнений

Как решить уравнение ax 2 = 0

Как решить уравнение ax 2 + с = 0

Как решить уравнение ax 2 + bx = 0

Как разложить квадратное уравнение

Дискриминант: формула корней квадратного уравнения

Алгоритм решения квадратных уравнений по формулам корней

Примеры решения квадратных уравнений

Формула корней для четных вторых коэффициентов

Формула Виета

Упрощаем вид квадратных уравнений

Связь между корнями и коэффициентами

Решение квадратных уравнений: формула корней, примеры

Квадратное уравнение, его виды

Приведенные и неприведенные квадратные уравнения

Полные и неполные квадратные уравнения

Решение неполных квадратных уравнений

Решение уравнения a·x 2 =0

Решение уравнения a · x 2 + c = 0

Решение уравнения a·x 2 +b·x=0

Дискриминант, формула корней квадратного уравнения

Вывод формулы корней квадратного уравнения

Алгоритм решения квадратных уравнений по формулам корней

Примеры решения квадратных уравнений

Формула корней для четных вторых коэффициентов

Упрощение вида квадратных уравнений

Связь между корнями и коэффициентами

Решение неполных квадратных уравнений

Как решить уравнение ax 2 = 0

Как решить уравнение ax 2 + с = 0

Как решить уравнение ax 2 + bx = 0

Как разложить квадратное уравнение

Дискриминант: формула корней квадратного уравнения

Алгоритм решения квадратных уравнений по формулам корней

Примеры решения квадратных уравнений

Формула корней для четных вторых коэффициентов

Формула Виета

Упрощаем вид квадратных уравнений

Связь между корнями и коэффициентами

«Решение квадратных уравнений с помощью свойств коэффициентов» план-конспект занятия по алгебре (8 класс) на тему

Скачать:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

№70-71 обобщающий урок по теме «Решение квадратных уравнений при помощи формул» 8 класс

Комплексные числа. Лекция 2. Решение квадратных уравнений с действительными и комплексными коэффициентами.

конспект урока по алгебре 8 класс «Решение квадратных уравнений с четным вторым коэффициентом»

Урок алгебры в 8 классе по теме «Решение квадратных уравнений с помощью формул»

Методическая разработка урока алгебры в 8 классе по теме «Решение квадратных уравнений при помощи формул»

Презентация по теме «Решение квадратных уравнений с помощью переноса старшего коэффициента»

Что такое квадратные уравнения?

Неполные квадратные уравнения

Как решать квадратное уравнение (ax^2+bx=0)?

Как решать квадратное уравнение (ax^2+с=0)?

Решение квадратных уравнений через дискриминант

Примеры квадратных уравнений

Дискриминант деленный на 4

Теорема Виета для решения квадратных уравнений

Приведенное квадратное уравнение

Формулы Виета

Теорема Виета, если (aneq1)

Дискриминант

Теорема Виета

Не пропустите также:

«Решение квадратных уравнений с помощью свойств коэффициентов»
план-конспект занятия по алгебре (8 класс) на тему