Факториал натурального числа n (обозначение – “n!“) равен произведению всех натуральных чисел от 1 до n включительно.
n! = 1 * 2 * 3 * 4 … * n
Ниже представлены таблицы с факториалами чисел от 1 до 20 (точные значения) и от 21 до 100 (приближенные значения).
- 1. Факториалы чисел от 1 до 20
- 2. Факториалы чисел от 21 до 100
1. Факториалы чисел от 1 до 20
| Факториал числа n (n!) |
Значение |
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40320 |
| 9! | 362880 |
| 10! | 3628800 |
| 11! | 39916800 |
| 12! | 479001600 |
| 13! | 6227020800 |
| 14! | 87178291200 |
| 15! | 1307674368000 |
| 16! | 20922789888000 |
| 17! | 355687428096000 |
| 18! | 6402373705728000 |
| 19! | 121645100408832000 |
| 20! | 2432902008176640000 |
microexcel.ru
2. Факториалы чисел от 21 до 100
Факториал – это быстрорастущая функция, и начиная с определенного n значения достаточно велики. Поэтому в математических вычислениях удобнее пользоваться приближенными значениями для больших чисел.
| Факториал числа n (n!) |
Приближенное значение |
| 21! | 5,10909 ⋅ 1019 |
| 22! | 1,124 ⋅ 1021 |
| 23! | 2,5852 ⋅ 1022 |
| 24! | 6,20448 ⋅ 1023 |
| 25! | 1,55112 ⋅ 1025 |
| 26! | 4,03291 ⋅ 1026 |
| 27! | 1,08889 ⋅ 1028 |
| 28! | 3,04888 ⋅ 1029 |
| 29! | 8,84176 ⋅ 1030 |
| 30! | 2,65253 ⋅ 1032 |
| 31! | 8,22284 ⋅ 1033 |
| 32! | 2,63131 ⋅ 1035 |
| 33! | 8,68332 ⋅ 1036 |
| 34! | 2,95233 ⋅ 1038 |
| 35! | 1,03331 ⋅ 1040 |
| 36! | 3,71993 ⋅ 1041 |
| 37! | 1,37638 ⋅ 1043 |
| 38! | 5,23023 ⋅ 1044 |
| 39! | 2,03979 ⋅ 1046 |
| 40! | 8,15915 ⋅ 1047 |
| 41! | 3,34525 ⋅ 1049 |
| 42! | 1,40501 ⋅ 1051 |
| 43! | 6,04153 ⋅ 1052 |
| 44! | 2,65827 ⋅ 1054 |
| 45! | 1,19622 ⋅ 1056 |
| 46! | 5,50262 ⋅ 1057 |
| 47! | 2,58623 ⋅ 1059 |
| 48! | 1,24139 ⋅ 1061 |
| 49! | 6,08282 ⋅ 1062 |
| 50! | 3,04141 ⋅ 1064 |
| 51! | 1,55112 ⋅ 1066 |
| 52! | 8,06582 ⋅ 1067 |
| 53! | 4,27488 ⋅ 1069 |
| 54! | 2,30844 ⋅ 1071 |
| 55! | 1,26964 ⋅ 1073 |
| 56! | 7,10999 ⋅ 1074 |
| 57! | 4,05269 ⋅ 1076 |
| 58! | 2,35056 ⋅ 1078 |
| 59! | 1,38683 ⋅ 1080 |
| 60! | 8,32099 ⋅ 1081 |
| 61! | 5,0758 ⋅ 1083 |
| 62! | 3,147 ⋅ 1085 |
| 63! | 1,98261 ⋅ 1087 |
| 64! | 1,26887 ⋅ 1089 |
| 65! | 8,24765 ⋅ 1090 |
| 66! | 5,44345 ⋅ 1092 |
| 67! | 3,64711 ⋅ 1094 |
| 68! | 2,48004 ⋅ 1096 |
| 69! | 1,71122 ⋅ 1098 |
| 70! | 1,1979 ⋅ 10100 |
| 71! | 8,5048 ⋅ 10101 |
| 72! | 6,1234 ⋅ 10103 |
| 73! | 4,4701 ⋅ 10105 |
| 74! | 3,3079 ⋅ 10107 |
| 75! | 2,4809 ⋅ 10109 |
| 76! | 1,8855 ⋅ 10111 |
| 77! | 1,4518 ⋅ 10113 |
| 78! | 1,1324 ⋅ 10115 |
| 79! | 8,9462 ⋅ 10116 |
| 80! | 7,1569 ⋅ 10118 |
| 81! | 5,7971 ⋅ 10120 |
| 82! | 4,7536 ⋅ 10122 |
| 83! | 3,9455 ⋅ 10124 |
| 84! | 3,3142 ⋅ 10126 |
| 85! | 2,8171 ⋅ 10128 |
| 86! | 2,4227 ⋅ 10130 |
| 87! | 2,1078 ⋅ 10132 |
| 88! | 1,8548 ⋅ 10134 |
| 89! | 1,6508 ⋅ 10136 |
| 90! | 1,4857 ⋅ 10138 |
| 91! | 1,352 ⋅ 10140 |
| 92! | 1,2438 ⋅ 10142 |
| 93! | 1,1568 ⋅ 10144 |
| 94! | 1,0874 ⋅ 10146 |
| 95! | 1,033 ⋅ 10148 |
| 96! | 9,9168 ⋅ 10149 |
| 97! | 9,6193 ⋅ 10151 |
| 98! | 9,4269 ⋅ 10153 |
| 99! | 9,3326 ⋅ 10155 |
| 100! | 9,3326 ⋅ 10157 |
microexcel.ru

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Таблица факториалов
Понятие факториала определено только для целых неотрицательных чисел.
Принято считать, что .
Таблица факториалов натуральных чисел от 1 до 50
Приведем точные значения факториалов натуральных чисел от 1 до 50
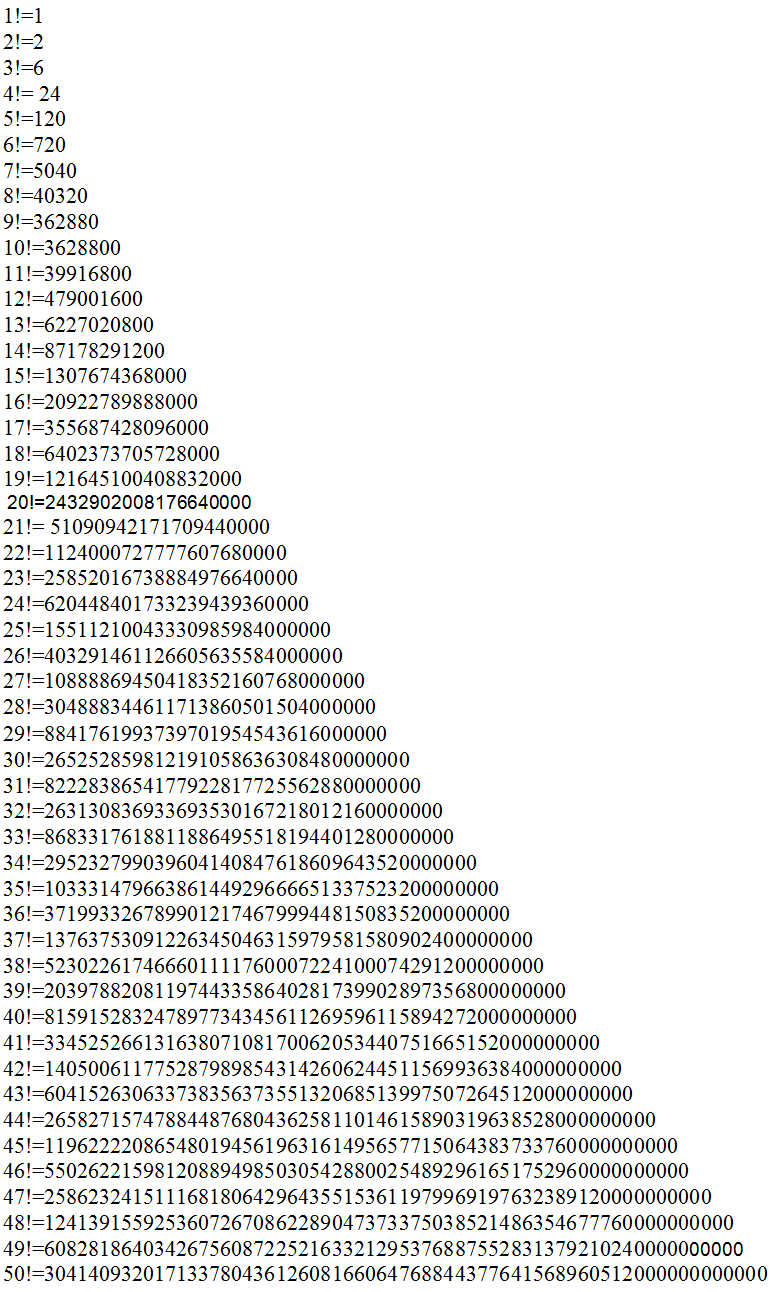
Так как факториал является быстро растущей функцией, т.е его значения начиная с некоторого очень велики, то в математических расчетах удобно пользоваться следующими значениями факториала, которые собраны в следующей таблице для чисел от 1 до 100:
| Понравился сайт? Расскажи друзьям! | |
Таблица значений факториала от 0 до 100
| n | n! |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
| 21 | 51090942171709400000 |
| 22 | 1124000727777610000000 |
| 23 | 25852016738885000000000 |
| 24 | 620448401733239000000000 |
| 25 | 15511210043331000000000000 |
| 26 | 403291461126606000000000000 |
| 27 | 10888869450418400000000000000 |
| 28 | 304888344611714000000000000000 |
| 29 | 8841761993739700000000000000000 |
| 30 | 265252859812191000000000000000000 |
| 31 | 8222838654177920000000000000000000 |
| 32 | 263130836933694000000000000000000000 |
| 33 | 8683317618811890000000000000000000000 |
| 34 | 295232799039604000000000000000000000000 |
| 35 | 10333147966386100000000000000000000000000 |
| 36 | 371993326789901000000000000000000000000000 |
| 37 | 13763753091226300000000000000000000000000000 |
| 38 | 523022617466601000000000000000000000000000000 |
| 39 | 20397882081197400000000000000000000000000000000 |
| 40 | 815915283247898000000000000000000000000000000000 |
| 41 | 33452526613163800000000000000000000000000000000000 |
| 42 | 1405006117752880000000000000000000000000000000000000 |
| 43 | 60415263063373800000000000000000000000000000000000000 |
| 44 | 2658271574788450000000000000000000000000000000000000000 |
| 45 | 119622220865480000000000000000000000000000000000000000000 |
| 46 | 5502622159812090000000000000000000000000000000000000000000 |
| 47 | 258623241511168000000000000000000000000000000000000000000000 |
| 48 | 12413915592536100000000000000000000000000000000000000000000000 |
| 49 | 608281864034268000000000000000000000000000000000000000000000000 |
| 50 | 30414093201713400000000000000000000000000000000000000000000000000 |
| 51 | 1551118753287380000000000000000000000000000000000000000000000000000 |
| 52 | 80658175170943900000000000000000000000000000000000000000000000000000 |
| 53 | 4274883284060020000000000000000000000000000000000000000000000000000000 |
| 54 | 230843697339241000000000000000000000000000000000000000000000000000000000 |
| 55 | 12696403353658300000000000000000000000000000000000000000000000000000000000 |
| 56 | 710998587804863000000000000000000000000000000000000000000000000000000000000 |
| 57 | 40526919504877200000000000000000000000000000000000000000000000000000000000000 |
| 58 | 2350561331282880000000000000000000000000000000000000000000000000000000000000000 |
| 59 | 138683118545690000000000000000000000000000000000000000000000000000000000000000000 |
| 60 | 8320987112741390000000000000000000000000000000000000000000000000000000000000000000 |
| 61 | 507580213877225000000000000000000000000000000000000000000000000000000000000000000000 |
| 62 | 31469973260387900000000000000000000000000000000000000000000000000000000000000000000000 |
| 63 | 1982608315404440000000000000000000000000000000000000000000000000000000000000000000000000 |
| 64 | 126886932185884000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 65 | 8247650592082470000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 66 | 544344939077443000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 67 | 36471110918188700000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 68 | 2480035542436830000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 69 | 171122452428141000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 70 | 11978571669969900000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 71 | 850478588567862000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 72 | 61234458376886100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 73 | 4470115461512690000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 74 | 330788544151939000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 75 | 24809140811395400000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 76 | 1885494701666050000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 77 | 145183092028286000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 78 | 11324281178206300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 79 | 894618213078298000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 80 | 71569457046263800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 81 | 5797126020747370000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 82 | 475364333701284000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 83 | 39455239697206600000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 84 | 3314240134565350000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 85 | 281710411438055000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 86 | 24227095383672700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 87 | 2107757298379530000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 88 | 185482642257398000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 89 | 16507955160908500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 90 | 1485715964481760000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 91 | 135200152767840000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 92 | 12438414054641300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 93 | 1156772507081640000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 94 | 108736615665674000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 95 | 10329978488239100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 96 | 991677934870949000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 97 | 96192759682482200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 98 | 9426890448883250000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 99 | 933262154439442000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
| 100 | 93326215443944200000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 |
Хорошая задача. Сразу вспоминается, как учительница в 3 классе (!) задала задачу: «сколько цифр у числа, образованного произведением всех натуральных чисел от 1 до 100. Я решила эту задачу за одну минуту. » Я эту задачу решил только спустя 5 лет, когда открыл для себя логарифмы и таблицу Брадиса =) (тогда еще не было у простых смертных персональных компьютеров) . Но не суть.
Начну со второго вопроса, т. к. он попроще.
20 чисел из первых 100 чисел делятся на 5, но из них четыре числа, а именно 25, 50, 75 и 100 содержат по два множителя 5. Итак, 100! будет оканчиваться на 24 нуля. Тут все понятно.
Теперь как найти Факториал 100!
Задача решения факториала оказалась настолько сложной, что точной формулы его нахождения нет до сих пор, но можно привести формулу Стирлинга для приблизительного вычисления факториала:
Она дает результат: 100! ≈ 9,33×10157
Факториал
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
- Чтобы вычислить 6!, нужно 5!=120 умножить на 6, получается 720
- Чтобы вычислить 8!, нужно 7!=5040 умножить на 8, получается 40.320
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
Которое означает:
«факториал любого числа — это число, умноженное на факториал предыдущего целого числа»
Итак, 12! = 12 × 11!, . и 100! = 100 × 99!, и т. д.
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Сколько существует разных способов, с помощью которых 7 человек могут прийти первым, вторым и третьим ?
Список довольно длинный, если 7 человек обозначим как a, b, c, d, e, f и g, то список включает:
abc, abd, abe, abf, abg, acb, acd, ace, acf, . и т. д.
Формула для расчета: 7!/(7−3)! = 7!/4!
Выпишем умножение полностью:
(7 × 6 × 5 × 4 × 3 × 2 × 1)/(4 × 3 × 2 × 1) = 7 × 6 × 5
Пояснение: 4 × 3 × 2 × 1 сокращено, т.к. они встречаются в числителе и знаменателе, и осталось только 7 × 6 × 5 . получаем:
7 × 6 × 5 = 210
Итак, есть 210 различных способов, которыми 7 человек могут прийти первым, вторым и третьим.
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
70! приблизительно 1,197857 . x 10 100 , что чуть больше, чем в Googol (цифра 1, за которой следует сотня нулей).
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10 157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10 374
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Наивный алгоритм
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
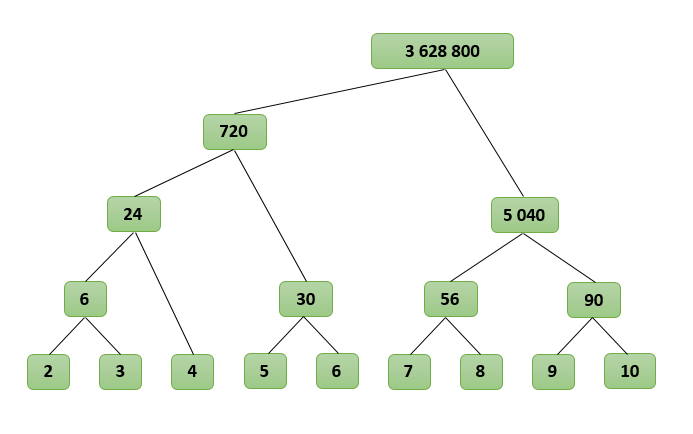
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Библиотека GMP
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
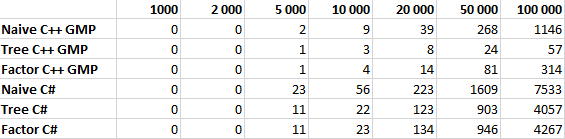
Сравнение производительности
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
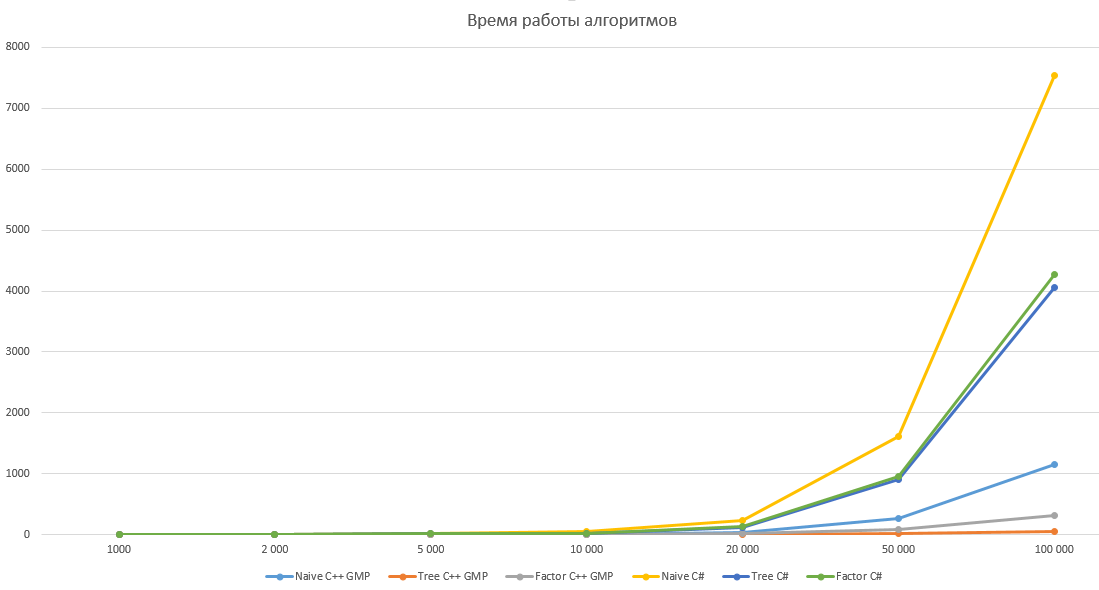
График с линейной шкалой
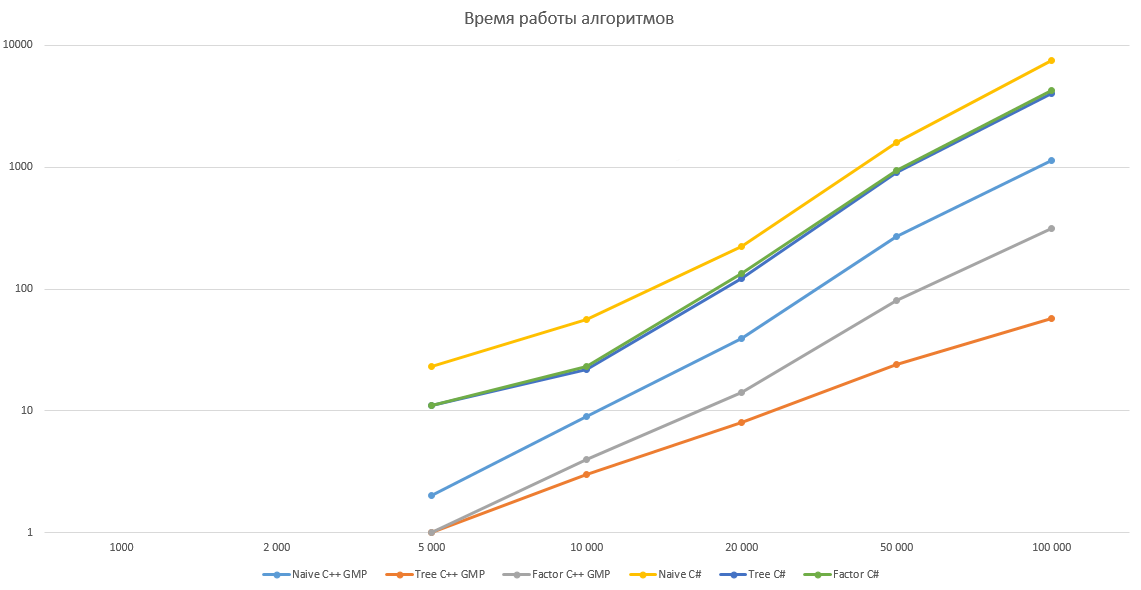
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
884 976 640 000
239 439 360 000
330 985 984 000 000
605 635 584 000 000
352 160 768 000 000
860 501 504 000 000
954 543 616 000 000
636 308 480 000 000
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021