Сумма натуральных делителей (С) — величина, которая для каждого натурального числа показывает, чему равна сумма всех его натуральных делителей.
С точки зрения математики С является мультипликативной арифметической функцией: для любых натуральных и взаимно простых a и b справедливо свойство мультипликативности С(a • b) = С(a) • С(b).
Другая, похожая величина — это сумма S(n) собственных делителей числа, меньших чем исходное число n (число 1, являющееся делителем любого числа, входит в эту сумму). Она отличается от С(n) на величину самого числа n: S(n) = С(n) — n. Вычисление S позволяет разбить множество натуральных чисел на 3 группы: совершенные числа — натуральные числа, равные сумме своих меньших делителей; избыточные числа — для которых сумма S(n) больше числа; недостаточные числа — для которых сумма S(n) меньше числа.
Количество делителей для первых натуральных чисел:
| n | С(n) | S(n) |
|---|---|---|
| 1 | 1 | 0 (1 — недостаточное число) |
| 2 | 1 + 2 = 3 | 1 (2 — недостаточное число) |
| 3 | 1 + 3 = 4 | 1 (3 — недостаточное число) |
| 4 | 1 + 2 + 4 = 7 | 3 (4 — недостаточное число) |
| 5 | 1 + 5 = 6 | 1 (5 — недостаточное число) |
| 6 | 1 + 2 + 3 + 6 = 12 | 6 (6 — совершенное число) |
| 7 | 1 + 7 = 8 | 1 (7 — недостаточное число) |
| 8 | 1 + 2 + 4 + 8 = 15 | 7 (8 — недостаточное число) |
| 9 | 1 + 3 + 9 = 13 | 4 (9 — недостаточное число) |
| 10 | 1 + 2 + 5 + 10 = 18 | 8 (10 — недостаточное число) |
| 11 | 1 + 11 = 12 | 1 (11 — недостаточное число) |
| 12 | 1 + 2 + 3 + 4 + 6 + 12 = 28 | 16 (12 — избыточное число) |
| 13 | 1 + 13 = 14 | 16 (13 — недостаточное число) |
| 14 | 1 + 2 + 7 + 14 = 24 | 10 (14 — недостаточное число) |
| 15 | 1 + 3 + 5 + 15 = 24 | 9 (15 — недостаточное число) |
Свойства[]
- Если n ― простое число, то C(n) = n + 1
- Все простые и полупростые числа являются недостаточными
См. также[]
- Количество натуральных делителей
- Функция Мёбиуса
- Функция Эйлера
Содержание материала
- Как определить количество делителей конкретного числа
- Видео
- Признаки делимости чисел
- Определение [ править
- Как найти число простых делителей числа
- Простые и составные числа
- Чем отличаются друг от друга, как найти
- Тест Миллера Рабина
Как определить количество делителей конкретного числа
Чтобы узнать, сколько положительных делителей у конкретного числа a, каноническое разложение которого выглядит как a = p 1 s 1 · p 2 s 2 · … · p n s n , нужно найти значение выражения ( s 1 + 1 ) · ( s 2 + 1 ) · … · ( s n + 1 ) . О количестве наборов переменных t 1 , t 2 , … , t n мы можем судить по величине записанного выражения.
Покажем на примере, как это вычисляется. Определим, сколько будет натуральных делителей у числа 3 900 , которое мы использовали в предыдущей задаче. Каноническое разложение мы уже записывали: 3 900 = 2 2 · 3 · 5 2 · 13 . Значит, s 1 = 2 , s 2 = 1 , s 3 = 2 , s 4 = 1 . Теперь подставим значения s 1 , s 2 , s 3 и s 4 в выражение ( s 1 + 1 ) · ( s 2 + 1 ) · ( s 3 + 1 ) · ( s 4 + 1 ) и вычислим его значение. Имеем ( 2 + 1 ) · ( 1 + 1 ) · ( 2 + 1 ) · ( 1 + 1 ) = 3 · 2 · 3 · 2 = 36 . Значит, это число имеет всего 36 делителей, являющихся натуральными числами. Пересчитаем то количество, что у нас получилось в предыдущей задаче, и убедимся в правильности решения. Если учесть и отрицательные делители, которых столько же, сколько и положительных, то получится, что у данного числа всего будет 72 делителя.
Условие: определите, сколько делителей имеет 84 .
Решение
Раскладываем число на множители.
84 42 21 7 1 2 2 3 7
Записываем каноническое разложение: 84 = 2 2 · 3 · 7 . Определяем, сколько у нас получится положительных делителей: ( 2 + 1 ) · ( 1 + 1 ) · ( 1 + 1 ) = 12 . Для учета отрицательных нужно умножить это число на 2 : 2 · 12 = 24 .
Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.
Видео
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Определение [ править
Функция «сумма положительных делителей »σx(n) для вещественного или комплексного числа x определяется как сумма x-х степеней положительных делителей числа n. Функцию можно выразить формулой
σ x ( n ) = ∑ d | n d x , <displaystyle sigma _(n)=sum _d^,!,>
где d | n <displaystyle > 
Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть делители, за исключением самого n [5] , и равна σ1(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.
Как найти число простых делителей числа
Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.
Для этого:
- 54 делим на «два» и получаем 27;
- 27 нечетное, поэтому разделим его уже не на «два», а на следующее простое число, т. е. «три»;
- заметим, что 27=33;
- таким образом, разложение 54 имеет вид 54 = 21 * 33, т.е. простые делители числа 54 — это «два» и «три».
Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p1*d1 p2d2*⋅ …⋅*pmdm, увеличенных на 1. Иными словами, в общем случае K = (d1+1)*…* (dm+1).
Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.
Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
- делитель — это число, НА которое делится заданное число;
- кратное — это число, которое само ДЕЛИТСЯ НА заданное число.
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Тест Миллера Рабина
В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.
Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.
Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2st.
Затем выбирается случайное число a, такое что 1<a<m. Если a не свидетельствует о простоте числа m, то программа должна выдать ответ «m составное» и завершить свою работу. В противном случае выбирается другое случайное число a и проверка повторяется снова. После того как будут установлены r свидетелей простоты, должен быть выдан ответ «m, вероятно, простое», и алгоритм завершит свою работу.
Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4-r).
Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.
Теги
Given a natural number n, the task is to find sum of divisors of all the divisors of n.
Examples:
Input : n = 54 Output : 232 Divisors of 54 = 1, 2, 3, 6, 9, 18, 27, 54. Sum of divisors of 1, 2, 3, 6, 9, 18, 27, 54 are 1, 3, 4, 12, 13, 39, 40, 120 respectively. Sum of divisors of all the divisors of 54 = 1 + 3 + 4 + 12 + 13 + 39 + 40 + 120 = 232. Input : n = 10 Output : 28 Divisors of 10 are 1, 2, 5, 10 Sums of divisors of divisors are 1, 3, 6, 18. Overall sum = 1 + 3 + 6 + 18 = 28
Using the fact that any number n can be expressed as product of prime factors, n = p1k1 x p2k2 x … where p1, p2, … are prime numbers.
All the divisors of n can be expressed as p1a x p2b x …, where 0 <= a <= k1 and 0 <= b <= k2.
Now sum of divisors will be sum of all power of p1 – p10, p11,…., p1k1 multiplied by all power of p2 – p20, p21,…., p2k1
Sum of Divisor of n
= (p10 x p20) + (p11 x p20) +…..+ (p1k1 x p20) +….+ (p10 x p21) + (p11 x p21) +…..+ (p1k1 x p21) +……..+
(p10 x p2k2) + (p11 x p2k2) +……+ (p1k1 x p2k2).
= (p10 + p11 +…+ p1k1) x p20 + (p10 + p11 +…+ p1k1) x p21 +…….+ (p10 + p11 +…+ p1k1) x p2k2.
= (p10 + p11 +…+ p1k1) x (p20 + p21 +…+ p2k2).
Now, the divisors of any pa, for p as prime, are p0, p1,……, pa. And sum of divisors will be (p(a+1) – 1)/(p -1), let it define by f(p).
So, sum of divisors of all divisor will be,
= (f(p10) + f(p11) +…+ f(p1k1)) x (f(p20) + f(p21) +…+ f(p2k2)).
So, given a number n, by prime factorization we can find the sum of divisors of all the divisors. But in this problem we are given that n is product of element of array. So, find prime factorization of each element and by using the fact ab x ac = ab+c.
Below is the implementation of this approach:
C++
#include<bits/stdc++.h>
using namespace std;
int sumDivisorsOfDivisors(int n)
{
map<int, int> mp;
for (int j=2; j<=sqrt(n); j++)
{
int count = 0;
while (n%j == 0)
{
n /= j;
count++;
}
if (count)
mp[j] = count;
}
if (n != 1)
mp[n] = 1;
int ans = 1;
for (auto it : mp)
{
int pw = 1;
int sum = 0;
for (int i=it.second+1; i>=1; i--)
{
sum += (i*pw);
pw *= it.first;
}
ans *= sum;
}
return ans;
}
int main()
{
int n = 10;
cout << sumDivisorsOfDivisors(n);
return 0;
}
Java
import java.util.HashMap;
class GFG
{
public static int sumDivisorsOfDivisors(int n)
{
HashMap<Integer, Integer> mp = new HashMap<>();
for (int j = 2; j <= Math.sqrt(n); j++)
{
int count = 0;
while (n % j == 0)
{
n /= j;
count++;
}
if (count != 0)
mp.put(j, count);
}
if (n != 1)
mp.put(n, 1);
int ans = 1;
for (HashMap.Entry<Integer, Integer> entry : mp.entrySet())
{
int pw = 1;
int sum = 0;
for (int i = entry.getValue() + 1; i >= 1; i--)
{
sum += (i * pw);
pw *= entry.getKey();
}
ans *= sum;
}
return ans;
}
public static void main(String[] args)
{
int n = 10;
System.out.println(sumDivisorsOfDivisors(n));
}
}
Python3
import math as mt
def sumDivisorsOfDivisors(n):
mp = dict()
for j in range(2, mt.ceil(mt.sqrt(n))):
count = 0
while (n % j == 0):
n //= j
count += 1
if (count):
mp[j] = count
if (n != 1):
mp[n] = 1
ans = 1
for it in mp:
pw = 1
summ = 0
for i in range(mp[it] + 1, 0, -1):
summ += (i * pw)
pw *= it
ans *= summ
return ans
n = 10
print(sumDivisorsOfDivisors(n))
C#
using System;
using System.Collections.Generic;
class GFG
{
public static int sumDivisorsOfDivisors(int n)
{
Dictionary<int,
int> mp = new Dictionary<int,
int>();
for (int j = 2; j <= Math.Sqrt(n); j++)
{
int count = 0;
while (n % j == 0)
{
n /= j;
count++;
}
if (count != 0)
mp.Add(j, count);
}
if (n != 1)
mp.Add(n, 1);
int ans = 1;
foreach(KeyValuePair<int, int> entry in mp)
{
int pw = 1;
int sum = 0;
for (int i = entry.Value + 1;
i >= 1; i--)
{
sum += (i * pw);
pw = entry.Key;
}
ans *= sum;
}
return ans;
}
public static void Main(String[] args)
{
int n = 10;
Console.WriteLine(sumDivisorsOfDivisors(n));
}
}
Javascript
<script>
function sumDivisorsOfDivisors(n)
{
let mp = new Map();
for (let j = 2; j <= Math.sqrt(n); j++)
{
let count = 0;
while (n % j == 0)
{
n = Math.floor(n/j);
count++;
}
if (count != 0)
mp.set(j, count);
}
if (n != 1)
mp.set(n, 1);
let ans = 1;
for (let [key, value] of mp.entries())
{
let pw = 1;
let sum = 0;
for (let i = value + 1; i >= 1; i--)
{
sum += (i * pw);
pw = key;
}
ans *= sum;
}
return ans;
}
let n = 10;
document.write(sumDivisorsOfDivisors(n));
</script>
Output:
28
Time Complexity: O(√n log n)
Auxiliary Space: O(n)
Optimizations :
For the cases when there are multiple inputs for which we need find the value, we can use Sieve of Eratosthenes as discussed in this post.
This article is contributed by Aarti_Rathi and Anuj Chauhan. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
23 Jun, 2022
Like Article
Save Article
Сумма делителей числа
Сумма делителей числа.
Для
начало приведём экспериментальный материал (который был получен с помощью
программы Derive (по формуле 1.(см.ниже)): для нахождения делителей числа «a»,
программа делила число «a» на другие числа не превосходящие само число и если
остаток от деления был равен 0, то число записывалось как делитель «a». ):
Ниже приведены все делители
чисел от 1 до 1000:
[1, [1]]
[2, [1, 2]]
[3, [1, 3]]
[4, [1, 2, 4]]
[5, [1, 5]]
[6, [1, 2, 3, 6]]
[7, [1, 7]]
[8, [1, 2, 4, 8]]
[9, [1, 3, 9]]
[10, [1, 2, 5, 10]]
[11, [1, 11]]
[12, [1, 2, 3, 4, 6, 12]]
[13, [1, 13]]
[14, [1, 2, 7, 14]]
[15, [1, 3, 5, 15]]
[16, [1, 2, 4, 8, 16]]
[17, [1, 17]]
[18, [1, 2, 3, 6, 9, 18]]
[19, [1, 19]]
[20, [1, 2, 4, 5, 10, 20]]
[21, [1, 3, 7, 21]]
[22, [1, 2, 11, 22]]
[23, [1, 23]]
[24, [1, 2, 3, 4, 6, 8, 12, 24]]
[25, [1, 5, 25]]
[26, [1, 2, 13, 26]]
[27, [1, 3, 9, 27]]
[28, [1, 2, 4, 7, 14, 28]]
[29, [1, 29]]
[30, [1, 2, 3, 5, 6, 10, 15, 30]]
[31, [1, 31]]
[32, [1, 2, 4, 8, 16, 32]]
[33, [1, 3, 11, 33]]
[34, [1, 2, 17, 34]]
[35, [1, 5, 7, 35]]
[36, [1, 2, 3, 4, 6, 9, 12, 18, 36]]
[37, [1, 37]]
[38, [1, 2, 19, 38]]
[39, [1, 3, 13, 39]]
[40, [1, 2, 4, 5, 8, 10, 20, 40]]
[41, [1, 41]]
[42, [1, 2, 3, 6, 7, 14, 21, 42]]
[43, [1, 43]]
[44, [1, 2, 4, 11, 22, 44]]
[45, [1, 3, 5, 9, 15, 45]]
[46, [1, 2, 23, 46]]
[47, [1, 47]]
[48, [1, 2, 3, 4, 6, 8, 12, 16, 24, 48]]
[49, [1, 7, 49]]
[50, [1, 2, 5, 10, 25, 50]]
[51, [1, 3, 17, 51]]
[52, [1, 2, 4, 13, 26, 52]]
[53, [1, 53]]
[54, [1, 2, 3, 6, 9, 18, 27, 54]]
[55, [1, 5, 11, 55]]
[56, [1, 2, 4, 7, 8, 14, 28, 56]]
[57, [1, 3, 19, 57]]
[58, [1, 2, 29, 58]]
[59, [1, 59]]
[60, [1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60]]
[61, [1, 61]]
[62, [1, 2, 31, 62]]
[63, [1, 3, 7, 9, 21, 63]]
[64, [1, 2, 4, 8, 16, 32, 64]]
[65, [1, 5, 13, 65]]
[66, [1, 2, 3, 6, 11, 22, 33, 66]]
[67, [1, 67]]
[68, [1, 2, 4, 17, 34, 68]]
[69, [1, 3, 23, 69]]
[70, [1, 2, 5, 7, 10, 14, 35, 70]]
[71, [1, 71]]
[72, [1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72]]
[73, [1, 73]]
[74, [1, 2, 37, 74]]
[75, [1, 3, 5, 15, 25, 75]]
[76, [1, 2, 4, 19, 38, 76]]
[77, [1, 7, 11, 77]]
[78, [1, 2, 3, 6, 13, 26, 39, 78]]
[79, [1, 79]]
[80, [1, 2, 4, 5, 8, 10, 16, 20, 40, 80]]
[81, [1, 3, 9, 27, 81]]
[82, [1, 2, 41, 82]]
[83, [1, 83]]
[84, [1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84]]
[85, [1, 5, 17, 85]]
[86, [1, 2, 43, 86]]
[87, [1, 3, 29, 87]]
[88, [1, 2, 4, 8, 11, 22, 44, 88]]
[89, [1, 89]]
[90, [1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90]]
[91, [1, 7, 13, 91]]
[92, [1, 2, 4, 23, 46, 92]]
[93, [1, 3, 31, 93]]
[94, [1, 2, 47, 94]]
[95, [1, 5, 19, 95]]
[96, [1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96]]
[97, [1, 97]]
[98, [1, 2, 7, 14, 49, 98]]
[99, [1, 3, 9, 11, 33, 99]]
[100, [1, 2, 4, 5, 10, 20, 25, 50, 100]]
[101, [1, 101]]
[102, [1, 2, 3, 6, 17, 34, 51, 102]]
[103, [1, 103]]
[104, [1, 2, 4, 8, 13, 26, 52, 104]]
[105, [1, 3, 5, 7, 15, 21, 35, 105]]
[106, [1, 2, 53, 106]]
[107, [1, 107]]
[108, [1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108]]
[109, [1, 109]]
[110, [1, 2, 5, 10, 11, 22, 55, 110]]
[111, [1, 3, 37, 111]]
[112, [1, 2, 4, 7, 8, 14, 16, 28, 56, 112]]
[113, [1, 113]]
[114, [1, 2, 3, 6, 19, 38, 57, 114]]
[115, [1, 5, 23, 115]]
[116, [1, 2, 4, 29, 58, 116]]
[117, [1, 3, 9, 13, 39, 117]]
[118, [1, 2, 59, 118]]
[119, [1, 7, 17, 119]]
[120, [1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60,
120]]
[121, [1, 11, 121]]
[122, [1, 2, 61, 122]]
[123, [1, 3, 41, 123]]
[124, [1, 2, 4, 31, 62, 124]]
[125, [1, 5, 25, 125]]
[126, [1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126]]
[127, [1, 127]]
[128, [1, 2, 4, 8, 16, 32, 64, 128]]
[129, [1, 3, 43, 129]]
[130, [1, 2, 5, 10, 13, 26, 65, 130]]
[131, [1, 131]]
[132, [1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132]]
[133, [1, 7, 19, 133]]
[134, [1, 2, 67, 134]]
[135, [1, 3, 5, 9, 15, 27, 45, 135]]
[136, [1, 2, 4, 8, 17, 34, 68, 136]]
[137, [1, 137]]
[138, [1, 2, 3, 6, 23, 46, 69, 138]]
[139, [1, 139]]
[140, [1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140]]
[141, [1, 3, 47, 141]]
[142, [1, 2, 71, 142]]
[143, [1, 11, 13, 143]]
[144, [1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72,
144]]
[145, [1, 5, 29, 145]]
[146, [1, 2, 73, 146]]
[147, [1, 3, 7, 21, 49, 147]]
[148, [1, 2, 4, 37, 74, 148]]
[149, [1, 149]]
[150, [1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150]]
[151, [1, 151]]
[152, [1, 2, 4, 8, 19, 38, 76, 152]]
[153, [1, 3, 9, 17, 51, 153]]
[154, [1, 2, 7, 11, 14, 22, 77, 154]]
[155, [1, 5, 31, 155]]
[156, [1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78, 156]]
[157, [1, 157]]
[158, [1, 2, 79, 158]]
[159, [1, 3, 53, 159]]
[160, [1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, 160]]
[161, [1, 7, 23, 161]]
[162, [1, 2, 3, 6, 9, 18, 27, 54, 81, 162]]
[163, [1, 163]]
[164, [1, 2, 4, 41, 82, 164]]
[165, [1, 3, 5, 11, 15, 33, 55, 165]]
[166, [1, 2, 83, 166]]
[167, [1, 167]]
[168, [1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84,
168]]
[169, [1, 13, 169]]
[170, [1, 2, 5, 10, 17, 34, 85, 170]]
[171, [1, 3, 9, 19, 57, 171]]
[172, [1, 2, 4, 43, 86, 172]]
[173, [1, 173]]
[174, [1, 2, 3, 6, 29, 58, 87, 174]]
[175, [1, 5, 7, 25, 35, 175]]
[176, [1, 2, 4, 8, 11, 16, 22, 44, 88, 176]]
[177, [1, 3, 59, 177]]
[178, [1, 2, 89, 178]]
[179, [1, 179]]
[180, [1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45,
60, 90, 180]]
[181, [1, 181]]
[182, [1, 2, 7, 13, 14, 26, 91, 182]]
[183, [1, 3, 61, 183]]
[184, [1, 2, 4, 8, 23, 46, 92, 184]]
[185, [1, 5, 37, 185]]
[186, [1, 2, 3, 6, 31, 62, 93, 186]]
[187, [1, 11, 17, 187]]
[188, [1, 2, 4, 47, 94, 188]]
[189, [1, 3, 7, 9, 21, 27, 63, 189]]
[190, [1, 2, 5, 10, 19, 38, 95, 190]]
[191, [1, 191]]
[192, [1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192]]
[193, [1, 193]]
[194, [1, 2, 97, 194]]
[195, [1, 3, 5, 13, 15, 39, 65, 195]]
[196, [1, 2, 4, 7, 14, 28, 49, 98, 196]]
[197, [1, 197]]
[198, [1, 2, 3, 6, 9, 11, 18, 22, 33, 66, 99, 198]]
[199, [1, 199]]
[200, [1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200]]
[201, [1, 3, 67, 201]]
[202, [1, 2, 101, 202]]
[203, [1, 7, 29, 203]]
[204, [1, 2, 3, 4, 6, 12, 17, 34, 51, 68, 102, 204]]
[205, [1, 5, 41, 205]]
[206, [1, 2, 103, 206]]
[207, [1, 3, 9, 23, 69, 207]]
[208, [1, 2, 4, 8, 13, 16, 26, 52, 104, 208]]
[209, [1, 11, 19, 209]]
[210, [1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70,
105, 210]]
[211, [1, 211]]
[212, [1, 2, 4, 53, 106, 212]]
[213, [1, 3, 71, 213]]
[214, [1, 2, 107, 214]]
[215, [1, 5, 43, 215]]
[216, [1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108,
216]]
[217, [1, 7, 31, 217]]
[218, [1, 2, 109, 218]]
[219, [1, 3, 73, 219]]
[220, [1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220]]
[221, [1, 13, 17, 221]]
[222, [1, 2, 3, 6, 37, 74, 111, 222]]
[223, [1, 223]]
[224, [1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224]]
[225, [1, 3, 5, 9, 15, 25, 45, 75, 225]]
[226, [1, 2, 113, 226]]
[227, [1, 227]]
[228, [1, 2, 3, 4, 6, 12, 19, 38, 57, 76, 114, 228]]
[229, [1, 229]]
[230, [1, 2, 5, 10, 23, 46, 115, 230]]
[231, [1, 3, 7, 11, 21, 33, 77, 231]]
[232, [1, 2, 4, 8, 29, 58, 116, 232]]
[233, [1, 233]]
[234, [1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117, 234]]
[235, [1, 5, 47, 235]]
[236, [1, 2, 4, 59, 118, 236]]
[237, [1, 3, 79, 237]]
[238, [1, 2, 7, 14, 17, 34, 119, 238]]
[239, [1, 239]]
[240, [1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40,
48, 60, 80, 120, 240]]
[241, [1, 241]]
[242, [1, 2, 11, 22, 121, 242]]
[243, [1, 3, 9, 27, 81, 243]]
[244, [1, 2, 4, 61, 122, 244]]
[245, [1, 5, 7, 35, 49, 245]]
[246, [1, 2, 3, 6, 41, 82, 123, 246]]
[247, [1, 13, 19, 247]]
[248, [1, 2, 4, 8, 31, 62, 124, 248]]
[249, [1, 3, 83, 249]]
[250, [1, 2, 5, 10, 25, 50, 125, 250]]
[251, [1, 251]]
[252, [1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63,
84, 126, 252]]
[253, [1, 11, 23, 253]]
[254, [1, 2, 127, 254]]
[255, [1, 3, 5, 15, 17, 51, 85, 255]]
[256, [1, 2, 4, 8, 16, 32, 64, 128, 256]]
[257, [1, 257]]
[258, [1, 2, 3, 6, 43, 86, 129, 258]]
[259, [1, 7, 37, 259]]
[260, [1, 2, 4, 5, 10, 13, 20, 26, 52, 65, 130, 260]]
[261, [1, 3, 9, 29, 87, 261]]
[262, [1, 2, 131, 262]]
[263, [1, 263]]
[264, [1, 2, 3, 4, 6, 8, 11, 12, 22, 24, 33, 44, 66, 88,
132, 264]]
[265, [1, 5, 53, 265]]
[266, [1, 2, 7, 14, 19, 38, 133, 266]]
[267, [1, 3, 89, 267]]
[268, [1, 2, 4, 67, 134, 268]]
[269, [1, 269]]
[270, [1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90,
135, 270]]
[271, [1, 271]]
[272, [1, 2, 4, 8, 16, 17, 34, 68, 136, 272]]
[273, [1, 3, 7, 13, 21, 39, 91, 273]]
[274, [1, 2, 137, 274]]
[275, [1, 5, 11, 25, 55, 275]]
[276, [1, 2, 3, 4, 6, 12, 23, 46, 69, 92, 138, 276]]
[277, [1, 277]]
[278, [1, 2, 139, 278]]
[279, [1, 3, 9, 31, 93, 279]]
[280, [1, 2, 4, 5, 7, 8, 10, 14, 20, 28, 35, 40, 56, 70,
140, 280]]
[281, [1, 281]]
[282, [1, 2, 3, 6, 47, 94, 141, 282]]
[283, [1, 283]]
[284, [1, 2, 4, 71, 142, 284]]
[285, [1, 3, 5, 15, 19, 57, 95, 285]]
[286, [1, 2, 11, 13, 22, 26, 143, 286]]
[287, [1, 7, 41, 287]]
[288, [1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72,
96, 144, 288]]
[289, [1, 17, 289]]
[290, [1, 2, 5, 10, 29, 58, 145, 290]]
[291, [1, 3, 97, 291]]
[292, [1, 2, 4, 73, 146, 292]]
[293, [1, 293]]
[294, [1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, 294]]
[295, [1, 5, 59, 295]]
[296, [1, 2, 4, 8, 37, 74, 148, 296]]
[297, [1, 3, 9, 11, 27, 33, 99, 297]]
[298, [1, 2, 149, 298]]
[299, [1, 13, 23, 299]]
[300, [1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75,
100, 150, 300]]
[301, [1, 7, 43, 301]]
[302, [1, 2, 151, 302]]
[303, [1, 3, 101, 303]]
[304, [1, 2, 4, 8, 16, 19, 38, 76, 152, 304]]
[305, [1, 5, 61, 305]]
[306, [1, 2, 3, 6, 9, 17, 18, 34, 51, 102, 153, 306]]
[307, [1, 307]]
[308, [1, 2, 4, 7, 11, 14, 22, 28, 44, 77, 154, 308]]
[309, [1, 3, 103, 309]]
[310, [1, 2, 5, 10, 31, 62, 155, 310]]
[311, [1, 311]]
[312, [1, 2, 3, 4, 6, 8, 12, 13, 24, 26, 39, 52, 78, 104,
156, 312]]
[313, [1, 313]]
[314, [1, 2, 157, 314]]
[315, [1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, 315]]
[316, [1, 2, 4, 79, 158, 316]]
[317, [1, 317]]
[318, [1, 2, 3, 6, 53, 106, 159, 318]]
[319, [1, 11, 29, 319]]
[320, [1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, 320]]
[321, [1, 3, 107, 321]]
[322, [1, 2, 7, 14, 23, 46, 161, 322]]
[323, [1, 17, 19, 323]]
[324, [1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162,
324]]
[325, [1, 5, 13, 25, 65, 325]]
[326, [1, 2, 163, 326]]
[327, [1, 3, 109, 327]]
[328, [1, 2, 4, 8, 41, 82, 164, 328]]
[329, [1, 7, 47, 329]]
[330, [1, 2, 3, 5, 6, 10, 11, 15, 22, 30, 33, 55, 66, 110,
165, 330]]
[331, [1, 331]]
[332, [1, 2, 4, 83, 166, 332]]
[333, [1, 3, 9, 37, 111, 333]]
[334, [1, 2, 167, 334]]
[335, [1, 5, 67, 335]]
[336, [1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 42, 48,
56, 84, 112, 168, 336]]
[337, [1, 337]]
[338, [1, 2, 13, 26, 169, 338]]
[339, [1, 3, 113, 339]]
[340, [1, 2, 4, 5, 10, 17, 20, 34, 68, 85, 170, 340]]
[341, [1, 11, 31, 341]]
[342, [1, 2, 3, 6, 9, 18, 19, 38, 57, 114, 171, 342]]
[343, [1, 7, 49, 343]]
[344, [1, 2, 4, 8, 43, 86, 172, 344]]
[345, [1, 3, 5, 15, 23, 69, 115, 345]]
[346, [1, 2, 173, 346]]
[347, [1, 347]]
[349, [1, 349]]
[350, [1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350]]
[351, [1, 3, 9, 13, 27, 39, 117, 351]]
[352, [1, 2, 4, 8, 11, 16, 22, 32, 44, 88, 176, 352]]
[353, [1, 353]]
[354, [1, 2, 3, 6, 59, 118, 177, 354]]
[355, [1, 5, 71, 355]]
[356, [1, 2, 4, 89, 178, 356]]
[357, [1, 3, 7, 17, 21, 51, 119, 357]]
[358, [1, 2, 179, 358]]
[359, [1, 359]]
[360, [1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30,
36, 40, 45, 60, 72, 90, 120, 180, 360]]
[361, [1, 19, 361]]
[362, [1, 2, 181, 362]]
[363, [1, 3, 11, 33, 121, 363]]
[364, [1, 2, 4, 7, 13, 14, 26, 28, 52, 91, 182, 364]]
[365, [1, 5, 73, 365]]
[366, [1, 2, 3, 6, 61, 122, 183, 366]]
[367, [1, 367]]
[368, [1, 2, 4, 8, 16, 23, 46, 92, 184, 368]]
[369, [1, 3, 9, 41, 123, 369]]
[370, [1, 2, 5, 10, 37, 74, 185, 370]]
[371, [1, 7, 53, 371]]
[372, [1, 2, 3, 4, 6, 12, 31, 62, 93, 124, 186, 372]]
[373, [1, 373]]
[374, [1, 2, 11, 17, 22, 34, 187, 374]]
[375, [1, 3, 5, 15, 25, 75, 125, 375]]
[376, [1, 2, 4, 8, 47, 94, 188, 376]]
[377, [1, 13, 29, 377]]
[378, [1, 2, 3, 6, 7, 9, 14, 18, 21, 27, 42, 54, 63, 126,
189, 378]]
[379, [1, 379]]
[380, [1, 2, 4, 5, 10, 19, 20, 38, 76, 95, 190, 380]]
[381, [1, 3, 127, 381]]
[382, [1, 2, 191, 382]]
[383, [1, 383]]
[384, [1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128,
192, 384]]
[385, [1, 5, 7, 11, 35, 55, 77, 385]]
[386, [1, 2, 193, 386]]
[387, [1, 3, 9, 43, 129, 387]]
[388, [1, 2, 4, 97, 194, 388]]
[389, [1, 389]]
[390, [1, 2, 3, 5, 6, 10, 13, 15, 26, 30, 39, 65, 78, 130,
195, 390]]
[391, [1, 17, 23, 391]]
[392, [1, 2, 4, 7, 8, 14, 28, 49, 56, 98, 196, 392]]
[393, [1, 3, 131, 393]]
[394, [1, 2, 197, 394]]
[395, [1, 5, 79, 395]]
[396, [1, 2, 3, 4, 6, 9, 11, 12, 18, 22, 33, 36, 44, 66, 99,
132, 198, 396]]
[397, [1, 397]]
[398, [1, 2, 199, 398]]
[399, [1, 3, 7, 19, 21, 57, 133, 399]]
[400, [1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200,
400]]
[401, [1, 401]]
[402, [1, 2, 3, 6, 67, 134, 201, 402]]
[403, [1, 13, 31, 403]]
[404, [1, 2, 4, 101, 202, 404]]
[405, [1, 3, 5, 9, 15, 27, 45, 81, 135, 405]]
[406, [1, 2, 7, 14, 29, 58, 203, 406]]
[407, [1, 11, 37, 407]]
[408, [1, 2, 3, 4, 6, 8, 12, 17, 24, 34, 51, 68, 102, 136,
204, 408]]
[409, [1, 409]]
[410, [1, 2, 5, 10, 41, 82, 205, 410]]
[411, [1, 3, 137, 411]]
[412, [1, 2, 4, 103, 206, 412]]
[413, [1, 7, 59, 413]]
[414, [1, 2, 3, 6, 9, 18, 23, 46, 69, 138, 207, 414]]
[415, [1, 5, 83, 415]]
[416, [1, 2, 4, 8, 13, 16, 26, 32, 52, 104, 208, 416]]
[417, [1, 3, 139, 417]]
[418, [1, 2, 11, 19, 22, 38, 209, 418]]
[419, [1, 419]]
[420, [1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30,
35, 42, 60, 70, 84, 105, 140, 210, 420]]
[421, [1, 421]]
[422, [1, 2, 211, 422]]
[423, [1, 3, 9, 47, 141, 423]]
[424, [1, 2, 4, 8, 53, 106, 212, 424]]
[425, [1, 5, 17, 25, 85, 425]]
[426, [1, 2, 3, 6, 71, 142, 213, 426]]
[427, [1, 7, 61, 427]]
[428, [1, 2, 4, 107, 214, 428]]
[429, [1, 3, 11, 13, 33, 39, 143, 429]]
[430, [1, 2, 5, 10, 43, 86, 215, 430]]
[431, [1, 431]]
[432, [1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54,
72, 108, 144, 216, 432]]
[433, [1, 433]]
[434, [1, 2, 7, 14, 31, 62, 217, 434]]
[435, [1, 3, 5, 15, 29, 87, 145, 435]]
[436, [1, 2, 4, 109, 218, 436]]
[437, [1, 19, 23, 437]]
[438, [1, 2, 3, 6, 73, 146, 219, 438]]
[439, [1, 439]]
[440, [1, 2, 4, 5, 8, 10, 11, 20, 22, 40, 44, 55, 88, 110,
220, 440]]
[441, [1, 3, 7, 9, 21, 49, 63, 147, 441]]
[442, [1, 2, 13, 17, 26, 34, 221, 442]]
[443, [1, 443]]
[444, [1, 2, 3, 4, 6, 12, 37, 74, 111, 148, 222, 444]]
[445, [1, 5, 89, 445]]
[446, [1, 2, 223, 446]]
[447, [1, 3, 149, 447]]
[448, [1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 112, 224,
448]]
[449, [1, 449]]
[450, [1, 2, 3, 5, 6, 9, 10, 15, 18, 25, 30, 45, 50, 75, 90,
150, 225, 450]]
[451, [1, 11, 41, 451]]
[452, [1, 2, 4, 113, 226, 452]]
[453, [1, 3, 151, 453]]
[454, [1, 2, 227, 454]]
[455, [1, 5, 7, 13, 35, 65, 91, 455]]
[456, [1, 2, 3, 4, 6, 8, 12, 19, 24, 38, 57, 76, 114, 152,
228, 456]]
[457, [1, 457]]
[458, [1, 2, 229, 458]]
[459, [1, 3, 9, 17, 27, 51, 153, 459]]
[460, [1, 2, 4, 5, 10, 20, 23, 46, 92, 115, 230, 460]]
[461, [1, 461]]
[462, [1, 2, 3, 6, 7, 11, 14, 21, 22, 33, 42, 66, 77, 154,
231, 462]]
[463, [1, 463]]
[464, [1, 2, 4, 8, 16, 29, 58, 116, 232, 464]]
[465, [1, 3, 5, 15, 31, 93, 155, 465]]
[466, [1, 2, 233, 466]]
[467, [1, 467]]
[468, [1, 2, 3, 4, 6, 9, 12, 13, 18, 26, 36, 39, 52, 78,
117, 156, 234, 468]]
[469, [1, 7, 67, 469]]
[470, [1, 2, 5, 10, 47, 94, 235, 470]]
[471, [1, 3, 157, 471]]
[472, [1, 2, 4, 8, 59, 118, 236, 472]]
[473, [1, 11, 43, 473]]
[474, [1, 2, 3, 6, 79, 158, 237, 474]]
[475, [1, 5, 19, 25, 95, 475]]
[476, [1, 2, 4, 7, 14, 17, 28, 34, 68, 119, 238, 476]]
[477, [1, 3, 9, 53, 159, 477]]
[478, [1, 2, 239, 478]]
[479, [1, 479]]
[480, [1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32,
40, 48, 60, 80, 96, 120, 160, 240, 480]]
[481, [1, 13, 37, 481]]
[482, [1, 2, 241, 482]]
[483, [1, 3, 7, 21, 23, 69, 161, 483]]
[484, [1, 2, 4, 11, 22, 44, 121, 242, 484]]
[485, [1, 5, 97, 485]]
[486, [1, 2, 3, 6, 9, 18, 27, 54, 81, 162, 243, 486]]
[487, [1, 487]]
[488, [1, 2, 4, 8, 61, 122, 244, 488]]
[489, [1, 3, 163, 489]]
[490, [1, 2, 5, 7, 10, 14, 35, 49, 70, 98, 245, 490]]
[491, [1, 491]]
[492, [1, 2, 3, 4, 6, 12, 41, 82, 123, 164, 246, 492]]
[493, [1, 17, 29, 493]]
[494, [1, 2, 13, 19, 26, 38, 247, 494]]
[495, [1, 3, 5, 9, 11, 15, 33, 45, 55, 99, 165, 495]]
[496, [1, 2, 4, 8, 16, 31, 62, 124, 248, 496]]
[497, [1, 7, 71, 497]]
[498, [1, 2, 3, 6, 83, 166, 249, 498]]
[499, [1, 499]]
[500, [1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500]]
[501, [1, 3, 167, 501]]
[502, [1, 2, 251, 502]]
[503, [1, 503]]
[504, [1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 18, 21, 24, 28, 36,
42, 56, 63, 72, 84, 126, 168, 252, 504]]
[505, [1, 5, 101, 505]]
[506, [1, 2, 11, 22, 23, 46, 253, 506]]
[507, [1, 3, 13, 39, 169, 507]]
[508, [1, 2, 4, 127, 254, 508]]
[509, [1, 509]]
[510, [1, 2, 3, 5, 6, 10, 15, 17, 30, 34, 51, 85, 102, 170,
255, 510]]
[511, [1, 7, 73, 511]]
[512, [1, 2, 4, 8, 16, 32, 64, 128, 256, 512]]
[513, [1, 3, 9, 19, 27, 57, 171, 513]]
[514, [1, 2, 257, 514]]
[515, [1, 5, 103, 515]]
[516, [1, 2, 3, 4, 6, 12, 43, 86, 129, 172, 258, 516]]
[517, [1, 11, 47, 517]]
[518, [1, 2, 7, 14, 37, 74, 259, 518]]
[519, [1, 3, 173, 519]]
[520, [1, 2, 4, 5, 8, 10, 13, 20, 26, 40, 52, 65, 104, 130,
260, 520]]
[521, [1, 521]]
[522, [1, 2, 3, 6, 9, 18, 29, 58, 87, 174, 261, 522]]
[523, [1, 523]]
[524, [1, 2, 4, 131, 262, 524]]
[525, [1, 3, 5, 7, 15, 21, 25, 35, 75, 105, 175, 525]]
[526, [1, 2, 263, 526]]
[527, [1, 17, 31, 527]]
[528, [1, 2, 3, 4, 6, 8, 11, 12, 16, 22, 24, 33, 44, 48, 66,
88, 132, 176, 264, 528]]
[529, [1, 23, 529]]
[530, [1, 2, 5, 10, 53, 106, 265, 530]]
[531, [1, 3, 9, 59, 177, 531]]
[532, [1, 2, 4, 7, 14, 19, 28, 38, 76, 133, 266, 532]]
[533, [1, 13, 41, 533]]
[534, [1, 2, 3, 6, 89, 178, 267, 534]]
[535, [1, 5, 107, 535]]
[536, [1, 2, 4, 8, 67, 134, 268, 536]]
[537, [1, 3, 179, 537]]
[538, [1, 2, 269, 538]]
[539, [1, 7, 11, 49, 77, 539]]
[540, [1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36,
45, 54, 60, 90, 108, 135, 180, 270, 540]]
[541, [1, 541]]
[542, [1, 2, 271, 542]]
[543, [1, 3, 181, 543]]
[544, [1, 2, 4, 8, 16, 17, 32, 34, 68, 136, 272, 544]]
[545, [1, 5, 109, 545]]
[546, [1, 2, 3, 6, 7, 13, 14, 21, 26, 39, 42, 78, 91, 182,
273, 546]]
[547, [1, 547]]
[548, [1, 2, 4, 137, 274, 548]]
[549, [1, 3, 9, 61, 183, 549]]
[550, [1, 2, 5, 10, 11, 22, 25, 50, 55, 110, 275, 550]]
[551, [1, 19, 29, 551]]
[552, [1, 2, 3, 4, 6, 8, 12, 23, 24, 46, 69, 92, 138, 184,
276, 552]]
[553, [1, 7, 79, 553]]
[554, [1, 2, 277, 554]]
[555, [1, 3, 5, 15, 37, 111, 185, 555]]
[556, [1, 2, 4, 139, 278, 556]]
[557, [1, 557]]
[558, [1, 2, 3, 6, 9, 18, 31, 62, 93, 186, 279, 558]]
[559, [1, 13, 43, 559]]
[560, [1, 2, 4, 5, 7, 8, 10, 14, 16, 20, 28, 35, 40, 56, 70,
80, 112, 140, 280, 560]]
[561, [1, 3, 11, 17, 33, 51, 187, 561]]
[562, [1, 2, 281, 562]]
[563, [1, 563]]
[564, [1, 2, 3, 4, 6, 12, 47, 94, 141, 188, 282, 564]]
[565, [1, 5, 113, 565]]
[566, [1, 2, 283, 566]]
[567, [1, 3, 7, 9, 21, 27, 63, 81, 189, 567]]
[568, [1, 2, 4, 8, 71, 142, 284, 568]]
[569, [1, 569]]
[570, [1, 2, 3, 5, 6, 10, 15, 19, 30, 38, 57, 95, 114, 190,
285, 570]]
[571, [1, 571]]
[572, [1, 2, 4, 11, 13, 22, 26, 44, 52, 143, 286, 572]]
[573, [1, 3, 191, 573]]
[574, [1, 2, 7, 14, 41, 82, 287, 574]]
[575, [1, 5, 23, 25, 115, 575]]
[576, [1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64,
72, 96, 144, 192, 288, 576]]
[577, [1, 577]]
[578, [1, 2, 17, 34, 289, 578]]
[579, [1, 3, 193, 579]]
[580, [1, 2, 4, 5, 10, 20, 29, 58, 116, 145, 290, 580]]
[581, [1, 7, 83, 581]]
[582, [1, 2, 3, 6, 97, 194, 291, 582]]
[583, [1, 11, 53, 583]]
[584, [1, 2, 4, 8, 73, 146, 292, 584]]
[585, [1, 3, 5, 9, 13, 15, 39, 45, 65, 117, 195, 585]]
[586, [1, 2, 293, 586]]
[587, [1, 587]]
[588, [1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 49, 84, 98,
147, 196, 294, 588]]
[589, [1, 19, 31, 589]]
[590, [1, 2, 5, 10, 59, 118, 295, 590]]
[591, [1, 3, 197, 591]]
[592, [1, 2, 4, 8, 16, 37, 74, 148, 296, 592]]
[593, [1, 593]]
[594, [1, 2, 3, 6, 9, 11, 18, 22, 27, 33, 54, 66, 99, 198,
297, 594]]
[595, [1, 5, 7, 17, 35, 85, 119, 595]]
[596, [1, 2, 4, 149, 298, 596]]
[597, [1, 3, 199, 597]]
[598, [1, 2, 13, 23, 26, 46, 299, 598]]
[599, [1, 599]]
[600, [1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40,
50, 60, 75, 100, 120, 150, 200, 300, 600]]
[601, [1, 601]]
[602, [1, 2, 7, 14, 43, 86, 301, 602]]
[603, [1, 3, 9, 67, 201, 603]]
[604, [1, 2, 4, 151, 302, 604]]
[605, [1, 5, 11, 55, 121, 605]]
[606, [1, 2, 3, 6, 101, 202, 303, 606]]
[607, [1, 607]]
[608, [1, 2, 4, 8, 16, 19, 32, 38, 76, 152, 304, 608]]
[609, [1, 3, 7, 21, 29, 87, 203, 609]]
[610, [1, 2, 5, 10, 61, 122, 305, 610]]
[611, [1, 13, 47, 611]]
[612, [1, 2, 3, 4, 6, 9, 12, 17, 18, 34, 36, 51, 68, 102,
153, 204, 306, 612]]
[613, [1, 613]]
[614, [1, 2, 307, 614]]
[615, [1, 3, 5, 15, 41, 123, 205, 615]]
[616, [1, 2, 4, 7, 8, 11, 14, 22, 28, 44, 56, 77, 88, 154,
308, 616]]
[617, [1, 617]]
[618, [1, 2, 3, 6, 103, 206, 309, 618]]
[619, [1, 619]]
[620, [1, 2, 4, 5, 10, 20, 31, 62, 124, 155, 310, 620]]
[621, [1, 3, 9, 23, 27, 69, 207, 621]]
[622, [1, 2, 311, 622]]
[623, [1, 7, 89, 623]]
[624, [1, 2, 3, 4, 6, 8, 12, 13, 16, 24, 26, 39, 48, 52, 78,
104, 156, 208, 312, 624]]
[625, [1, 5, 25, 125, 625]]
[626, [1, 2, 313, 626]]
[627, [1, 3, 11, 19, 33, 57, 209, 627]]
[628, [1, 2, 4, 157, 314, 628]]
[629, [1, 17, 37, 629]]
[630, [1, 2, 3, 5, 6, 7, 9, 10, 14, 15, 18, 21, 30, 35, 42,
45, 63, 70, 90, 105, 126, 210, 315, 630]]
[631, [1, 631]]
[632, [1, 2, 4, 8, 79, 158, 316, 632]]
[633, [1, 3, 211, 633]]
[634, [1, 2, 317, 634]]
[635, [1, 5, 127, 635]]
[636, [1, 2, 3, 4, 6, 12, 53, 106, 159, 212, 318, 636]]
[637, [1, 7, 13, 49, 91, 637]]
[638, [1, 2, 11, 22, 29, 58, 319, 638]]
[639, [1, 3, 9, 71, 213, 639]]
[640, [1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 128, 160,
320, 640]]
[641, [1, 641]]
[642, [1, 2, 3, 6, 107, 214, 321, 642]]
[643, [1, 643]]
[644, [1, 2, 4, 7, 14, 23, 28, 46, 92, 161, 322, 644]]
[645, [1, 3, 5, 15, 43, 129, 215, 645]]
[646, [1, 2, 17, 19, 34, 38, 323, 646]]
[647, [1, 647]]
[648, [1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 81,
108, 162, 216, 324, 648]]
[649, [1, 11, 59, 649]]
[650, [1, 2, 5, 10, 13, 25, 26, 50, 65, 130, 325, 650]]
[651, [1, 3, 7, 21, 31, 93, 217, 651]]
[652, [1, 2, 4, 163, 326, 652]]
[653, [1, 653]]
[654, [1, 2, 3, 6, 109, 218, 327, 654]]
[655, [1, 5, 131, 655]]
[656, [1, 2, 4, 8, 16, 41, 82, 164, 328, 656]]
[657, [1, 3, 9, 73, 219, 657]]
[658, [1, 2, 7, 14, 47, 94, 329, 658]]
[659, [1, 659]]
[660, [1, 2, 3, 4, 5, 6, 10, 11, 12, 15, 20, 22, 30, 33, 44,
55, 60, 66, 110, 132, 165, 220, 330, 660]]
[661, [1, 661]]
[662, [1, 2, 331, 662]]
[663, [1, 3, 13, 17, 39, 51, 221, 663]]
[664, [1, 2, 4, 8, 83, 166, 332, 664]]
[665, [1, 5, 7, 19, 35, 95, 133, 665]]
[666, [1, 2, 3, 6, 9, 18, 37, 74, 111, 222, 333, 666]]
[667, [1, 23, 29, 667]]
[668, [1, 2, 4, 167, 334, 668]]
[669, [1, 3, 223, 669]]
[670, [1, 2, 5, 10, 67, 134, 335, 670]]
[671, [1, 11, 61, 671]]
[672, [1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 32, 42,
48, 56, 84, 96, 112, 168, 224, 336, 672]]
[673, [1, 673]]
[674, [1, 2, 337, 674]]
[675, [1, 3, 5, 9, 15, 25, 27, 45, 75, 135, 225, 675]]
[676, [1, 2, 4, 13, 26, 52, 169, 338, 676]]
[677, [1, 677]]
[678, [1, 2, 3, 6, 113, 226, 339, 678]]
[679, [1, 7, 97, 679]]
[680, [1, 2, 4, 5, 8, 10, 17, 20, 34, 40, 68, 85, 136, 170,
340, 680]]
[681, [1, 3, 227, 681]]
[682, [1, 2, 11, 22, 31, 62, 341, 682]]
[683, [1, 683]]
[684, [1, 2, 3, 4, 6, 9, 12, 18, 19, 36, 38, 57, 76, 114,
171, 228, 342, 684]]
[685, [1, 5, 137, 685]]
[686, [1, 2, 7, 14, 49, 98, 343, 686]]
[687, [1, 3, 229, 687]]
[688, [1, 2, 4, 8, 16, 43, 86, 172, 344, 688]]
[689, [1, 13, 53, 689]]
[690, [1, 2, 3, 5, 6, 10, 15, 23, 30, 46, 69, 115, 138, 230,
345, 690]]
[691, [1, 691]]
[692, [1, 2, 4, 173, 346, 692]]
[693, [1, 3, 7, 9, 11, 21, 33, 63, 77, 99, 231, 693]]
[694, [1, 2, 347, 694]]
[695, [1, 5, 139, 695]]
[696, [1, 2, 3, 4, 6, 8, 12, 24, 29, 58, 87, 116, 174, 232,
348, 696]]
[697, [1, 17, 41, 697]]
[698, [1, 2, 349, 698]]
[700, [1, 2, 4, 5, 7, 10, 14, 20, 25, 28, 35, 50, 70, 100,
140, 175, 350, 700]]
[701, [1, 701]]
[702, [1, 2, 3, 6, 9, 13, 18, 26, 27, 39, 54, 78, 117, 234,
351, 702]]
[703, [1, 19, 37, 703]]
[704, [1, 2, 4, 8, 11, 16, 22, 32, 44, 64, 88, 176, 352,
704]]
[705, [1, 3, 5, 15, 47, 141, 235, 705]]
[706, [1, 2, 353, 706]]
[707, [1, 7, 101, 707]]
[708, [1, 2, 3, 4, 6, 12, 59, 118, 177, 236, 354, 708]]
[709, [1, 709]]
[710, [1, 2, 5, 10, 71, 142, 355, 710]]
[711, [1, 3, 9, 79, 237, 711]]
[712, [1, 2, 4, 8, 89, 178, 356, 712]]
[713, [1, 23, 31, 713]]
[714, [1, 2, 3, 6, 7, 14, 17, 21, 34, 42, 51, 102, 119, 238,
357, 714]]
[715, [1, 5, 11, 13, 55, 65, 143, 715]]
[716, [1, 2, 4, 179, 358, 716]]
[717, [1, 3, 239, 717]]
[718, [1, 2, 359, 718]]
[719, [1, 719]]
[720, [1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24,
30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360, 720]]
[721, [1, 7, 103, 721]]
[722, [1, 2, 19, 38, 361, 722]]
[723, [1, 3, 241, 723]]
[724, [1, 2, 4, 181, 362, 724]]
[725, [1, 5, 25, 29, 145, 725]]
[726, [1, 2, 3, 6, 11, 22, 33, 66, 121, 242, 363, 726]]
[727, [1, 727]]
[728, [1, 2, 4, 7, 8, 13, 14, 26, 28, 52, 56, 91, 104, 182,
364, 728]]
[729, [1, 3, 9, 27, 81, 243, 729]]
[730, [1, 2, 5, 10, 73, 146, 365, 730]]
[731, [1, 17, 43, 731]]
[732, [1, 2, 3, 4, 6, 12, 61, 122, 183, 244, 366, 732]]
[733, [1, 733]]
[734, [1, 2, 367, 734]]
[735, [1, 3, 5, 7, 15, 21, 35, 49, 105, 147, 245, 735]]
[736, [1, 2, 4, 8, 16, 23, 32, 46, 92, 184, 368, 736]]
[737, [1, 11, 67, 737]]
[738, [1, 2, 3, 6, 9, 18, 41, 82, 123, 246, 369, 738]]
[739, [1, 739]]
[740, [1, 2, 4, 5, 10, 20, 37, 74, 148, 185, 370, 740]]
[741, [1, 3, 13, 19, 39, 57, 247, 741]]
[742, [1, 2, 7, 14, 53, 106, 371, 742]]
[743, [1, 743]]
[744, [1, 2, 3, 4, 6, 8, 12, 24, 31, 62, 93, 124, 186, 248,
372, 744]]
[745, [1, 5, 149, 745]]
[746, [1, 2, 373, 746]]
[747, [1, 3, 9, 83, 249, 747]]
[748, [1, 2, 4, 11, 17, 22, 34, 44, 68, 187, 374, 748]]
[749, [1, 7, 107, 749]]
[750, [1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 125, 150, 250,
375, 750]]
[751, [1, 751]]
[752, [1, 2, 4, 8, 16, 47, 94, 188, 376, 752]]
[753, [1, 3, 251, 753]]
[754, [1, 2, 13, 26, 29, 58, 377, 754]]
[755, [1, 5, 151, 755]]
[756, [1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 27, 28, 36, 42,
54, 63, 84, 108, 126, 189, 252, 378, 756]]
[757, [1, 757]]
[758, [1, 2, 379, 758]]
[759, [1, 3, 11, 23, 33, 69, 253, 759]]
[760, [1, 2, 4, 5, 8, 10, 19, 20, 38, 40, 76, 95, 152, 190,
380, 760]]
[761, [1, 761]]
[762, [1, 2, 3, 6, 127, 254, 381, 762]]
[763, [1, 7, 109, 763]]
[764, [1, 2, 4, 191, 382, 764]]
[765, [1, 3, 5, 9, 15, 17, 45, 51, 85, 153, 255, 765]]
[766, [1, 2, 383, 766]]
[767, [1, 13, 59, 767]]
[768, [1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128,
192, 256, 384, 768]]
[769, [1, 769]]
[770, [1, 2, 5, 7, 10, 11, 14, 22, 35, 55, 70, 77, 110, 154,
385, 770]]
[771, [1, 3, 257, 771]]
[772, [1, 2, 4, 193, 386, 772]]
[773, [1, 773]]
[774, [1, 2, 3, 6, 9, 18, 43, 86, 129, 258, 387, 774]]
[775, [1, 5, 25, 31, 155, 775]]
[776, [1, 2, 4, 8, 97, 194, 388, 776]]
[777, [1, 3, 7, 21, 37, 111, 259, 777]]
[778, [1, 2, 389, 778]]
[779, [1, 19, 41, 779]]
[780, [1, 2, 3, 4, 5, 6, 10, 12, 13, 15, 20, 26, 30, 39, 52,
60, 65, 78, 130, 156, 195, 260, 390, 780]]
[781, [1, 11, 71, 781]]
[782, [1, 2, 17, 23, 34, 46, 391, 782]]
[783, [1, 3, 9, 27, 29, 87, 261, 783]]
[784, [1, 2, 4, 7, 8, 14, 16, 28, 49, 56, 98, 112, 196, 392,
784]]
[785, [1, 5, 157, 785]]
[786, [1, 2, 3, 6, 131, 262, 393, 786]]
[787, [1, 787]]
[788, [1, 2, 4, 197, 394, 788]]
[789, [1, 3, 263, 789]]
[790, [1, 2, 5, 10, 79, 158, 395, 790]]
[791, [1, 7, 113, 791]]
[792, [1, 2, 3, 4, 6, 8, 9, 11, 12, 18, 22, 24, 33, 36, 44,
66, 72, 88, 99, 132, 198, 264, 396, 792]]
[793, [1, 13, 61, 793]]
[794, [1, 2, 397, 794]]
[795, [1, 3, 5, 15, 53, 159, 265, 795]]
[796, [1, 2, 4, 199, 398, 796]]
[797, [1, 797]]
[798, [1, 2, 3, 6, 7, 14, 19, 21, 38, 42, 57, 114, 133, 266,
399, 798]]
[799, [1, 17, 47, 799]]
[800, [1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 80, 100,
160, 200, 400, 800]]
[801, [1, 3, 9, 89, 267, 801]]
[802, [1, 2, 401, 802]]
[803, [1, 11, 73, 803]]
[804, [1, 2, 3, 4, 6, 12, 67, 134, 201, 268, 402, 804]]
[805, [1, 5, 7, 23, 35, 115, 161, 805]]
[806, [1, 2, 13, 26, 31, 62, 403, 806]]
[807, [1, 3, 269, 807]]
[808, [1, 2, 4, 8, 101, 202, 404, 808]]
[809, [1, 809]]
[810, [1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 81, 90,
135, 162, 270, 405, 810]]
[811, [1, 811]]
[812, [1, 2, 4, 7, 14, 28, 29, 58, 116, 203, 406, 812]]
[813, [1, 3, 271, 813]]
[814, [1, 2, 11, 22, 37, 74, 407, 814]]
[815, [1, 5, 163, 815]]
[816, [1, 2, 3, 4, 6, 8, 12, 16, 17, 24, 34, 48, 51, 68,
102, 136, 204, 272, 408, 816]]
[817, [1, 19, 43, 817]]
[818, [1, 2, 409, 818]]
[819, [1, 3, 7, 9, 13, 21, 39, 63, 91, 117, 273, 819]]
[820, [1, 2, 4, 5, 10, 20, 41, 82, 164, 205, 410, 820]]
[821, [1, 821]]
[822, [1, 2, 3, 6, 137, 274, 411, 822]]
[823, [1, 823]]
[824, [1, 2, 4, 8, 103, 206, 412, 824]]
[825, [1, 3, 5, 11, 15, 25, 33, 55, 75, 165, 275, 825]]
[826, [1, 2, 7, 14, 59, 118, 413, 826]]
[827, [1, 827]]
[828, [1, 2, 3, 4, 6, 9, 12, 18, 23, 36, 46, 69, 92, 138,
207, 276, 414, 828]]
[829, [1, 829]]
[830, [1, 2, 5, 10, 83, 166, 415, 830]]
[831, [1, 3, 277, 831]]
[832, [1, 2, 4, 8, 13, 16, 26, 32, 52, 64, 104, 208, 416,
832]]
[833, [1, 7, 17, 49, 119, 833]]
[834, [1, 2, 3, 6, 139, 278, 417, 834]]
[835, [1, 5, 167, 835]]
[836, [1, 2, 4, 11, 19, 22, 38, 44, 76, 209, 418, 836]]
[837, [1, 3, 9, 27, 31, 93, 279, 837]]
[838, [1, 2, 419, 838]]
[839, [1, 839]]
[840, [1, 2, 3, 4, 5, 6, 7, 8, 10,
12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70, 84, 105, 120, 140, 168,
210, 280, 420, 840]]
[841, [1, 29, 841]]
[842, [1, 2, 421, 842]]
[843, [1, 3, 281, 843]]
[844, [1, 2, 4, 211, 422, 844]]
[845, [1, 5, 13, 65, 169, 845]]
[846, [1, 2, 3, 6, 9, 18, 47, 94, 141, 282, 423, 846]]
[847, [1, 7, 11, 77, 121, 847]]
[848, [1, 2, 4, 8, 16, 53, 106, 212, 424, 848]]
[849, [1, 3, 283, 849]]
[850, [1, 2, 5, 10, 17, 25, 34, 50, 85, 170, 425, 850]]
[851, [1, 23, 37, 851]]
[852, [1, 2, 3, 4, 6, 12, 71, 142, 213, 284, 426, 852]]
[853, [1, 853]]
[854, [1, 2, 7, 14, 61, 122, 427, 854]]
[855, [1, 3, 5, 9, 15, 19, 45, 57, 95, 171, 285, 855]]
[856, [1, 2, 4, 8, 107, 214, 428, 856]]
[857, [1, 857]]
[858, [1, 2, 3, 6, 11, 13, 22, 26, 33, 39, 66, 78, 143, 286,
429, 858]]
[859, [1, 859]]
[860, [1, 2, 4, 5, 10, 20, 43, 86, 172, 215, 430, 860]]
[861, [1, 3, 7, 21, 41, 123, 287, 861]]
[862, [1, 2, 431, 862]]
[863, [1, 863]]
[864, [1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48,
54, 72, 96, 108, 144, 216, 288, 432, 864]]
[865, [1, 5, 173, 865]]
[866, [1, 2, 433, 866]]
[867, [1, 3, 17, 51, 289, 867]]
[868, [1, 2, 4, 7, 14, 28, 31, 62, 124, 217, 434, 868]]
[869, [1, 11, 79, 869]]
[870, [1, 2, 3, 5, 6, 10, 15, 29, 30, 58, 87, 145, 174, 290,
435, 870]]
[871, [1, 13, 67, 871]]
[872, [1, 2, 4, 8, 109, 218, 436, 872]]
[873, [1, 3, 9, 97, 291, 873]]
[874, [1, 2, 19, 23, 38, 46, 437, 874]]
[875, [1, 5, 7, 25, 35, 125, 175, 875]]
[876, [1, 2, 3, 4, 6, 12, 73, 146, 219, 292, 438, 876]]
[877, [1, 877]]
[878, [1, 2, 439, 878]]
[879, [1, 3, 293, 879]]
[880, [1, 2, 4, 5, 8, 10, 11, 16, 20, 22, 40, 44, 55, 80,
88, 110, 176, 220, 440, 880]]
[881, [1, 881]]
[882, [1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 49, 63, 98, 126,
147, 294, 441, 882]]
[883, [1, 883]]
[884, [1, 2, 4, 13, 17, 26, 34, 52, 68, 221, 442, 884]]
[885, [1, 3, 5, 15, 59, 177, 295, 885]]
[886, [1, 2, 443, 886]]
[887, [1, 887]]
[888, [1, 2, 3, 4, 6, 8, 12, 24, 37, 74, 111, 148, 222, 296,
444, 888]]
[889, [1, 7, 127, 889]]
[890, [1, 2, 5, 10, 89, 178, 445, 890]]
[891, [1, 3, 9, 11, 27, 33, 81, 99, 297, 891]]
[892, [1, 2, 4, 223, 446, 892]]
[893, [1, 19, 47, 893]]
[894, [1, 2, 3, 6, 149, 298, 447, 894]]
[895, [1, 5, 179, 895]]
[896, [1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 64, 112, 128, 224,
448, 896]]
[897, [1, 3, 13, 23, 39, 69, 299, 897]]
[898, [1, 2, 449, 898]]
[899, [1, 29, 31, 899]]
[900, [1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36,
45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450, 900]]
[901, [1, 17, 53, 901]]
[902, [1, 2, 11, 22, 41, 82, 451, 902]]
[903, [1, 3, 7, 21, 43, 129, 301, 903]]
[904, [1, 2, 4, 8, 113, 226, 452, 904]]
[905, [1, 5, 181, 905]]
[906, [1, 2, 3, 6, 151, 302, 453, 906]]
[907, [1, 907]]
[908, [1, 2, 4, 227, 454, 908]]
[909, [1, 3, 9, 101, 303, 909]]
[910, [1, 2, 5, 7, 10, 13, 14, 26, 35, 65, 70, 91, 130, 182,
455, 910]]
[911, [1, 911]]
[912, [1, 2, 3, 4, 6, 8, 12, 16, 19, 24, 38, 48, 57, 76,
114, 152, 228, 304, 456, 912]]
[913, [1, 11, 83, 913]]
[914, [1, 2, 457, 914]]
[[915, [1, 3, 5, 15, 61, 183, 305,
915]]
[916, [1, 2, 4, 229, 458, 916]]
[917, [1, 7, 131, 917]]
[918, [1, 2, 3, 6, 9, 17, 18, 27,
34, 51, 54, 102, 153, 306, 459, 918]]
[919, [1, 919]]
[920, [1, 2, 4, 5, 8, 10, 20, 23,
40, 46, 92, 115, 184, 230, 460, 920]]
[921, [1, 3, 307, 921]]
[922, [1, 2, 461, 922]]
[923, [1, 13, 71, 923]]
[924, [1, 2, 3, 4, 6, 7, 11, 12,
14, 21, 22, 28, 33, 42, 44, 66, 77, 84, 132, 154, 231, 308, 462, 924]]
[925, [1, 5, 25, 37, 185, 925]]
[926, [1, 2, 463, 926]]
[927, [1, 3, 9, 103, 309, 927]]
[928, [1, 2, 4, 8, 16, 29, 32, 58,
116, 232, 464, 928]]
[929, [1, 929]]
[930, [1, 2, 3, 5, 6, 10, 15, 30,
31, 62, 93, 155, 186, 310, 465, 930]]
[931, [1, 7, 19, 49, 133, 931]]
[932, [1, 2, 4, 233, 466, 932]]
[933, [1, 3, 311, 933]]
[934, [1, 2, 467, 934]]
[935, [1, 5, 11, 17, 55, 85, 187,
935]]
[936, [1, 2, 3, 4, 6, 8, 9, 12,
13, 18, 24, 26, 36, 39, 52, 72, 78, 104, 117, 156, 234, 312, 468, 936]]
[937, [1, 937]]
[938, [1, 2, 7, 14, 67, 134, 469,
938]]
[939, [1, 3, 313, 939]]
[940, [1, 2, 4, 5, 10, 20, 47, 94,
188, 235, 470, 940]]
[941, [1, 941]]
[942, [1, 2, 3, 6, 157, 314, 471,
942]]
[943, [1, 23, 41, 943]]
[944, [1, 2, 4, 8, 16, 59, 118,
236, 472, 944]]
[945, [1, 3, 5, 7, 9, 15, 21, 27,
35, 45, 63, 105, 135, 189, 315, 945]]
[946, [1, 2, 11, 22, 43, 86, 473,
946]]
[947, [1, 947]]
[948, [1, 2, 3, 4, 6, 12, 79, 158,
237, 316, 474, 948]]
[949, [1, 13, 73, 949]]
[950, [1, 2, 5, 10, 19, 25, 38,
50, 95, 190, 475, 950]]
[951, [1, 3, 317, 951]]
[952, [1, 2, 4, 7, 8, 14, 17, 28,
34, 56, 68, 119, 136, 238, 476, 952]]
[953, [1, 953]]
[954, [1, 2, 3, 6, 9, 18, 53, 106,
159, 318, 477, 954]]
[955, [1, 5, 191, 955]]
[956, [1, 2, 4, 239, 478, 956]]
[957, [1, 3, 11, 29, 33, 87, 319,
957]]
[958, [1, 2, 479, 958]]
[959, [1, 7, 137, 959]]
[960, [1, 2, 3, 4, 5, 6, 8, 10,
12, 15, 16, 20, 24, 30, 32, 40, 48, 60, 64, 80, 96, 120, 160, 192, 240, 320,
480, 960]]
[961, [1, 31, 961]]
[962, [1, 2, 13, 26, 37, 74, 481,
962]]
[963, [1, 3, 9, 107, 321, 963]]
[964, [1, 2, 4, 241, 482, 964]]
[965, [1, 5, 193, 965]]
[966, [1, 2, 3, 6, 7, 14, 21, 23,
42, 46, 69, 138, 161, 322, 483, 966]]
[967, [1, 967]]
[968, [1, 2, 4, 8, 11, 22, 44, 88,
121, 242, 484, 968]]
[969, [1, 3, 17, 19, 51, 57, 323,
969]]
[970, [1, 2, 5, 10, 97, 194, 485,
970]]
[971, [1, 971]]
[972, [1, 2, 3, 4, 6, 9, 12, 18,
27, 36, 54, 81, 108, 162, 243, 324, 486, 972]]
[973, [1, 7, 139, 973]]
[974, [1, 2, 487, 974]]
[975, [1, 3, 5, 13, 15, 25, 39,
65, 75, 195, 325, 975]]
[976, [1, 2, 4, 8, 16, 61, 122,
244, 488, 976]]
[977, [1, 977]]
[978, [1, 2, 3, 6, 163, 326, 489,
978]]
[979, [1, 11, 89, 979]]
[980, [1, 2, 4, 5, 7, 10, 14, 20,
28, 35, 49, 70, 98, 140, 196, 245, 490, 980]]
[981, [1, 3, 9, 109, 327, 981]]
[982, [1, 2, 491, 982]]
[983, [1, 983]]
[984, [1, 2, 3, 4, 6, 8, 12, 24,
41, 82, 123, 164, 246, 328, 492, 984]]
[985, [1, 5, 197, 985]]
[986, [1, 2, 17, 29, 34, 58, 493,
986]]
[987, [1, 3, 7, 21, 47, 141, 329,
987]]
[988, [1, 2, 4, 13, 19, 26, 38,
52, 76, 247, 494, 988]]
[989, [1, 23, 43, 989]]
[990, [1, 2, 3, 5, 6, 9, 10, 11,
15, 18, 22, 30, 33, 45, 55, 66, 90, 99, 110, 165, 198, 330, 495, 990]]
[991, [1, 991]]
[992, [1, 2, 4, 8, 16, 31, 32, 62,
124, 248, 496, 992]]
[993, [1, 3, 331, 993]]
[994, [1, 2, 7, 14, 71, 142, 497,
994]]
[995, [1, 5, 199, 995]]
[996, [1, 2, 3, 4, 6, 12, 83, 166, 249, 332, 498, 996]]
[997, [1, 997]]
[998, [1, 2, 499, 998]]
[999, [1, 3, 9, 27, 37, 111, 333,
999]]
[1000, [1, 2, 4, 5, 8, 10, 20, 25,
40, 50, 100, 125, 200, 250, 500, 1000]]]
Теперь
несложно посчитать и сумму делителей чисел от 1 до 1000(которые тоже были
получены с помощью программы Derive (по формуле 2.), теперь делители «a» просто
складывались):
[1, 1]
[2, 3]
[3, 4]
[4, 7]
[5, 6]
[6, 12]
[7, 8]
[8, 15]
[9, 13]
[10, 18]
[11, 12]
[12, 28]
[13, 14]
[14, 24]
[15, 24]
[16, 31]
[17, 18]
[18, 39]
[19, 20]
[20, 42]
[21, 32]
[22, 36]
[23, 24]
[24, 60]
[25, 31]
[26, 42]
[27, 40]
[28, 56]
[29, 30]
[30, 72]
[31, 32]
[32, 63]
[33, 48]
[34, 54]
[35, 48]
[36, 91]
[37, 38]
[38, 60]
[39, 56]
[40, 90]
[41, 42]
[42, 96]
[43, 44]
[44, 84]
[45, 78]
[46, 72]
[47, 48]
[48, 124]
[50, 93]
[51, 72]
[52, 98]
[53, 54]
[54, 120]
[55, 72]
[56, 120]
[57, 80]
[58, 90]
[59, 60]
[60, 168]
[61, 62]
[62, 96]
[63, 104]
[64, 127]
[65, 84]
[66, 144]
[67, 68]
[68, 126]
[69, 96]
[70, 144]
[71, 72]
[72, 195]
[73, 74]
[74, 114]
[75, 124]
[76, 140]
[77, 96]
[78, 168]
[79, 80]
[80, 186]
[81, 121]
[82, 126]
[83, 84]
[84, 224]
[85, 108]
[86, 132]
[87, 120]
[88, 180]
[89, 90]
[90, 234]
[91, 112]
[92, 168]
[93, 128]
[94, 144]
[95, 120]
[96, 252]
[97, 98]
[98, 171]
[99, 156]
[100, 217]
[101, 102]
[102, 216]
[103, 104]
[104, 210]
[105, 192]
[106, 162]
[107, 108]
[108, 280]
[109, 110]
[110, 216]
[111, 152]
[112, 248]
[113, 114]
[114, 240]
[115, 144]
[116, 210]
[117, 182]
[118, 180]
[119, 144]
[120, 360]
[121, 133]
[122, 186]
[123, 168]
[124, 224]
[125, 156]
[126, 312]
[127, 128]
[128, 255]
[129, 176]
[130, 252]
[131, 132]
[132, 336]
[133, 160]
[134, 204]
[135, 240]
[136, 270]
[137, 138]
[138, 288]
[139, 140]
[140, 336]
[141, 192]
[142, 216]
[143, 168]
[144, 403]
[145, 180]
[146, 222]
[147, 228]
[148, 266]
[149, 150]
[150, 372]
[151, 152]
[152, 300]
[153, 234]
[154, 288]
[155, 192]
[156, 392]
[157, 158]
[158, 240]
[159, 216]
[160, 378]
[161, 192]
[162, 363]
[163, 164]
[164, 294]
[165, 288]
[166, 252]
[167, 168]
[168, 480]
[169, 183]
[170, 324]
[171, 260]
[172, 308]
[173, 174]
[174, 360]
[175, 248]
[176, 372]
[177, 240]
[178, 270]
[179, 180]
[180, 546]
[181, 182]
[182, 336]
[183, 248]
[184, 360]
[185, 228]
[186, 384]
[187, 216]
[188, 336]
[189, 320]
[190, 360]
[191, 192]
[192, 508]
[193, 194]
[194, 294]
[195, 336]
[196, 399]
[197, 198]
[198, 468]
[199, 200]
[200, 465]
[201, 272]
[202, 306]
[203, 240]
[204, 504]
[205, 252]
[206, 312]
[207, 312]
[208, 434]
[209, 240]
[210, 576]
[211, 212]
[212, 378]
[213, 288]
[214, 324]
[215, 264]
[216, 600]
[217, 256]
[218, 330]
[219, 296]
[220, 504]
[221, 252]
[222, 456]
[223, 224]
[224, 504]
[225, 403]
[226, 342]
[227, 228]
[228, 560]
[229, 230]
[230, 432]
[231, 384]
[232, 450]
[233, 234]
[234, 546]
[235, 288]
[236, 420]
[237, 320]
[238, 432]
[239, 240]
[240, 744]
[241, 242]
[242, 399]
[243, 364]
[244, 434]
[245, 342]
[246, 504]
[247, 280]
[248, 480]
[249, 336]
[250, 468]
[251, 252]
[252, 728]
[253, 288]
[254, 384]
[255, 432]
[256, 511]
[257, 258]
[258, 528]
[259, 304]
[260, 588]
[261, 390]
[262, 396]
[263, 264]
[264, 720]
[265, 324]
[266, 480]
[267, 360]
[268, 476]
[269, 270]
[270, 720]
[271, 272]
[272, 558]
[273, 448]
[274, 414]
[275, 372]
[276, 672]
[277, 278]
[278, 420]
[279, 416]
[280, 720]
[281, 282]
[282, 576]
[283, 284]
[284, 504]
[285, 480]
[286, 504]
[287, 336]
[288, 819]
[289, 307]
[290, 540]
[291, 392]
[292, 518]
[293, 294]
[294, 684]
[295, 360]
[296, 570]
[297, 480]
[298, 450]
[299, 336]
[300, 868]
[301, 352]
[302, 456]
[303, 408]
[304, 620]
[305, 372]
[306, 702]
[307, 308]
[308, 672]
[309, 416]
[310, 576]
[311, 312]
[312, 840]
[313, 314]
[314, 474]
[315, 624]
[316, 560]
[317, 318]
[318, 648]
[319, 360]
[320, 762]
[321, 432]
[322, 576]
[323, 360]
[324, 847]
[325, 434]
[326, 492]
[327, 440]
[328, 630]
[329, 384]
[330, 864]
[331, 332]
[332, 588]
[333, 494]
[334, 504]
[335, 408]
[336, 992]
[337, 338]
[338, 549]
[339, 456]
[340, 756]
[341, 384]
[342, 780]
[343, 400]
[344, 660]
[345, 576]
[346, 522]
[347, 348]
[348, 840]
[349, 350]
[350, 744]
[351, 560]
[352, 756]
[353, 354]
[354, 720]
[355, 432]
[356, 630]
[357, 576]
[358, 540]
[359, 360]
[360, 1170]
[361, 381]
[362, 546]
[363, 532]
[364, 784]
[365, 444]
[366, 744]
[367, 368]
[368, 744]
[369, 546]
[370, 684]
[371, 432]
[372, 896]
[373, 374]
[374, 648]
[375, 624]
[376, 720]
[377, 420]
[378, 960]
[379, 380]
[380, 840]
[381, 512]
[382, 576]
[383, 384]
[384, 1020]
[385, 576]
[386, 582]
[387, 572]
[388, 686]
[389, 390]
[390, 1008]
[391, 432]
[392, 855]
[393, 528]
[394, 594]
[395, 480]
[396, 1092]
[397, 398]
[398, 600]
[399, 640]
[401, 402]
[402, 816]
[403, 448]
[404, 714]
[405, 726]
[406, 720]
[407, 456]
[408, 1080]
[409, 410]
[410, 756]
[411, 552]
[412, 728]
[413, 480]
[414, 936]
[415, 504]
[416, 882]
[417, 560]
[418, 720]
[419, 420]
[420, 1344]
[421, 422]
[422, 636]
[423, 624]
[424, 810]
[425, 558]
[426, 864]
[427, 496]
[428, 756]
[429, 672]
[430, 792]
[431, 432]
[432, 1240]
[433, 434]
[434, 768]
[435, 720]
[436, 770]
[437, 480]
[438, 888]
[439, 440]
[440, 1080]
[441, 741]
[442, 756]
[443, 444]
[444, 1064]
[445, 540]
[446, 672]
[447, 600]
[448, 1016]
[449, 450]
[450, 1209]
[451, 504]
[452, 798]
[453, 608]
[454, 684]
[455, 672]
[456, 1200]
[457, 458]
[458, 690]
[459, 720]
[460, 1008]
[461, 462]
[462, 1152]
[463, 464]
[464, 930]
[465, 768]
[466, 702]
[467, 468]
[468, 1274]
[469, 544]
[470, 864]
[471, 632]
[472, 900]
[473, 528]
[474, 960]
[475, 620]
[476, 1008]
[477, 702]
[478, 720]
[479, 480]
[480, 1512]
[481, 532]
[482, 726]
[483, 768]
[484, 931]
[485, 588]
[486, 1092]
[487, 488]
[488, 930]
[489, 656]
[490, 1026]
[491, 492]
[492, 1176]
[493, 540]
[494, 840]
[495, 936]
[496, 992]
[497, 576]
[498, 1008]
[499, 500]
[500, 1092]
[501, 672]
[502, 756]
[503, 504]
[504, 1560]
[505, 612]
[506, 864]
[507, 732]
[508, 896]
[509, 510]
[510, 1296]
[511, 592]
[512, 1023]
[513, 800]
[514, 774]
[515, 624]
[516, 1232]
[517, 576]
[518, 912]
[519, 696]
[520, 1260]
[521, 522]
[522, 1170]
[523, 524]
[524, 924]
[525, 992]
[526, 792]
[527, 576]
[528, 1488]
[529, 553]
[530, 972]
[531, 780]
[532, 1120]
[533, 588]
[534, 1080]
[535, 648]
[536, 1020]
[537, 720]
[538, 810]
[539, 684]
[540, 1680]
[541, 542]
[542, 816]
[543, 728]
[544, 1134]
[545, 660]
[546, 1344]
[547, 548]
[548, 966]
[549, 806]
[550, 1116]
[551, 600]
[552, 1440]
[553, 640]
[554, 834]
[555, 912]
[556, 980]
[557, 558]
[558, 1248]
[559, 616]
[560, 1488]
[561, 864]
[562, 846]
[563, 564]
[564, 1344]
[565, 684]
[566, 852]
[567, 968]
[568, 1080]
[569, 570]
[570, 1440]
[571, 572]
[572, 1176]
[573, 768]
[574, 1008]
[575, 744]
[576, 1651]
[577, 578]
[578, 921]
[579, 776]
[580, 1260]
[581, 672]
[582, 1176]
[583, 648]
[584, 1110]
[585, 1092]
[586, 882]
[587, 588]
[588, 1596]
[589, 640]
[590, 1080]
[591, 792]
[592, 1178]
[593, 594]
[594, 1440]
[595, 864]
[596, 1050]
[597, 800]
[598, 1008]
[599, 600]
[600, 1860]
[601, 602]
[602, 1056]
[603, 884]
[604, 1064]
[605, 798]
[606, 1224]
[607, 608]
[608, 1260]
[609, 960]
[610, 1116]
[611, 672]
[612, 1638]
[613, 614]
[614, 924]
[615, 1008]
[616, 1440]
[617, 618]
[618, 1248]
[619, 620]
[620, 1344]
[621, 960]
[622, 936]
[623, 720]
[624, 1736]
[625, 781]
[626, 942]
[627, 960]
[628, 1106]
[629, 684]
[630, 1872]
[631, 632]
[632, 1200]
[633, 848]
[634, 954]
[635, 768]
[636, 1512]
[637, 798]
[638, 1080]
[639, 936]
[640, 1530]
[641, 642]
[642, 1296]
[643, 644]
[644, 1344]
[645, 1056]
[646, 1080]
[647, 648]
[648, 1815]
[649, 720]
[650, 1302]
[651, 1024]
[652, 1148]
[653, 654]
[654, 1320]
[655, 792]
[656, 1302]
[657, 962]
[658, 1152]
[659, 660]
[660, 2016]
[661, 662]
[662, 996]
[663, 1008]
[664, 1260]
[665, 960]
[666, 1482]
[667, 720]
[668, 1176]
[669, 896]
[670, 1224]
[671, 744]
[672, 2016]
[673, 674]
[674, 1014]
[675, 1240]
[676, 1281]
[677, 678]
[678, 1368]
[679, 784]
[680, 1620]
[681, 912]
[682, 1152]
[683, 684]
[684, 1820]
[685, 828]
[686, 1200]
[687, 920]
[688, 1364]
[689, 756]
[690, 1728]
[691, 692]
[692, 1218]
[693, 1248]
[694, 1044]
[695, 840]
[696, 1800]
[697, 756]
[698, 1050]
[699, 936]
[700, 1736]
[701, 702]
[702, 1680]
[703, 760]
[704, 1524]
[705, 1152]
[706, 1062]
[707, 816]
[708, 1680]
[709, 710]
[710, 1296]
[711, 1040]
[712, 1350]
[713, 768]
[714, 1728]
[715, 1008]
[716, 1260]
[717, 960]
[718, 1080]
[719, 720]
[720, 2418]
[721, 832]
[722, 1143]
[723, 968]
[724, 1274]
[725, 930]
[726, 1596]
[727, 728]
[728, 1680]
[729, 1093]
[730, 1332]
[731, 792]
[732, 1736]
[733, 734]
[734, 1104]
[735, 1368]
[736, 1512]
[737, 816]
[738, 1638]
[739, 740]
[740, 1596]
[741, 1120]
[742, 1296]
[743, 744]
[744, 1920]
[745, 900]
[746, 1122]
[747, 1092]
[748, 1512]
[749, 864]
[750, 1872]
[752, 1488]
[753, 1008]
[754, 1260]
[755, 912]
[756, 2240]
[757, 758]
[758, 1140]
[759, 1152]
[760, 1800]
[761, 762]
[762, 1536]
[763, 880]
[764, 1344]
[765, 1404]
[766, 1152]
[767, 840]
[768, 2044]
[769, 770]
[770, 1728]
[771, 1032]
[772, 1358]
[773, 774]
[774, 1716]
[775, 992]
[776, 1470]
[777, 1216]
[778, 1170]
[779, 840]
[780, 2352]
[781, 864]
[782, 1296]
[783, 1200]
[784, 1767]
[785, 948]
[786, 1584]
[787, 788]
[788, 1386]
[789, 1056]
[790, 1440]
[791, 912]
[792, 2340]
[793, 868]
[794, 1194]
[795, 1296]
[796, 1400]
[797, 798]
[798, 1920]
[799, 864]
[800, 1953]
[801, 1170]
[802, 1206]
[803, 888]
[804, 1904]
[805, 1152]
[806, 1344]
[807, 1080]
[808, 1530]
[809, 810]
[810, 2178]
[811, 812]
[812, 1680]
[813, 1088]
[814, 1368]
[815, 984]
[816, 2232]
[817, 880]
[818, 1230]
[819, 1456]
[820, 1764]
[821, 822]
[822, 1656]
[823, 824]
[824, 1560]
[825, 1488]
[826, 1440]
[827, 828]
[828, 2184]
[829, 830]
[830, 1512]
[831, 1112]
[832, 1778]
[833, 1026]
[834, 1680]
[835, 1008]
[836, 1680]
[837, 1280]
[838, 1260]
[839, 840]
[840, 2880]
[841, 871]
[842, 1266]
[843, 1128]
[844, 1484]
[845, 1098]
[846, 1872]
[847, 1064]
[848, 1674]
[849, 1136]
[850, 1674]
[851, 912]
[852, 2016]
[853, 854]
[854, 1488]
[855, 1560]
[856, 1620]
[857, 858]
[858, 2016]
[859, 860]
[860, 1848]
[861, 1344]
[862, 1296]
[863, 864]
[864, 2520]
[865, 1044]
[866, 1302]
[867, 1228]
[868, 1792]
[869, 960]
[870, 2160]
[871, 952]
[872, 1650]
[873, 1274]
[874, 1440]
[875, 1248]
[876, 2072]
[877, 878]
[878, 1320]
[879, 1176]
[880, 2232]
[881, 882]
[882, 2223]
[883, 884]
[884, 1764]
[885, 1440]
[886, 1332]
[887, 888]
[888, 2280]
[889, 1024]
[890, 1620]
[891, 1452]
[892, 1568]
[893, 960]
[894, 1800]
[895, 1080]
[896, 2040]
[897, 1344]
[898, 1350]
[899, 960]
[900, 2821]
[901, 972]
[902, 1512]
[903, 1408]
[904, 1710]
[905, 1092]
[906, 1824]
[907, 908]
[908, 1596]
[909, 1326]
[910, 2016]
[911, 912]
[912, 2480]
[913, 1008]
[914, 1374]
[915, 1488]
[916, 1610]
[917, 1056]
[918, 2160]
[919, 920]
[920, 2160]
[921, 1232]
[922, 1386]
[923, 1008]
[924, 2688]
[925, 1178]
[926, 1392]
[927, 1352]
[928, 1890]
[929, 930]
[930, 2304]
[931, 1140]
[932, 1638]
[933, 1248]
[934, 1404]
[935, 1296]
[936, 2730]
[937, 938]
[938, 1632]
[939, 1256]
[940, 2016]
[941, 942]
[942, 1896]
[943, 1008]
[944, 1860]
[945, 1920]
[946, 1584]
[947, 948]
[948, 2240]
[949, 1036]
[950, 1860]
[951, 1272]
[952, 2160]
[953, 954]
[954, 2106]
[955, 1152]
[956, 1680]
[957, 1440]
[958, 1440]
[959, 1104]
[960, 3048]
[961, 993]
[962, 1596]
[963, 1404]
[964, 1694]
[965, 1164]
[966, 2304]
[967, 968]
[968, 1995]
[969, 1440]
[970, 1764]
[971, 972]
[972, 2548]
[973, 1120]
[974, 1464]
[975, 1736]
[976, 1922]
[977, 978]
[978, 1968]
[979, 1080]
[980, 2394]
[981, 1430]
[982, 1476]
[983, 984]
[984, 2520]
[985, 1188]
[986, 1620]
[987, 1536]
[988, 1960]
[989, 1056]
[990, 2808]
[991, 992]
[992, 2016]
[993, 1328]
[994, 1728]
[995, 1200]
[996, 2352]
[997, 998]
[998, 1500]
[999, 1520]
[1000, 2340]
Теперь
посмотрим, все ли числа являются суммой делителей какого-либо числа и есть ли
такие числа сумма делителей которых равна (в первых двух сотнях).
Ниже
приведена таблица: [[4, 7]](на втором месте сумма делителей, а на первом число
с данной суммой делителей) … [[1, 1]], [2] (т.е. нет такого числа с суммой
делителей равной двум):
[1,1]
[2]
[2,3]
[3,4]
[5]
[5,6]
[4,7]
[7,8]
[9]
[10]
[11]
[6,12]
[11, 12]
[9,13]
[13,14]
[8,15]
[16]
[17]
[10,18]
[17,18]
[19]
[19.20]
[21]
[22]
[23]
[14,24]
[15,24]
[23,24]
[25]
[26]
[27]
[12, 28].
[29]
[29,30]
[16,31]
[25.31]
[21,32]
[31,32]
[33]
[34]
[35]
[22,36]
[37]
[37,38]
[18,39]
[27, 40]
[41]
[20,42]
[26,42]
[41,42].
[43]
[43,44].
[45]
[46]
[47]
[33,48].
[35,4 8]
[47,48]
[49]
[50]
[51]
[52]
[53]
[34,54]
[53, 54]
[55]
[28,56]
[39.56]
[49,57]
[58]
[59]
[24,60]
[38.60]
[59,60]
[61]
[61,62]
[32,63]
[64]
[65]
[66]
[67]
[67, 68]
[69]
[70]
[71]
[30,72]
[46,72]
[51,72]
[55,72]
[71,72]
[73]
[73,74]
[75]
[76]
[77]
[45,78]
[79]
[57,80]
[79,80]
[82]
[83]
[44,84]
[65,84]
[83,84]
[85]
[86]
[87]
[88]
[89]
[40, 90]
[58,90]
[89,90]
[36,91]
[92]
[50,93].
[94]
[95]
[42, 96]
[62,96]
[69,96]
[77,96]
[97]
[52,98]
[97,98]
[99]
[100]
[101]
[102]
[103]
[63,104]
[105]
[106]
[107]
[85,108]
[109]
[110]
[111]
[91, 112]
[113]
[74,114],
[115]
[116]
[117]
[118]
[119]
[54,120]
[56,120]
[87,120]
[95,120]
[81,121]
[122]
[123]
[48,124]
[75, 124]
[125]
[68,126]
[82.126]
[64,127]
[9 3,128]
[129]
[130]
[131]
[86,132]
[133]
[134]
[135]
[136]
[137]
[138]
[139]
[76,140]
[141]
[142]
[143]
[66,144]
[70,144]
[94,144]
[145]
[146]
[147]
[178]
[149]
[150]
[151]
[152]
[153]
[154]
[155]
[99,156]
[157]
[158]
[159]
[160]
[161]
[162]
[163]
[164]
[165]
[166]
[167]
[60,168]
[78,168]
[92,168]
[169]
[170]
[98,171]
[172]
[173]
[174]
[175]
[176]
[177]
[178]
[179]
[88,180]
[181]
[182]
[183]
[184]
[185]
[80,186]
[187]
[188]
[189]
[190]
[191]
[192]
[193]
[194]
[72,195]
[196]
[197]
[198]
[199]
[200]
Как
мы заметили, есть такие числа, которые не являются суммой делителей ни одного
числа и так же есть такие числа, которые являются суммой делителей ни одного, а
нескольких чисел. Теперь посмотрим только те числа, которые являются суммой
делителей ни одного, а нескольких чисел:
[6,12], [11,12]
[10,18], [17,18]
[14,24], [15,24],
[23,24]
[16,31]. [25,31]
[21,32], [31,32]
[20, 42], [26,42],
[41,42]
[33,48], [35,48],
[47,48]
[34,5 4], [53,54]
[28,56], [39,56]
[24,60], [38,60], [59,
60]
[30,72], [46,72],
[51,72], [55,72], [71,72]
[57,80], [79,80]
[44,84], [65,84],
[83,84]
[40,90], [58, 9 0],
[89,90]
[42,96], [62,96],
[69,96], [77,96]
[52,98], [97,98]
[54,120], [56, 120],
[87,120], [95,120]
[48,124], [75,124]
[68,126], [82,126]
[66,144], [70, 144],
[94,144]
[60,168], [78,168],
[92,168]
Отсюда можно сделать вывод, что нахождение числа по его сумме делителей не
всегда возможно и не всегда однозначно.
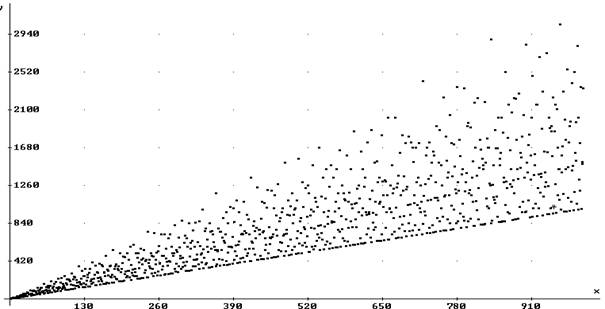 |
Теперь построим график. По оси Х расположим
числа, а по оси Y их сумму делителей (числа от 1 до 1000):
Посмотрим,
что же у нас получилось: на графике отчётливо просматриваются несколько прямых
линий, например, нижняя это – простые числа. Верхняя граница – это наиболее
сложные числа (имеющие наибольшее количество делителей) — это не прямая, но и
не парабола. Скорее всего, – это показательная функция (у = ах).
В мемуарах
Эйлера я нашел много интересных мне рассуждений(σ(n) –
сумма делителей числа n): Определив значение σ(n) мы ясно видим, что если p –
простое, то σ(p)= p
+ 1. σ(1)=1, а
если число n – составное, то σ(n)>1 + n.
Если a, b, c, d – различные простые числа, то мы видим:
σ(ab)=1+a+b+ab=(1+a)(1+b)= σ(a)σ(b)
σ(abcd)=
σ(a)σ(b)σ(c)σ(d)
σ(a^2)=1+a+a2=
σ(a^3)=1+a+a2+a3=
И вообще
σ(nn)=
Пользуясь
этим:
σ(aqbwcedr)= σ(aq)σ(bw)σ(ce)σ(dr)
Например
σ(360), 360 = 23*32*5 => σ(23)
σ(32) σ(5)=15*13*6=1170.
Чтобы показать последовательность сумм делителей приведём таблицу:
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
— |
1 |
3 |
4 |
7 |
6 |
12 |
8 |
15 |
13 |
|
10 |
18 |
12 |
28 |
14 |
24 |
24 |
31 |
18 |
39 |
20 |
|
20 |
42 |
32 |
36 |
24 |
60 |
31 |
42 |
40 |
56 |
30 |
|
30 |
72 |
32 |
63 |
48 |
54 |
48 |
91 |
38 |
60 |
56 |
|
40 |
90 |
42 |
96 |
44 |
84 |
78 |
72 |
48 |
124 |
57 |
|
50 |
93 |
72 |
98 |
54 |
120 |
72 |
120 |
80 |
90 |
60 |
|
60 |
168 |
62 |
96 |
104 |
127 |
84 |
144 |
68 |
126 |
96 |
|
70 |
144 |
72 |
195 |
74 |
114 |
424 |
140 |
96 |
168 |
80 |
|
80 |
186 |
121 |
126 |
84 |
224 |
108 |
132 |
120 |
180 |
90 |
|
90 |
234 |
112 |
168 |
128 |
144 |
120 |
252 |
98 |
171 |
156 |
Если
σ(n) обозначает член любой этой последовательности, а σ(n — 1),
σ(n — 2), σ(n — 3)… предшествующие члены, то σ(n) всегда можно
получить по нескольким предыдущим членам:
σ(n) = σ(n — 1) + σ(n — 2) — σ(n — 5) — σ(n — 7) +
σ(n — 12) + σ(n — 15) — σ(n — 22) — σ(n – 26) + … (**)
Знаки «+» «-» в правой части формулы попарно чередуются. Закон чисел 1, 2, 5,
7, 12, 15…,которые мы должны вычитать из рассматриваемого числа n,
станет ясен если мы возьмем их разности:
Числа:1, 2, 5, 7, 12, 15, 22,
26, 35, 40, 51, 57, 70, 77, 92, 100…
Разности: 1, 3, 2, 5, 3,
7, 4, 9, 5, 11, 6, 13, 7, 15, 8…
В самом
деле, мы имеем здесь поочередно все целые числа 1, 2, 3, 4, 5, 6, 7… и нечетные
3, 5, 7,9 11…
Хотя эта последовательность бесконечна, мы должны в каждом случае брать только
те члены, для которых числа стоящие под знаком σ, еще положительны, и
опускать σ для отрицательных чисел. Если в нашей формуле встретиться
σ(0), то, поскольку его значение само по себе является неопределённым, мы
должны подставить вместо σ(0) рассматриваемое число n. Примеры:
σ(1)
= σ(0)
=1 = 1
σ(2)
= σ(1) + σ(0) = 1 +
2 = 3
…
σ(20)
=
σ(19)+σ(18)-σ(15)-σ(13)+9σ(8)+σ(5)=20+39-24-14+15+6=
42
Доказательство теоремы (**) я приводить не буду.
Вообще, найти сумму всех делителей числа можно с
помощью канонического разложения натурального числа (это уже было сказано
выше). Сумму делителей числа n обозначают σ(n). Легко найти σ(n) для
небольших натуральных чисел, например σ(12) = 1+2+3+4+6+12=28(это было
приведено выше). Но при достаточно больших числах отыскивание всех делителей, а
тем более их суммы становится затруднительным. Совсем другое дело, если уже
известно, что каноническое
разложение
числа n таково:.
Его
делителями являются все числа , для которых 0
≤ βs ≤ αs, s = 1, …, k.
Ясно, что σ(n) представляет собой сумму всех таких чисел при различных
значениях показателей
β1,
β2, … βk. Этот результат мы получим раскрыв
скобки в произведении
По
формуле конечного числа членов геометрической прогрессии приходим к равенству
(*)
По
этой формуле σ(360) = .
Формулу
для вычисления значения функции σ(n) вывел замечательный английский
математик Джон Валлис(1616 — 1703) – один из основателей и первых членов
Лондонского Королевства общества (Академии наук). Он был первым из английских
математиков, начавших заниматься математическим анализом. Ему принадлежат
многие обозначения и термины, применяемые сейчас в математике, в частности знак
∞ для обозначения бесконечности. Валлис вывел удивительную формулу,
представляющую число π в виде бесконечного произведения:
Д.
Валлис много занимался комбинаторикой и её приложениями к теории шифров, не без
основания считая себя родоначальником новой науки – криптологии (от греч.
«криптос» — тайный, «логос» — наука, учение). Он был одним из лучших
шифровальщиков своего времени и по поручению министра полиции Терло занимался в
республиканском правительстве Кромвеля расшифровкой посланий монархических
заговорщиков.
С функцией σ(n) связан ряд любопытных задач. Например:
1.) Найти пару целых чисел, удовлетворяющих условию: σ(m1)=m2, σ(m2)=m1.
Некоторые
из них не удаётся решить даже с использованием формулы (*). Так, например, не
иначе как подбором можно найти числа, для которых σ(n) есть квадрат
некоторого натурального числа. Такими числами являются 22, 66, 70, 81, 343,
1501, 4479865. Вот ещё две задачи, приведённые в 1657 г. Пьером Ферма:
1.)
найти такое m, для которого
σ(m3) – квадрат натурального числа (Ферма нашёл не одно решение
этой задачи);
2.)
найти такое m, для которого
σ(m2) – куб натурального числа.
Например, одним из решений первой задачи является m =
7, а для второй m = 43098.
С помощью программы Derive, я
попробовал найти ещё решения и у меня этого не получилось. (я рассматривал
σ(m3) = n2,
где m принимает
значения от 1 до 1000, а n от 1
до 5000 в 1.) и тоже самое в 2.) )
Формулы:
1. DELITELI(m) :=
SELECT(MOD(m, n) = 0, n, 1, m)
DIMENSION(DELITELI(m))
2. SUMMADELITELEY(m)
:= Σ ELEMENT(DELITELI(m), i)
i=1




