Как найти сумму целых точек - AvtoShod.ru - решение различных проблем

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Источник

Главная › ЕГЭ. Производная и первообразная

Найти сумму целых точек на промежутке возрастания по графику производной

Автор: Ирина Гайкова

Комментариев нет

742

На рисунке изображен график y = f/(x)— производной функции f(x), определенной на интервале(-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Интересная статья? Поделитесь ею пожалуйста с другими:

Facebook

Хотите обучаться математике индивидуально?
Запишитесь на консультацию.

Мы храним ваши данные в тайне

Похожие записи:

Определите количество целых точек, в которых производная функции f(x) отрицательна
Найдите количество точек минимума функции, принадлежащих отрезку [−13;1]
На рисунке изображен график производной функции f(x), определенной на интервале (- 10: 2)

Оставьте свой комментарий:

на Блоге
в Вконтакте
в Фейсбук

:-D =-O *CRAZY* Еще смайлы

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий

Имя *

Email *

Вебсайт

Получать новые комментарии по электронной почте. Вы можете подписаться без комментирования.

Нажимая на кнопку «Отправить комментарий», я соглашаюсь с политикой обработки персональных данных

Источник

Всего: 15 1–15

Добавить в вариант

На рисунке изображен график функции f(x), определенной на интервале (−7; 4). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график функции y  =  f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Леонид является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном во втором городе, используется более совершенное оборудование.

В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 4t³ часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t³ часов в неделю, они производят t приборов.

За каждый час работы (на каждом из заводов) Леонид платит рабочему 1 тысячу рублей. Необходимо, чтобы за неделю суммарно производилось 20 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?

На рисунке изображён график функции y  =  f(x), определённой на интервале (−8; 5). Найдите сумму точек экстремума функции f(x).

На рисунке изображён график функции y  =  f(x), определённой на интервале (−4; 8). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график функции y  =  f(x), определенной на интервале (−2; 10). Найдите сумму точек экстремума функции f(x).

На рисунке изображен график функции y  =  f(x), определенной на интервале (−1; 13). Найдите сумму точек экстремума функции f(x).

Всего: 15 1–15

Источник

Рассмотрим задания, в которых требуется найти промежутки убывания функции по графику производной.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-5;16). Найти промежутки убывания функции f(x). В ответ указать длину наибольшего из них.

Решение:

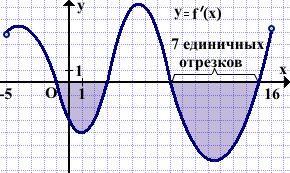
На промежутках убывания функции y=f(x) её производная y=f'(x) отрицательна.

Выделяем промежутки, на которых производная y=f'(x) принимает отрицательные значения. В данном случае таких промежутком два: (-1;3) и (8;15). Так как в точках -1, 3, 8 и 15 существует производная f'(x), то функция f(x) непрерывна в этих точках. Поэтому эти точки можно включать в промежутки возрастания и убывания. Таким образом, функция y=f(x) убывает на промежутках [-1;3] и [8;15].

Длины этих промежутков равны четырём и семи единичным отрезкам.

Ответ: 7.

№2

На рисунке изображён график функции y=f'(x) — производной функции f(x), определённой на интервале (-5;9). Найти промежутки убывания функции f(x). В ответе указать сумму целых точек, входящих в эти промежутки.

Решение:

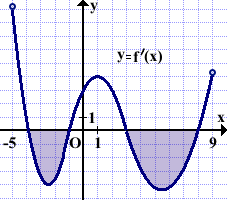
На промежутках убывания функции y=f(x) её производная y=f'(x) отрицательна.

Выделяем промежутки, на которых производная y=f'(x) принимает отрицательные значения. В данном примере таких промежутков два: (-4;-1) и (3;8).

Так как в точках -4, -1, 3 и 8 существует производная f'(x), то функция f(x) непрерывна в этих точках. Поэтому эти точки можно включить в промежутки убывания. Следовательно, функция y=f(x) убывает на промежутках [-4;-1] и [3;8].

Найдём сумму целых точек, входящих в эти промежутки:

-4+(-3)+(-2)+(-1)+3+4+5+6+7+8=23.

Ответ: 23.

№3

Функция f(x) определена и непрерывна на интервале (-6;5). На рисунке изображен график её производной. Найти промежутки убывания функции f(x). В ответе указать сумму целых точек, входящих в эти промежутки.

Решение:

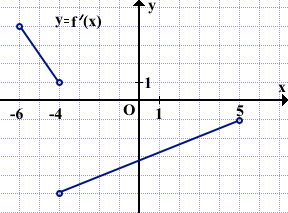
На промежутках убывания функции y=f(x) её производная f'(x) отрицательна. В данном примере производная f'(x)<0 на интервале (-4;5).

По условию, функция f(x) непрерывна на интервале (-6;5). Поэтому точку -4, входящую в этот интервал, можно включить в промежуток убывания. Таким образом, функция f(x) убывает на полуинтервале [-4;5).

Найдём сумму целых точек, входящих в промежуток [-4;5):

(-4)+(-3)+(-2)+(-1)+0+1+2+3+4=0.

Ответ: 0.

Источник

09
Авг 2013

Категория: 07 Производная, ПО

07. Применение производной к исследованию функции

2013-08-09
2023-04-30

Cледующая таблица будет весьма полезна при работе с данной темой.

Пожалуйста, будьте предельно внимательны в следующем. Смотрите, график ЧЕГО вам дан! Функции или ее производной

Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины», как в случае не интересуют нас в принципе!

Задача 1. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.

76т

Решение: + показать

Задача 2. На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Решение:+ показать

Задача 3. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Решение: + показать

Задача 4. На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых производная функции равна 0.

Решение: + показать

Задача 5. На рисунке изображён график функции и одиннадцать точек на оси абсцисс: $x_1,;x_2,;x_3,;...x_{11}$ . В скольких из этих точек производная функции отрицательна?

76е

Решение: + показать

Задача 6. На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .

Решение: + показать

Задача 7. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: + показать

Задача 8. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.

неп

Решение: + показать

Задача 9. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наибольшее значение.

Решение: + показать

Задача 10. На рисунке изображен график — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .

Решение: + показать

Задача 11. На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

e3w

Решение: + показать

Задача 12. Функция определена на промежутке На рисунке изображен график её производной. Найдите точку в которой функция принимает наименьшее значение, если

Решение: + показать

Задача 13. Функция определена и непрерывна на полуинтервале На рисунке изображен график её производной. Найдите промежутки убывания функции В ответе укажите сумму целых точек, входящих в эти промежутки.