Как найти сумму числа фибоначчи

Была ли эта статья полезной?

1. Задача Фибоначчи

Итальянский
математик Леонардо Фибоначчи жил в 13
столетии и одним из первых в Европе
стал использовать арабские (индийские)
цифры. Он придумал несколько искусственную
задачу о кроликах, которых выращивают
на ферме, причем все они считаются
самками, самцы игнорируются. Кролики
начинают размножаться после того, как
им исполняется два месяца, а потом каждый
месяц рожают по кролику. Кролики никогда
не умирают.

Нужно
определить, сколько кроликов будет на
ферме через n
месяцев, если в начальный момент времени
был только один новорожденный кролик.

Очевидно, что
фермер имеет одного кролика в первый
месяц и одного кролика – во второй
месяц. На третий месяц будет уже два
кролика, на четвертый – три и т.д.
Обозначим количество кроликов в n
месяце как
.
Таким образом,,,,,,
…

Можно построить
алгоритм, позволяющий найти
при любомn.

Согласно условию
задачи общее количество кроликов
вn+1
месяце раскладывается на три составляющие:

• одномесячные
  кролики, не способные к размножению, в
  количестве

;

• кролики, способные
  к размножению, в количестве
  ;

• новорожденные
  кролики, их количество также равно
  .

Таким образом,
получим

. (8.1)

Формула (8.1)
позволяет вычислить ряд чисел: 0, 1, 1, 2,
3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …

Числа в данной
последовательности называются числами
Фибоначчи.

Если
принять
и
,
то с помощью формулы (8.1) можно определить
все остальные числа Фибоначчи. Формула
(8.1) называется рекуррентной
формулой (recurrence
– «возвращение» на латыни).

Пример 8.1.
Предположим,
что имеется лестница в n
ступенек. Мы можем подниматься по ней
с шагом в одну ступеньку, либо – с шагом
в две ступеньки. Сколько существует
комбинаций различных способов подъема?

Если
n
= 1, имеется только один вариант решения
задачи. Для n
= 2 существует 2 варианта: два единичных
шага либо один двойной. Для n
= 3 существует 3 варианта: три единичных
шага, либо один единичный и один двойной,
либо один двойной и один единичный.

В
следующем случае n
= 4, имеем 5 возможностей (1+1+1+1, 2+1+1, 1+2+1,
1+1+2, 2+2).

Для
того чтобы ответить на заданный вопрос
при произвольном n,
обозначим количество вариантов как
,
и попробуем определитьпо известными
.
Если мы стартуем с единичного шага, то
имеем
комбинаций для оставшихсяn
ступенек. Если стартуем с двойного шага,
то имеем
комбинаций для оставшихсяn–1
ступенек. Общее количество вариантов
для n+1
ступенек равно

. (8.2)

Полученная
формула как близнец напоминает формулу
(8.1). Тем не менее, это не позволяет
отождествлять количество комбинаций

с числами Фибоначчи.
Мы видим, например, что,
но.
Однако имеет место следующая зависимость:

.

Это
справедливо для n
= 1, 2, и также справедливо для каждого n.
Числа Фибоначчи и количество комбинаций

вычисляются по одной и той же формуле,
однако начальные значения,и,у них различаются.

Пример 8.2. Этот
пример имеет
практическое
значение для задач помехоустойчивого
кодирования. Найдем число всех двоичных
слов длины n,
не содержащих несколько нулей подряд.
Обозначим это число через
.
Очевидно,,
а слова длины 2, удовлетворяющие нашему
ограничению, таковы: 10, 01, 11, т.е..
Пусть– такое слово изn
символов. Если символ
,
томожет быть произвольным ()-буквенным
словом, не содержащим несколько нулей
подряд. Значит, число слов с единицей
на конце равно.

Если же символ
,
то обязательно,
а первыесимволамогут быть произвольными с учетом
рассматриваемых ограничений. Следовательно,
имеетсяслов длины
n
с нулем на конце. Таким образом, общее
число интересующих нас слов равно

.

С учетом того, что
и,
полученная последовательность чисел
– это числа Фибоначчи.

Пример 8.3. В
примере 7.6 мы нашли, что число двоичных
слов постоянного веса t
(и длиной k)
равно
.
Теперь найдем число двоичных слов
постоянного весаt,
не содержащих несколько нулей подряд.

Рассуждать можно
так. Пусть
число нулей в рассматриваемых словах.
В любом слове имеетсяпромежутков между ближайшими нулями,
в каждом из которых находится одна или
несколько единиц. Предполагается, что.
В противном случае нет ни одного слова
без рядом стоящих нулей.

Если из каждого
промежутка удалить ровно по одной
единице, то получим слово длины
,
содержащеенулей. Любое такое слово может быть
получено указанным образом из некоторого
(и притом только одного)k-буквенного
слова, содержащего
нулей, никакие два из которых не стоят
рядом. Значит, искомое число совпадает
с числом всех слов длины,
содержащих ровнонулей, т.е. равно.

Пример 8.4. Докажем,
что сумма
равна числам Фибоначчи для любого целого.
Символобозначаетнаименьшее
целое число, большее или равное
.
Например, если,
то;
а если,
то.
По-английски эту операцию называютceil
(«потолок»). Также встречается символ
,
который обозначаетнаибольшее
целое число, меньшее или равное
.
По-английски эту операцию называютfloor
(«пол»).

Если
,
то.
Если,
то.
Если,
то.

Таким образом, для
рассмотренных случаев сумма действительно
равна числам Фибоначчи. Теперь приведем
доказательство для общего случая.
Поскольку числа Фибоначчи можно получить
с помощью рекуррентного уравнения
(8.1), то должно выполняться равенство:

.

И оно действительно
выполняется:

Здесь мы использовали
полученную ранее формулу (4.4):
.

1. Сумма чисел
   Фибоначчи

Определим
сумму первых n
чисел Фибоначчи.

0 = 0,

0+1 = 1,

0+1+1 = 2,

0+1+1+2 = 4,

0+1+1+2+3 = 7,

0+1+1+2+3+5 = 12,

0+1+1+2+3+5+8 = 20,

0+1+1+2+3+5+8+13 = 33.

Легко
заметить, что прибавлением к правой
части каждого уравнения единицы мы
снова получаем число Фибоначчи. Общая
формула для определения суммы первых
n
чисел Фибоначчи имеет вид:

.

Докажем это,
используя метод математической индукции.
Для этого запишем:

.

Эта
сумма должна быть равна
.

.

Сократив левую и
правую часть уравнения на –1, получим
уравнение (6.1).

1. Формула для
   чисел Фибоначчи

Теорема
8.1.
Числа
Фибоначчи можно рассчитать по формуле

.

Доказательство.
Убедимся в справедливости этой формулы
для n
= 0, 1, а затем докажем справедливость
данной формулы для произвольного n
по индукции. Вычислим отношение двух
ближайших чисел Фибоначчи:

Мы
видим, что отношение этих чисел колеблется
около значения 1.618 (если игнорировать
несколько первых значений). Этим свойством
числа Фибоначчи напоминают члены
геометрической прогрессии. Примем
,
().
Тогда выражение

преобразуется в

,

которое после
упрощений выглядит так

.

Мы
получили квадратное уравнение, корни
которого равны:

Теперь
можем записать:

(где
c
является константой). Оба члена
и
не дают чисел Фибоначчи,
например
,
в то время как.
Однако разность
удовлетворяет
рекуррентному уравнению:

.

Для
n=0
эта разность дает,
то есть: .
Однако при n=1
мы имеем .
Чтобы получить
,
необходимо принять:.

Теперь
мы имеем две последовательности:
и ,
которые начинаются с одинаковых двух
чисел и удовлетворяют одной и той же
рекуррентной формуле. Они должны быть
равны: .
Теорема доказана.

При
возрастании n
член
становится очень большим, в то время
как,
и роль членав разности сокращается.
Поэтому при больших n
приближенно можем записать

.

Мы
игнорируем 1/2 (поскольку числа Фибоначчи
возрастают до бесконечности при росте
n
до бесконечности).

Отношение

называется золотым
сечением,
его используют за пределами математики
(например, в скульптуре и архитектуре).
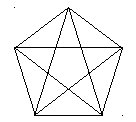
Золотым сечением является отношение
между диагональю и стороной правильного
пятиугольника
(рис. 8.1).

Рис.
8.1. Правильный пятиугольник и его
диагонали

Для обозначения
золотого сечения принято использовать
букву
в честь известного афинского скульптора
Фидия.

1. Простые числа

Все натуральные
числа, большие единицы, распадаются на
два класса. К первому относятся числа,
имеющие ровно два натуральных делителя,
единицу и самого себя, ко второму – все
остальные. Числа первого класса называют
простыми,
а второго – составными.
Простые числа в пределах первых трех
десятков: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

Свойства простых
чисел и их связь со всеми натуральными
числами изучалась Евклидом (3 век до
нашей эры). Если выписывать простые
числа подряд, то можно заметить, что
относительная плотность их убывает. На
первый десяток их приходится 4, т. е. 40%,
на сотню – 25, т.е. 25%, на тысячу – 168, т.е.
меньше 17%, на миллион – 78498, т.е. меньше
8%, и т.д.. Тем не менее, их общее число
бесконечно.

Среди простых
чисел попадаются пары таких, разность
между которыми равна двум (так называемые
простые
близнецы),
однако конечность или бесконечность
таких пар не доказана.

Евклид считал
очевидным, что с помощью умножения
только простых чисел можно получить
все натуральные числа, причем каждое
натуральное число представимо в виде
произведения простых чисел единственным
образом (с точностью до порядка
множителей). Таким образом, простые
числа образуют мультипликативный базис
натурального ряда.

Изучение распределения
простых чисел привело к созданию
алгоритма, позволяющего получать таблицы
простых чисел. Таким алгоритмом является
решето
Эратосфена
(3 век до нашей эры). Этот метод заключается
в отсеивании (например, путем зачеркивания)
тех целых чисел заданной последовательности
,
которые делятся хотя бы на одно из
простых чисел, меньших.

Теорема
8.2.
(теорема Евклида).
Число
простых чисел бесконечно.

Доказательство.
Теорему
Евклида о бесконечности числа простых
чисел докажем способом, предложенным
Леонардом Эйлером (1707–1783). Эйлер
рассмотрел произведение по всем простым
числам p:

при
.
Это произведение сходится, и если его
раскрыть, то в силу однозначности
разложения натуральных чисел на простые
сомножители получается, что оно равняется
сумме ряда,
откуда следует тождество Эйлера:

.

Так как при
ряд справа расходится (гармонический
ряд), то из тождества Эйлера следует
теорема Евклида.

Русский математик
П.Л. Чебышев (1821–1894) вывел формулу,
определяющую пределы, в которых заключено
число простых чисел
,
не превосходящихX:

,

где
,.

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted F_n . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:^[1]

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.

The Fibonacci numbers were first described in Indian mathematics,^[2][3][4] as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book Liber Abaci.^[5]

Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the Fibonacci Quarterly. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings, such as branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of an artichoke, an uncurling fern, and the arrangement of a pine cone’s bracts.

Fibonacci numbers are also strongly related to the golden ratio: Binet’s formula expresses the nth Fibonacci number in terms of n and the golden ratio, and implies that the ratio of two consecutive Fibonacci numbers tends to the golden ratio as n increases. Fibonacci numbers are also closely related to Lucas numbers, which obey the same recurrence relation and with the Fibonacci numbers form a complementary pair of Lucas sequences.

Definition[edit]

The Fibonacci numbers may be defined by the recurrence relation^[6]

and

for n > 1.

Under some older definitions, the value is omitted, so that the sequence starts with and the recurrence is valid for n > 2.^[7][8]

The first 20 Fibonacci numbers F_n are:^[1]

F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16	F17	F18	F19
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181

History[edit]

India[edit]

The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody.^[3][9][10] In the Sanskrit poetic tradition, there was interest in enumerating all patterns of long (L) syllables of 2 units duration, juxtaposed with short (S) syllables of 1 unit duration. Counting the different patterns of successive L and S with a given total duration results in the Fibonacci numbers: the number of patterns of duration m units is F_m+1.^[4]

Knowledge of the Fibonacci sequence was expressed as early as Pingala (c. 450 BC–200 BC). Singh cites Pingala’s cryptic formula misrau cha («the two are mixed») and scholars who interpret it in context as saying that the number of patterns for m beats (F_m+1) is obtained by adding one [S] to the F_m cases and one [L] to the F_m−1 cases.^[11] Bharata Muni also expresses knowledge of the sequence in the Natya Shastra (c. 100 BC–c. 350 AD).^[12][2]
However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):^[10]

Variations of two earlier meters [is the variation]… For example, for [a meter of length] four, variations of meters of two [and] three being mixed, five happens. [works out examples 8, 13, 21]… In this way, the process should be followed in all mātrā-vṛttas [prosodic combinations].^[a]

Hemachandra (c. 1150) is credited with knowledge of the sequence as well,^[2] writing that «the sum of the last and the one before the last is the number … of the next mātrā-vṛtta.»^[14][15]

Europe[edit]

The Fibonacci sequence first appears in the book Liber Abaci (The Book of Calculation, 1202) by Fibonacci^[16][17] where it is used to calculate the growth of rabbit populations.^[18][19] Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born breeding pair of rabbits are put in a field; each breeding pair mates at the age of one month, and at the end of their second month they always produce another pair of rabbits; and rabbits never die, but continue breeding forever. Fibonacci posed the puzzle: how many pairs will there be in one year?

• At the end of the first month, they mate, but there is still only 1 pair.
• At the end of the second month they produce a new pair, so there are 2 pairs in the field.
• At the end of the third month, the original pair produce a second pair, but the second pair only mate to gestate for a month, so there are 3 pairs in all.
• At the end of the fourth month, the original pair has produced yet another new pair, and the pair born two months ago also produces their first pair, making 5 pairs.

At the end of the nth month, the number of pairs of rabbits is equal to the number of mature pairs (that is, the number of pairs in month n – 2) plus the number of pairs alive last month (month n – 1). The number in the nth month is the nth Fibonacci number.^[20]

The name «Fibonacci sequence» was first used by the 19th-century number theorist Édouard Lucas.^[21]

Relation to the golden ratio[edit]

Closed-form expression[edit]

Like every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form expression. It has become known as Binet’s formula, named after French mathematician Jacques Philippe Marie Binet, though it was already known by Abraham de Moivre and Daniel Bernoulli:^[22]

where

is the golden ratio, and ψ is its conjugate:^[23]

Since , this formula can also be written as

To see the relation between the sequence and these constants,^[24] note that φ and ψ are both solutions of the equation and thus so the powers of φ and ψ satisfy the Fibonacci recursion. In other words,

It follows that for any values a and b, the sequence defined by

satisfies the same recurrence,

If a and b are chosen so that U₀ = 0 and U₁ = 1 then the resulting sequence U_n must be the Fibonacci sequence. This is the same as requiring a and b satisfy the system of equations:

which has solution

producing the required formula.

Taking the starting values U₀ and U₁ to be arbitrary constants, a more general solution is:

where

Computation by rounding[edit]

Since
for all n ≥ 0, the number F_n is the closest integer to . Therefore, it can be found by rounding, using the nearest integer function:

In fact, the rounding error is very small, being less than 0.1 for n ≥ 4, and less than 0.01 for n ≥ 8. This formula is easily inverted to find an index of a Fibonacci number F:

Instead using the floor function gives the largest index of a Fibonacci number that is not greater than F:

where , ,^[25] and .^[26]

Magnitude[edit]

Since F_n is asymptotic to , the number of digits in F_n is asymptotic to . As a consequence, for every integer d > 1 there are either 4 or 5 Fibonacci numbers with d decimal digits.

More generally, in the base b representation, the number of digits in F_n is asymptotic to

Limit of consecutive quotients[edit]

Johannes Kepler observed that the ratio of consecutive Fibonacci numbers converges. He wrote that «as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost», and concluded that these ratios approach the golden ratio ^[27][28]

This convergence holds regardless of the starting values and , unless . This can be verified using Binet’s formula. For example, the initial values 3 and 2 generate the sequence 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555, … . The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio.

In general, , because the ratios between consecutive Fibonacci numbers approaches .

Successive tilings of the plane and a graph of approximations to the golden ratio calculated by dividing each Fibonacci number by the previous

Decomposition of powers[edit]

Since the golden ratio satisfies the equation

this expression can be used to decompose higher powers as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients:

This equation can be proved by induction on n ≥ 1:

For , it is also the case that and it is also the case that

These expressions are also true for n < 1 if the Fibonacci sequence F_n is extended to negative integers using the Fibonacci rule

Identification[edit]

Binet’s formula provides a proof that a positive integer x is a Fibonacci number if and only if at least one of or is a perfect square.^[29] This is because Binet’s formula, which can be written as , can be multiplied by and solved as a quadratic equation in via the quadratic formula:

Comparing this to , it follows that

In particular, the left-hand side is a perfect square.

Matrix form[edit]

A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is

alternatively denoted

which yields . The eigenvalues of the matrix A are and corresponding to the respective eigenvectors

and

As the initial value is

it follows that the nth term is

From this, the nth element in the Fibonacci series
may be read off directly as a closed-form expression:

Equivalently, the same computation may be performed by diagonalization of A through use of its eigendecomposition:

where and
The closed-form expression for the nth element in the Fibonacci series is therefore given by

which again yields

The matrix A has a determinant of −1, and thus it is a 2 × 2 unimodular matrix.

This property can be understood in terms of the continued fraction representation for the golden ratio:

The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for φ, and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1. The matrix representation gives the following closed-form expression for the Fibonacci numbers:

For a given n, this matrix can be computed in O(log(n)) arithmetic operations, using the exponentiation by squaring method.

Taking the determinant of both sides of this equation yields Cassini’s identity,

Moreover, since AⁿA^m = A^n+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product, and one may easily deduce the second one from the first one by changing n into n + 1),

In particular, with m = n,

These last two identities provide a way to compute Fibonacci numbers recursively in O(log(n)) arithmetic operations and in time O(M(n) log(n)), where M(n) is the time for the multiplication of two numbers of n digits. This matches the time for computing the nth Fibonacci number from the closed-form matrix formula, but with fewer redundant steps if one avoids recomputing an already computed Fibonacci number (recursion with memoization).^[30]

Combinatorial identities[edit]

Combinatorial proofs[edit]

Most identities involving Fibonacci numbers can be proved using combinatorial arguments using the fact that can be interpreted as the number of (possibly empty) sequences of 1s and 2s whose sum is . This can be taken as the definition of with the conventions , meaning no such sequence exists whose sum is −1, and , meaning the empty sequence «adds up» to 0. In the following, is the cardinality of a set:

In this manner the recurrence relation

may be understood by dividing the sequences into two non-overlapping sets where all sequences either begin with 1 or 2:

Excluding the first element, the remaining terms in each sequence sum to or and the cardinality of each set is or giving a total of sequences, showing this is equal to .

In a similar manner it may be shown that the sum of the first Fibonacci numbers up to the nth is equal to the (n + 2)nd Fibonacci number minus 1.^[31] In symbols:

This may be seen by dividing all sequences summing to based on the location of the first 2. Specifically, each set consists of those sequences that start until the last two sets each with cardinality 1.

Following the same logic as before, by summing the cardinality of each set we see that

… where the last two terms have the value . From this it follows that .

A similar argument, grouping the sums by the position of the first 1 rather than the first 2 gives two more identities:

and

In words, the sum of the first Fibonacci numbers with odd index up to is the (2n)th Fibonacci number, and the sum of the first Fibonacci numbers with even index up to is the (2n + 1)st Fibonacci number minus 1.^[32]

A different trick may be used to prove

or in words, the sum of the squares of the first Fibonacci numbers up to is the product of the nth and (n + 1)st Fibonacci numbers. To see this, begin with a Fibonacci rectangle of size and decompose it into squares of size ; from this the identity follows by comparing areas:

Symbolic method[edit]

The sequence is also considered using the symbolic method.^[33] More precisely, this sequence corresponds to a specifiable combinatorial class. The specification of this sequence is . Indeed, as stated above, the -th Fibonacci number equals the number of combinatorial compositions (ordered partitions) of using terms 1 and 2.

It follows that the ordinary generating function of the Fibonacci sequence, , is the rational function

Induction proofs[edit]

Fibonacci identities often can be easily proved using mathematical induction.

For example, reconsider

Adding to both sides gives

and so we have the formula for

Similarly, add to both sides of

to give

Binet formula proofs[edit]

The Binet formula is

This can be used to prove Fibonacci identities.

For example, to prove that
note that the left hand side multiplied by becomes

as required, using the facts and to simplify the equations.

Other identities[edit]

Numerous other identities can be derived using various methods. Here are some of them:^[34]

Cassini’s and Catalan’s identities[edit]

Cassini’s identity states that

Catalan’s identity is a generalization:

d’Ocagne’s identity[edit]

where L_n is the n-th Lucas number. The last is an identity for doubling n; other identities of this type are

by Cassini’s identity.

These can be found experimentally using lattice reduction, and are useful in setting up the special number field sieve to factorize a Fibonacci number.

More generally,^[34]

or alternatively

Putting k = 2 in this formula, one gets again the formulas of the end of above section Matrix form.

Generating function[edit]

The generating function of the Fibonacci sequence is the power series

This series is convergent for any complex number satisfying and its sum has a simple closed form:^[35]

This can be proved by multiplying by :

where all terms involving for cancel out because of the defining Fibonacci recurrence relation.

The partial fraction decomposition is given by

where is the golden ratio and is its conjugate.

The related function is the generating function for the negafibonacci numbers, and satisfies the functional equation

Reciprocal sums[edit]

Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of theta functions. For example, the sum of every odd-indexed reciprocal Fibonacci number can be written as

and the sum of squared reciprocal Fibonacci numbers as

If we add 1 to each Fibonacci number in the first sum, there is also the closed form

and there is a nested sum of squared Fibonacci numbers giving the reciprocal of the golden ratio,

The sum of all even-indexed reciprocal Fibonacci numbers is^[36]

with the Lambert series since

So the reciprocal Fibonacci constant is^[37]

Moreover, this number has been proved irrational by Richard André-Jeannin.^[38]

Millin’s series gives the identity^[39]

which follows from the closed form for its partial sums as N tends to infinity:

Primes and divisibility[edit]

Divisibility properties[edit]

Every third number of the sequence is even (a multiple of ) and, more generally, every kth number of the sequence is a multiple of F_k. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property^[40][41]

where gcd is the greatest common divisor function.

In particular, any three consecutive Fibonacci numbers are pairwise coprime because both and . That is,

for every n.

Every prime number p divides a Fibonacci number that can be determined by the value of p modulo 5. If p is congruent to 1 or 4 modulo 5, then p divides F_p−1, and if p is congruent to 2 or 3 modulo 5, then, p divides F_p+1. The remaining case is that p = 5, and in this case p divides F_p.

These cases can be combined into a single, non-piecewise formula, using the Legendre symbol:^[42]

Primality testing[edit]

The above formula can be used as a primality test in the sense that if

where the Legendre symbol has been replaced by the Jacobi symbol, then this is evidence that n is a prime, and if it fails to hold, then n is definitely not a prime. If n is composite and satisfies the formula, then n is a Fibonacci pseudoprime. When m is large – say a 500-bit number – then we can calculate F_m (mod n) efficiently using the matrix form. Thus

Here the matrix power A^m is calculated using modular exponentiation, which can be adapted to matrices.^[43]

Fibonacci primes[edit]

A Fibonacci prime is a Fibonacci number that is prime. The first few are:^[44]

2, 3, 5, 13, 89, 233, 1597, 28657, 514229, …

Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.^[45]

F_kn is divisible by F_n, so, apart from F₄ = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers.

No Fibonacci number greater than F₆ = 8 is one greater or one less than a prime number.^[46]

The only nontrivial square Fibonacci number is 144.^[47] Attila Pethő proved in 2001 that there is only a finite number of perfect power Fibonacci numbers.^[48] In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that 8 and 144 are the only such non-trivial perfect powers.^[49]

1, 3, 21, and 55 are the only triangular Fibonacci numbers, which was conjectured by Vern Hoggatt and proved by Luo Ming.^[50]

No Fibonacci number can be a perfect number.^[51] More generally, no Fibonacci number other than 1 can be multiply perfect,^[52] and no ratio of two Fibonacci numbers can be perfect.^[53]

Prime divisors[edit]

With the exceptions of 1, 8 and 144 (F₁ = F₂, F₆ and F₁₂) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael’s theorem).^[54] As a result, 8 and 144 (F₆ and F₁₂) are the only Fibonacci numbers that are the product of other Fibonacci numbers.^[55]

The divisibility of Fibonacci numbers by a prime p is related to the Legendre symbol which is evaluated as follows:

If p is a prime number then

^[56][57]

For example,

It is not known whether there exists a prime p such that

Such primes (if there are any) would be called Wall–Sun–Sun primes.

Also, if p ≠ 5 is an odd prime number then:^[58]

Example 1. p = 7, in this case p ≡ 3 (mod 4) and we have:

Example 2. p = 11, in this case p ≡ 3 (mod 4) and we have:

Example 3. p = 13, in this case p ≡ 1 (mod 4) and we have:

Example 4. p = 29, in this case p ≡ 1 (mod 4) and we have:

For odd n, all odd prime divisors of F_n are congruent to 1 modulo 4, implying that all odd divisors of F_n (as the products of odd prime divisors) are congruent to 1 modulo 4.^[59]

For example,

All known factors of Fibonacci numbers F(i ) for all i < 50000 are collected at the relevant repositories.^[60][61]

Periodicity modulo n[edit]

If the members of the Fibonacci sequence are taken mod n, the resulting sequence is periodic with period at most 6n.^[62] The lengths of the periods for various n form the so-called Pisano periods.^[63] Determining a general formula for the Pisano periods is an open problem, which includes as a subproblem a special instance of the problem of finding the multiplicative order of a modular integer or of an element in a finite field. However, for any particular n, the Pisano period may be found as an instance of cycle detection.

Generalizations[edit]

The Fibonacci sequence is one of the simplest and earliest known sequences defined by a recurrence relation, and specifically by a linear difference equation. All these sequences may be viewed as generalizations of the Fibonacci sequence. In particular, Binet’s formula may be generalized to any sequence that is a solution of a homogeneous linear difference equation with constant coefficients.

Some specific examples that are close, in some sense, to the Fibonacci sequence include:

• Generalizing the index to negative integers to produce the negafibonacci numbers.
• Generalizing the index to real numbers using a modification of Binet’s formula.^[34]
• Starting with other integers. Lucas numbers have L₁ = 1, L₂ = 3, and L_n = L_n−1 + L_n−2. Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite.
• Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The Pell numbers have P_n = 2P_n−1 + P_n−2. If the coefficient of the preceding value is assigned a variable value x, the result is the sequence of Fibonacci polynomials.
• Not adding the immediately preceding numbers. The Padovan sequence and Perrin numbers have P(n) = P(n − 2) + P(n − 3).
• Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as n-Step Fibonacci numbers.^[64]

Applications[edit]

Mathematics[edit]

The Fibonacci numbers occur as the sums of binomial coefficients in the «shallow» diagonals of Pascal’s triangle:^[65]

This can be proved by expanding the generating function

and collecting like terms of .

To see how the formula is used, we can arrange the sums by the number of terms present:

5	= 1+1+1+1+1
	= 2+1+1+1	= 1+2+1+1	= 1+1+2+1	= 1+1+1+2
	= 2+2+1	= 2+1+2	= 1+2+2

which is , where we are choosing the positions of k twos from n−k−1 terms.

These numbers also give the solution to certain enumerative problems,^[66] the most common of which is that of counting the number of ways of writing a given number n as an ordered sum of 1s and 2s (called compositions); there are F_n+1 ways to do this (equivalently, it’s also the number of domino tilings of the rectangle). For example, there are F₅₊₁ = F₆ = 8 ways one can climb a staircase of 5 steps, taking one or two steps at a time:

5	= 1+1+1+1+1	= 2+1+1+1	= 1+2+1+1	= 1+1+2+1	= 2+2+1
	= 1+1+1+2	= 2+1+2	= 1+2+2

The figure shows that 8 can be decomposed into 5 (the number of ways to climb 4 steps, followed by a single-step) plus 3 (the number of ways to climb 3 steps, followed by a double-step). The same reasoning is applied recursively until a single step, of which there is only one way to climb.

The Fibonacci numbers can be found in different ways among the set of binary strings, or equivalently, among the subsets of a given set.

• The number of binary strings of length n without consecutive 1s is the Fibonacci number F_n+2. For example, out of the 16 binary strings of length 4, there are F₆ = 8 without consecutive 1s – they are 0000, 0001, 0010, 0100, 0101, 1000, 1001, and 1010. Such strings are the binary representations of Fibbinary numbers. Equivalently, F_n+2 is the number of subsets S of {1, …, n} without consecutive integers, that is, those S for which {i, i + 1} ⊈ S for every i. A bijection with the sums to n+1 is to replace 1 with 0 and 2 with 10, and drop the last zero.
• The number of binary strings of length n without an odd number of consecutive 1s is the Fibonacci number F_n+1. For example, out of the 16 binary strings of length 4, there are F₅ = 5 without an odd number of consecutive 1s – they are 0000, 0011, 0110, 1100, 1111. Equivalently, the number of subsets S of {1, …, n} without an odd number of consecutive integers is F_n+1. A bijection with the sums to n is to replace 1 with 0 and 2 with 11.
• The number of binary strings of length n without an even number of consecutive 0s or 1s is 2F_n. For example, out of the 16 binary strings of length 4, there are 2F₄ = 6 without an even number of consecutive 0s or 1s – they are 0001, 0111, 0101, 1000, 1010, 1110. There is an equivalent statement about subsets.
• Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his solving Hilbert’s tenth problem.^[67]
• The Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most.
• Moreover, every positive integer can be written in a unique way as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as Zeckendorf’s theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.
• Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, obtained from the formula

  

  The sequence of Pythagorean triangles obtained from this formula has sides of lengths (3,4,5), (5,12,13), (16,30,34), (39,80,89), … . The middle side of each of these triangles is the sum of the three sides of the preceding triangle.^[68]

• The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing.
• Fibonacci numbers appear in the ring lemma, used to prove connections between the circle packing theorem and conformal maps.^[69]

Computer science[edit]

• The Fibonacci numbers are important in computational run-time analysis of Euclid’s algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.^[70]
• Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the polyphase merge sort was described in The Art of Computer Programming.
• A Fibonacci tree is a binary tree whose child trees (recursively) differ in height by exactly 1. So it is an AVL tree, and one with the fewest nodes for a given height — the «thinnest» AVL tree. These trees have a number of vertices that is a Fibonacci number minus one, an important fact in the analysis of AVL trees.^[71]
• Fibonacci numbers are used by some pseudorandom number generators.
• Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
• A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.^[72]
• The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as μ-law.^[73][74]
• Some Agile teams use a modified series called the «Modified Fibonacci Series» in planning poker, as an estimation tool. Planning Poker is a formal part of the Scaled Agile Framework.^[75]
• Fibonacci coding
• Negafibonacci coding

Nature[edit]

Fibonacci sequences appear in biological settings,^[76] such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,^[77] the flowering of artichoke, an uncurling fern and the arrangement of a pine cone,^[78] and the family tree of honeybees.^[79][80] Kepler pointed out the presence of the Fibonacci sequence in nature, using it to explain the (golden ratio-related) pentagonal form of some flowers.^[81] Field daisies most often have petals in counts of Fibonacci numbers.^[82] In 1830, K. F. Schimper and A. Braun discovered that the parastichies (spiral phyllotaxis) of plants were frequently expressed as fractions involving Fibonacci numbers.^[83]

Przemysław Prusinkiewicz advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.^[84]

A model for the pattern of florets in the head of a sunflower was proposed by Helmut Vogel [de] in 1979.^[85] This has the form

where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat’s spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F( j):F( j + 1), the nearest neighbors of floret number n are those at n ± F( j) for some index j, which depends on r, the distance from the center. Sunflowers and similar flowers most commonly have spirals of florets in clockwise and counter-clockwise directions in the amount of adjacent Fibonacci numbers,^[86] typically counted by the outermost range of radii.^[87]

Fibonacci numbers also appear in the pedigrees of idealized honeybees, according to the following rules:

• If an egg is laid by an unmated female, it hatches a male or drone bee.
• If, however, an egg was fertilized by a male, it hatches a female.

Thus, a male bee always has one parent, and a female bee has two. If one traces the pedigree of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, F_n, is the number of female ancestors, which is F_n−1, plus the number of male ancestors, which is F_n−2.^[88] This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.

It has been noticed that the number of possible ancestors on the human X chromosome inheritance line at a given ancestral generation also follows the Fibonacci sequence.^[89] A male individual has an X chromosome, which he received from his mother, and a Y chromosome, which he received from his father. The male counts as the «origin» of his own X chromosome (), and at his parents’ generation, his X chromosome came from a single parent (). The male’s mother received one X chromosome from her mother (the son’s maternal grandmother), and one from her father (the son’s maternal grandfather), so two grandparents contributed to the male descendant’s X chromosome (). The maternal grandfather received his X chromosome from his mother, and the maternal grandmother received X chromosomes from both of her parents, so three great-grandparents contributed to the male descendant’s X chromosome (). Five great-great-grandparents contributed to the male descendant’s X chromosome (), etc. (This assumes that all ancestors of a given descendant are independent, but if any genealogy is traced far enough back in time, ancestors begin to appear on multiple lines of the genealogy, until eventually a population founder appears on all lines of the genealogy.)

Other[edit]

• In optics, when a beam of light shines at an angle through two stacked transparent plates of different materials of different refractive indexes, it may reflect off three surfaces: the top, middle, and bottom surfaces of the two plates. The number of different beam paths that have k reflections, for k > 1, is the th Fibonacci number. (However, when k = 1, there are three reflection paths, not two, one for each of the three surfaces.)^[90]
• Fibonacci retracement levels are widely used in technical analysis for financial market trading.
• Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio, the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.^[91]
• The measured values of voltages and currents in the infinite resistor chain circuit (also called the resistor ladder or infinite series-parallel circuit) follow the Fibonacci sequence. The intermediate results of adding the alternating series and parallel resistances yields fractions composed of consecutive Fibonacci numbers. The equivalent resistance of the entire circuit equals the golden ratio.^[92]
• Brasch et al. 2012 show how a generalized Fibonacci sequence also can be connected to the field of economics.^[93] In particular, it is shown how a generalized Fibonacci sequence enters the control function of finite-horizon dynamic optimisation problems with one state and one control variable. The procedure is illustrated in an example often referred to as the Brock–Mirman economic growth model.
• Mario Merz included the Fibonacci sequence in some of his artworks beginning in 1970.^[94]
• Joseph Schillinger (1895–1943) developed a system of composition which uses Fibonacci intervals in some of its melodies; he viewed these as the musical counterpart to the elaborate harmony evident within nature.^[95] See also Golden ratio § Music.

See also[edit]

• The Fibonacci Association – Organization for research on Fibonacci numbers
• Fibonacci numbers in popular culture
• Fibonacci word – Binary sequence from Fibonacci recurrence
• Random Fibonacci sequence – Randomized mathematical sequence based upon the Fibonacci sequence
• Wythoff array – Infinite matrix of integers derived from the Fibonacci sequence

References[edit]

Explanatory footnotes[edit]

Citations[edit]

Works cited[edit]

• Ball, Keith M (2003), «8: Fibonacci’s Rabbits Revisited», Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
• Beck, Matthias; Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
• Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
• Borwein, Jonathan M.; Borwein, Peter B. (July 1998), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley, pp. 91–101, ISBN 978-0-471-31515-5
• Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
• Livio, Mario (2003) [2002], The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (First trade paperback ed.), New York City: Broadway Books, ISBN 0-7679-0816-3
• Lucas, Édouard (1891), Théorie des nombres (in French), vol. 1, Paris: Gauthier-Villars.
• Sigler, L. E. (2002), Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6

External links[edit]

• Sunflowers and Fibonacci — Numberphile on YouTube
• Periods of Fibonacci Sequences Mod m at MathPages
• Scientists find clues to the formation of Fibonacci spirals in nature
• Fibonacci Sequence on In Our Time at the BBC
• «Fibonacci numbers», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• OEIS sequence A000045 (Fibonacci numbers)

Чи́сла Фибона́ччи — элементы последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

или

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS),

в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[1].

Более формально, последовательность чисел Фибоначчи задаётся линейным рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для отрицательных значений , как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что .

Происхождение[править | править вики-текст]

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая, что: изначально есть новорожденная пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?

• В начале первого месяца есть только одна новорожденная пара (1).
• В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)
• В конце второго месяца первая пара рождает новую пару и опять спаривается (2)
• В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3)
• В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)

В конце -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом:

Формула Бине[править | править вики-текст]

Формула Бине выражает в явном виде значение как функцию от n:

где  — золотое сечение. При этом и являются корнями характеристического уравнения .

Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .

Формула Бине может быть аналитически продолжена следующим образом:

При этом соотношение выполняется для любого комплексного числа z.

Тождества[править | править вики-текст]

И более общие формулы:

, а также ,

где матрицы имеют размер , i — мнимая единица.

• Числа Фибоначчи можно выразить через многочлены Чебышёва:

• Для любого n,

• Следствие. Подсчёт определителей даёт

Свойства[править | править вики-текст]

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, то есть . Следствия:

• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
• Отношения являются подходящими дробями золотого сечения и, в частности,
• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

  .

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал,^[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

  , , , .

• Производящей функцией последовательности чисел Фибоначчи является:

  

• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

  

на множестве неотрицательных целых чисел x и y.^[4]

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
• Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

  1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)

  • В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
• Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.^[5]
• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.^[6]
• Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом равно количеству таких кортежей, начинающихся с нуля, а  — начинающихся с единицы.
• Число 0,112358132134… (после запятой записаны подряд идущие числа Фибоначчи) является иррациональным.^{[источник не указан 702 дня]}

Вариации и обобщения[править | править вики-текст]

В других областях[править | править вики-текст]

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который часто оказывается неточной подгонкой под желаемый результат^[7][8].

В природе[править | править вики-текст]

• Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи. Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи^{[9][10][11][12]}
• Длины фаланг пальцев человека относятся примерно как числа Фибоначчи^[9][13].

См. также[править | править вики-текст]

• Дерево Фибоначчи
• Метод Фибоначчи с запаздываниями
• Метод Фибоначчи поиска экстремума
• Фибоначчи
• Фибоначчиева система счисления
• Числа Леонардо
• Таблица Витхоффа
• Последовательность коров Нараяны

Примечания[править | править вики-текст]

Литература[править | править вики-текст]

• Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
• А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
• А. Н. Рудаков Числа Фибоначчи и простота числа 2¹²⁷-1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
• Дональд Кнут. Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
• Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
• Грант Аракелян. Математика и история золотого сечения. — М.: Логос, 2014. — С. 404. — ISBN 978-5-98704-663-0.

Ссылки[править | править вики-текст]

	Числа Фибоначчи на Викискладе?

• Первые 300 чисел Фибоначчи (англ.)
• Расчет чисел Фибоначчи рекурсией (Mathcad Calculation Server)
• Компьютеры Фибоначчи
• Числа Фибоначчи в природе

Последовательности и ряды
Последовательности	Числовая последовательность • Фундаментальная последовательность • Линейная рекуррентная последовательность • Числа Фибоначчи • Последовательность Баркера • Последовательность де Брёйна
Ряды, основное	Сумма ряда • Остаток ряда • Условная сходимость • Мультисекция ряда
Числовые ряды (действия с числовыми рядами)	Гармонический ряд • Знакочередующийся ряд • Ряд Лейбница • Ряд Дирихле • Ряд Гранди • 1 − 2 + 3 − 4 + … • 1 + 2 + 3 + 4 + ⋯
Функциональные ряды	Ряд Тейлора • Ряд Лорана • Ряд Фурье • Тригонометрический ряд Фурье • Тригонометрический ряд • Ряд Винера
Другие виды рядов	Ряд Неймана • Ряд Пюизё
Признаки сходимости	Признаки сходимости рядов Для всех рядов Необходимое условие · Критерий Коши Для знакоположительных рядов Основной критерий · Признак сравнения · Признак Куммера · Признак Гаусса · Радикальный признак Коши · Интегральный признак · Признак Д’Аламбера · Степенной признак · Логарифмический признак · Признак Раабе · Признак Бертрана · Признак Жамэ · Признак Ермакова · Признак Лобачевского · Признак Реткеса (англ.) · Телескопический признак Для знакочередующихся рядов Признак Лейбница Для рядов вида Признак Абеля · Признак Дедекинда · Признак Дюбуа-Реймона · Признак Дирихле Для функциональных рядов Признак Вейерштрасса Для рядов Фурье Признак Дини · Признак Валле-Пуссена · Признак Жордана · Признак Юнга · Признак Салема · Признак Лебега · Признак Лебега–Гергена · Признак Марцинкевича