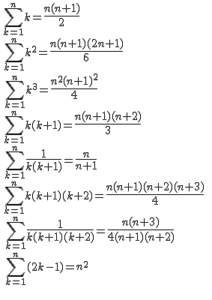Загрузить PDF
Загрузить PDF
Если вы готовитесь к тестированию или просто хотите научиться быстро складывать числа, запомните, как суммировать целые числа от 1 до 

-
1
Определите арифметическую последовательность. Посмотрите на ряд чисел, которые вы хотите сложить. Чтобы воспользоваться формулой для суммирования целых чисел, убедитесь, что ряд чисел действительно является последовательностью, то есть каждое число возрастает на одну и ту же величину.[1]
- Например, ряд чисел 5, 6, 7, 8, 9 представляет собой последовательность, как и ряд 17, 19, 21, 23, 25.
- Ряд чисел 5, 6, 9, 11, 14 не является последовательностью, потому что числа возрастают на разные величины.
-
2
-
3
Найдите количество складываемых целых чисел. Чтобы суммировать целые числа от начального числа до
, необходимо найти общее количество складываемых чисел. Например, если вы хотите сложить целые числа от 1 до 200, общее количество чисел вычисляется так: 200+1 = 201.[2]
- Например, если нужно найти сумму целых чисел от 1 до 12, количество чисел: 12+1 = 13.
-
4
Найдите сумму целых чисел между двумя целыми числами, которые в расчете не участвуют. В этом случае вычтите 1 из
.[3]
- Например, чтобы найти сумму целых чисел между 1 и 100, вычтите 1 из 100 и получите 99.
Реклама
-
1
-
2
-
3
-
4
Пользуйтесь представленными формулами, чтобы найти сумму. Когда вы подставили нужно число в формулу, умножьте его на себя, прибавьте 1, 2 или 4 (в зависимости от формулы), а затем разделите результат на 2 или 4. [7]
- Пример 1: 100*101/2 = 10100/2 = 5050.
- Пример 2 (с четными числами): 20*22/4 = 440/4 = 110.
Реклама
Об этой статье
Эту страницу просматривали 191 819 раз.
Была ли эта статья полезной?
Как найти сумму нескольких четных последовательных натуральных чисел
Автор: Ирина Гайкова
1991
Рассмотрим несколько способов вычисления суммы нескольких четных последовательных натуральных чисел
Интересная статья? Поделитесь ею пожалуйста с другими:
Хотите обучаться математике индивидуально?
Запишитесь на консультацию.
Оставьте свой комментарий:
- на Блоге
- в Вконтакте
- в Фейсбук
-
Добро пожаловать!
Ирина Гайкова — онлайн репетитор по математике.
-
Рубрики
- Алгебра 7 класс (3)
- Алгебра 8 класс (3)
- Алгебра 9 класс (16)
- Без рубрики (3)
- Видеошпаргалки алгебра (15)
- Видеошпаргалки геометрия (10)
- Видеошпаргалки математика (5)
- Видеошпаргалки физика (2)
- Вычислительные фишки (9)
- геометрия (5)
- ЕГЭ 11 класс (20)
- Задание 13 ЕГЭ. Уравнения (15)
- задачи на проценты (2)
- Справочник по началам анализа (1)
- ЕГЭ. Производная и первообразная (31)
- ЕГЭ. Стереометрия (27)
- Задачи ЕГЭ 11 класс (42)
- Движение по кругу (4)
- Задание 1 ЕГЭ математика (15)
- Задачи на арифметическую прогрессию (10)
- Задачи на среднюю скорость (4)
- Задачи на движение по прямой (25)
- Задачи на движение по реке (6)
- Задачи на производительность и работу (18)
- Задачи на сплавы (1)
- Задачи на сплавы и растворы (14)
- ОГЭ 9 класс (70)
- Задание 14 ОГЭ. Арифметическая прогрессия (5)
- Задание 20 ОГЭ. Выражения и уравнения (26)
- Задание 22 ОГЭ. Функции и графики (34)
- Задание 23 ОГЭ. Геометрическая задача на вычисление (5)
- Физика 9 класс (1)
- Финансовая математика (4)
- Задачи на вклады (3)
-
Свежие записи
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из …
Читать далее
В правильной четырехугольной пирамиде высота равна 6, боковое …
Читать далее
Стороны основания правильной четырехугольной пирамиды равны 10, боковые …
Читать далее
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, …
Читать далее
В правильной треугольной пирамиде SABC точка M − середина ребра AB, S − вершина. Известно, …
Читать далее
I think the title covers it.
Most of the formulae I’ve seen produce the sum of even or odd numbers from 1 to n. I expect I could work out how to generalise by subtracting the lower range from the higher range, eg:
For sum of odds from 49 to 157:
(Sum of all odds -> 157) — (Sum of all odds -> 45).
What I’ve heard though is there’s a general formula out of which all three problems falls, in which you give the first and last numbers and the interval between them and you’re done?
It isn’t proving easy when I’m trying to write a program that can take user input of any two values, and provide an answer every time:
Sum of odds from 1 — 99?
Sum of odds from 2 — 98?
Sum of evens from 1 — 99?
Sum of evens from 2 = 99?
Sum of evens from 3 — 3?
etc, including the sum of all numbers from 1 — 99… etc.
I’m guessing this is not a hard question and somebody will have an easy solution for it?
How would you do it?
Формулы последовательностей:
где k — порядковый номер;
n — количество членов.
Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел.
1 вариант. Для того, чтобы определить сумму 5-ти последовательных чисел, следует умножить на 5 число, находящее посередине:
(х — 2) + (х — 1) + (х) + (х + 1) + (х + 2) = 5х,
в данном выражении х — число, находящееся посередине.
Например, сумма 30 + 31 + 32 + 33 + 34 будет равна 32 х 5 = 160
2 вариант. Чтобы найти сумму 5-ти последовательных чисел, нужно:
— умножить на 5 наибольшее число;
— из полученного произведения вычесть 10.
Возьмем, к примеру, те же 5 последовательных цифр 30,31,32,33,34
Дальше: 34 х 5 = 170
170 — 10 = 160
3 вариант. Чтобы найти сумму 5 последовательных чисел, можно:
— умножить на 5 наименьшее число;
— К полученному результату прибавить 10.
Взяв в качестве примера предыдущую последовательность:
30 х 5 = 150
150 + 10 = 160
Чтобы вычислить сумму 4-х последовательных чисел, нужно:
— умножить наибольшее число на 4;
— из полученного произведения вычесть 6.
Чтобы определить сумму 6 последовательных чисел, необходимо:
— умножить на 6 наибольшее число;
— от результата отнять 15.
Чтобы рассчитать сумму 7 последовательных чисел, нужно:
— умножить на 7 наибольшее число;
— вычесть из полученного произведения 21.
Чтобы вычислить сумму 8 последовательных чисел:
— умножим на 8 наибольшее число;
— из произведения вычесть 28.
Чтобы сложить любое количество как четных, так и нечетных последовательных чисел, нужно:
— сложить первое и последнее числа последовательности;
— полученный результат делим на 2;
— затем умножаем на число последовательных чисел, что выразим формулой:
n х (a+b)/2.
Чтобы быстро и правильно рассчитать сумму последовательности, воспользуйтесь онлайн калькулятором. Для этого вам нужно лишь выбрать последовательность и число членов последовательности.
Расчет суммы последовательности из приведенных последовательностей и количества членов
Сумму четных или нечетных чисел диапазона можно подсчитать с помощью формул массива.
Если числа записаны в ячейках с A1 по A6, то тестируем на нечетность функцией ОСТАТ и вводим как формулу массива, чтобы операция умножения применялись к каждому числу.
Сумма нечетных чисел диапазона:
=СУММ( A1:A6*ОСТАТ( A1:A6*ОСТАТ( A1:A6 ;2))
Сумма четных чисел диапазона:
=СУММ( A1:A6*ОСТАТ( A1:A6*ОСТАТ( A1:A6+1 ;2))
или
=СУММ( A1:A6*ОСТАТ( A1:A6*ОСТАТ( A1:A6-1 ;2))
Эти формулы вводят в строку редактора формул как формулы массива, обязательно завершая ввод комбинацией клавиш CTRL+Shift+Enter (после этого Эксель ставит фигурные скобки вокруг формулы) .