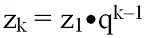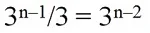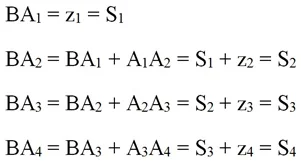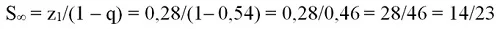Как найти сумму бесконечной геом прогрессии - AvtoShod.ru

Рассмотрим бесконечную геометрическую прогрессию b1,b2,b3…bn…

Bычислим суммы двух, трёх, четырёх и т. д. членов прогрессии:

S1=b1;S2=b1+b2;S3=b1+b2+b3…Sn=b1+b2+b3+…+bn…

Получилась последовательность S1,S2,S3…Sn…

Эта последовательность может сходиться или расходиться, как и любая другая числовая последовательность.

Если последовательность Sn сходится к пределу S, тогда число S называют суммой геометрической прогрессии (не следует путать с суммой n членов геометрической прогрессии).

В случае, когда эта последовательность расходится, то о сумме геометрической прогрессии не говорят, однако сумму первых n членов геометрической прогрессии вычислить можно.

Формула суммы первых n членов геометрической прогрессии:

если Sn=b1+b2+…+bn, то Sn=b1(qn−1)q−1.

Если знаменатель

геометрической прогрессии

(bn)

удовлетворяет неравенству

q<1

, то сумма прогрессии

существует и вычисляется по формуле

limn→∞Sn=b11−q

Источник

Формулы для нахождения суммы бесконечной геометрической прогрессии

Содержание:

Что такое геометрическая прогрессия
Бесконечная убывающая геометрическая прогрессия — что из себя представляет
Сумма первых n членов геометрической прогрессии
Как найти q в геометрической прогрессии
Примеры решения задач

Что такое геометрическая прогрессия

Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число (Xn), то говорят, что представлена числовая последовательность. Она имеет вид: (X_1, X_2)
,…,(X_n), или ({[X_n]}). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности (f(n)=X_n.)

Геометрическая прогрессия — последовательность с заданным первым членом (b_1), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число (q).

Числа ( b_1) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:

(b_n=b_{n-1}cdot q,)

Где (b_n) — (n-й) член прогрессии, (q) — знаменатель прогрессии.

Геометрическая прогрессия может быть задана рекуррентным соотношением:

(b_1=b,) (b_{n+1}=b_ncdot q,) (nin N,) (bneq0), (qneq0.)

Примечание

Рекуррентное соотношение задается формулой, выражающей (Xn) через предшествующие ему члены последовательности.

Примеры геометрических прогрессий:

1, 2, 4, 8, 16, 32 …; (b_1 = 1), (q = 2;)
1, 3, 9, 27, 81…; (b_1 = 1), (q = 3;)
2, -8, 32, -128, 512…:(b_1 = 2), (q = -4.)

Каждый член геометрической прогрессии, начиная со второго, рассчитывается как модуль среднего геометрического соседних членов:

(left|b_nright|=sqrt{b_{n-1}cdot b_{n+1}},) (ngeq2, )

или

(b_n^2=b_{n-1}cdot b_{n+1}.)

Если (b_1 > 0) и (q > 1) или (b_1 < 0) и (0 < q < 1), то для геометрической последовательности характерно возрастание.

Если (b_1 > 0) и 0 < (q < 1) или (b_1 < 0) и (q > 1), то для нее характерно убывание.

Примеры геометрических прогрессий в жизни:

Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
Начисление процентов по вкладу в банках может осуществляться по простой или сложной схеме: соответственно, проценты начисляются либо по арифметической, либо по геометрической прогрессиям.

Бесконечная убывающая геометрическая прогрессия — что из себя представляет

Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы (|q| <1.)

Сумма S всех членов бесконечной убывающей геометрической прогрессии вычисляется как соотношение между первым членом геометрической прогрессии к разности между единицей и знаменателем прогрессии:

(S=frac{b_1}{1-q}.)

Доказательством этой формулы является то, что величина (q^n) по модулю становится все меньше и меньше и стремится к нулю, при этом величина n неограниченно возрастает.

Пример такой прогрессии:

1, (frac12,) (frac14,) (frac18), (frac1{16},…)

Если (q=1), то для вычисления суммы (S_n) первых n членов геометрической прогрессии применяют следующую формулу:

(S_n=b_1+…+b_n=frac{b_1-b_nq}{1-q}=frac{b_1left(1-q^nright)}{1-q}.)

Если (q≠1), то формула видоизменяется в:

(S_n=b_1n.)

Также для объяснения формулы, введем другое обозначение суммы первых членов прогрессии:

(S_n=b_1+b_2+…+b_n.)

Тогда можно видоизменить формулу нахождения суммы (S_n) первых n членов геометрической прогрессии:

(S_n=b_1frac{q^n-1}{q-1}.)

Как найти q в геометрической прогрессии

Вычисление знаменателя прогрессии (q) осуществляют через выведение из формулы на нахождение общего члена геометрической прогрессии:

(b_n=b_1q^{n-1} )

Отсюда:

(q=frac{b_{n+1}}{b_n}.)

Примеры решения задач

Задача № 1

Сумма первого и третьего членов геометрической прогрессии равна 35. Сумма первых 5 членов в 49 раз больше суммы их обратных величин.

Найти знаменатель и первый член геометрической прогрессии.

Решение:

По условиям задачи:

(b_1+b_1q^2=35.,)

(b_1left(1+q+q^2+q^3+q^4right)=49left(frac1{b_1}+frac1{b_1q}+frac1{b_1q^2}+frac1{b_1q^3}+frac1{b_1q^4}right).) (2)

Так как (1+q+q^2+q^3+q^4neq0) (иначе задача теряет смысл), то равенство (2) можно записать в виде:

(b_1^2q^4=49. ) (3)

Из (3) следует, что либо (b_1q^2=7,) либо (b_1q^2=-7.)

Если равно 7, то из (1) находим (b_1=28,) (q^2={textstylefrac14}), откуда (q=pmfrac12 )

Если равно -7, (b_1=42,) (\q^2=-{textstylefrac16}). В этом случае второе условие задачи теряет смысл.

Конечный результат:

(b_1=28,) (q=pmfrac12. )

Задача № 2

(S_n) — сумма первых n членов геометрической прогрессии.

Доказать, что: (S_nleft(S_{3n}-S_{2n}right)=left(S_{2n}-S_nright)^2). (1)

Доказательство:

Пусть (b_k — k-й) член, (q)— знаменатель геометрической прогрессии. Тогда:

(S_{m+k}=S_m+b_1q^m+b_1q^{m+1}+…+b_1q^{m+k-1},)

откуда:

(S_{m+k}-S_m=q^mleft(b_1+b_1q+…+b_1q^{k-1}right))

или

(S_{m+k}-S_m=q^mS_k) (2).

Полагая в (2) сначала (m = 2_n,) (k = n), а затем (m = n), (k = n), получаем

(S_{3n}-S_{2n}=q^{2n}cdot S_n), (S_{2n}-S_n=q^ncdot S_n.) (3)

А из равенств (3) следует равенство (1).

Задача № 3

Сумма бесконечно убывающей геометрической прогрессии равна 4. Сумма возведенных в третью степень ее членов равна 192.

Найти первый член и знаменатель этой прогрессии.

Решение:

Обозначим: (b_1) — первый член, (S) — сумма прогрессии, (q) — знаменатель, (S_1) — сумма возведенных в третью степень ее членов.

Тогда

(S=frac{b_1}{1-q}),( S_1=frac{b_1^3}{1-q^3}.)

Далее получаем

(frac{S^3}{S_1}-frac{1-q^3}{{(1-q)}^3}=frac{4^3}{192}=frac13 )

(3(1+q+q^2)=1-2q+q^2,;qneq1..)
Полученное уравнение, записанное в виде

(2q^2+5q+2=0)

имеет корни (q_1 = −2,) (q_2 = − ½.)

Так как (|q| < 1), отбрасываем первый корень.

Следовательно:

(q=-frac12,;b_1=4(1-q)=6.)

Задача № 4

(S_n)первых трех членов геометрической прогрессии равна 351. (S_n) следующих трех членов равна 13.

Найти первый член и знаменатель прогрессии.

Решение:

Запишем условия задачи в виде системы уравнений:

(left{begin{array}{l}b_1+b_2+b_3=351,\b_4+b_5+b_6=13end{array}right.Leftrightarrow left{begin{array}{l}b_1+b_1q+b_1q^2=351,\b_1q^3+b_1q^4+b_1q^5=13end{array}right.Leftrightarrow left{begin{array}{l}b_1(1+frac13+frac19)=351,\q=frac13end{array}right.Leftrightarrowleft{begin{array}{l}frac{13}9b_1=351,\q=frac13end{array}Leftrightarrowleft{begin{array}{l}b_1=frac{351cdot9}{13}=243,\q=frac13.end{array}right.right..)

Ответ: (b_1=243,;q=frac13.)

Задача № 5

Геометрическая прогрессия содержит четное число членов. Их сумма в три раза больше суммы членов, стоящих на нечетных местах.

Найти знаменатель прогрессии?

Решение:

Определим, что в прогрессии 2n членов и (S_{2n}) — сумма всех членов, а (S_n^ast) — сумма членов, стоящих на нечетных местах.

Тогда (S_{2n}=frac{b_1(1-q^{2n})}{1-q}.)

(S_n^ast=b_1+b_3+…+b_{2n-1}=b_1+b_1q^2+…+b_1q^{2n-2}=frac{b_1(1-q^{2n)}}{1-q^2}.)

Где (b_1) — первый член прогрессии, а (q ≠ 1) — знаменатель прогрессии.

По условию задачи:

(S_{2n}=3S_n^astRightarrowfrac{b_1(1-q^{2n)}}{`1-q}=3frac{b_1(1-q^{2n)}}{1-q^2}Rightarrow1+q=3Rightarrow q=2.)

Ответ: (q=2. )

Источник

План урока:

Геометрическая прогрессия

Сумма первых n членов геометрической прогрессии

Сумма бесконечно убывающей геометрической прогрессии

Геометрическая прогрессия

Изучим послед-ть

1, 2, 4, 8, 16, 32, 64, 128…

Здесь каждый следующее число больше предыдущего в 2 раза:

1jhgjty

Подобные послед-ти именуют геометрическими прогрессиями. Они постоянно встречаются в реальной жизни в банковской сфере (при начислении процентов на вклад), при изучении демографических процессов и в ряде других дисциплин.

2gfyu

Из этого определения следует рекуррентная формула, которая задает геом. прог-сию:

3gfhf

где q – это какое-то постоянное число, которое называют знаменателем геометрической прогрессии. Так, в прог-сии

1, 2, 4, 8, 16, 32, 64, 128…

знаменатель равен 2. Чтобы найти его, достаточно поделить какой-нибудь член геометрической прогрессии на предыдущий, например:

4gfj

или

5jhkf

Если q= 0, то и все числа послед-ти, начиная со второго, получатся равными нулю:

6hfgh

Такая послед-ть не представляет интерес для математиков, поэтому считается, что знаменатель q не должен равняться нулю.

Пример. Первое число геом. прог-сии z₁ равно 10, а знаменатель q равен 3. Запишите первые пять чисел прог-сии.

Решение. Будем использовать рекуррентную формулу:

7hgfh

Итак, получаем послед-ть:

10, 30, 90, 270, 810…

Ответ: 10, 30, 90, 270, 810

Пример. Про геом. прог-сию известно, что v₁ = 16, q = 0,5. Определите семь первых чисел прог-сии.

Решение: Снова используем рекуррентную формулу:

8gfddd

Пример. Геом. прог-сия начинается с числа 27, а знаменатель q = – 1. Запишите 4 первых числа прог-сии.

Решение. Используя рекуррентную формулу, можно записать:

9hgrt

Получили послед-ть:

27, -27, 27, -27

Ответ: 27, -27, 27, -27

Попытаемся вывести формулу n-ого члена геом. прог-сии. Пусть нам известны z₁и q. Тогда можно записать:

9hgrt

Легко заметить, что числа прог-сии вычисляются по формуле:

10gdfg

Докажем ее. Для этого необходимо использовать метод индукции. Очевидно, что формула справедлива для n = 1:

11fdsfs

Здесь мы использовали тот факт, что любое число в нулевой степени равно единице, то есть q⁰ = 1.

Итак, мы доказали базис индукции. Теперь докажем ее шаг. Предположим, что формула работает для какого-то произвольного n = k:

12gfdgd

Необходимо доказать, что (n + 1)-ый член вычисляется по формуле:

13ghdh

И действительно, используя рекуррентную формулу, можно получить:

14gfdgd

Тем самым мы подтвердили справедливость формулы

15gfdgs

16ytrur

Пример. Первое число послед-ти равно 5, а каждое следующее вдвое больше. Определите 15-тый член этой послед-ти.

Решение. Описанная послед-ть является геометрической, у которой z₁ = 5, q = 2. Найдем ее 15 член:

17gfdss

Ответ: 81920.

Пример. Известно, что геом. прогрессия начинается с числа 6, а третий член – это число 216. Каким может быть второй этой прог-сии?

Решение. Сначала попробуем найти знаменатель прог-сии. Мы знаем, что z₁ = 6, z₃ = 216. Запишем формулу 2-его члена прогр-сии:

18gfdsa

Получили квадратное уравнение. Решая его можем найти возможные значений q:

19fdsa

Получили два возможных значения знаменателя. Для каждого случая определим второй член прогр-сии:

при q = – 6 получаем z₂ = z₁•q = 6•(– 6) = – 36;

при q = 6 получаем z₂ = z₁•q = 6•6 = 36.

Ответ: – 6 или 6.

Пример. Вася решил положить 1 млн рублей на банковский вклад на 1 год. В банке «Золотой гном» ему предлагают доход в 25%, который выплатят в конце года. В банке «Слон» ему предлагают выплачивать каждый месяц по 2%. Какой из вариантов выгоднее для Васи?

Решение. Напомним, что получение дохода в 25% означает увеличение суммы вклада в 1 + 25/100 = 1,25 раза. Получение 2%-ого дохода означает увеличение суммы в 1 + 2/100 = 1,02 раза.

Посчитаем, сколько у Васи будет денег через год, если он выберет банк «Золотой гном»:

20fdaa

Во втором случае сумма будет увеличиваться в 1,02 раза каждый месяц. Если выписывать суммы, лежащие на вкладе в «Слоне», то получится геом. прог-сия, у которой знаменатель равен 1,02, а первый член – миллиону

23fdssa

Тогда сумма, лежащая на вкладе через 12 месяцев, составит

24gfasd

(Примечание.Величину 1,02¹² можно посчитать на калькуляторе или компьютере.)

Получается, что второй вариант выгоднее, ведь он принесет Васе большую сумму денег.

Ответ: Лучше выбрать банк «Слон».

Пример. Дана геом. прог-сия, у которой z₁ = 5, d = 3. Может ли в этой прог-сии находиться числа: 324; 405; 406?Также проверьте числа 123456789 и 5555555555.

Решение. Первый способ (простой, но требующий большого числа расчетов). Так как каждое следующее число в прог-сии больше предыдущего в 3 раза, то мы имеем дело с возрастающей последовательностью. Будем вычислять ее члены, пока не сможем получить число, большее 406:

Получили, что число 405 входит в прог-сию (z₅ = 405), а числа 324 и 406 не входят в число первых 6 членов прог-сии. Однако, так как z₆ = 1215 больше этих двух чисел, а каждый следующий член прог-сии ещё больше, то ясно, что 324 и 406 уже не встретятся в ней. Однако проверить таким способом длинные числа довольно тяжело.

Второй способ. Каждый член последовательности можно записать в виде

26hghjd

Напомним, что если один из множителей произведения делится нацело на какое-то число, то и всё произведение делится на это же число. Множитель 3^n–1 делится на 3 (при n ≥2):

27gfdg

Число 5 делится само на себя. Следовательно, числа, входящие в эту геом. послед-ть, должны делится и на 3, и на 5.

Теперь проанализируем числа 1234546789 и 5555555555, используя признаки делимости на 3 и 5. Первое из них НЕ делится нацело на 5, так как заканчивается на 9. Число 5555555555 НЕ делится на 3, так как сумма его цифр не делится нацело на 3:

28gfsg

Значит, они не могут входить в геом. прог-сию.

Ответ: число 405 входит в прог-сию, а остальные – нет.

Сумма первых n членов геометрической прогрессии

Попытаемся вычислить сумму первых членов геом. прог-сии. Обозначим её как S_n:

29gfsdg

Умножим обе части рав-ва на знаменатель прог-сии q:

30gfdfg

Вспомним рекуррентную формулу:

31fdsg

Из нее следует, что

Тогда ур-ние (2) можно переписать так:

33gfdhg

Теперь вычтем из (3) рав-во (1)

34fhdfh

Обратите внимание – справа слагаемые z₂, z₃, z₄… z_n сначала идут со знаком «плюс», а потом – со знаком «минус». Это значит, что их можно сократить! Тогда справа останется разница z_n₊₁– z₁. Это связано с тем, что для слагаемых z_n₊₁и z₁ не нашлось противоположного числа, чтобы сократиться. Можно записать:

Далее произведем замену z_n₊₁ = z₁•qⁿ:

36gffg

Если q– 1 ≠ 0, то можно поделить обе части рав-ва и получить окончательную формулу:

37gfsdf

Отдельно рассмотрим случай, когда q– 1 = 0. Тогда полученная формула будет некорректной (будет получаться деление на ноль). Если q– 1 = 0, то q = 1. Это значит, что все члены прог-сии равны друг другу:

Тогда сумма n первых членов будет равна z₁•n:

39hgfhd

Пример. Найдите сумму первых шести членов геом. прог-сии, у которой z₁ = 3, q = 2.

Решение. Используем формулу:

41gfdfh

Ответ: 189.

Пример. Определите сумму первых пяти членов геом. послед-ти, у которой z₁ =1 и q = 1/2.

Решение. Здесь в степень придется возводить дробь 1/2:

Ответ: 31/16

Сумма бесконечно убывающей геометрической прогрессии

Легко заметить, что если знаменателем геом. прог-сии – это положительное число, которое больше единицы, то прог-сия является убывающей послед-тью. Такие последовательности называют бесконечно убывающими геометрическими прогрессиями.

В качестве примера приведем послед-ть, у которой z₁ = 1, q = 1/2:

Каждый ее член может быть рассчитан по формуле

Очевидно, что чем больше n, тем меньше z_n, причем значение z_nкак бы стремится к нулю. Например, на компьютере можно посчитать, что

То, что величина (1/2)^n–1 при больших n стремится к нулю, в математике записывается так:

46gfdf

Запись «lim» означает «предел», а символ «∞» означает бесконечность. Выражение читается так: «предел (1/2)^n–1 при n, стремящемся к бесконечности, равен нулю». Мы не будем давать строгое определение понятия «предел», так как эта задача выходит за рамки элементарной математики и относится уже к математике высшей. Грубо говоря, предел – это то число, к которому выражение приближается как угодно близко, но не может его достигнуть. Так при – 1 <q< 1 выражение qⁿстремится к нулю, если n стремится к бесконечности:

47gfdfg

Отобразим сумму первых n членов послед-ти

48hggh

с помощью координатной прямой. Пусть в точке с координатой 0 находится точка B. Отложим от нее вправо точку А₁ так, чтобы ВА₁ =z₁ = 1. Далее от точки А₁ также вправо будем откладывать точку А₂, но длина отрезка А₁А₂ будет уже вдвое меньше, то есть она составит 1/2. Будем и далее откладывать точки А₃, А₄… до какой то точки А_n:

49gfdfg

С одной стороны, длина каждого следующего отрезка будет равна члену геом. прог-сии:

C другой стороны, длина отрезков BA₁, BA₂, BA₃… будет равна сумме нескольких первых членов геом. прог-сии:

51gfdfg

Отметим, что при таком построении с увеличением n точка А_nвсё ближе приближается к числу 2, однако так и не доходит до нее. Действительно, каждая следующая точка делит оставшееся расстояние надвое, поэтому она всегда остается левее точки 2, но приближается к ней. Получается, что сумма первых n членов прог-сии c ростом n приближается к двойке. В математике говорят, что число 2 является пределом послед-ти S_n. Запишем это:

На рисунке мы рассмотрели поведение послед-ти, у которой q = 1/2. Однако оказывается, что и любая другая бесконечная убывающая геометрическая прогрессия ведет себя похожим образом. Для каждой такой послед-ти существует предел суммы ее членов. Покажем, как его найти.

Запишем формулу суммы n членов геом. прог-сии в более удобном дробном виде:

53gfdfg

Умножим и числитель, и знаменатель одновременно на (– 1), при этом можно будет поменять местами уменьшаемое и вычитаемое:

54gdfgd

Далее выделим целую часть:

55gfdgs

Проанализируем полученное выражение. Уменьшаемое z₁/(1 – q) не содержит переменной n, а потому не зависит от этой переменной. А вот вычитаемое содержит множитель qⁿ. Можно доказать, что если выполняется условие–1 <q< 1, то с ростом n этот множитель стремится к нулю:

Значит, и всё вычитаемое также стремится к нулю:

57gfdfg

Получается, что при, бесконечно большом значении n сумма S_∞может быть вычислена так:

58gfdfh

Итак, удалось получить формулу S_∞ = z₁/(1 – q). Ещё раз отметим, что по-настоящему строгое доказательство требует использование понятие предела из высшей математики, а потому не рассматривается здесь.

59hgfh

60gfdgd

Зачем вообще находить сумму бесконечной геометрической прогрессии? Оказывается, что такая задача встает при изучении ряда других разделов математики, а также при расчете вероятностей некоторых событий.

Пример. Найдите сумму S_∞ для прог-сии, у которой z₁ = 0,1, q = 0,1.

Решение. Запишем первые несколько членов прог-сии:

61gfdgf

Теперь будем записывать суммы S_n этой прог-сии:

62gfdgd

Очевидно, что при бесконечном n получается бесконечная периодическая дробь:

63gfdfg

Подробнее о бесконечных периодических дробях можно узнать из этого урока.

Теперь найдем сумму S_∞, используя формулу S_∞ = z₁/(1 – q):

64hgfgh

Получили дробь 1/9. Получается, что обыкновенная дробь 1/9 и бесконечная периодическая дробь 0,(1) – это одно и то же число! И действительно, если на калькуляторе поделить 1 на 9, то он покажет 0,111111111…:

Пример. Какая дробь при разложении ее в бесконечную десятичную дробь дает число 0,010101010101 = 0,(01)?

Решение: По аналогии с предыдущей задачей можно записать:

0,(01) = 0,01010101… = 0,01 + 0,0001 + 0,000001 + 0,00000001…

Получили слева сумму бесконечной прог-сии

в которой z₁ = 0,01, а знаменатель q = 0,01. Ее сумма может быть рассчитана по формуле:

67gfdfg

Получили дробь 1/99. То есть

68hgfgh

Проверим себя с помощью калькулятора:

69gfdgh

Пример. В квадрат со стороной 1 вписали другой квадрат, причем его вершины располагаются на серединах описанного квадрата. По тому же принципу в полученный квадрат вписали следующий квадрат, в него ещё один и т. д. Чему равна общая площадь всех полученных квадратов и каков их общий периметр?

70gfdg

Решение. Сторона первого квадрата равна 1. Найдем сторону вписанного треугольника:

71gfdgd

Изучим треугольник АВС. В нем АВ = ВС = 1/2 (ведь они составляют половину от сторон DB и BF, который по условию равны 1). Угол АВС – прямой, а потому можно воспользоваться теоремой Пифагора:

Получили, что сторона вписанного квадрата в √2 раз меньше, чем сторона исходного квадрата. Аналогично можно показать, что и у следующего квадрата сторона будет ещё в √2 раз меньше и т. д. Соответственно и периметры квадратов будут уменьшаться в √2 раз, при этом периметр первого квадрата равен 4•1 = 4.

Получаем, что периметры квадратов образуют убывающую геом. прог-сию, в которой

73gfhgh

Найдем сумму S_∞для этой прог-сии:

74gfdgd

Итак, общий периметр найден. Теперь найдем сумму площадей. Площадь исходного квадрата равна 1•1 = 1. Площадь вписанного квадрата составляет:

75hfdgh

Получили, что площадь вписанного квадрата вдвое меньше площади исходного. Тогда площади квадратов образуют геом. прог-сию, в которой

Найдем и для этой прог-сии сумму:

Итак, суммарная площадь всех квадратов равна двум.

Наконец, рассмотрим задачу, имеющую практическое содержание.

Пример. Два спортсмена, Вася и Петя, играют в настольный теннис. Счет в их партии равен 10:10, и поэтому у них действует правило «баланса». Согласно нему, игроки при равном счете должны разыграть два очка, причем в первом розыгрыше подавать будет Вася, а во втором – Петя. Если одному игроку удастся выиграть оба очка, то он выиграет всю партию. Если каждый из игроков выиграет по одному розыгрышу, то счет в их партии становится равным, и тогда им снова надо разыгрывать ещё два очка. Проще говоря, партия не закончится, пока разница в счете не составит два очка.

Известно, что при подаче Васи вероятность его победы в розыгрыше составляет 0,7. При подаче Пети шансы подающего на выигрыш очка равны 0,6. Каковы шансы Васи и Пети на победу в партии?

Решение. По условию начальный счет равен 10:10. Будем считать, что первое число в счете – это очки Васи,а второе – очки Пети. Игра закончится победой одного из игроков, когда его преимущество в счете достигнет 2 очков. Тогда возможные варианты развития событий можно изобразить с помощью схемы:

79gfdgf

Обратим внимание, что в игре возможно бесконечное количество вариантов развития событий. Так, окончательный счет может быть равен даже 102:100 или 100002:100000 (хотя это и крайне маловероятно). Пусть вероятность, что игра закончится, например, со счетом 15:13, будет обозначаться как Р_15:13. Тогда, чтобы найти вероятность победы Васи, надо сложить бесконечное число вероятностей:

80gfdgf

Первую подачу при счете «ровно» Вася выиграет с вероятностью 0,7, поэтому шансы Пети забрать 1-ое очко себе равны 1 – 0,7 = 0,3.

На второй подаче Петя выиграет с вероятностью 0,6, а шансы Васи составят 1 – 0,6 = 0,4.

Тогда вероятность, что Вася выиграет оба очка, составит

81fsdf

Для Пети вероятность забрать себе оба очка равна

82gfdfg

Есть и третий вариант развития событий – после двух розыгрышей счет останется равным (каждый выиграет один мяч), и снова возникает «баланс». Вероятность такого исхода равна

83gdfg

Следовательно, можно записать:

84gdfg

Счета 13:11, 12:12 и 11:13 могут наступить только в том случае, если сначала был достигнут счет 11:11. «Переход» из счета 11:11 к счету 13:11 произойдет, если Вася выиграет два очка подряд, а вероятность такого исхода мы уже считали: Р_в = 0,7•0,4 = 0,28. Поэтому можно записать

85gdfgd

Аналогично для счетов 12:12 и 11:13 запишем:

Следующие три счета, 14:12, 13:13 и 12:14, возможны только после счета 12:12. Их вероятности записываются так:

По аналогии для счетов 15:13, 14:14 и 13:15 можно записать:

Такие записи можно продолжать бесконечно. Однако легко увидеть, что вероятности счетов, победных для Васи, образуют геом. прог-сию:

89gfdfg

Её первый член равен 0,28, а знаменатель составляет 0,54. Тогда сумма всех этих вероятностей, а значит и общая вероятность победы Васи, составит

Аналогично и счета, выигрышные для Пети, образуют геом. прог-сию:

Здесь z₁ = 0,18; q = 0,54. Найдем сумму геометрической прогрессии:

Проверим себя. Ясно, что партию выиграет либо Вася, либо Петя. То есть сумма вероятностей их побед должна равняться единице. И действительно:

Значит, наши расчеты верны.

Ответ: Вася выиграет с вероятностью 14/23, а шансы Пети равны 9/23.

Источник

16
Июл 2013

Категория: Справочные материалы

Геометрическая прогрессия

2013-07-16
2021-06-28

А вы знаете удивительную легенду о зернах на шахматной доске? + показать

Определение

Геометрическая прогрессия — последовательность чисел (членов прогрессии) , в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии):

, где

Например, последовательность 1, 2, 4, 8, 16, … – геометрическая ()

Геометрическая прогрессия

Знаменатель геометрической прогрессии

$q=frac{b_{k+1}}{b_k}$ ,

Характеристическое свойство геометрической прогрессии

$b_n^2=b_{n-1}cdot b_{n+1}$ для

Последовательность является геометрической тогда и только тогда, когда для любого n > 1 выполняется указанное выше соотношение.

В частности, для геометрической прогрессии с положительными членами, верно: $b_n=sqrt{b_{n-1}cdot b_{n+1}}$

Формула n-го члена геометрической прогрессии

$b_n=b_1cdot q^{n-1}$

Сумма n первых членов геометрической прогрессии

$S_n=frac{b_1(q^n-1)}{q-1}$ , где

(если же , то )

Бесконечно убывающая геометрическая прогрессия

При , геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число $S=lim_{nto infty}S_n$ и $S=frac{b_1}{1-q}$

Посмотри это видео

Примеры

Пример 1. Последовательность {} –геометрическая прогрессия.

Найдите , если $b_6=-frac{1}{81}$ , $q=-frac{1}{9}.$

Решение: + показать

Приметр 2. Найдите знаменатель геометрической прогрессии {}, в которой $b_8=172,;b_{11}=2frac{11}{16}.$

Решение: + показать

Пример 3. Найдите девятый член геометрической прогрессии, если ее десятый член равен , а одиннадцатый член равен

Решение: + показать

Пример 4. Найдите сумму первых шести членов геометрической прогрессии

Решение: + показать

Пример 5. Найдите сумму первых пяти членов геометрической прогрессии {}, в которой $b_3=frac{1}{2},;b_5=2,;q>0.$

Решение: + показать

Пример 6. Представьте в виде обыкновенной дроби число

Решение: + показать

Пример 7. Найдите , если известно, что числа являются последовательными членами геометрической прогрессии (в указанном порядке).

Решение: + показать

Пример 8. Найдите знаменатель геометрической прогрессии, отношение суммы первых четырех членов которой, к сумме первых двух членов равно $frac{82}{81}.$

Решение: + показать

Пример 9. Между числами и вставьте три числа так, чтобы получилась геометрическая прогрессия

Решение: + показать

Вы можете пройти тест по теме «Геометрическая прогрессия»

Автор: egeMax |

комментариев 5

Печать страницы

Источник

Содержание

Определение геометрической прогрессии
- Формула n-го члена геометрической прогрессии
Сумма первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии
Сумма бесконечно убывающей геометрической прогрессии

Определение геометрической прогрессии

Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.

То есть геометрическая прогрессия определяется рекуррентным соотношением

$[b_{n+1} = b_n cdot q.]$

Теорема 1. Пусть — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула

$[b_n = b_1cdot q^{n-1}.]$

Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:

$[b_n = b_{n-1}q = b_{n-2}q^2 = ldots = b_1q^{n-1}.]$

Итак, для n-го члена геометрической прогрессии справедлива формула

$[b_n = b_1cdot q^{n-1}.]$

Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:

$[b_n^2 = b_{n-1}cdot b_{n+1}.]$

Доказательство. Из определения геометрической прогрессии

$[b_n = b_{n-1}cdot q, qquad b_{n+1} = b_n cdot q.]$

Следовательно,

$[frac{b_n}{b_{n-1}} = frac{b_{n+1}}{b_n} = q,]$

откуда

$[b_n^2 = b_{n-1}cdot b_{n+1}.]$

Обратное утверждение тоже верно. Если для всех членов последовательности ${b_n},$ начиная со второго, выполняется равенство $b_n^2 = b_{n-1}cdot b_{n+1},$ то эта последовательность — геометрическая прогрессия.

Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.

Решение. По условию

$begin{equation*} begin{cases} b_1 + b_3 = 10, \ b_2 + b_4 = 30. end{cases} end{equation*}$

Выразим члены геометрической прогрессии через и : Тогда система запишется в виде

$begin{equation*} begin{cases} b_1 + b_1q^2 = 10, \ b_1q + b_1q^3 = 30. end{cases} end{equation*}$

Разделив второе уравнение системы на первое, получим Следовательно,

Сумма первых n членов геометрической прогрессии

Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :

(1) $begin{equation*}S_n= b_1 + b_2 + ldots + b_n.end{equation*}$

Умножим это равенство на :

или

(2) $begin{equation*}S_n q = b_2 + b_3 + ldots + b_{n+1}.end{equation*}$

Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим $S_n q - S_n = b_{n+1} - b_1.$ Отсюда, так как имеем

$[S_n = frac{b_{n+1} - b_1}{q - 1},]$

или

(3) $begin{equation*}S_n = frac{b_nq - b_1}{q - 1}.end{equation*}$

Так как $b_n = b_1q^{n-1},$ то формулу (3) можно переписать в виде

(4) $begin{equation*}S_n = frac{b_1(q^n - 1)}{q - 1}.end{equation*}$

Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.

Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?

Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии

$[1, 2, 2^2, 2^3, ldots , 2^{63}.]$

По формуле (3) получаем

$[S = frac{2^{63}cdot 2 - 1}{2 - 1} = 2^{64} - 1 = ]$

Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.

Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.

Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.

Сумма бесконечно убывающей геометрической прогрессии

Рассмотрим геометрическую прогрессию ${b_1q^{n-1}}.$ Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.

Сумма бесконечно убывающей геометрической прогресcии выражается формулой

(5) $begin{equation*}S = frac{b_1}{1 - q}.end{equation*}$

Пример 3. Найдём сумму

$[S = frac{1}{2} - frac{1}{4} + frac{1}{8} - frac{1}{16} + ldots.]$

Решение. — сумма бесконечно убывающей геометрической прогрессии с первым членом $b_1 = frac{1}{2}$ и знаменателем $q = -frac{1}{2}.$ По формуле (5) получаем