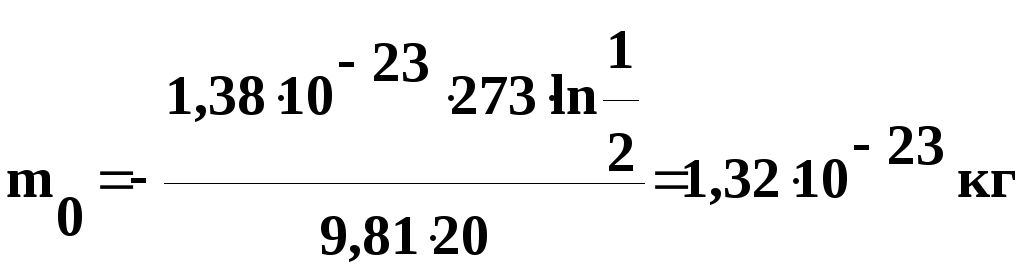Как найти суммарную кинетическую энергию газа - AvtoShod.ru

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,663
гуманитарные
33,654
юридические
17,917
школьный раздел
611,987
разное
16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Уравнение состояния идеального газа

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна m_0 . Кинетические энергии частиц:

$E_1=frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}, E_2=frac{displaystyle m_0 v_2^2 }{displaystyle 2 vphantom{1^a}}, ldots,E_N=frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}}.$

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

$E=frac{displaystyle E_1+E_2+ ldots+E_N}{displaystyle N vphantom{1^a}}= frac{displaystyle 1}{displaystyle N vphantom{1^a}}left ( frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}+frac{displaystyle m_0 v_2^2}{displaystyle 2 vphantom{1^a}}+ ldots + frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}} right ) =frac{displaystyle m_0}{displaystyle 2 vphantom{1^a}} frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Последний множитель — это средний квадрат скорости, обозначаемый просто v_2 :

$v_2=frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Тогда формула для средней кинетической энергии приобретает привычный вид:

$E=frac{displaystyle m_0 v^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

$v=sqrt{ frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}}.$

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

$p= frac{displaystyle 2}{displaystyle 3 vphantom{1^a}} nE.$ (2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} m_0 nv^2.$ (3)

Что такое m_0n ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} rho v^2.$ (4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

$E= frac{displaystyle 3}{displaystyle 2 vphantom{1^a}} kT,$ (5)

где $k=1,38 cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

• Основное уравнение
кинетической теории газов

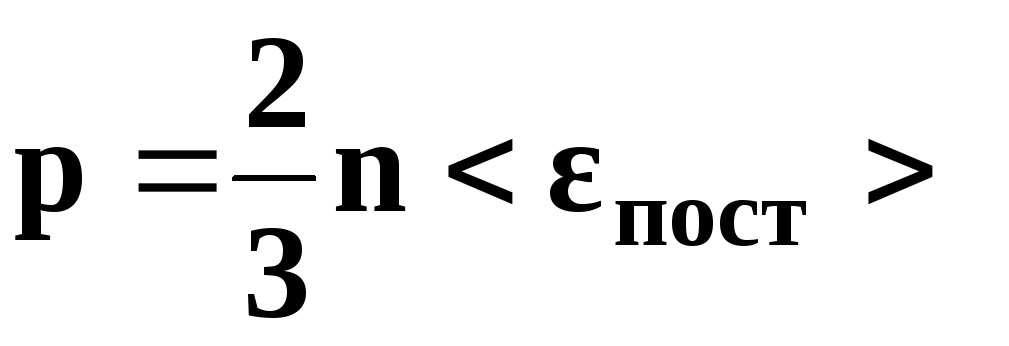
где
р — давление
газа, n
– концентрация
молекул (число молекул в единице объема),
—
средняя кинетическая энергия
поступательного движения одной молекулы,
угловые скобки обозначают осреднение
по

большому
ансамблю частиц, m₀– масса
молекулы,
—
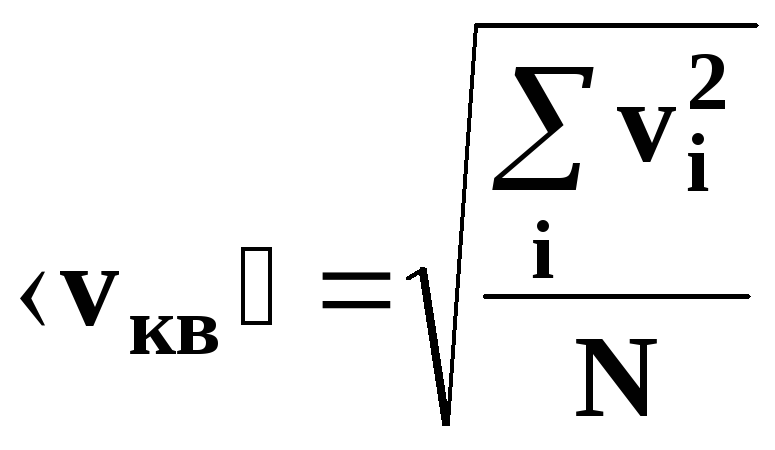
средняя квадратичная скорость движения
молекул.

• Средняя
кинетическая энергия поступательного
движения одной молекулы

где
k
=
1,38·10^-23
Дж/К –
постоянная Больцмана, Т
– абсолютная температура.

•
Энергия теплового
движения молекул (внутренняя энергия
идеального газа):

где
i
– число степеней свободы молекулы, m
– масса газа, М
– молярная
масса данного вещества, R
= 8,31 Дж/(кг·К) –
универсальная газовая постоянная, Т
– абсолютная
температура.

• Числом степеней
свободы называется число независимых
координат полностью определяющих
положение тела в пространстве. Любая
молекула имеет 3 поступательных степени
свободы (i_пост=3).
Молекулы,
кроме одноатомных, имеют еще вращательные
степени свободы (у двухатомных молекул
i_вр
= 2, у
многоатомных i_вр
= 3) и
колебательные степени свободы, которые
при невысоких (комнатных) температурах
не учитываются.

• В соответствии
с законом Больцмана о равномерном
распределении энергии по степеням
свободы, в
среднем на каждую степень свободы
молекулы приходится одинаковая энергия,
равная
.

• Средняя
кинетическая энергия вращательного
движения одной молекулы:

•
Средняя суммарная
кинетическая энергия одной молекулы:

где
i
– число степеней свободы молекулы
(i=i_пост+
i_вр).

• Средняя
квадратичная скорость молекулы:

• Средняя
арифметическая скорость (средняя
скорость теплового движения)молекулы:

где m₀
– масса одной молекулы, М
– молярная масса вещества, причем
,

N_A=
6,023·10²³
1/моль –
число Авогадро.

• Барометрическая
формула характеризует изменение давления
газа с высотой в поле сил тяжести:

или
,

где
p
– давление
на высоте h
над уровнем
моря, p₀
– давление на высоте h
= 0,
g
– ускорение
свободного падения. Эта формула
приближенная, так как температуру нельзя
считать постоянной для большой разности
высот.

•
Распределение
Больцмана для концентрации частиц в
силовом поле имеет вид:

где
n
– концентрация частиц, обладающих
потенциальной энергией W_п
, n₀
— концентрация
частиц в точках поля с W_п
= 0.

Примеры
решения задач

Задача
1. Найти
среднюю кинетическую энергию
вращательного движения одной молекулы
кислорода при температуреТ
= 350 К, а также среднюю кинетическую
энергию
вращательного движения всех молекул
кислорода массойm
= 4 г.

Решение.
Согласно закону Больцмана о равном
распределении энергии по степеням
свободы на каждую степень свободы
приходится энергия равная
,
гдеk
– постоянная Больцмана, Т
– абсолютная
температура.

Так
как молекула кислорода двухатомная, у
нее две вращательных степени свободы,
поэтому средняя кинетическая энергия
вращательного движения выразится
формулой:

Подставим
в полученную формулу значения k
= 1,38·10^-23
Дж/К, и Т
= 350 К, получим

Кинетическая
энергия всех N
молекул, содержащихся в 4 г кислорода
равна:

Число
всех молекул газа можно вычислить по
формуле:

,
где N_A
– число
Авогадро,
—
количество вещества,m
– масса газа, М
– молярная
масса. Учтя приведенные выражения,
получим:

Подставляем
числовые значения: N_A
= 6,023·10²³
1/моль ; m
= 4 г = 4·10^-3
кг ; М
= 32·10^-3
кг/моль;
=
4,83·10^-21
Дж:

Выведем
размерность полученной величины:

Задача
2. В
воздухе при нормальных условиях взвешены
одинаковые частицы. Известно, что
концентрация частиц уменьшается в два
раза на высоте h
= 20 м. Определить массу частицы.

Решение.
Воспользуемся формулой распределения
Больцмана:

где
W_п
= m₀gh
– потенциальная
энергия частицы в поле сил тяжести.

Подставив
это выражение в формулу распределения
Больцмана, получим:

Логарифмируем
обе части уравнения по основанию е,
тогда:

,
откуда

Подставив
числовые значения в полученную формулу,
найдем

Выведем
размерность полученной величины:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Виктор Матвеевич Скоков

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Количество независимых переменных, которыми определяется состояние системы, называют числом степеней свободы. Для полной характеристики энергетического состояния движения материальной точки в момент времени t требуется задать три компоненты скорости для того, чтобы определить кинетическую энергию и три координаты, чтобы определить потенциальную энергию, получается всего необходимо шесть переменных. В случае динамического рассмотрения движения материальной точки эти переменные являются зависимыми. Статистическая система, которая состоит из n точек, имеет 6n степеней свободы. Из них 3n степеней свободы — носители кинетической энергии и 3n — носители потенциальной энергии, если система находится в поле внешних сил или частицы взаимодействуют между собой.

Степени свободы

Степени свободы делят на: поступательные, вращательные и колебательные. Три степени свободы материальной точки — поступательные. Система из n материальных точек, между которыми нет жестких связей имеет 3 n степени свободы. Каждая жесткая связь уменьшает число степеней свободы на единицу. Рассмотрим молекулу, состоящую из двух атомов, если считать, что между атомами существует одна жесткая связь, то такая молекула имеет пять степеней свободы, три поступательные и две вращательные. Если связь квазиупругая, то степеней свободы будет шесть, причем из них три поступательные, две вращательные и одна колебательная. Трехатомной нелинейной молекуле с жесткой связью между атомами нужно приписать шесть степеней свободы — три поступательные, три вращательные. Поступательные степен свободы не имеют преимуществ друг перед другом.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Средняя энергия молекулы

Согласно закону равномерного распределения энергии по степеням свободы на каждую степень свободы в среднем приходится одинаковая кинетическая энергия равная $leftlangle {varepsilon }_irightrangle =frac{1}{2}kT$. В таком случае можно сказать, что средняя энергия молекулы $leftlangle {varepsilon } rightrangle$ равна:

где $i=m_{post}+m_{vr}+2m_{kol}$- сумма числа поступательных, вращательных и удвоенного количества колебательных степеней свободы, $k$ — постоянная Больцмана, T- термодинамическая температура. Возникновение коэффициента 2 при подсчёте энергии колебаний объясняется просто: При колебаниях частица имеет как кинетическую, так и потенциальную энергии. Если колебания гармонические, то эти энергии в среднем равны друг другу. Соответственно, $leftlangle {varepsilon }_{kol}rightrangle =kT$.

Закон равномерного распределения энергии по степеням свободы является приближенным, так как получен на основе классической механики и нарушается, если существенными становятся квантовые эффекты.

«Энергия молекул» 👇

Необходимо отметить, что поступательно могут двигаться только молекулы газов.

Из(1) следует, что одноатомные молекулы имеют среднюю кинетическую энергию:

Полную энергию i частицы можно представить:

[{varepsilon }_i=frac{1}{2}m_i{v_i}^2+frac{1}{2}left(J_{i1}{w_{i1}}^2+J_{i2}{w_{i2}}^2+J_{i3}{w_{i3}}^2right)+sumlimits_j{frac{m_{ij}{{eta }_{ij}}^2}{2}}+sumlimits_j{frac{k_{ij}{{xi }_{ij}}^2}{2}}+U_ileft(x_i,y_i,z_iright) left(3right),]

где $U_ileft(x_i,y_i,z_iright)$- потенциальная энергия сложной частицы во внешних полях, ${xi }_{ij}$- отклонение от положения равновесия частицы при колебаниях, ${eta }_{ij}$- скорость колебательных движений частицы, первый индекс обозначает номер сложной частицы, второй определяет номер частицы внутри сложной, $v_i$ — скорость центра масс сложной частицы, $m_i$- масс частицы, $J_1,J_2,J_3$- моменты инерции вращения частицы, $w_1,w_2,w_3$ — угловые скорости вращения частицы относительно ее главных осей. Индекс j принимает столько значений, сколько необходимо, чтобы исчерпать все степени свободы сложной частицы.

Пример 1

Задание: Сравните средние энергии молекул кислорода и азота при одинаковых температурах.

Решение:

Кислород имеет двухатомную молекулу ($O_2)$, предположим, что связь между атомами жесткая, следовательно, молекула кислорода обладает пятью степенями свободы (тремя поступательными и двумя вращательными). Из закона равномерного распределения энергии по степеням свободы имеем средняя энергия молекулы:

[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle {varepsilon }_{O_2}rightrangle =frac{5}{2}kT left(1.1right)]

Азот имеет двухатомную молекулу ($N_2)$, предположим, что связь между атомами жесткая, следовательно, молекула азота также обладает пятью степенями свободы. Соответственно:

[leftlangle {varepsilon }_{N_2}rightrangle =frac{5}{2}kTleft(1.2right).]

Ответ: Средние энергии молекул кислорода и азота при одинаковых температурах одинаковы.

Пример 2

Задание: Водород находится в сосуде при температуре T=300K. Определите среднюю энергию вращательного движения молекул.

Решение:

Основой для решения задачи является закон равномерного распределения энергии по степеням свободы. Из него известно, что на каждую степень свободы приходится в среднем энергия $leftlangle {varepsilon }_irightrangle $, равная:

[leftlangle {varepsilon }_irightrangle =frac{1}{2}kT left(2.1right).]

Следовательно, чтобы решить задачу, осталось определить, сколько вращательных степеней свободы имеет молекула водорода. Для этого вспомним химическую формулу водорода:

[H_2.]

В молекуле имеется два атома, если молекула жесткая, то общее число степеней свободы такой молекулы будет равно пяти. Из них три приходятся на поступательные степени свободы, на вращательные степени свободы остается две степени. Соответственно:

[leftlangle {varepsilon }_{vr}rightrangle =frac{2}{2}kT=kTleft(2.2right)]

Проведем расчет:

[leftlangle {varepsilon }_{vr}rightrangle =1,38cdot {10}^{-23}cdot 300=4,14cdot {10}^{-21}(Дж)]

Ответ: Средняя энергия вращательного движения молекул водорода при заданных условиях равна $4,14cdot {10}^{-21}Дж$.

Пример 3

Задание: Чему равна суммарная средняя кинетическая энергия молекул двухатомного газа, заключенного в объеме 4 л при давлении 1,47 $cdot {10}^5$Па? Молекулы считать жесткими.

Решение:

Жесткие двухатомные молекулы имеют пять степеней свободы. Средняя энергия движения молекулы определяет формула:

[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle varepsilon rightrangle =frac{5}{2}kTleft(3.1right).]

Следовательно кинетическая энергия всех N молекул газа может быть найдена, как:

[leftlangle Erightrangle =frac{5}{2}NkT left(3.2right).]

Из уравнения состояния идеального газа:

[p=nkT, где n=frac{N}{V}to pV=NkTleft(3.3right).]

Подставим в (3.2) уравнение из (3.3), получим:

[leftlangle Erightrangle =frac{5}{2}pV left(3.4right).]

Переведем данные в СИ: V=4 л=4$cdot {10}^{-3}м^3$

Проведем расчет:

[leftlangle Erightrangle =frac{5}{2}1,47 cdot {10}^5cdot 4cdot {10}^{-3}=1470 (Дж)]

Ответ: Суммарная средняя кинетическая энергия молекул двухатомного газа при заданных условиях равна $1470 Дж.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Перейти к контенту

Условие задачи:

Каким выражением определяется суммарная кинетическая энергия поступательного движения всех молекул в одном моле идеального газа при температуре (T)?

Задача №4.1.74 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(T), (E-?)

Решение задачи:

Кинетическая энергия поступательного движения одной молекулы идеального газа (E_{к}) определяется по формуле:

[{E_к} = frac{3}{2}kT]

Известно, что в 1 моль вещества содержится молекул, число которых равно числу Авогадро (N_А). Значит суммарная кинетическая энергия молекул (E), содержащихся в 1 моле, больше кинетической энергии одной молекулы (E_{к}) в (N_А) раз:

[E = {N_А}{E_к}]

Тогда:

[E = frac{3}{2}k{N_А}T]

Произведение постоянной Больцмана (k) на число Авогадро (N_А) даёт в результате универсальную газовую постоянную (R):

[R = k{N_А}]

В итоге получим такое выражение:

[E = frac{3}{2}RT]

Ответ: (frac{3}{2}RT).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.73 Если температура идеального газа возрастает в 2 раза, то как изменяется среднеквадратичная
4.1.75 В 1 дм3 объема при давлении 10^5 Па находятся 3×10^21 молекул кислорода (молярная
4.2.1 Какой объем занимает 1 кг кислорода при 0 C и давлении 800 кПа?

( 3 оценки, среднее 5 из 5 )

Источник

Уравнение состояния идеального газа

Средняя кинетическая энергия частиц газа

Основное уравнение МКТ идеального газа

Энергия частиц и температура газа

Степени свободы

Средняя энергия молекулы

Условие задачи:

Дано:

Решение задачи:

Ответ: (frac{3}{2}RT).

Смотрите также задачи:

Не пропустите также: