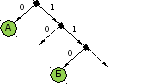
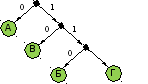
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М — кодовое слово 01. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Примечание.
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Урок посвящен тому, как решать 4 задание ЕГЭ по информатике
Содержание:
- Кодирование информации
- Кодирование и расшифровка сообщений
- Решение 4 заданий ЕГЭ
Кодирование информации
4-е задание: «Кодирование и декодирование информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 2 минуты.
Проверяемые элементы содержания: Умение кодировать и декодировать информацию
До ЕГЭ 2021 года — это было задание № 5 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Из-за невнимательного чтения условия задания экзаменуемые иногда не замечают, что требуется найти кодовое слово минимальной длины с максимальным (минимальным) числовым значением.
Кроме того, если в задании указано, что несколько букв остались без кодовых слов (как, например, в задании демоварианта), то кодовое слово для указанной буквы должно быть подобрано таким образом, чтобы осталась возможность найти кодовые слова, удовлетворяющие условию Фано, и для других букв. Так, например, если мы букву А закодируем нулём, а букву Б единицей, то букву В мы уже никак не сможем закодировать с соблюдением условия Фано, поэтому длину кодового слова для А или Б следует увеличить»
ФГБНУ «Федеральный институт педагогических измерений»
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- Кодирование бывает равномерным и неравномерным:
- при равномерном кодировании всем символам соответствуют коды одинаковой длины;
- при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
- если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
- условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Однозначное декодирование обеспечивается:
Однозначное декодирование
Декодирование
Егифка ©:
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
ЕГЭ 4.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
✍ Решение:
- Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
ВОДОПАД:010010001110010
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Теоретическое решение ЕГЭ данного задания по информатике, видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Рассмотрим еще разбор 4 задания ЕГЭ:
ЕГЭ 4.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
✍ Решение:
- Во-первых, проверяем условие Фано: никакое кодовое слово не является началом другого кодового слова. Условие верно.
- Код разбиваем слева направо согласно данным, представленным в таблице. Затем переведём его в буквы:
✎ 1 вариант решения:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
✎ 2 вариант решения:
-
Этот вариант решения 4 задания ЕГЭ более сложен, но тоже верен.
- Сделаем дерево, согласно кодам в таблице:
- Сопоставим закодированное сообщение с кодами в дереве:
110 000 01 001 10
Результат: b a c d e.
Кроме того, вы можете посмотреть видеорешение этого задания ЕГЭ по информатике (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Решим следующее 4 задание:
ЕГЭ 4.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).
Определите, какое число передавалось по каналу в виде 01100010100100100110.
✍ Решение:
- Рассмотрим пример из условия задачи:
Было2310 Стало00101001102
0010100110 (0010 - 2, 0011 - 3)
01100 01010 01001 00110
0110 0101 0100 0011
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видеорешение этого задания ЕГЭ по информатике, теоретическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
ЕГЭ 4.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Подобные задания для тренировки
✍ Решение:
✎
1 вариант решения
основан на логических умозаключениях:
- Найдём самые короткие возможные кодовые слова для всех букв.
- Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
- Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
- Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
- Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
- Будем использовать дерево. Влево откладываем 0, вправо — 1:
- Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
4.5:
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:
А: 101010, Б: 011011, В: 01000
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
- Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
4.6:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:
А - 01 Б - 00 В - 11 Г - 100
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
- Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
- Перепишем сверху вниз получившееся кодовое слово для Д: 101
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
4.7: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100
Подробное теоретическое решение данного 4 (раньше №5) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
4.8:
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
- Получившееся числовое значение кодового слова для буквы Г — 01.
- Получившееся числовое значение кодового слова для буквы Г — 00.
- После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Дерево по условию Фано (однозначно декодируется с начала):
Дерево по обратному условию Фано (однозначно декодируется с конца):
Результат: 00
4.9:
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
Подобные задания для тренировки
✍ Решение:
- С помощью дерева отобразим известные коды для букв:
- В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
- Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Результат: 20
Смотрите виде решения задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Содержание
- Информатика ЕГЭ 4 задание разбор, кодирование и декодирование информации
- Как найти длину кодового слова
- Как найти длину кодового слова
- РАЗБОР ЗАДАНИЯ 5 ЕГЭ ПО ИНФОРМАТИКЕ 2017
- Как найти длину кодового слова
Информатика ЕГЭ 4 задание разбор, кодирование и декодирование информации
4-е задание: «Кодирование и декодирование информации»
Уровень сложности — базовый,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 2 минуты.
Проверяемые элементы содержания: Умение кодировать и декодировать информацию
Плейлист видеоразборов задания на YouTube:
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
Ответ: 22162
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Ответ: b a c d e
Результат: b a c d e.
- Этот вариант решения 4 задания ЕГЭ более сложен, но тоже верен.
Ответ: 6 5 4 3
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Ответ: 9
Ответ: 00
Ответ: 101
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Ответ: 1100

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Ответ: 00
Дерево по условию Фано (однозначно декодируется с начала):
Дерево по обратному условию Фано (однозначно декодируется с конца):
Результат: 00
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
Ответ: 20
Источник
Как найти длину кодового слова
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Найдём наиболее короткие представления для всех букв. Кодовые слова 01 и 00 использовать нельзя, поскольку тогда нарушается условие Фано. Используем, например, для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано. Следовательно, для оставшихся двух букв нужно использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Тогда суммарная длина всех четырёх кодовых слов равна
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 1; Б — 0100; В — 000; Г — 011; Д — 0101. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
Для однозначного декодирования получившееся в результате сокращения кодовое слово не должно быть началом никакого другого. Первый вариант ответа не подходит, поскольку код буквы А является началом кода буквы Г. Второй вариант ответа подходит. Третий вариант ответа не подходит, т. к. в таком случае код буквы Г является началом кода буквы Д.
Правильный ответ указан под номером: 2.
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К – кодовое слово 10. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Нельзя использовать кодовые слова, которые начинаются с 0 или с 10. 11 также не можем использовать, поскольку тогда мы больше не сможем взять никакое другое кодовое слово, а нам их нужно пять. Поэтому берём трёхзначное 110. 111 опять же не можем использовать, потому что понадобиться ещё одно кодовое слово, а вместе с этим не останется больше свободных. Теперь осталось взять всего два слова и это будут 1110 и 1111. Итого имеем 0, 10, 110, 1110 и 1111 — 14 символов.
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М – кодовое слово 01. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Условие Фано — никакое кодовое слово не может быть началом другого кодового слова. Так как уже имеется кодовое слово 1, то никакое другое не может начинаться с 1. Только с 0. Также не может начинаться с 01, поскольку у нас уже есть 01. То есть любое новое кодовое слово будет начинаться с 00. Но это не может быть 00, так как иначе мы не сможем взять больше ни одного кодового слова, поскольку все более длинные слова начинаются либо с 1, либо с 00, либо с 01. Мы можем взять либо 000, либо 001. Но не оба сразу, поскольку опять же в таком случае мы больше не сможем взять ни одного нового кода. Тогда возьмём 001. И так как нам осталось всего два кода, то можем взять 0000 и 0001. Итого имеем: 1, 01, 001, 0000, 0001. Всего 14 символов.
Источник
Как найти длину кодового слова
010 010 001 110 010
Результат: 22162
Решение ЕГЭ данного задания по информатике, видео:
ЕГЭ 5.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
| 000 | 110 | 01 | 001 | 10 |
Результат: b a c d e.
2 вариант решения: Этот вариант решения 5 задания ЕГЭ более сложен, но тоже верен.
Результат: b a c d e.
Кроме того, вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
Решим следующее 5 задание:
Где сами цифры исходного числа: 0010 1 0011 0 (0010 — 2, 0011 — 3)
Первая добавленная цифра 1 после двоичной двойки — это проверка четности (1 единица в 0010 — значит нечетное), 0 после двоичной тройки — это также проверка нечетности (2 единицы в 0011, значит — четное).
Исходя из разбора примера решаем нашу задачу так: поскольку «нужные» нам цифры образуются из групп по 4 числа в каждой плюс одно число на проверку четности, то разобьем закодированное сообщение на группы по 5, и отбросим из каждой группы последний символ:
01100 01010 01001 00110
0110 0101 0100 0011
Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
Значит для надо использовать трёхзначные кодовые слова. Закодируем буквы Л и Мкодовыми словами 110 и 111.
Суммарная длина всех четырёх кодовых слов равна (Н)1 + (К)2 + (Л)3 + (М)3 = 9.
1 вариант решения: будем использовать дерево
Суммарная длина всех четырёх кодовых слов равна (Н)1 + (К)2 + (Л)3 + (М)3 = 9.
РАЗБОР ЗАДАНИЯ 5 ЕГЭ ПО ИНФОРМАТИКЕ 2017
Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
1 — не подходит (все буквы кроме А начинаются с 1)
10 — не подходит (соответствует коду Д)
11 — не подходит (начало кодов Б, В и Г)
100 — не подходит (код Д — 10 — является началом данного кода)
101 — не подходит (код Д — 10 — является началом данного кода)
110 — не подходит (начало кода В и Г)
111 — не подходит (соответствует коду Б)
1000 — не подходит (код Д — 10 — является началом данного кода)
1001 — не подходит (код Д — 10 — является началом данного кода)
1010 — не подходит (код Д — 10 — является началом данного кода)
1011 — не подходит (код Д — 10 — является началом данного кода)
1100 — не подходит (начало кода В и Г)
1101 — подходит
Результат: 1101
Более подробное решение данного задания представлено в видеоуроке:
Источник
Как найти длину кодового слова
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А – 11, B – 101, C – 0. Какова наименьшая возможная суммарная длина всех кодовых слов?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Заметим, что для алфавита из трёх букв, код с наименьшей суммарной длиной кодовых слов, удовлетворяющий условию Фано имел бы длину 1 + 2 + 2 = 5. Для алфавита из четырёх букв: 1 + 2 + 3 + 3 = 9. Аналогично можно получить минимальную длину суммарную длину кодовых слов для алфавита, содержащего произвольное число символов.
Удостоверимся, что, используя кодовые слова, приведённые в условии можно построить код, удовлетворяющий условию Фано и имеющий наименьшую суммарную длину. Будем использовать для буквы D кодовое слово 1000, для буквы E кодовое слово 10010, для буквы F 10011.
Суммарная длина такого кода 1 + 2 + 3 + 4 + 5 + 5 = 20.
По каналу связи передаются сообщения, содержащие только четыре буквы: З, А, Р, Я; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв Я, Р, З используются такие кодовые слова: Я — 0, Р — 101; З — 110.
Укажите кратчайшее кодовое слово для буквы А, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наибольшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Заметим, что кодовое слово не может начинаться с нуля, поскольку будет нарушено условие Фано. Кодовые слова 10 и 11 взять нельзя, поскольку будет нарушено условие Фано. Можно взять кодовые слова длины 3: 100 и 111. Поскольку числовое значение кодового слова 100 меньше, возьмём кодовое слово 111.
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Найдём наиболее короткие представления для всех букв. Кодовые слова 01 и 00 использовать нельзя, поскольку тогда нарушается условие Фано. Используем, например, для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано. Следовательно, для оставшихся двух букв нужно использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Тогда суммарная длина всех четырёх кодовых слов равна
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М — кодовое слово 01. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Найдём для оставшихся двух символов наиболее короткое представление, удовлетворяющее условию Фано. Кодовое слово 0 использовать нельзя, так как тогда нарушится условие Фано. Из двузначных кодовых слов можно использовать слово 00, а слова 10 и 11 использовать нельзя. При таком построении кодов для четвёртого символа невозможно подобрать кодовое слово.
Поэтому 00 использовать не будем, а будем использовать трёхзначные кодовые слова, например, 000 и 001. Тогда суммарная длина всех четырёх кодовых слов равна 1 + 2 + 3 + 3 = 9.
Аналоги к заданию № 7658: 7685 Все
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Найдём для оставшихся двух символов наиболее короткое представление, удовлетворяющее условию Фано. Кодовое слово 1 использовать нельзя, так как тогда нарушится условие Фано. Из двузначных кодовых слов можно использовать слово 10, а слова 11 и 01 использовать нельзя. При таком построении кодов для четвёртого символа невозможно подобрать двухзначное кодовое слово. Поэтому используем трёхзначное слово, а именно — 111.
Таким образом, наименьшая возможная суммарная длина всех четырёх кодовых слов будет 1 + 3 + 2 + 3 = 9.
Правильный ответ указан под номером 3.
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М — кодовое слово 011. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Найдём для оставшихся двух символов наиболее короткое представление, удовлетворяющее условию Фано. Кодовое слово 0 использовать нельзя, так как тогда нарушится условие Фано. Из двузначных кодовых слов можно использовать слово 00, а слова 11 и 01 использовать нельзя. При таком построении кодов для четвёртого символа невозможно подобрать двухзначное кодовое слово. Поэтому используем трёхзначное слово, а именно 010.
Таким образом, наименьшая возможная суммарная длина всех четырёх кодовых слов будет 1 + 3 + 2 + 3 = 9.
Правильный ответ указан под номером 2.
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В используются такие кодовые слова: А — 0;
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для того, чтобы сообщение, записанное с помощью неравномерного по длине кода, однозначно раскодировалось, требуется, чтобы никакой код не был началом другого (более длинного) кода.
Рассмотрим варианты для буквы Г, начиная с самого короткого.
1) Г=1: код буквы Г является началом кода буквы Б — 110, поэтому этот вариант не подходит.
2) Если код Г=01, то условие Фано нарушается, поскольку тогда код буквы А является началом кода буквы Г.
3) Если код Г=101, то условие Фано не нарушается. Данное кодовое слово является кратчайшим для буквы Г.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А – 00, B – 010, C – 1. Какова наименьшая возможная суммарная длина всех кодовых слов?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Для нахождения кодовых слов будем использовать двоичное дерево, в котором от каждого узла отходит две ветви, соответствующие выбору следующей цифры кода. Буквы будем размещать на конечных узлах дерева — листьях. Условие Фано выполняется, поскольку при проходе от корня дерева к букве в середине пути не встречается других букв.
Пример дерева, обеспечивающего минимальную сумму длин всех шести кодов изображено на рисунке.
Суммарная длина такого кода 1 + 2 + 3 + 4 + 5 + 5 = 20.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Однозначные коды не подходят по условию Фано. Кратчайшее подходящее кодовое слово — 01. Но выбирая его, не останется вариантов закодировать букву E, значит, нужно взять минимум трехзначный код. Минимальный из них, подходящий по условию Фано — 010. Тогда букву Е можно закодировать как 011.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Поскольку все однозначные и двузначные слова не подходят по условию Фано, нужно найти трехзначное слово, которое было бы максимально и удовлетряло условию. Так как 111, 101 и 110 нарушают условие Фано, то искомое слово — 010.
Заметим, что двузначное кодовое слово 01 не подходит, поскольку при его использовании нельзя подобрать кодовое слово для буквы Е.
Дублирует задание 13481.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу. Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Поскольку все однозначные и двузначные слова не подходят по условию Фано, значит, нужно найти трехзначное слово, которое было бы минимально и удовлетворяло условию. Это слово — 100. Однако при выборе кода 100 мы закрываем возможные варианты для D И E. Значит, трехзначные слова нам тоже не подходят, если взять четырехзначные то там мы для кодирования можем взять слово 1000. Тогда для кодирования D и E можно использовать слова 10010 и 10011.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0.
Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наибольшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
Имеющиеся кодовые слова имеют длину один, два и три, следовательно, наименьшая длина кодового слова для буквы F равна четырём. Кодовое слово, удовлетворяющее условию Фано — 1001.
Заметим, что более короткое кодовое слово 100 не подходит, поскольку тогда невозможно найти кодовые слова для букв D и E.
Код 1000 не подходит, так как сказано «Если таких слов несколько, укажите то из них, которое соответствует наибольшему возможному двоичному числу».
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, М, Р, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 010, Б — 00, Г — 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Следующая буква должна кодироваться как 011, поскольку 01 мы взять не можем, иначе код для буквы А не будет удовлетворять условию Фано. 10 из-за Г взять не можем, тогда следующая буква будет кодироваться как 100. Следующая буква должна кодироваться как 110, поскольку 11 взять не можем, иначе не останется кодовых слов для оставшейся буквы, которые удовлетворяют условию Фано. Значит, последняя буква будет кодироваться как 111. Тогда наименьшее количество двоичных знаков, которые потребуются для кодирования слова МАГИЯ равно
Заметим, что после кодирования всех букв, входящих в слово МАГИЯ, должен остаться хотя бы один свободный код для кодирования буквы Р, которая не входит в данное слово, но может передаваться по каналу связи. Проверить наличие свободного кода можно, построив дерево кодов, как показано в задаче 18553.
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 0, Б — 1011. Укажите сумму длин кратчайших кодовых слов для букв В и Г, которые будут удовлетворять условию Фано.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Для двух букв кодовые слова уже известны, осталось подобрать для оставшихся двух букв такие кодовые слова, которые будут являться кратчайшими и удовлетворять условию Фано.
Кодовые слова не могут начинаться с 0, поскольку 0 является кодовым словом для буквы А. Кодовым словом для буквы В будет являться 11. Кодовым словом для буквы Г будет являться 100, кодовое слово 101 взять не можем, поскольку кодовым словом для буквы Б является 1011.
Таким образом, сумма длин кратчайших кодовых слов для букв В и Г будет равна 2 + 3 = 5.
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв К, Л, М, Н использовали соответственно кодовые слова 000, 001, 010, 11. Для двух оставшихся букв — П и Р — длины кодовых слов неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для четырёх букв кодовые слова уже известны, осталось подобрать для оставшихся двух букв такие кодовые слова, которые будут являться кратчайшими и удовлетворять условию Фано.
Кодовым словом не могут быть ни 0, ни 1, потому что есть кодовые слова, начинающиеся с 0 и 1. Для оставшихся букв можно использовать кодовые слова 10 и 011. Кратчайшее слово — 10.
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Л использовали кодовое слово 1, для буквы М – кодовое слово 01. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Условие Фано — никакое кодовое слово не может быть началом другого кодового слова. Так как уже имеется кодовое слово 1, то никакое другое не может начинаться с 1. Только с 0. Также не может начинаться с 01, поскольку у нас уже есть 01. То есть любое новое кодовое слово будет начинаться с 00. Но это не может быть 00, так как иначе мы не сможем взять больше ни одного кодового слова, поскольку все более длинные слова начинаются либо с 1, либо с 00, либо с 01. Мы можем взять либо 000, либо 001. Но не оба сразу, поскольку опять же в таком случае мы больше не сможем взять ни одного нового кода. Тогда возьмём 001. И так как нам осталось всего два кода, то можем взять 0000 и 0001. Итого имеем: 1, 01, 001, 0000, 0001. Всего 14 символов.
Источник
Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.
Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.
Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.
Задача 1
Для кодирования букв О, В, Д, П, А решили использовать двоичное представление
чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится
1) 22162
2) 1020342
3) 2131453
4) 34017
Решение:
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для одноразрядных чисел:
| О | В | Д | П | А |
| 0 | 1 | 2 | 3 | 4 |
| 00 | 01 | 10 | 11 | 100 |
Закодируем последовательность букв: ВОДОПАД — 010010001110010.
Разобьём это представление на тройки справа налево и переведём каждую тройку в восьмеричное число.
010 010 001 110 010 — 22162.
Правильный ответ указан под номером 1.
Ответ: 1
Задача 2
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
1) D3A6
2) 62032206
3) 6A3D
4) CADBAADC
Решение:
Закодируем последовательность букв: ВАГБААГВ — 1101001110100110. Разобьем это представление на четвёрки справа налево и переведём каждую четверку в шестнадцатеричное число:
1101 0011 1010 01102 = D3A616
Правильный ответ указан под номером 1.
Ответ: 1
Задача 3
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
| 100 | 110 | 011 | 01 | 10 |
Определите, какой набор букв закодирован двоичной строкой 1000110110110, если известно, что все буквы в последовательности – разные:
1) cbade
2) acdeb
3) acbed
4) bacde
Решение:
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит код можно раскодировать неоднозначно.
Значит, будем перебирать варианты, пока не получим подходящее слово :
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.
Такой вариант удовлетворяет условию, значит, окончательно получили ответ: acdeb.
Ответ: 2
Задача 4
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110). Определите, какое число передавалось по каналу в виде 01010100100111100011?
1) 59143 2) 5971 3) 102153 4) 10273
Решение:
При кодировании под саму цифру отводится 4 разряда, и еще один под код проверки четности (т.е. всего под цифру отводится 5 разрядов).
Разобьем заданную последовательность на группы по 5 бит в каждой:
01010, 10010, 01111, 00011.
отбросим пятый (последний) бит в каждой группе:
0101, 1001, 0111, 0001.
это и есть двоичные коды передаваемых чисел:
01012 = 5, 10012 = 9, 01112 = 7, 00012 = 1.
таким образом, были переданы числа 5, 9, 7, 1 или число 5971.
Ответ: 2
Задача 5
По каналу связи передаются сообщения, содержащие только 4 буквы — П, О, Р, Т. Для кодирования букв используются 5-битовые кодовые слова:
П — 11111, О — 11000, Р — 00100, Т — 00011.
Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях.
Это свойство важно для расшифровки сообщений при наличии помех (в предположении, что передаваемые биты могут искажаться, но не пропадают). Закодированное сообщение считается принятым корректно, если его длина кратна 5 и каждая пятёрка отличается от некоторого кодового слова не более чем в одной позиции; при этом считается, что пятёрка кодирует соответствующую букву. Например, если принята пятерка 00000, то считается, что передавалась буква Р.
Среди приведённых ниже сообщений найдите то, которое принято корректно, и укажите его расшифровку (пробелы несущественны).
11011 11100 00011 11000 01110
00111 11100 11110 11000 00000
1) ПОТОП
2) РОТОР
3) ТОПОР
4) ни одно из сообщений не принято корректно
Решение:
Длина обоих сообщений кратна пяти.
Анализируя первое сообщение «11011 11100 00011 11000 01110», приходим к выводу, что оно принято некорректно, поскольку нет такого слова, которое бы отличалось от слова «01110» только в одной позиции.
Рассмотрим второе сообщение. Учитывая, что каждая пятёрка отличается от некоторого кодового слова не более чем в одной позиции, его возможно расшифровать только как «ТОПОР».
Ответ: 3
Задача 6
Для передачи данных по каналу связи используется 5-битовый код. Сообщение содержит только буквы А, Б и В, которые кодируются следующими кодовыми словами: А — 11010, Б — 10111, В — 01101.
При передаче возможны помехи. Однако некоторые ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов отличаются друг от друга не менее чем в трёх позициях. Поэтому если при передаче слова произошла ошибка не более чем в одной позиции, то можно сделать обоснованное предположение о том, какая буква передавалась. (Говорят, что «код исправляет одну ошибку».) Например, если получено кодовое слово 10110, считается, что передавалась буква Б. (Отличие от кодового слова для Б только в одной позиции, для остальных кодовых слов отличий больше.) Если принятое кодовое слово отличается от кодовых слов для букв А, Б, В более чем в одной позиции, то считается, что произошла ошибка (она обозначается ‘х’).
Получено сообщение 11000 11101 10001 11111. Декодируйте это сообщение — выберите правильный вариант.
1) АххБ
2) АВхБ
3) хххх
4) АВББ
Решение:
Декодируем каждое слово сообщения. Первое слово: 11000 отличается от буквы А только одной позицией. Второе слово: 11101 отличается от буквы В только одной позицией. Третье слово: 10001 отличается от любой буквы более чем одной позицией. Четвёртое слово: 11111 отличается от буквы Б только одной позицией.
Таким образом, ответ: АВхБ.
Ответ: 2
Однозначное декодирование. Условие Фано
Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.
Равномерное кодирование всегда однозначно декодируемо.
Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:
Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.
Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.
Задача 7
Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 0001
2) 000
3) 11
4) 101
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.
Ответ: 2
Задача 8
Для кодирования некоторой последовательности, состоящей из букв У, Ч, Е, Н, И и К, используется неравномерный двоичный префиксный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему остался префиксным? Коды остальных букв меняться не должны.
Выберите правильный вариант ответа.
Примечание. Префиксный код — это код, в котором ни одно кодовое слово не является началом другого; такие коды позволяют однозначно декодировать полученную двоичную последовательность.
1) кодовое слово для буквы Е можно сократить до 01
2) кодовое слово для буквы К можно сократить до 1
3) кодовое слово для буквы Н можно сократить до 10
4) это невозможно
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Легко заметить, что если букву Н перенести в вершину 10, она останется листом. Т.е. кодовое слово для буквы Н можно сократить до 10.
Правильный ответ указан под номером 3.
Ответ: 3
Задача 9
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
1) 7
2) 8
3) 9
4) 10
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Легко заметить, что ближайшие от корня свободные листы (т.е. свободные коды с наименьшей длиной) – это 10 и 111. Таким образом, наименьшая возможная суммарная длина всех четырёх кодовых слов будет 1 + 3 + 2 + 3 = 9.
Правильный ответ указан под номером 3.
Ответ: 3
Задача 10
По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Легко заметить, что ближайшие от корня свободные листы (т.е. свободные коды с наименьшей длиной) – это 101 и 110. Наименьшее числовое значение имеет код 101.
Ответ: 101
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «6. Задание 4. Кодирование и декодирование информации» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
189
Добавлен:
17.03.2016
Размер:
349.7 Кб
Скачать
© К.
Поляков, 2009-2016
Тема: Кодирование и декодирование
информации.
Что нужно знать:
-
кодирование
– это перевод информации с одного языка
на другой (запись в другой системе
символов, в другом алфавите) -
обычно
кодированием называют перевод информации
с «человеческого» языка на формальный,
например, в двоичный код, а декодированием
– обратный переход -
один
символ исходного сообщения может
заменяться одним символом нового кода
или несколькими символами, а может быть
и наоборот – несколько символов
исходного сообщения заменяются одним
символом в новом коде (китайские
иероглифы обозначают целые слова и
понятия) -
кодирование
может быть равномерноеинеравномерное;
при равномерном
кодировании все символы кодируются
кодами равной длины;
при неравномерном
кодировании разные символы могут
кодироваться кодами разной длины, это
затрудняет декодирование -
закодированное
сообщение можно однозначно декодировать
с начала, если выполняется условие
Фано: никакое кодовое слово не является
началом другого кодового слова; -
закодированное
сообщение можно однозначно декодировать
с конца, если выполняется обратное
условие Фано: никакое кодовое слово
не является окончанием другого кодового
слова; -
условие
Фано – это достаточное, но не необходимое
условие однозначного декодирования.
Ещё пример задания
Р-13. По каналу связи передаются
сообщения, каждое из которых содержит
16 букв А, 8 букв Б, 4 буквы В и 4 буквы Г
(других букв в сообщениях нет). Каждую
букву кодируют двоичной последовательностью.
При выборе кода учитывались два
требования:
а) ни одно кодовое слово не является
началом другого (это нужно, чтобы код
допускал однозначное декодирование);
б) общая длина закодированного
сообщения должна быть как можно меньше.
Какой код из приведённых ниже следует
выбрать для кодирования букв А, Б, В и
Г?
1) А:0, Б:10, В:110, Г:111
2) А:0, Б:10, В:01, Г:11
3) А:1, Б:01, В:011, Г:001
4) А:00, Б:01, В:10, Г:11
Решение:
-
сначала выберем коды, в которых ни одно
кодовое слово не совпадет с началом
другого (такие коды называю префиксными) -
для кода 2 условие «а» не выполняется,
так как кодовое слово буквы В (01)
начинается с кодового слова буквы А
(0) -
для кода 3 условие «а» не выполняется,
так как кодовое слово буквы В (011)
начинается с кодового слова буквы Б
(01) -
для кодов 1 и 4 условие выполняется, их
рассматриваем дальше -
считаем общее количество битов в
сообщении для кода 1:
16∙1 + 8·2 + 4∙3 + 4∙3 = 56 битов
-
считаем общее количество битов в
сообщении для кода 4:
16∙2 + 8·2 + 4∙2 + 4∙2 = 64
бита
-
код 1 даёт наименьшую длину сообщения,
поэтому выбираем его -
Ответ: 1.
Ещё пример задания
Р-12. Для кодирования некоторой
последовательности, состоящей из букв
А, Б, В, Г, решили использовать неравномерный
двоичный код, удовлетворяющий условию
Фано. Для буквы А использовали кодовое
слово 0, для буквы Б – кодовое слово 110.
Какова наименьшая возможная суммарная
длина всех четырёх кодовых слов?
1)
7 2) 8 3) 9 4) 10
Решение (способ 1, исключение вариантов):
-
условие
Фано означает, что ни одно кодовое слово
не совпадает с началом другого кодового
слова -
поскольку
уже есть кодовое слово 0, ни одно другое
кодовое слово не может начинаться с 0 -
поскольку
есть код 110, запрещены кодовые слова 1,
11; кроме того, ни одно другое кодовое
слово не может начинаться с 110 -
таким
образом, нужно выбрать еще два кодовых
слова, для которых выполняются эти
ограничения -
есть
одно допустимое кодовое слово из двух
символов: 10 -
если
выбрать кодовое слово 10 для буквы В, то
остаётся одно допустимое трёхсимвольное
кодовое слово – 111, которое можно выбрать
для буквы Г -
таким
образом, выбрав кодовые слова А – 0, Б
– 110, В – 10, Г – 111, получаем суммарную
длину кодовых слов 9 символов -
если
же не выбрать В – 10, то есть три допустимых
трёхсимвольных кодовых слова: 100, 101 и
110; при выборе любых двух их них для букв
В и Г получаем суммарную длину кодовых
слов 10, что больше 9; поэтому выбираем
вариант 3 (9 символов) -
Ответ:
3.
Решение (способ 2, построение дерева):
-
условие
Фано означает, что ни одно кодовое слово
не совпадает с началом другого кодового
слова; при этом в дереве кода все кодовые
слова должны располагаться в листьях
дерева, то есть в узлах, которые не имеют
потомков; -
построим
дерево для заданных кодовых слов А –
0 и Б – 110:
-
штриховыми
линиями отмечены две «пустые» ветви,
на которые можно «прикрепить» листья
для кодовых слов букв В (10) и Г (111)
-
таким
образом, выбрав кодовые слова А – 0, Б
– 110, В – 10, Г – 111, получаем суммарную
длину кодовых слов 9 символов -
Ответ:
3.
Соседние файлы в папке ЕГЭ 2016-11 класс
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #