|
0 |
Задачу можно решить куда легче, если вы введете декартову систему координат, наложите ее на трапецию, приняв за начало координат точку, являющуюся серединой основания трапеции. Далее вы нехитрым способом вычислите координаты всех необходимые точек( с помощью теоремы Пифагора ) и составите уравнения прямых, на которых лежат стороны трапеции. ссылка
отвечен 0xFFh изменен
|
Ответ:
1)
ОС= 12 , AB = 1/2 OC , значит AB = 6
Введем систему координат точка О начальная точка, тогда её координаты {0;0},
А {0;8} по условию
С {12;0}
В {6;8}
Тогда BC=sqrt((12-6)²+(8-0)²)= 10
Тогда OB=sqrt((6-0)²+(8-0)²)= 10
2)
1) Находим длины отрезков AB, AC,BD,DC по координатам
2) Воспользуемся свойством биссектрисы:
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
см. рис. в приложении подробное решение подобной задачи

|
1 / 1 / 0 Регистрация: 12.12.2014 Сообщений: 61 |
|
|
1 |
|
Написать уравнение сторон равнобедренной трапеции14.01.2015, 18:25. Показов 10058. Ответов 6
Условие: Кликните здесь для просмотра всего текста
Написать уравнение сторон равнобедренной трапеции, зная середины ее оснований (1;1), (2;8) и точки Из этой задачи я смог найти уравнение оснований, зная что нормальный вектор перпендикулярен этим основаниям. А вот как найти уравнения боковых сторон?
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
15.01.2015, 07:07 |
2 |
|
Проще всего так.
0 |
|
1 / 1 / 0 Регистрация: 12.12.2014 Сообщений: 61 |
|
|
15.01.2015, 09:08 [ТС] |
3 |
|
Идея понятна, но непонятно одно — как вот например вы получили симметричную точку (-3,-2)? Как расчитать её координаты?
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
15.01.2015, 09:45 |
4 |
|
Как расчитать её координаты? Пусть A — заданная точка, B — симметричная ей относительно прямой L. Тогда вектор AB ортогонален L (первое уравнение), середина отрезка АВ лежит на L (второе уравнение).
0 |
|
1 / 1 / 0 Регистрация: 12.12.2014 Сообщений: 61 |
|
|
15.01.2015, 10:12 [ТС] |
5 |
|
Ну ,они оротогональны (AB и L), и как мне из этого получить координаты симметричной точки (-3,-2)?
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,063 |
|
|
15.01.2015, 14:27 |
6 |
|
Ну ,они оротогональны (AB и L), и как мне из этого получить координаты симметричной точки (-3,-2)? Да, уж. Пусть А(4,-3), В(х,у). Тогда АВ=(х-4,у+3). Так как AB и L ортогональны и (1,7) — направляющий вектор L, то Далее, координаты середины М отрезка АВ равны полусумме координат его концов; отсюда М((х+4)/2,(у-3)/2). Так как М лежит на прямой L, то Решайте систему для вычисления координат точки В.
0 |
|
6354 / 4062 / 1510 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
15.01.2015, 14:41 |
7 |
|
Ну ,они оротогональны (AB и L), и как мне из этого получить координаты симметричной точки (-3,-2)? Можно привести формулу в общем виде. Если уравнение прямой задано в общем виде (через нормальный вектор) Добавлено через 13 минут
0 |
Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.
- Длина основания через среднию линию и другое известное
основание - Нижнее основание через верхнее основание, высоту и углы при
нижнем основании - Верхнее основание через нижнее основание, высоту и углы при
нижнем основании - Нижнее основание через боковые стороны, верхнее основание и
углы при нижнем основании - Верхнее основание через боковые стороны, нижнее основание и
углы при нижнем основании - Боковую сторону через высоту и угол при нижнем
основании
Длина основания через среднюю линию и известное основание
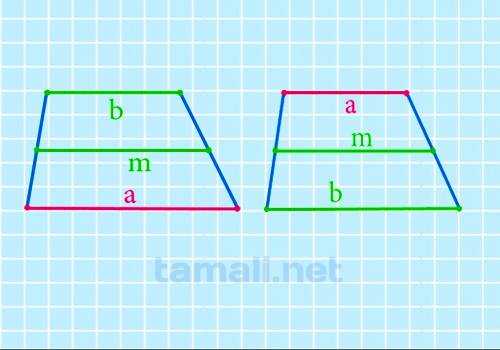
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Цифр после
запятой:
Результат в:
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
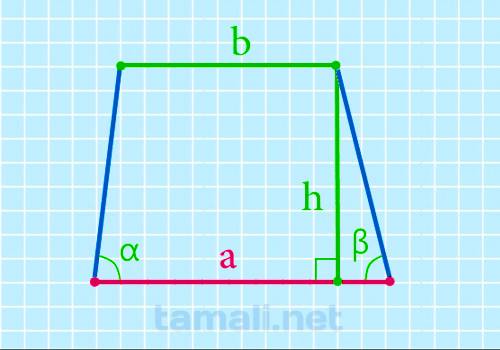
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Цифр после
запятой:
Результат в:
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
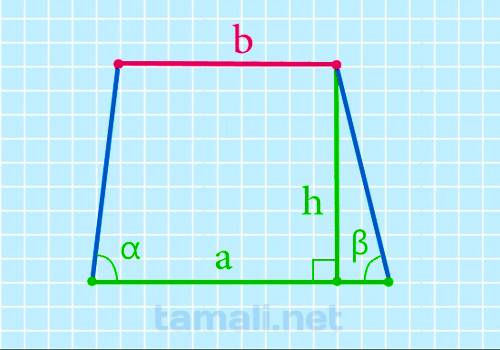
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:
b = a – h*(ctg α + ctg β)
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
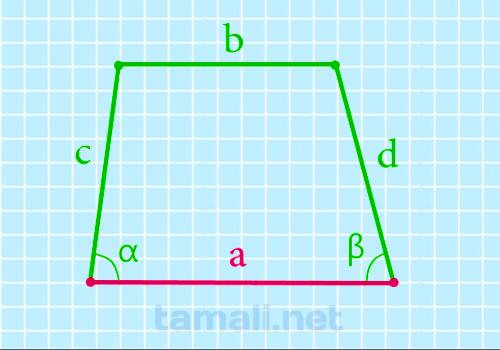
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них
a = b + c * cos α + d * cos β
Цифр после
запятой:
Результат в:
Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82
Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
= (144 – 64)/4 = 20 - В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
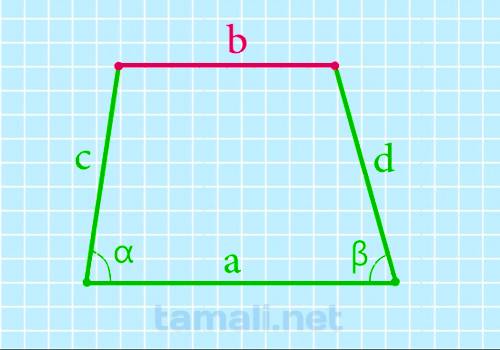
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них
b = a – c * cos α – d * cos β
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
11*11)/12= (169 – 121)/12 = 4 - Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
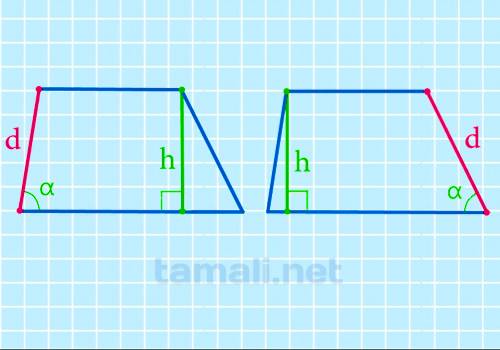
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Цифр после
запятой:
Результат в:
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)
- В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
22*2/2 = 112 - Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
градусам. Найти MP: MP = (32 – 19)*3 = 133 - В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269
Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.
Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.
- В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
13)/3/2 = 103 - В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
90 - В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
(36 – 17)^2) = 841 – 361= 480 = 430
Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.
- В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
100 – 96 = 4 - Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2 - В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2 - Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
треугольник. - Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
градусов.
Свойства трапеции
- Средняя линия параллельна основаниям и равна их полусумме.
- Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
отрезок с длиной боковой стороны. - Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
Коэффициент
подобия – k = AD/BC.
Отношение площадей треугольников — k^2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
площадь. - В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
боковых сторон лежат на одной прямой. - Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
линии.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Как написать уравнение сторон равнобедренной трапеции
|
|||
|
Нужна помощь по аналитической геометрии Как на писать уравнение сторон равнобедренной трапеции, зная середины ее оснований (-1,1) и (1,3) точки на ее боковых сторонах (3,0),(-3,5)?
|
||
| Вернуться к началу |
|
||
|
Zdrastes |
Заголовок сообщения: Re: Как на писать уравнение сторон равнобедренной трапеции
|
|
mad_math писал(а): Вектор, соединяющий середины оснований будет им перпендикулярен. Находите координаты этого вектора и составляете уравнения оснований, как уравнение прямой, проходящей через точку (середина основания) перпендикулярно вектору, соединяющему середины оснований. уравнения оснований составила,не могу найти координаты вектора,соединяющего основания,а следовательно и уравнения боковых сторон,можно поподробнее об этом?
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Как написать уравнение сторон равнобедренной трапеции
|
|
А я-то надеялась, что есть какой-то хитрый ход без использования оси симметрии. Zdrastes писал(а): уравнения оснований составила И что получилось?
|
|
| Вернуться к началу |
|
|
Zdrastes |
Заголовок сообщения: Re: Как написать уравнение сторон равнобедренной трапеции
|
|
mad_math писал(а): А я-то надеялась, что есть какой-то хитрый ход без использования оси симметрии. Zdrastes писал(а): уравнения оснований составила И что получилось? y=-x и y=-x-4,но на самом деле,я уже совсем запуталась и не понимаю что делаю,скорее всего это неверно
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Угол наклона боковых сторон равнобедренной трапеции
в форуме Начала анализа и Другие разделы школьной математики |
neverlucky |
5 |
241 |
09 янв 2020, 04:48 |
|
Как записать уравнение боковых сторон прямоугольной трапеции
в форуме Аналитическая геометрия и Векторная алгебра |
Root |
1 |
475 |
15 дек 2013, 16:17 |
|
Угол между диогоналями в равнобедренной трапеции
в форуме Геометрия |
leonidzilb |
4 |
418 |
29 апр 2015, 22:58 |
|
Найти боковую сторону равнобедренной трапеции
в форуме Геометрия |
wehrwolf |
2 |
478 |
08 апр 2014, 16:44 |
|
Найти длину боковой стороны равнобедренной трапеции
в форуме Геометрия |
ncux01 |
1 |
373 |
21 дек 2017, 12:12 |
|
Даны координаты сторон треугольника, написать уравнение и
в форуме Аналитическая геометрия и Векторная алгебра |
kity2503 |
4 |
572 |
01 май 2016, 21:16 |
|
Написать уравнение сторон треугольника, медианы, высоты и
в форуме Геометрия |
kity2503 |
1 |
752 |
01 май 2016, 21:14 |
|
Построение равнобедренной трапеции — задача на построение
в форуме Геометрия |
maksim03 |
15 |
618 |
29 апр 2022, 10:25 |
|
Написать уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Neyrys |
1 |
324 |
03 дек 2016, 04:59 |
|
Написать уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Iris94 |
5 |
574 |
29 ноя 2018, 08:57 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 13 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |






