6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Правильный шестиугольник (страница 2)
Правильный шестиугольник — выпуклый шестиугольник, у которого все углы равны и все стороны равны.
(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).
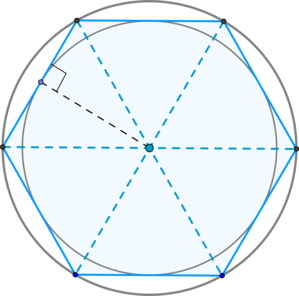
(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]
Задание
8
#667
Уровень задания: Равен ЕГЭ
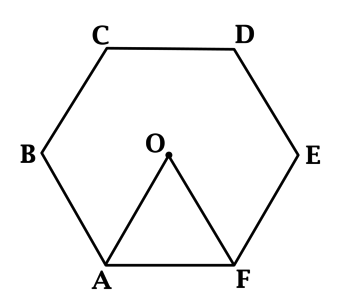
Сторона правильного шестиугольника (ABCDEF) равна (sqrt[4]{3}). Найдите его площадь.
Пусть (O) – центр описанной около (ABCDEF) окружности
тогда треугольники (AOF), (AOB), (BOC), (COD), (DOE), (EOF) – равносторонние и все они попарно равны.
[S_{triangle{AOF}} = 0,5 AF^2 cdot sin{60^{circ}} = dfrac{AF^2sqrt{3}}{4}, qquadqquad S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2}.] В данной задаче (S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2} = 4,5).
Ответ: 4,5
Задание
9
#2428
Уровень задания: Сложнее ЕГЭ
Найдите расстояние между двумя параллельными сторонами правильного шестиугольника со стороной (sqrt{108}).
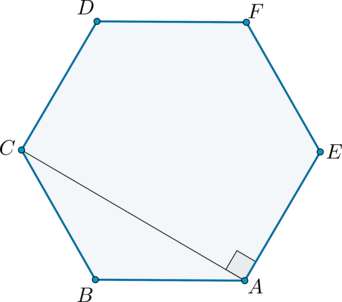
Рассмотрим правильный шестиугольник (ABCDFE) и в нем треугольник (ABC). Параллельными сторонами являются пары (AB) и (DF), (BC) и (FE), (CD) и (EA).
Помним, что угол правильного шестиугольника равен (120^circ).
(triangle ABC) равнобедренный ((AB=BC,)), следовательно, (angle
BAC=0,5cdot (180^circ-120^circ)=30^circ). Таким образом, (angle
CAE=120^circ-30^circ=90^circ).
Следовательно, (AC) – расстояние между сторонами (AE) и (CD) (по определению расстояние между двумя параллельными прямыми – отрезок, проведенный из любой точки одной прямой перпендикулярно ко второй прямой).
Найдем (AC) по теореме косинусов ((AB=BC=a=sqrt{108})):
(AC^2=a^2+a^2-2a^2cdot cos120^circ=2a^2(1-cos120^circ)=2cdot
108cdot left(1+frac12right)=3cdot 108 quad Rightarrow
)
(Rightarrow quad AC=sqrt{3cdot 108}=sqrt{3cdot 3cdot
36}=3cdot 6=18.)
Ответ: 18
Задание
10
#2431
Уровень задания: Сложнее ЕГЭ
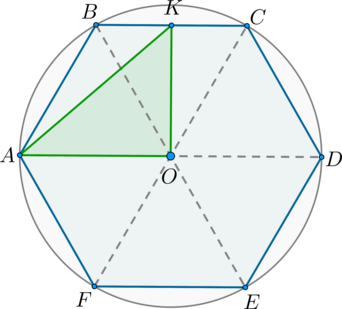
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Во сколько раз площадь этого шестиугольника больше площади треугольника (AOK), где (K) – середина стороны (BC).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=x).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, [S_{triangle AOK}=dfrac12cdot AOcdot OK=dfrac
x2cdot OK]
Площадь правильного шестиугольника равна сумме площадей шести правильных треугольников:
[S_{ABCDEF}=6cdot dfrac12cdot BCcdot OK=6cdot dfrac x2cdot OK]
Таким образом, [dfrac{S_{ABCDEF}}{S_{triangle AOK}}=6.]
Ответ: 6
Задание
11
#2432
Уровень задания: Сложнее ЕГЭ
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Найдите большую сторону треугольника (AOK), где (K) – середина стороны (BC=sqrt7) шестиугольника (ABCDEF).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=sqrt7).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, большая сторона в (triangle AOK) – это гипотенуза (AK). По теореме Пифагора из (triangle BOK) ((OK) также является в нем высотой):
[OK=sqrt{BO^2-BK^2}=sqrt{(sqrt7)^2-left(dfrac{sqrt7}2right)^2}=
dfrac{sqrt3}2cdot sqrt7]
Таким образом, по теореме Пифагора из (triangle AOK):
[AK=sqrt{AO^2+OK^2}=sqrt{(sqrt7)^2+left(dfrac{sqrt3}2cdot sqrt7right)^2}=
dfrac72=3,5.]
Ответ: 3,5

УСТАЛ? Просто отдохни
Определить сторону правильного шестиугольника можно легко при помощи этого калькулятора. Просто заполните любую ячейку, введя известное вам значение, – и под калькулятором отобразятся значения всех недостающих величин, а также формулы их нахождения. Это удобная шпаргалка по геометрии, которую полезно всегда держать под рукой!
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
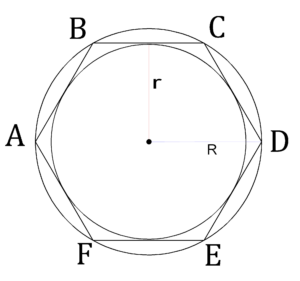
Радиус вписанной окружности (r)
Радиус описанной окружности (R)
Округление:
* — обязательно заполнить
Как найти сторону правильного шестиугольника
Шестиугольную — «гексагональную» — форму имеют, например, сечения гаек и карандашей, пчелиных сот и снежинок. Правильные геометрические фигуры такой формы имеют некую особенность, отличающую их от прочих плоских многоугольников. Заключается она в том, что радиус описанной около гексагона окружности равен длине его стороны — во многих случаях это значительно упрощает вычисление параметров многоугольника.

Инструкция
Если в условиях задачи дан радиус (R) описанной около правильного шестиугольника окружности, вычислять ничего не придется — эта величина тождественна длине стороны (t) гексагона: t = R. При известном диметре (D) просто поделите его пополам: t = D/2.
Периметр (Р) правильного шестиугольника позволяет вычислить длину стороны (t) простой операцией деления. В качестве делителя используйте число сторон, т.е. шестерку: t = Р/6.
Радиус (r) вписанной в такой многоугольник окружности связан с длиной его стороны (t) немного более сложным коэффициентом — удвойте радиус, а полученный результат разделите на квадратный корень из тройки: t = 2*r/√3. Эта же формула с использованием диаметра (d) вписанной окружности станет на одно математическое действие короче: t = d/√3. Например, при радиусе в 50 см длина стороны шестиугольника должна быть приблизительно равна 2*50/√3 ≈ 57,735 см.
Известная площадь (S) многоугольника с шестью вершинами тоже позволяет вычислить длину его стороны (t), но численный коэффициент, связывающий их, точно выражается через дробь из трех натуральных чисел. Две трети площади делите на квадратный корень из тройки, а из полученного значения извлекайте квадратный корень: t = √(2*S/(3*√3)). Например, если площадь фигуры составляет 400 см², длина ее стороны должна составлять примерно √(2*400/(3*√3)) ≈ √(800/5,196) ≈ √153,965 ≈ 12,408 см.
Длина окружности (L), описанной около правильного шестиугольника, связана с радиусом, а значит и с длиной стороны (t) через число Пи. Если он дана в условиях задачи, поделите ее величину на два числа Пи: t = L/(2*π). Скажем, если эта величина равна 400 см, длина стороны должна составлять приблизительно 400/(2*3,142) = 400/6,284 ≈ 63,654 см.
Этот же параметр (l) для вписанной окружности позволяет рассчитать длину стороны шестиугольника (t) вычислением соотношения между ней и произведением числа Пи на квадратный корень из тройки: t = l/(π*√3). Например, если длина вписанной окружности составляет 300 см, сторона шестиугольника должна иметь величину, примерно равную 300/(3,142*√3) ≈ 300/(3,142*1,732) ≈ 300/5,442 ≈ 55,127 см.
Видео по теме
Источники:
- сторона шестиугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Сторона правильного шестиугольника. Калькулятор и формулы
Определить сторону правильного шестиугольника можно легко при помощи этого калькулятора. Просто заполните любую ячейку, введя известное вам значение, – и под калькулятором отобразятся значения всех недостающих величин, а также формулы их нахождения. Это удобная шпаргалка по геометрии, которую полезно всегда держать под рукой!
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .
http://calcon.ru/storona-pravilnogo-shestiugolnika-kalkulyator-i-formuly/
http://shkolkovo.net/theory/77
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.