Как найти сторону треугольника зная его медиану - AvtoShod.ru

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Задача

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

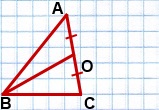
Дано: ∆ ABC,

AB=8 см,

BC=6 см,

BO — медиана, BO=√46 см.

Найти: AC.

Решение:

1) На луче BO отложим отрезок OD,

OD=BO.

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

4) По свойству диагоналей параллелограмма,

$[A{C^2} + B{D^2} = 2(A{B^2} + B{C^2})]$

$[A{C^2} + {(2sqrt {46} )^2} = 2({8^2} + {6^2})]$

$[A{C^2} + 184 = 200]$

$[A{C^2} = 16]$

Ответ: 4 см.

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

$[{(2{m_b})^2} + {b^2} = 2({a^2} + {c^2})]$

$[4m_b^2 = 2({a^2} + {c^2}) - {b^2}]$

$[m_b^2 = frac{{2{a^2} + 2{c^2} - {b^2}}}{4}]$

$[{{m_b} = frac{{sqrt {2{a^2} + 2{c^2} - {b^2}} }}{2}}]$

Источник

Как найти сторону треугольника, если известна его медиана и сторона

Информации о медиане и одной из сторон треугольника достаточно для нахождения его другой стороны, если он равносторонний или равнобедренный. В остальных случаях для этого необходимо знать угол между медианой и высотой.

Наиболее простой случай возникает, когда в условии задачи дан равнобедренный треугольник с некоторой стороной a. Две боковые стороны такого треугольника равны, а все медианы пересекаются в одной точке. Кроме того,в равнобедренном треугольнике, проведенная к основанию, является и высотой, и биссектрисой. Соответственно, в треугольнике ABC возникнет треугольник BHC, и по теореме Пифагора можно будет вычислить HC — половину стороны AC:HC=√[(CB)^2-(BH)^2]Следовательно, AC=2√[(CB)^2-(BH)^2]В равнобедренном треугольнике уголα=γ, как это показано на рисунке.

Если в условии задачи приведено значение длины медианы равнобедренного треугольника, проведенной к его боковой стороне, решайте задачу несколько иным способом. Во-первых, медиана не перпендикулярна к боковой стороне фигуры, а во-вторых, формула зависимости между медианой и тремя сторонами выглядит следующим образом:ma=√2(c^2+b^2)-a^2По этой формуле найдите ту сторону, которую медиана делит пополам.

Если треугольник является неправильным, то информации о медиане и стороне недостаточно. Необходимо знать также угол между медианой и стороной. Чтобы решить задачу, вначале найдите по теореме косинусов половину стороны треугольника:c^2=a^2+b^2-2ab*cosγ, где c — сторона, которую нужно найти.Если получается так, что используя теорему косинусов, можно найти лишь только половину стороны, то тогдавычисляемое значение умножается на два. Например, дана медиана и прилежащая к ней сторона, между которыми находится угол. Противоположная углу сторона делится медианой пополам. Вычислив половину стороны по теореме косинусов, получим:BC = 2c, где c — 1/2 стороны BC

Решение прямоугольных треугольников является таким же, как и у любого неправильного треугольника, если нам не известны его углы, а дан лишь только угол между медианой и стороной. Узнав вторую сторону, уже можно найти и третьюпо теореме Пифагора. Такие задачи помогают искать помимо сторон и другие параметры треугольников. К ним относятся, например, площадь и периметр, которые вычисляются по заданным сторонам и углам.

Источник

Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.

По двум сторонам и медиане найти третью сторону треугольника — задача, обратная нахождению медианы треугольника по трем его сторонам.

Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.

Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.

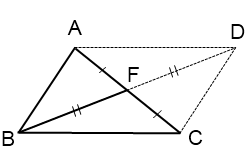
На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.

Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.

Переходим к решению конкретной задачи.

По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.

Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.

Источник

Все категории

Фотография и видеосъемка
Знания
Другое
Гороскопы, магия, гадания
Общество и политика
Образование
Путешествия и туризм
Искусство и культура
Города и страны
Строительство и ремонт
Работа и карьера
Спорт
Стиль и красота
Юридическая консультация
Компьютеры и интернет
Товары и услуги
Темы для взрослых
Семья и дом
Животные и растения
Еда и кулинария
Здоровье и медицина
Авто и мото
Бизнес и финансы
Философия, непознанное
Досуг и развлечения
Знакомства, любовь, отношения
Наука и техника

Как найти сторону равностороннего треугольника зная медиану????

1 ответ:

0

0

Допустим, имеем равносторонний треугольник ABC. Медиана, опущенная из вершины, делит сторону, на которую опускается, пополам. Т.е. медиана $BM= frac{1}{2} AC$ .
Помимо этого, медиана будет являться и высотой. Получаем два прямоугольных треугольника: ΔAMB и ΔBMC. Из них и узнаем сторону.
По теореме Пифагора:
BC²=BM²+MC²
BC²=BM²+BC²/4
BC²-BC²/4=BM²
3BC²/4=BM²
3BC²=4BM²
BC²=4BM²/3
BC= $sqrt{ frac{4BM^{2} }{3} }$

Как найти сторону треугольника, если известна его медиана и сторона

Как найти сторону равностороннего треугольника зная медиану????

Не пропустите также: