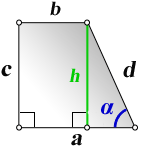
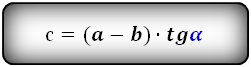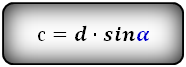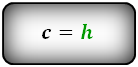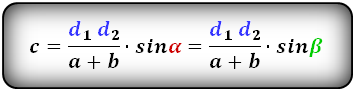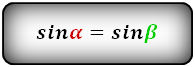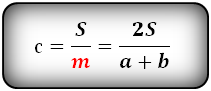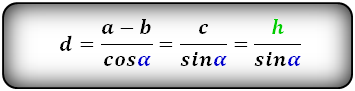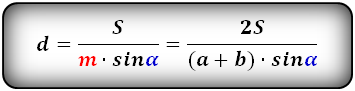1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
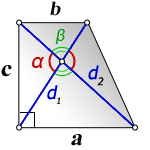
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
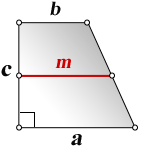
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
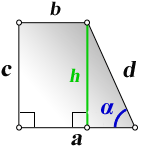
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
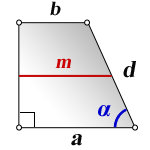
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 17 октября 2013
-
Обновлено: 13 августа 2021
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
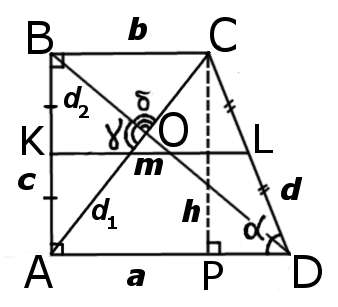 |
| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | — b b = | 2S | — a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:
| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
В прямоугольной трапеции , как впрочем и в любой другой трапеции 2 боковых стороны. Одна из боковых сторон в прямоугольной трапеции перпендикулярна обоим основаниям , и является высотой трапеции,обозначенной h.Остальные стороны пусть будут a и b — основания, и с — 2-я боковая сторона.Другие обозначения S-площадь трапеции.И вот формула боковой стороны h через площадь S :
h = S * 2 / (a + b) ,
Другая боковая сторона рассматривается из прямоугольного треугольника ,
где катеты h , (a-b) , а гипотенуза — искомая с :
c^2 = h^2 + (a- b)^2
В случае других данных , находить стороны можно по другим формулам.Но эти формулы чаще всего бывают. Ещё находят через углы , если они даны.
Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований. (рис.105.1)
m=(b+d)/2
Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру. Следовательно, площадь трапеции, которая обычно равна произведению высоты на среднюю линию, преобразуется в произведение боковой стороны на среднюю линию. (рис.105.2)
S=hm=am=(a(b+d))/2
Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой.
c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )
Периметр такой трапеции вычисляется также как обычной, сложением всех ее сторон.
P=a+b+c+d=a+b+d+√(a^2+〖(d-b)〗^2 )
Обе диагонали прямоугольной трапеции являются гипотенузами в прямоугольных треугольниках со стороной, перпендикулярной основаниям. Поэтому вычислить их становится возможным, используя теорему Пифагора. (рис.105.3)
d_1=√(a^2+b^2 )
d_2=√(a^2+d^2 )
Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований.
r=√bc/2
Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником
Примечание. Это часть урока с задачами по геометрии (раздел прямоугольная трапеция). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»
См. также: трапеция и ее свойства.
Прямоугольная трапеция
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
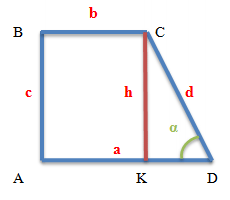
Формулы для прямоугольной трапеции
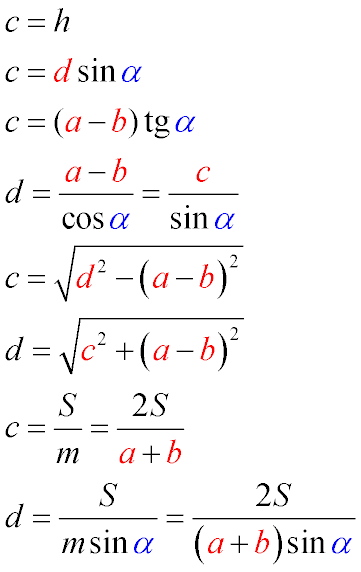
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона,
перпендикулярная
основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая
не перпендикулярна
основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции,
перпендикулярная
основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая
не перпендикулярна
основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2 + 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
0
Диагонали трапеции |
Описание курса
| Равнобокая (равнобедренная) трапеция