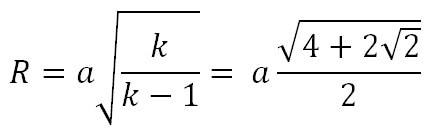В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
-
Расчет длины стороны
- Через радиус вписанной окружности
- Через радиус описанной окружности
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Через радиус вписанной окружности
Формула расчета
Через радиус описанной окружности
Формула расчета
Вычисление правильного восьмиугольника (многоугольник с восемью вершинами). Эта форма хорошо нам знакома, так как используется на некоторых дорожных знаках.
.
Поделиться расчетом:
Калькулятор восьмиугольника, введите одно известное значение
Длина стороны(a)
Меньшая диагональ(d1)
Средняя диагональ(e)
Большая диагональ(d3)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:

e = a * ( 1 + √2 )
f = a * √2 + √2
Высота = e = 2 * r
Р = 8 * а
S = 2 * a2 * ( 1 + √2 )
R = a / 2 * √4 + 2 * √2
r = a / 2 * ( 1 + √2 )
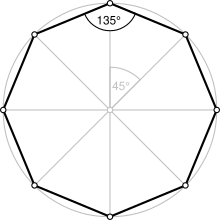
Угол: 135°, 20 диагоналей.
многоугольник с восемью сторонами
| Правильный восьмиугольник | |
|---|---|
 Правильный восьмиугольник Правильный восьмиугольник |
|
| Тип | Правильный многоугольник |
| Ребра и вершины | 8 |
| символ Шлефли | {8}, t {4} |
| диаграмма Кокстера | |
| группа симметрии | двугранный (D8), порядок 2 × 8 |
| Внутренний угол (градусов ) | 135 ° |
| Двойной многоугольник | Собственный |
| Свойства | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрии, восьмиугольник (от греческого ὀκτάγωνον oktágōnon, «восемь angles ») представляет собой восьмиугольник многоугольник или 8-угольник.
A правильный восьмиугольник имеет символ Шлефли {8}, а также может быть построен как квазирегулярный усеченный квадрат, t {4}, в котором чередуются два типа ребер. Усеченный восьмиугольник, t {8} — это шестиугольник, {16}. 3D-аналог восьмиугольника может быть ромбокубооктаэдром с треугольными гранями на нем, как замененные ребра, если считать восьмиугольник усеченным квадратом (а это так).
Содержание
- 1 Свойства общего восьмиугольника
- 2 Правильный восьмиугольник
- 2.1 Площадь
- 2.2 Окружной радиус и внутренний радиус
- 2.3 Диагонали
- 2.4 Конструкция и элементарные свойства
- 2.5 Стандартные координаты
- 2.6 Рассечение
- 3 Наклон восьмиугольника
- 3.1 Многоугольники Петри
- 4 Симметрия
- 5 Использование восьмиугольников
- 5.1 Другое использование
- 6 Производные фигуры
- 6.1 Связанные многогранники
- 7 См. Также
- 8 Ссылки
- 9 Внешние ссылки
Свойства общего восьмиугольника

Сумма всех внутренние углы любого восьмиугольника — 1080 °. Как и у всех многоугольников, внешние углы составляют 360 °.
Если квадраты построены полностью внутри или снаружи на сторонах восьмиугольника, то середины сегментов, соединяющих центры противоположных квадратов, образуют четырехугольник, который одновременно равнодиагонален и ортодиагональный (то есть диагонали которого равны по длине и расположены под прямым углом друг к другу).
восьмиугольник средней точки эталонного восьмиугольника имеет восемь вершин в средних точках сторон эталонного восьмиугольника. Если все квадраты построены внутри или снаружи на сторонах среднего восьмиугольника, то средние точки сегментов, соединяющих центры противоположных квадратов, сами образуют вершины квадрата.
Правильный восьмиугольник
A Правильный восьмиугольник представляет собой замкнутую фигуру со сторонами одинаковой длины и одинаковыми внутренними углами. Он имеет восемь линий отражательной симметрии и вращательной симметрии порядка 8. Правильный восьмиугольник представлен символом Шлефли {8}. Внутренний угол в каждой вершине правильного восьмиугольника равен 135 ° (3 π 4 { displaystyle scriptstyle { frac {3 pi} {4}}}

Площадь
Площадь правильного восьмиугольника с длиной стороны a определяется как
- A = 2 кроватки π 8 a 2 = 2 (1 + 2) a 2 ≃ 4.828 a 2. { displaystyle A = 2 cot { frac { pi} {8}} a ^ {2} = 2 (1 + { sqrt {2}}) a ^ {2} simeq 4.828 , a ^ { 2}.}
С точки зрения радиуса описанной окружности R, площадь равна
- A = 4 sin π 4 R 2 = 2 2 R 2 ≃ 2,828 R 2. { displaystyle A = 4 sin { frac { pi} {4}} R ^ {2} = 2 { sqrt {2}} R ^ {2} simeq 2.828 , R ^ {2}.}
В терминах апофемы r (см. Также вписанный рисунок ) площадь
- A = 8 tan π 8 r 2 = 8 (2 — 1) г 2 ≃ 3,314 г 2. { displaystyle A = 8 tan { frac { pi} {8}} r ^ {2} = 8 ({ sqrt {2}} — 1) r ^ {2} simeq 3.314 , r ^ { 2}.}
Последние два коэффициента заключают в скобки значение pi, площадь единичной окружности .

Площадь также можно выразить как
- A = S 2 — a 2, { displaystyle , ! A = S ^ {2} -a ^ {2},}
где S — длина восьмиугольника или вторая по длине диагональ; а — длина одной из сторон или оснований. Это легко доказать, если взять восьмиугольник, нарисовать квадрат снаружи (убедившись, что четыре из восьми сторон перекрываются с четырьмя сторонами квадрата), а затем взять угловые треугольники (это 45–45– 90 треугольников ) и размещает их прямыми углами внутрь, образуя квадрат. Края этого квадрата равны длине основания.
Учитывая длину стороны a, пролет S равен
- S = a 2 + a + a 2 = (1 + 2) a ≈ 2,414 a. { displaystyle S = { frac {a} { sqrt {2}}} + a + { frac {a} { sqrt {2}}} = (1 + { sqrt {2}}) a приблизительно 2.414a.}
Тогда размах равен соотношению серебра, умноженному на сторону, a.
Тогда площадь будет такой, как указано выше:
- A = ((1 + 2) a) 2 — a 2 = 2 (1 + 2) a 2 ≈ 4.828 a 2. { displaystyle A = ((1 + { sqrt {2}}) a) ^ {2} -a ^ {2} = 2 (1 + { sqrt {2}}) a ^ {2} приблизительно 4,828 a ^ {2}.}
Выраженная в размахе, площадь равна
- A = 2 (2 — 1) S 2 ≈ 0,828 S 2. { displaystyle A = 2 ({ sqrt {2}} — 1) S ^ {2} приблизительно 0,828S ^ {2}.}
Другая простая формула для вычисления площади:
- A = 2 a S. { displaystyle A = 2aS.}
Чаще известен промежуток S, и необходимо определять длину сторон a, как при разрезании квадратного куска материала на правильный восьмиугольник. Исходя из вышеизложенного,
- a ≈ S / 2,414. { displaystyle a приблизительно S / 2.414.}
Две конечные длины e с каждой стороны (длины сторон треугольников (зеленые на изображении), усеченные из квадрата), а также e = a / 2, { displaystyle e = a / { sqrt {2}},}
- e = (S — a) / 2. { displaystyle , ! e = (Sa) / 2.}
Окружной радиус и внутренний радиус
Окружной радиус правильного восьмиугольника с точки зрения длины стороны a равен
- R = (4 + 2 2 2) a, { displaystyle R = left ({ frac { sqrt {4 + 2 { sqrt {2}}}} {2}} right) a,}
и inradius равен
- r = (1 + 2 2) a. { displaystyle r = left ({ frac {1 + { sqrt {2}}} {2}} right) a.}
(это половина отношения серебра умноженное на сторону, a, или половину размаха, S)
Диагонали
Правильный восьмиугольник с точки зрения длины стороны a имеет три различных типа диагоналей :
- Короткая диагональ;
- Средняя диагональ (также называемая размахом или высотой), которая в два раза больше внутреннего радиуса;
- Длинная диагональ, которая в два раза превышает длину окружного радиуса.
Формула для каждого из них следует из основных принципов геометрии. Вот формулы для их длины:
Конструкция и элементарные свойства

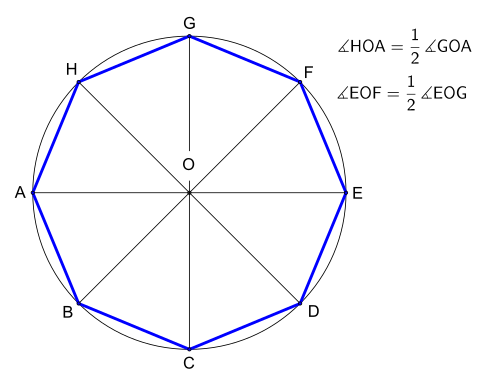
Правильный восьмиугольник по заданной описанной окружности может быть построен следующим образом:
- Нарисуйте круг и диаметр AOE, где O — центр и A, E — точки на описанной окружности.
- Нарисуйте еще один диаметр GOC, перпендикулярный AOE.
- (Попутно обратите внимание, что A, C, E, G — вершины квадрата
- Нарисуйте биссектрисы прямых углов GOA и EOG, образуя еще два диаметра HOD и FOB.
- A, B, C, D, E, F, G, H — это диаметры вершины восьмиугольника.
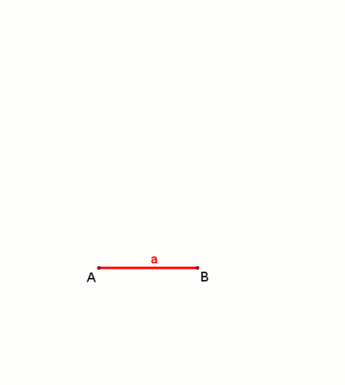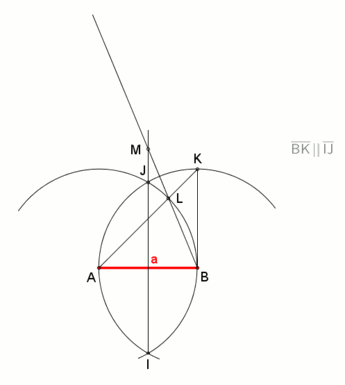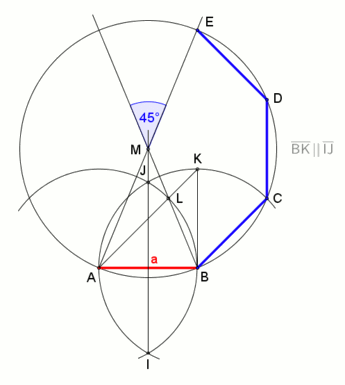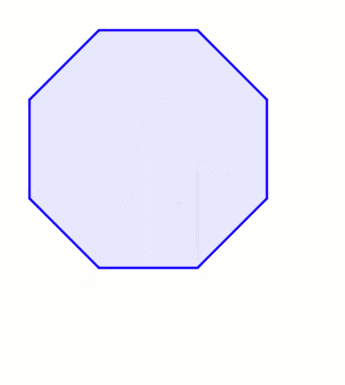
регулярный восьмиугольник можно построить с помощью линейки и компаса, так как 8 = 2, степень двойки :


Правильный восьмиугольник может быть построен из механических стержней. Нам нужно двенадцать стержней размера 4, три стержня размера 5 и два стержня размера 6.
Каждая сторона правильного восьмиугольника образует половину прямого угла в центре круга, соединяющего его вершины. Таким образом, его площадь можно вычислить как сумму 8 равнобедренных треугольников, что дает результат:
- Площадь = 2 a 2 (2 + 1) { displaystyle { text {Area}} = 2a ^ {2} ({ sqrt {2}} + 1)}
для восьмиугольника со стороной a.
Стандартные координаты
Координаты вершин правильного восьмиугольника с центром в начале координат и длиной стороны 2:
- (± 1, ± (1 + √2))
- (± (1 + √2), ± 1).
Рассечение
| 8-кубовое проекция | Рассечение 24 ромба | |
|---|---|---|
 |
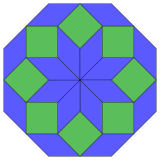 . Обычное . Обычное |
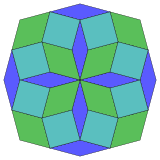 . Изотоксальное . Изотоксальное |
 |
 |
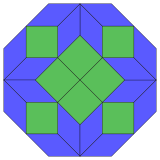
Коксетер утверждает, что каждый зоногон (двухметровый угольник, противоположные стороны которого параллельны и равной длины) может быть разрезан на m (m-1) / 2 параллелограмма. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Для правильного восьмиугольника m = 4, и его можно разделить на 6 ромбов, с одним примером, показанным ниже. Это разложение можно увидеть как 6 из 24 граней в плоскости проекции многоугольника Петри тессеракта . Список (последовательность A006245 в OEIS ) определяет количество решений как 8 по 8 ориентациям этого одного разреза. Эти квадраты и ромбы используются в мозаиках Амманна – Бенкера.
Рассеченный правильный восьмиугольник . Тессеракт . Тессеракт |
 . 4 ромба и 2 квадрата . 4 ромба и 2 квадрата |
Наклонный восьмиугольник

A наклонный восьмиугольник — это наклонный многоугольник с 8 вершинами и ребрами, но не находящихся в одной плоскости. Внутреннее пространство такого восьмиугольника в целом не определено. У косого зигзагообразного восьмиугольника вершины чередуются между двумя параллельными плоскостями.
A правильный скошенный восьмиугольник — это вершинно-транзитивный с равной длиной ребер. В 3-х измерениях это будет зигзагообразный восьмиугольник, который будет виден в вершинах и боковых гранях квадратной антипризмы с тем же D 4d, [2,8] симметрия, порядок 16.
многоугольники Петри
Правильный косой восьмиугольник — это многоугольник Петри для этих многомерных правильных и однородных многогранников, показанных в этих наклонных ортогональных проекциях из плоскостей A 7, B 4 и D 5Кокстера.
| A7 | D5 | B4 | |
|---|---|---|---|
 . 7-симплекс . 7-симплекс |
 . 5-полукуб . 5-полукуб |
 . 16-элементный . 16-элементный |
 . Тессеракт . Тессеракт |
Симметрия
Симметрия |
11 симметрий правильного восьмиугольника. Линии отражений синие по вершинам, пурпурные по краям, а порядок вращения указан в центре. Вершины окрашены в соответствии с их положением симметрии. |
Правильный восьмиугольник имеет симметрию Dih 8, порядок 16. Существует 3 двугранных подгруппы: Dih 4, Dih 2 и Dih 1. и 4 циклические подгруппы : Z 8, Z 4, Z 2 и Z 1, последнее подразумевает отсутствие симметрии.
Пример восьмиугольника по симметрии . r16 . r16 |
||
|---|---|---|
 . d8 . d8 |
 . g8 . g8 |
 . p8 . p8 |
 . g4 . g4 |
||
 . d2 . d2 |
 . g2 . g2 |
|
 . a1 . a1 |
На правильном восьмиугольнике существует 11 различных симметрий. Джон Конвей обозначает полную симметрию как r16 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или ребра (p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g за их приказы центрального вращения. Полная симметрия правильной формы — r16, симметрия не обозначена a1.
. Наиболее распространенными восьмиугольниками высокой симметрии являются p8, изогональный восьмиугольник, построенный из четырех зеркал. может чередовать длинные и короткие края, и d8, изотоксальный восьмиугольник, построенный с равными длинами ребер, но вершинами с чередованием двух разных внутренних углов. Эти две формы являются двойными друг другу и имеют половину порядка симметрии правильного восьмиугольника.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как направленные ребра.
Использование восьмиугольников

Восьмиугольная форма — это используется как элемент дизайна в архитектуре. Купол Скалы имеет характерный восьмиугольный план. Башня Ветров в Афинах — еще один пример восьмиугольной конструкции. Восьмиугольный план также использовался в церковной архитектуре, такой как Св. Георгия, Аддис-Абеба, Базилика Сан-Витале (в Равенне, Италия), Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий, Церковь Zum Friedefürsten (Германия) и ряд восьмиугольных церквей в Норвегии. Центральное пространство в Ахенском соборе, Каролингской Палатинской капелле, имеет правильную восьмиугольную планировку. Использование восьмиугольников в церквях также включает меньшие элементы дизайна, такие как восьмиугольная апсида Собора Нидарос.
Такие архитекторы, как Джон Эндрюс использовали восьмиугольную планировку этажей в зданиях для функциональное отделение офисных площадей от строительных служб, в частности, штаб-квартиры Intelsat в Вашингтоне, округ Колумбия, в Канберре, и офисов Octagon в Парраматта, Австралия.
Другое применение
Зонты часто имеют восьмиугольный контур.
Знаменитый ковер «Бухара» включает восьмиугольный мотив «слоновьей ноги».
План улиц и кварталов Барселоны в районе Эшампле основан на неправильных восьмиугольниках
Джангги использует восьмиугольные части.
Японские лотерейные автоматы часто имеют восьмиугольную форму.
Знак остановки, используемый в англоязычных странах, а также в большинстве европейских стран
Значок знака остановки с рукой посередине.
Триграммы Таоиста багуа часто расположены восьмиугольником
Знаменитая восьмиугольная золотая чаша с кораблекрушения Белитунг
Классы в Колледже Шимер традиционно хранятся вокруг восьмиугольных столов
Лабиринт Реймского собора квази-восьмиугольной формы.
Перемещение аналогового джойстика (ов) контроллера Nintendo 64, контроллера GameCube, Wii Nunchuk и Classic Controller ограничен вращающейся восьмиугольной областью, что позволяет ручке перемещаться только в восьми различных направлениях.
Производные числа
Родственные многогранники
восьмиугольник, как усеченный квадрат, является первым в последовательности усеченных гиперкубов :
Усеченных гиперкубов| Изображение |  |
  |
  |
  |
  |
  |
  |
… |
|---|---|---|---|---|---|---|---|---|
| Имя | Восьмиугольник | Усеченный куб | Усеченный тессеракт | Усеченный 5-куб | Усеченный 6-кубик | Усеченный 7-кубический | Усеченный 8-кубический | |
| Диаграмма Кокстера | ||||||||
| Вершинная фигура | () v () |  . () v {} . () v {} |
 . () v {3} . () v {3} |
 . () v {3,3} . () v {3,3} |
() v {3,3,3} | () v {3,3,3,3} | () v {3,3,3,3,3} |
Как развернутый квадрат, он также является первым в последовательность расширенных гиперкубов:
Расширенные гиперкубы |
  |
  |
  |
  |
  |
  |
… |
| восьмиугольник | Ромбокубооктаэдр | Бугристая тессера ct | Стерифицированный 5-куб | Пятиугольный 6-куб | Hexicated 7-кубический | ||
См. также
Ссылки
Внешние ссылки
| Найдите octagon в Викисловаре, бесплатном словаре. |
Содержание
- Определение правильного многоугольника
- Элементы правильного многоугольника
- Диагонали n — угольника
- Внешний угол многоугольника
- Сумма внутренних углов
- Сумма внешних углов
- Виды правильных многоугольников
- Основные свойства правильного многоугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Доказательства свойств углов многоугольника
- Правильный n-угольник — формулы
- Формулы длины стороны правильного n-угольника
- Формула радиуса вписанной окружности правильного n-угольника
- Формула радиуса описанной окружности правильного n-угольника
- Формулы площади правильного n-угольника
- Формула периметра правильного многоугольника:
- Формула определения угла между сторонами правильного многоугольника:
- Формулы правильного треугольника:
- Формулы правильного четырехугольника:
- Формулы правильного шестиугольника:
- Формулы правильного восьмиугольника:
- Сторона правильного многоугольника через радиус описанной вокруг него окружности
- Шаг 1
- Шаг 2
- Шаг 3
Определение правильного многоугольника
Правильный многоугольник – это выпуклый многоугольник, у которого равны все стороны и углы.
Признаки правильного n-угольника
- a1 = a2 = a3 = … an-1 = an
- α1 = α2 = α3 = … αn-1 = αn
Примечание: n – количество сторон/углов фигуры.
Элементы правильного многоугольника
Для рисунка выше:
- a – сторона/ребро;
- α – угол между смежными сторонами;
- O – центр фигуры/масс (совпадает с центрами описанной и вписанной окружностей);
- β – центральный угол описанной окружности, опирающийся на сторону многоугольника.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника |
 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
 |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
 |
Число диагоналейn – угольника равно |
| Диагональ многоугольника |

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |

Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольники выпуклые многоугольники .
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n — 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n — 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.
Виды правильных многоугольников
- Правильный (равносторонний) треугольник
- Правильный четырехугольник (квадрат)
- Правильный пяти-, шести-, n-угольник
Основные свойства правильного многоугольника
- Все стороны равны:
a1 = a2 = a3 = … = an-1 = an2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O4. Сумма всех углов n-угольника равна:
180° · (n — 2)
- Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
- В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Свойство 1
Внутренние углы в правильном многоугольнике (α) равны между собой и могут быть рассчитаны по формуле:
где n – число сторон фигуры.
Свойство 2
Сумма всех углов правильного n-угольника равняется: 180° · (n-2).
Свойство 3
Количество диагоналей (Dn) правильного n-угольника зависит от количества его сторон (n) и определяется следующим образом:
Свойство 4
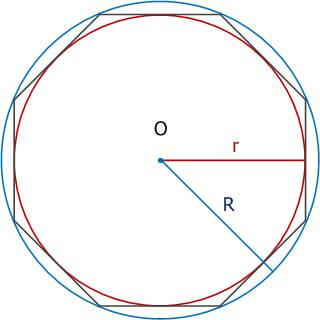
В любой правильный многоугольник можно вписать круг и описать окружность около него, причем их центры будут совпадать, в том числе, с центром самого многоугольника.
В качестве примера на рисунке ниже изображен правильный шестиугольник (гексагон) с центром в точке O.
Площадь (S) образованного окружностями кольца вычисляется через длину стороны (a) фигуры по формуле:
Между радиусами вписанной (r) и описанной (R) окружностей существует зависимость:
Свойство 5
Зная длину стороны (a) правильного многоугольника можно рассчитать следующие, относящиеся к нему величины:
- Площадь (S):
- Периметр (P):
- Радиус описанной окружности (R):
- Радиус вписанной окружности (r):
Свойство 6
Площадь (S) правильного многоугольника можно выразить через радиус описанной/вписанной окружности:
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов – угольникаn равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов – угольникаn , взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
- Формула стороны правильного n-угольника через радиус вписанной окружности:
- Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
- Формула площади n-угольника через длину стороны:
- Формула площади n-угольника через радиус вписанной окружности:
- Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
 |
| Рис.3 |
Формулы правильного треугольника:
- Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
- Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
- Формула радиуса вписанной окружности правильного треугольника через длину стороны:
- Формула радиуса описанной окружности правильного треугольника через длину стороны:
- Формула площади правильного треугольника через длину стороны:
- Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
- Формула площади правильного треугольника через радиус описанной окружности:
- Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Формулы правильного четырехугольника:
- Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
- Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
- Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
- Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
- Формула площади правильного четырехугольника через длину стороны:
S = a2
- Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
- Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
- Угол между сторонами правильного четырехугольника:
α = 90°
Формулы правильного шестиугольника:
Формула стороны правильного шестиугольника через радиус вписанной окружности:
Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
Формула площади правильного шестиугольника через длину стороны:
Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Формулы правильного восьмиугольника:
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
Угол между сторонами правильного восьмиугольника:
α = 135°
Сторона правильного многоугольника через радиус описанной вокруг него окружности
Сторону правильного многоугольника через радиус описанной вокруг него окружности можно найти по формуле
Где:
a – длина его стороны;
R – радиус описанной окружности;
n – число сторон многоугольника.
Формула стороны правильного многоугольника
Шаг 1
Рассмотрим правильный многоугольник А1А2А3…Аn.
Пусть его сторона будет равна a.
Опишем вокруг этого многоугольника окружность с центром в точке О и радиусом R.
Вывод формулы стороны правильного многоугольника.
Шаг 2
Соединим точку О с его вершинами. А1А2А3…Аn.
Рассмотрим треугольник ОА1А2.
Рассматриваемый треугольник будет равнобедренным, так как его стороны А1О и А2О – радиусы описанной окружности.
Проведем в треугольнике А1ОА2 высоту ОК.
Так как треугольник А1ОА2 равнобедренный, то высота будет медианой:
Вывод формулы стороны правильного многоугольника.
Шаг 3
Рассмотрим треугольник А1КО.
Этот треугольник прямоугольный, так как ОК – высота по построению.
Так как точка О – центр правильного многоугольника, то отрезки АnO являются биссектрисами углов этого многоугольника.
Таким образом, если углы многоугольника обозначим буквой α, то угол ОА1К будет равен:
По свойству углов правильного многоугольника, каждый угол равен:
Тогда угол ОА1К будет равен:
Из определения косинуса угла получим:
Отсюда:
Подставим в формулу значения, полученные выше и на шаге 2:
Умножим обе части уравнения на 2:
Воспользуемся формулами приведения
Так как А1О является радиусом описанной окружности, то сторона правильного многоугольника может быть найдена по формуле:
Вывод формулы стороны правильного многоугольника.
Восьмиугольник, виды, свойства и формулы.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
Восьмиугольник, выпуклый и невыпуклый восьмиугольник
Правильный восьмиугольник (понятие и определение)
Свойства правильного восьмиугольника
Формулы правильного восьмиугольника
Правильный восьмиугольник в природе, технике и культуре
Шестиугольник
Восьмиугольник, выпуклый и невыпуклый восьмиугольник:
Восьмиугольник – это многоугольник с восемью углами.
Восьмиугольник – это многоугольник, общее количество углов (вершин) которого равно восьми.
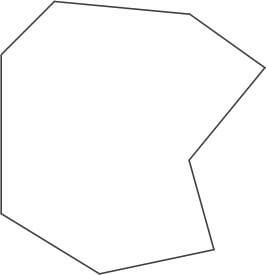
Восьмиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый восьмиугольник – это восьмиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый восьмиугольник
Рис. 2. Невыпуклый восьмиугольник
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°.
Правильный восьмиугольник (понятие и определение):
Правильный восьмиугольник (октагон) – это правильный многоугольник с восемью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный восьмиугольник – это восьмиугольник, у которого все стороны равны, а все внутренние углы равны 135°.
Рис. 3. Правильный восьмиугольник
Правильный восьмиугольник имеет 8 сторон, 8 углов и 8 вершин.
Углы правильного восьмиугольника образуют восемь равнобедренных треугольников.
Правильный восьмиугольник можно построить с помощью циркуля и линейки: проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Свойства правильного восьмиугольника:
1. Все стороны правильного восьмиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7 = a8.
2. Все углы равны между собой и составляют 135°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = α8 = 135°.
Рис. 4. Правильный восьмиугольник
3. Сумма внутренних углов любого правильного восьмиугольника равна 1035°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного восьмиугольника O.
Рис. 5. Правильный восьмиугольник
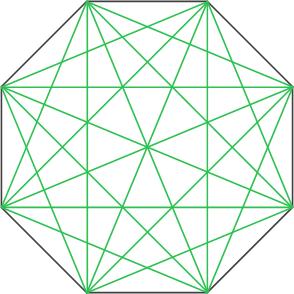
5. Количество диагоналей правильного восьмиугольника равно 20.
Рис. 6. Правильный восьмиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный восьмиугольник
Формулы правильного восьмиугольника:
Пусть a – сторона восьмиугольника, r – радиус окружности, вписанной в восьмиугольник, R – радиус описанной окружности восьмиугольника, k – константа восьмиугольника, P – периметр восьмиугольника, S – площадь восьмиугольника.
Формула константы правильного восьмиугольника:
Формула периметра правильного восьмиугольника:
Формулы площади правильного восьмиугольника:
Формулы радиуса окружности, вписанной в правильный восьмиугольник:
Формулы радиуса окружности, описанной вокруг правильного восьмиугольника:
Формулы стороны правильного восьмиугольника:
Правильный восьмиугольник в природе, технике и культуре:
В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного правильного восьмиугольника.
Форма правильного восьмиугольника часто используются в изобразительном искусстве, архитектуре. Например, Собор Святого Георгия (Аддис-Абеба, Эфиопия), Купол Скалы (Иерусалим, Израиль), башня Ветров (Афины, Греция), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий (Флоренция, Италия), Ахенский собор (Ахен, Германия), Капелла Карла Великого (Ахен, Германия).
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
7 187