Как найти сторону куба
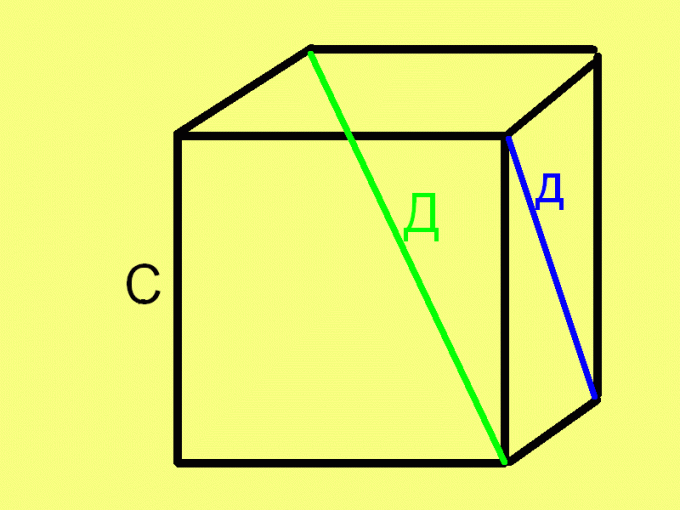
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней называются его ребрами, а точки пересечения ребер – вершинами. Иногда можно услышать и такой «термин» как «сторона» куба. В зависимости от конкретной ситуации под этим понятием может подразумеваться как грань куба, так и его ребро.В быту и играх (при использовании кубика в качестве игральной кости) стороной куба обычно называют его грань. Если же найти сторону куба пытается ученик, то наверняка требуется определить длину его ребра (куба, а не ученика).
Куб настолько симметричная фигура, что для нахождения его стороны (ребра) достаточно знать хотя бы один из основных параметров куба. К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «большой диагонали»).Чтобы найти сторону куба если известна площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту зависимость можно записать в следующем виде:С = √П, где:С – длина стороны (грани) куба,
П — площадь грани куба.Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба, и площадью, равной квадрату ребра.
Нахождение стороны (ребра) куба по заданному объему аналогично. Так как объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ³√Об, где Об – объем куба.
(³√ — функция извлечения кубического корня).
Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, разделенного пополам. В виде формулы это правило выглядит следующим образом:С = √(д²/2), где д – длина диагонали грани куба. Справедливость этой формулы вытекает из теоремы Пифагора, так как диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
Чтобы найти сторону (ребро) куба по его диагонали (именно диагонали куба, а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = √(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, так как диагональ куба, диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Как обнаружить сторону куба
Куб – одна из простейших объемных фигур. Он состоит из шести пересекающихся под прямым углом граней, представляющих из себя равные квадраты. Линии пересечения граней куба именуются его ребрами, а точки пересечения ребер – вершинами. Изредка дозволено услышать и такой «термин» как «сторона» куба . В зависимости от определенной обстановки под этим представлением может подразумеваться как грань куба , так и его ребро.В быту и играх (при применении кубика в качестве игральной кости) стороной куба традиционно называют его грань. Если же обнаружить сторону куба пытается ученик, то наверно требуется определить длину его ребра (куба , а не ученика).
Вам понадобится
- калькулятор
Инструкция
1. Куб настоль симметричная фигура, что для нахождения его стороны (ребра) довольно знать правда бы один из основных параметров куба . К ним относятся его объем, площадь грани, длина диагонали грани и длина диагонали куба (так называемой «крупной диагонали»).Дабы обнаружить сторону куба если вестима площадь его грани, извлеките из числового значения площади грани квадратный корень. В виде формулы эту связанность дозволено записать в дальнейшем виде:С = ?П, где:С – длина стороны (грани) куба ,П – площадь грани куба .Данная формула выводится из того факта, что грань куба представляет собой квадрат со стороной, равной ребру куба , и площадью, равной квадрату ребра.
2. Нахождение стороны (ребра) куба по заданному объему подобно. Потому что объем куба равен третьей степени (кубу) длины его ребра, то для определения длины ребра куба извлеките из его объема кубический корень. То есть воспользуйтесь формулой:С = ??Об, где Об – объем куба .(?? – функция извлечения кубического корня).
3. Для нахождения стороны (ребра) куба по диагонали его грани извлеките квадратный корень из квадрата диагонали, поделенного напополам. В виде формулы это правило выглядит дальнейшим образом:С = ?(д?/2), где д – длина диагонали грани куба . Честность этой формулы вытекает из теоремы Пифагора, потому что диагональ и два примыкающих ребра образуют равносторонний прямоугольный треугольник, где диагональ является гипотенузой, а ребра – катетами.
4. Дабы обнаружить сторону (ребро) куба по его диагонали (именно диагонали куба , а не грани), извлеките квадратный корень из трети квадрата длины этой диагонали. То есть, воспользуйтесь аналогичной предыдущей формулой:С = ?(Д^2/3).Эта формула также выводится на основе теоремы Пифагора, потому что диагональ куба , диагональ грани и ребро куба образуют прямоугольный (но, неравносторонний) треугольник.
Полезный совет
Для нахождения квадратных и кубических корней воспользуйтесь инженерным калькулятором. Дабы извлечь корень третьей степени возведите число в степень ?.
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
-
Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Куб. Формулы, признаки и свойства
Навигация по странице:
Определение куба
Грань куба
Ребро куба
Вершина куба
Центр грани куба
Центр куба
Ось куба
Диагональ куба
Диагональ грани куба
Объём куба
Площадь поверхности куба
Периметр куба
Сфера вписана в куб
Сфера описана вокруг куба
Свойства куба
Координати вершин куба
Единичный куб
Пересечение единичного куба плоскостью
Определение.
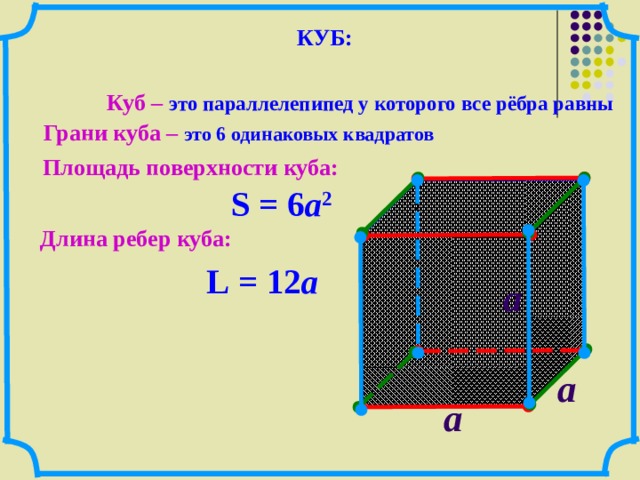
Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.
Определение. Грань куба — это часть плоскости, ограниченная сторонами квадрата.
— куб имеет шесть граней;
— каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;
— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.
Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.
— куб имеет двенадцать ребер;
— каждый конец ребра соединен с двумя соседними ребрами под прямым углом;
— ребра куба имеют одинаковую длину.
Определение. Вершина куба — это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.
— куб имеет восемь вершин;
— каждая вершина образована только тремя гранями и тремя ребрами.
Определение. Центр грани куба (O1) — это равноудалена точка от всех ребер грани куба.
Определение. Центр куба (O) — это равноудалена точка от всех граней куба.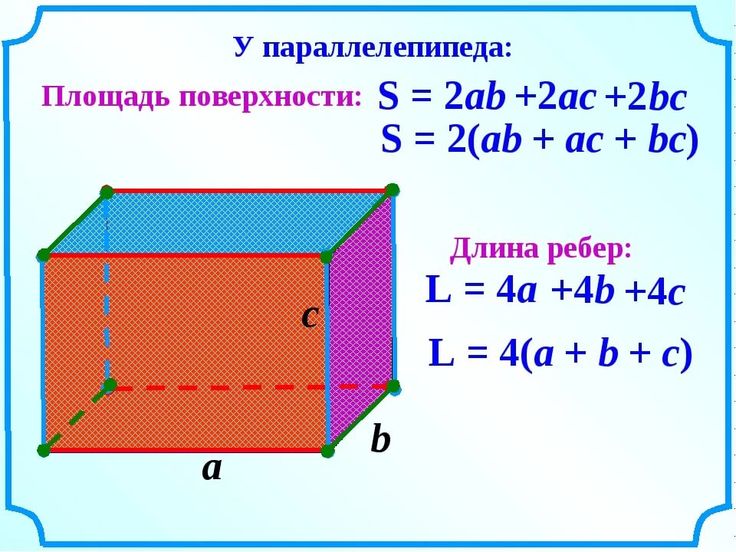
Определение. Ось куба (i) — это прямая, проходящая через центр куба и центры двух параллельных граней куба.
— куб имеет три оси;
— оси куба взаимно перпендикулярны.
Определение. Диагональ куба (d1) — отрезок, который соединяет противоположные вершины куба и проходит через центр куба.
— куб имеет четыре диагонали;
— диагонали куба пересекаются и делятся пополам в центре куба;
— диагонали куба имеют одинаковую длину.
Формула. Диагональ куба d1 через длину ребра a:
d1 = a√3
Определение. Диагональ грани куба (d2) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.
Формула. Диагональ грани d2 через длину ребра a:
d2 = a√2
Определение. Объём куба — это совокупность всех точек в пространстве, ограниченные гранями куба.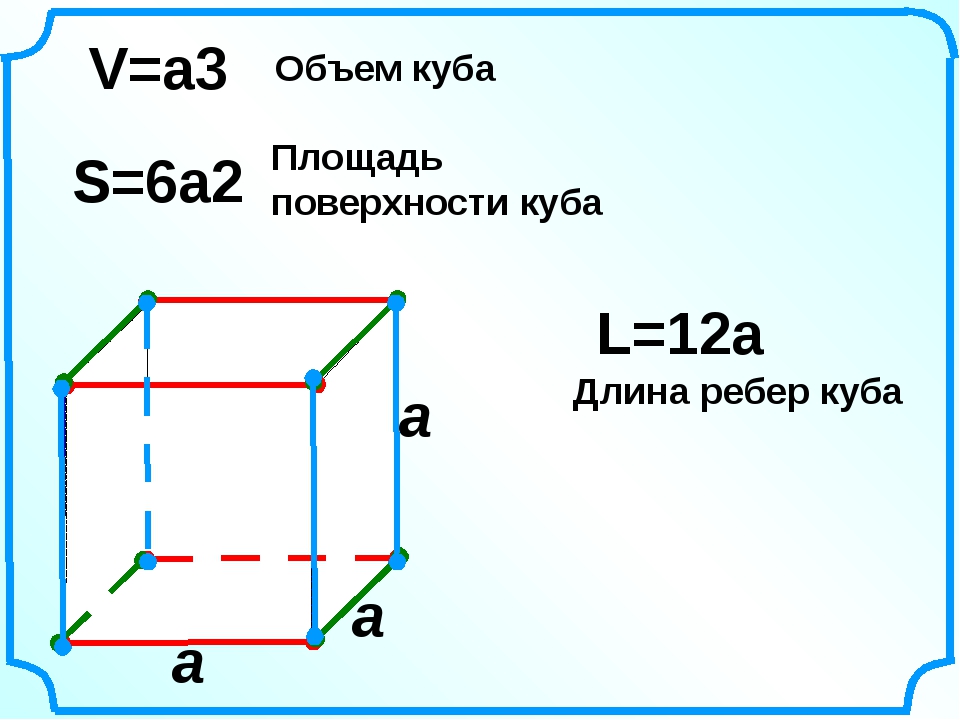
Формула. Объём куба через длину ребра a:
V = a3
Формула. Объём куба через длину диагонали куба d1:
Определение. Площадь поверхности куба — это совокупность плоскостей всех граней.
Формула. Площадь поверхности куба через длину ребра a:
S = 6a2
Определение. Периметр куба — это совокупность длин всех ребер куба.
Формула. Периметр куба P через длину ребра a:
P = 12a
Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.
— все шесть граней куба являются касательными плоскостями к вписанной сферы;
— радиус вписанной сферы равен половине длины ребра a.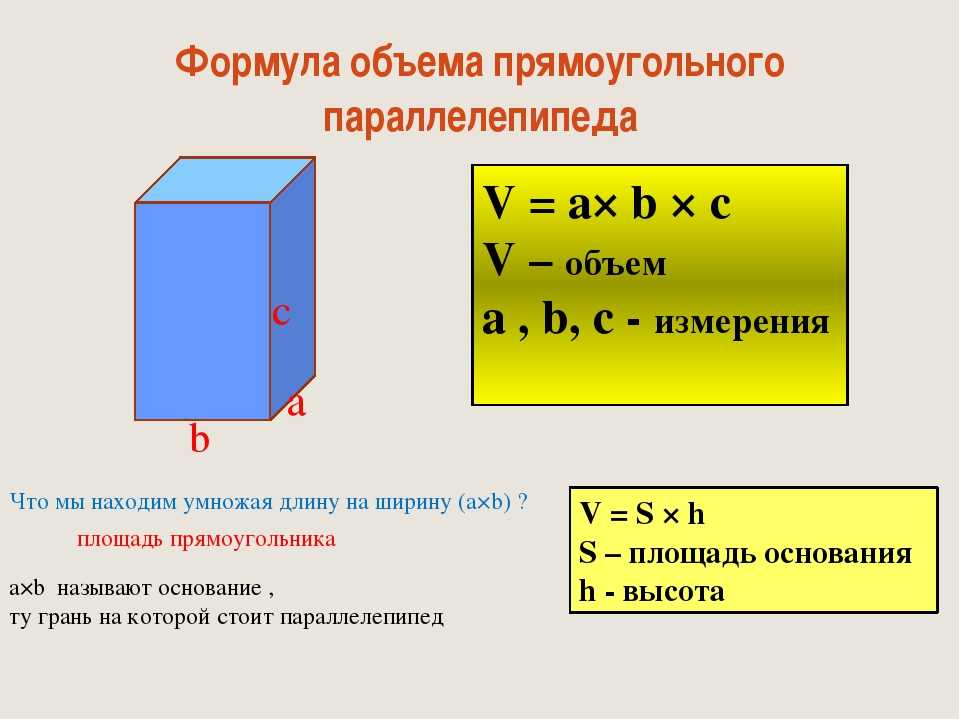
Формула. Радиус вписанной сферы r через длину ребра a:
Формула. Объема вписанной сферы V через длину ребра a:
Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.
— радиус описанной сферы равен половине длины диагонали (d1) куба.
Формула. Радиус описанной сферы R через длину ребра a:
Формула. Объема сферы описанной вокруг куба V через длину ребра a:
Свойства куба
1.
2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.
Координаты вершин куба
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:
A(a, 0, 0),
B(a, a, 0),
C(0, a, 0),
D(0, 0, 0),
E(a, 0, a),
F(a, a, a),
G(0, a, a),
H(0, 0, a).
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:
A(a, -a, -a),
B(a, a, -a),
C(-a, a, -a),
D(-a, -a, -a),
E(a, -a, a),
F(a, a, a),
G(-a, a, a),
H(-a, -a, a).
Определение.
Единичный куб — это куб, у которого длина ребер равна единице.
Пересечение куба плоскостью
1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.
2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a2√2. Эта плоскость делит куб две равные призмы.
3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a2(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.
4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a2√3/2 и объемом большей части — 5a3/6 и меньшей — a3/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.
Все таблицы и формулы
Что такое куб: определение, свойства, формулы
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
- Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
- Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1
, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.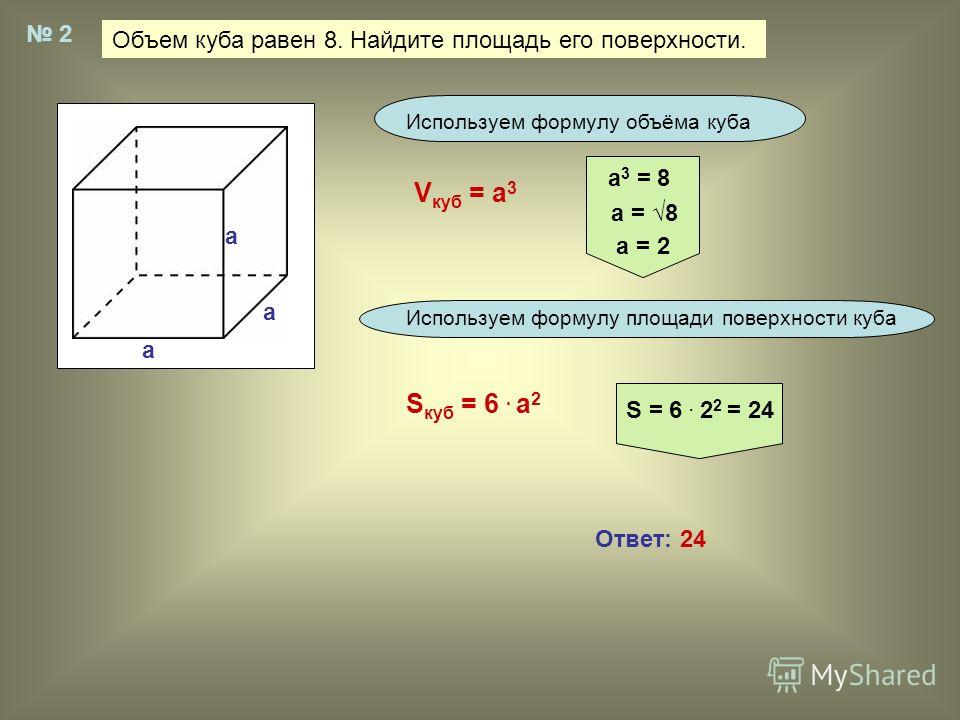
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA
1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Куб — свойства, виды и формулы » Kupuk.

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
-
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
-
прямая призма, все грани которой есть квадраты;
-
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ.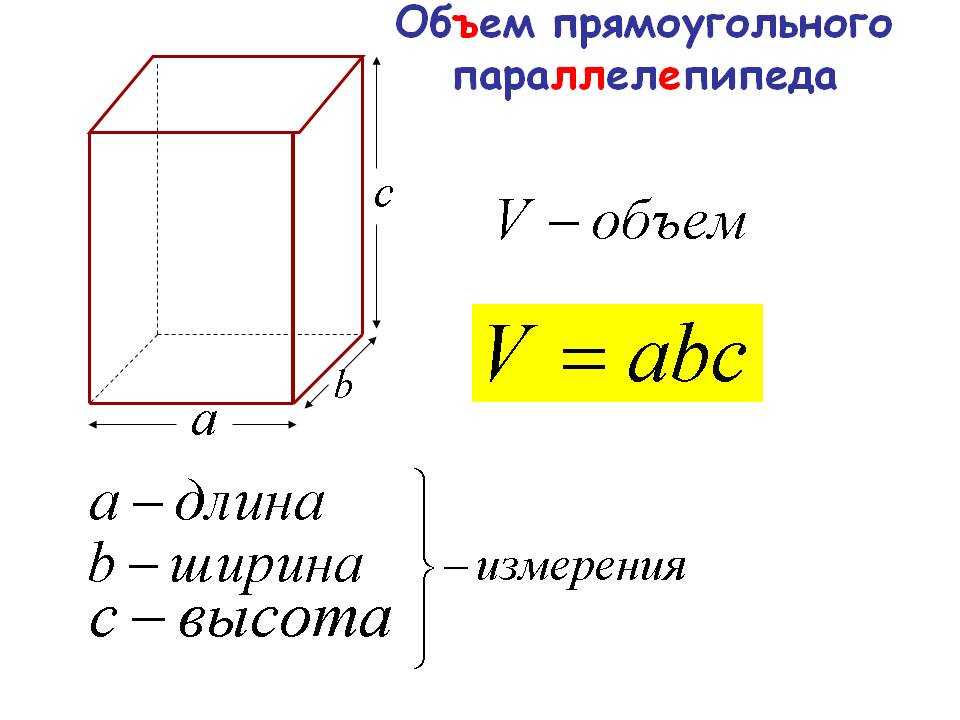
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач.
Прочие свойства:
-
у куба все грани равны, являются квадратами;
-
у куба все рёбра равны;
-
один центр и несколько осей симметрии.
- Объем куба (на основе длины стороны) = a 3 кубических дюймов, где a – длина стороны куба
- Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба
- Шаг 1: Рассмотрим любой квадратный лист бумаги.
- Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
- Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».
- Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
- Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
- Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2
- Куб имеет 12 ребер, 6 граней и 8 вершин.
- Все грани куба имеют форму квадрата, поэтому длина, ширина и высота одинаковы.
- Углы между любыми двумя гранями или поверхностями равны 90°.
- Противоположные плоскости или грани куба параллельны друг другу.
- Противоположные ребра куба параллельны друг другу.
- Каждая грань куба встречается с остальными четырьмя гранями.
- Каждая вершина куба встречается с тремя гранями и тремя ребрами.
- Объем куба (на основе длины стороны) = a 3 , где a — длина стороны куба
- Объем куба (по диагонали) = (√3×d 3 )/9 , где d — длина диагонали куба
- Длина диагонали грани куба = √2a единиц , где a = длина каждой стороны куба
- Длина главной диагонали куба = √3a единиц , где a = длина каждой стороны куба
- Куб Формула
- Платоновые тела
- Формы
- Твердые формы
- Плоские фигуры
-
Пример 1: Сколько воды хранится в одном кубике льда со стороной 5 дюймов?
Решение:
Дано,
Длина кубика льда = 5 дюймов
Количество воды в кубике льда = объему кубика
Следовательно, объем кубика льда = 5 × 5 × 5 в 3
= 125 в 3
Ответ: Количество воды во льду равно 125 в
0 13 900.
-
Пример 2: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.
Решение:
Длина стороны куба, a = 25 дюймов формула площади куба: A = 6a 2
A = 6 × 25 × 25
A = 3750
Ответ: Площадь поверхности куба составляет 3750 квадратных дюймов.
-
Пример 3: Найдите объем кубика Рубика длиной 5 дюймов.
Решение:
Чтобы найти объем кубика Рубика:
Длина стороны кубика = 5 дюймов ( дано)
Используя формулу куба,
объем = с × с × с = с 3Поставьте значения,
объем = 5 × 5 × 5 = 5 3 = 125
Ответ: Объем кубика Рубика равен 125 кубических дюймов.
- Куб имеет 12 ребер, 6 граней и 8 вершин.
- Все грани куба имеют квадратную форму.
- Общая площадь поверхности (TSA) = 6x 2
- Площадь боковой поверхности (LSA) = 4x 2
-
Все грани куба имеют квадратную форму.
-
Все грани и ребра равны.
-
Углы куба прямые.
-
Каждая из граней встречается с четырьмя соседними гранями.
-
Каждая из вершин встречается с тремя гранями и тремя ребрами.
-
Ребра, противоположные друг другу, параллельны и также равны.
-
Все 12 диагоналей на поверхности имеют площадь одинаковой величины
-
Все 4 внутренние диагонали равны
-
Каков объем куба 11,5 см?
-
Если объем куба равен 343 см 3 , то какова мера ребра куба?
Cube Formula — Что такое Cube Formula? Примеры
Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.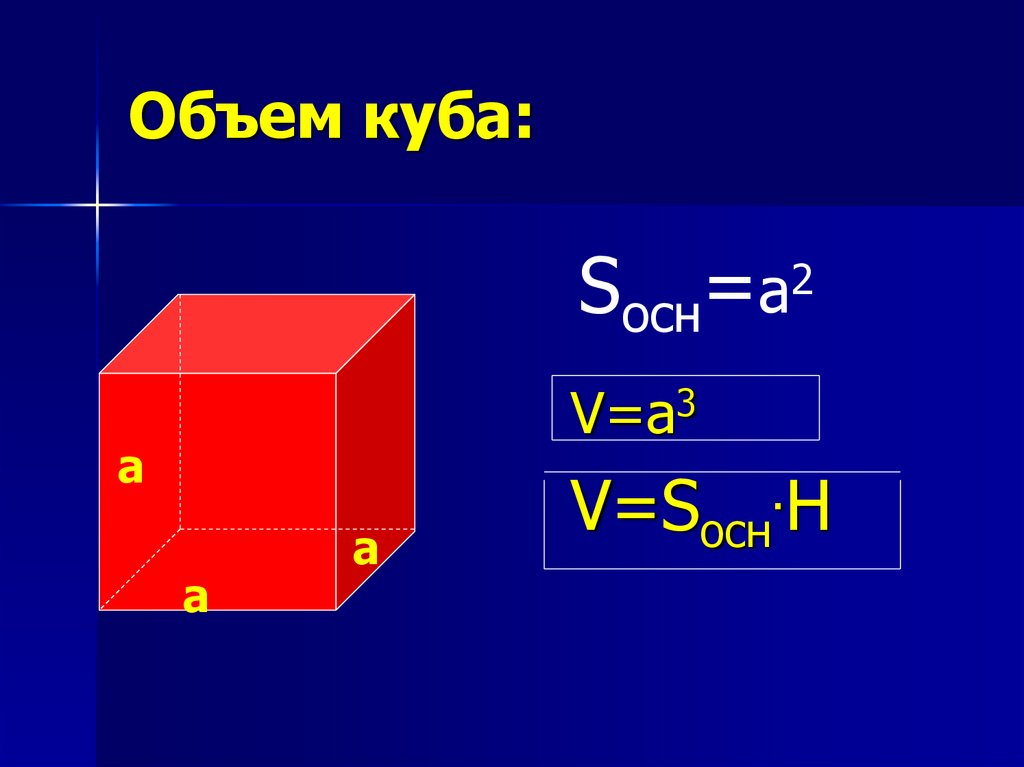
Что такое формула куба?
Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.
Формула куба
Объем куба
Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.
Боковая площадь куба
Боковая площадь куба равна сумме площадей всех боковых граней куба.
LSA куба = 4a 2
, где a — длина стороны.
Общая площадь куба
Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:
Общая площадь поверхности (TSA) куба = 6a 2
, где a — длина стороны.
Диагональ куба
Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.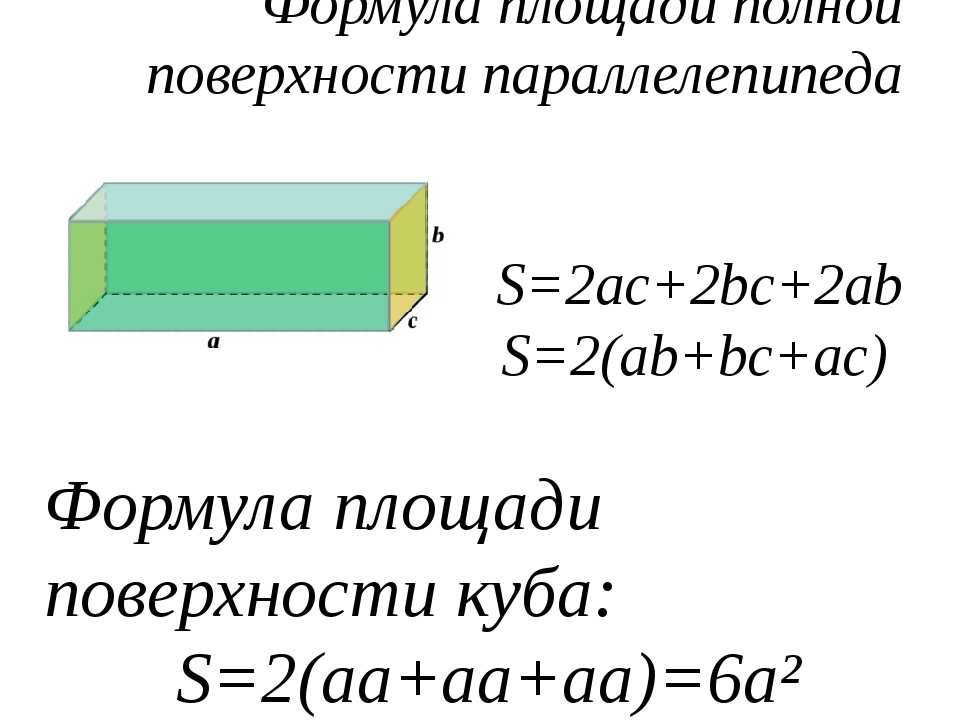
Диагональ куба = a√3
Давайте лучше разберемся с формулами куба на нескольких решенных примерах.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Примеры с использованием формулы куба
Пример 1: Найдите объем кубика Рубика длиной 4 дюйма.
Решение:
Чтобы найти объем кубика Рубика: кубик Рубика0003
Длина стороны куба = 4 дюйма (дано)
Используя формулу куба,
объем = с × с × с = с 3
Поместите значения,
объем = 4 × 4 × 4 = 4 3 = 64
Ответ: Объем кубика Рубика составляет 64 кубических дюйма.
Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба.
Решение:
Чтобы найти диагональ куба:
Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)
Используя формулу куба,
диагональ = a√3
Поместите значения,
Диагональ = 64√3 = 110,848 дюйма
Ответ: Диагональ куба равна 110,848 дюйма
Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.
Решение:
Длина стороны куба, a = 25 дюймов
Используя формулу площади куба, а именно: A = 6a 2
Поместите значения,
A = 6 × 25 × 25 = 3750 квадратных дюймов
Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.
Часто задаваемые вопросы о формуле куба
Что такое формула куба?
Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.
Как рассчитать диагональ куба по формуле куба?
Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .
Что такое s в формуле куба?
В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.
Как вывести формулу куба?
Чтобы вычислить объем по формуле куба,
Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2 × s = s 3
Чтобы вывести формулу поверхности куба,
Куб – формула, форма, определение, примеры
Куб – это трехмерный объект, имеющий 6 конгруэнтных квадратных граней. Размеры всех 6 квадратных граней куба одинаковы. Куб иногда также называют правильным шестигранником или квадратной призмой. Это одно из 5 платоновых тел. Некоторыми примерами куба из реальной жизни являются кубик льда, кубик Рубика, обычные игральные кости и т. Д. Давайте узнаем о кубе вместе с его формулами, несколькими решенными примерами и практическими вопросами здесь.
| 1. | Определение куба |
| 2. | Свойства куба |
| 3. | Кубическая сетка |
| 4. | Формула куба |
| 5. | Часто задаваемые вопросы о кубе |
Определение куба
Куб — это твердый трехмерный объект с шестью квадратными гранями, все стороны которого имеют одинаковую длину.
Куб Значение
Куб — это объемная объемная фигура, имеющая 6 квадратных граней. Это геометрическая фигура с 6 равными гранями, 8 вершинами и 12 равными ребрами. Некоторые примеры кубиков из реальной жизни — это игра в кости, кубики льда, кубик Рубика и т. д., которые мы видим вокруг себя.
Свойства куба
Куб считается особым видом квадратной призмы, так как все грани имеют форму квадрата и являются платоновыми телами.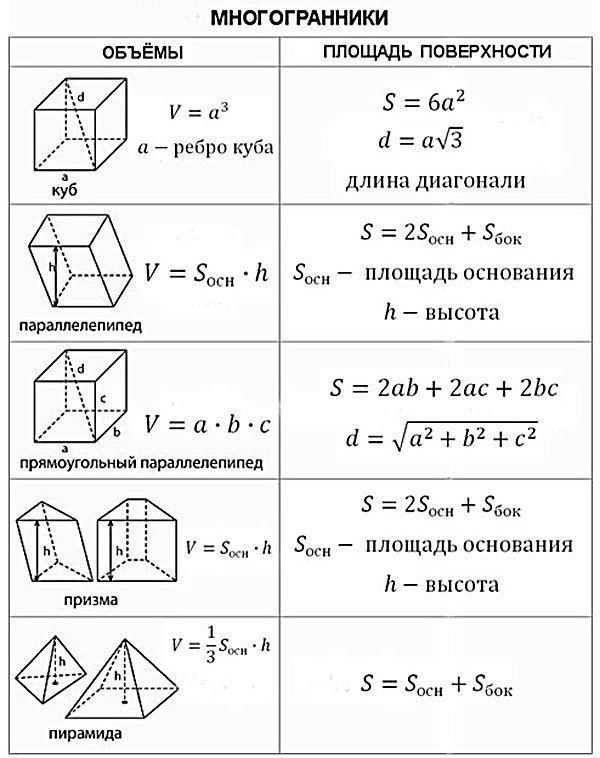
Кубическая сетка
Сетка куба формируется, когда трехмерная фигура с квадратными гранями сглаживается путем разделения по краям, превращая ее в двумерную фигуру. Через сетку куба мы можем ясно видеть шесть граней, то есть шесть квадратных граней, которые соединяются вместе по краям, образуя куб. Вот изображение для справки:
Куб Формула
Формула куба помогает нам найти площадь поверхности, диагонали и объем куба.
Площадь поверхности куба
Существует два типа площадей поверхности куба — Площадь боковой поверхности и Общая площадь поверхности
Площадь боковой поверхности куба
Площадь боковой поверхности куба равна сумме площадей всех боковые грани куба. У куба 4 боковые грани, поэтому сумма площадей всех 4 боковых граней куба равна его боковой поверхности. Боковая площадь куба также известна как площадь его боковой поверхности (LSA) и измеряется в квадратных единицах.
LSA куба = 4a 2
, где a — длина стороны. Для получения дополнительной информации вы можете проверить эту интересную статью о боковой площади формулы куба.
Общая площадь поверхности куба
Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз.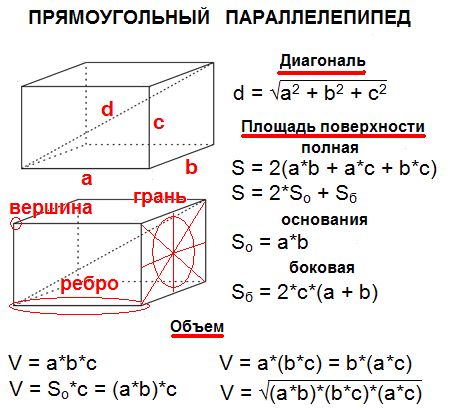
Общая площадь поверхности (TSA) куба = 6a 2
, где a — длина стороны. Для получения дополнительной информации вы можете ознакомиться с этой интересной статьей о площади поверхности куба.
Объем куба
Объем куба – это пространство, занимаемое кубом. Объем куба можно узнать, найдя куб длины стороны куба. Для определения объема куба существуют разные формулы, основанные на разных параметрах. Его можно рассчитать, используя длину стороны или размер диагонали куба, и он выражается в кубических единицах длины. Следовательно, две разные формулы для нахождения объема куба:
Вы можете узнать больше о формуле объема, прочитав эту интересную статью о объеме куба.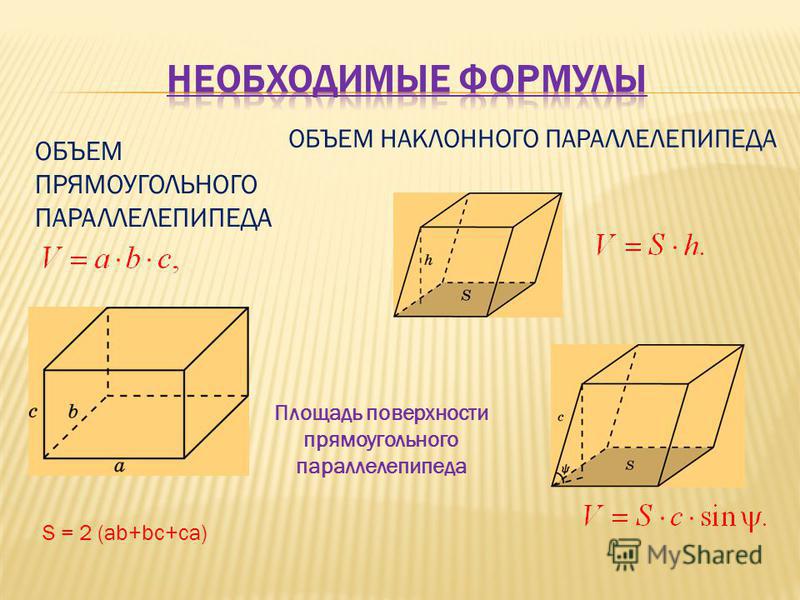
Диагональ куба
Диагональ куба — это отрезок, соединяющий две противоположные вершины куба. Длину диагонали куба можно определить по формуле диагонали куба. Это помогает найти длину диагоналей лица и главных диагоналей. Каждая диагональ грани образует гипотенузу образовавшегося прямоугольного треугольника. Куб имеет шесть граней (квадратной формы). На каждой грани есть две диагонали, соединяющие несмежные вершины. Следовательно, у нас есть двенадцать диагоналей граней и четыре главные диагонали, соединяющие противоположные вершины куба. Формула диагонали куба для расчета длины диагонали грани и диагонали основного тела куба определяется как 9.0003
Давайте посмотрим на несколько решенных примеров куба и его свойств для лучшего понимания.
☛Связанные темы
Ниже перечислены некоторые темы, связанные с кубом.
Примеры кубов
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Практические вопросы по Cube
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Cube
Что такое куб в геометрии?
В геометрии куб представляет собой трехмерную геометрическую фигуру с шестью конгруэнтными квадратными гранями.
Каковы два основных свойства куба?
Куб — это трехмерная фигура со многими геометрическими свойствами. Два основных свойства перечислены ниже.
Почему куб называют правильным шестигранником?
Правильный шестигранник представляет собой трехмерный объект с 6 конгруэнтными гранями. Таким образом, куб называется правильным шестигранником.
Какая формула площади боковой стороны куба?
Площадь поперечной стороны куба можно вычислить, зная длину его ребра. Площадь боковой стороны куба с длиной ребра ‘x’ равна 4×9.0020 2 кв. шт.
Как найти площадь боковой поверхности куба?
Площадь боковой стороны куба с длиной ребра ‘x’ можно получить, сложив площади 4-х боковых граней.
В чем разница между площадью поверхности и боковой поверхностью куба?
Площадь поверхности (или) общая площадь поверхности (TSA) куба представляет собой сумму площадей всех граней, тогда как площадь боковой поверхности (LSA) представляет собой только сумму 4 боковых граней куба. Если «x» — длина ребра куба, то
Что такое площадь поверхности и площадь?
Обычно термин «площадь» используется для обозначения пространства, ограниченного двухмерным объектом. «Площадь поверхности» используется для представления суммы площадей всех граней трехмерного объекта.
Что такое объем формулы куба?
Объем куба можно рассчитать по длине стороны. Объем куба 3 , где а — длина стороны куба.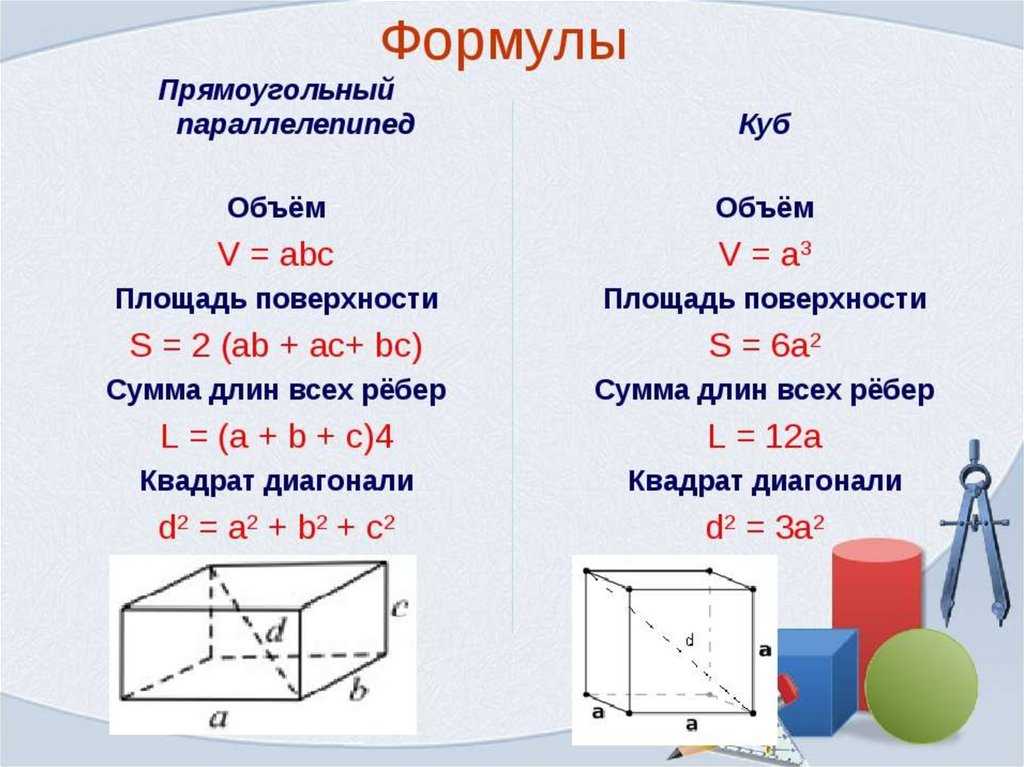
По какой формуле найти площадь основания куба?
Формула для нахождения площади основания куба: 2 , где а — длина стороны куба.
Что представляют собой 5 Платоновых тел?
Куб представляет землю, октаэдр представляет воздух, тетраэдр представляет огонь, икосаэдр представляет воду, а додекаэдр представляет вселенную.
Формула куба – объяснение, свойства и примеры решения
Нас окружают разные предметы, которые состоят из разных геометрических форм. Подумайте о детской игре с кубиками, игральными костями или кубиком льда. Что вы замечаете общего среди всего этого? Все они имеют форму куба, не так ли? В этой статье мы изучим, что такое куб? Объем формулы куба, площадь формулы куба, площадь поверхности формулы куба. Некоторыми из распространенных примеров кубика являются кубик льда, игральные кости, кубик Рубика.
Введение. Что такое куб?
Куб — это трехмерная фигура, состоящая из граней квадратной формы одинакового размера.
На приведенном ниже рисунке изображен куб, где l — длина, b — ширина, h — высота, и l = b = h. Длина, ширина и высота представляют ребра куба. И когда три ребра встречаются в точке, это называется вершиной.
(Изображение будет загружено в ближайшее время)
Свойства куба
Площадь поверхности куба Формула площади трехмерный объект. Поскольку трехмерный объект состоит из двухмерных граней, площадь поверхности представляет собой сумму площадей всех граней фигуры. Поэтому, чтобы найти площадь поверхности трехмерного объекта, мы должны сложить площади всех его граней. Мы можем использовать базовую формулу площади для вычисления его граней, поскольку они представляют собой простые 2D-фигуры,
Например, куб имеет шесть граней. Следовательно, площадь его поверхности будет равна сумме площадей всех шести граней.
В основном площадь поверхности можно классифицировать как:
Площадь изогнутой поверхности объекта – это площадь всех криволинейных поверхностей объекта.
Боковая поверхность предмета – это площадь всех граней предмета, за исключением площади его основания и вершины. Для куба площадь боковой поверхности будет равна сумме площадей четырех сторон, то есть умноженной на 4 стороны.
|
Площадь боковой поверхности = 4 × (край) 2 |
902
Куб — это трехмерный объект, поэтому пространство, занимаемое кубом, будет трехмерным.
Куб ограничен шестью квадратными гранями, поэтому площадь поверхности будет вычисляться путем сложения площадей всех шести квадратных граней. Следовательно, площадь поверхности куба по формуле равна 9.0003
|
Площадь поверхности куба = 6 (сторона) 2 |
. с точки зрения объема этого объекта. Объем твердого тела является произведением трех измерений, поэтому объем выражается в кубических единицах. Предположим, что объем куба измеряется произведением его длины, ширины и высоты.
Внутренняя часть полого объекта может быть заполнена воздухом или какой-либо жидкостью, которая принимает форму объекта. В таких случаях объем вещества, который может вместить внутренность предмета, называется вместимостью полого предмета. Таким образом, мы можем сказать, что объем объекта — это мера занимаемого им пространства, а вместимость объекта — это объем вещества, которое может вместить его внутренность.
А объем куба — это занимаемое им пространство. Объем формулы куба будет рассчитан как:
|
Volume = (side) 3 |
|
Length of Diagonal of Face of the Cube = √2(edge) |
|
Длина диагонала из куба = √3 (Edge) |
3
3
3
9000 9028
3 9000
Периметр = 12 (ребро)
Решаемые примеры
Пример 1. Найдите площадь поверхности куба, длина стороны которого равна 7 см.
Решение:
Указанная длина = края = 7 см
Ум.
= 6 × 49
= 294 см 2
Пример 2: Сторона кубического ящика равна 9 м. Найдите объем кубического ящика.
Решение:
DED, сторона = A = 9m
по формуле объема A Cube, мы знаем, что
V = A 3 11963
9
v = 3 1113
9
v = 3 1113
9
v = 3 1113
V = 3 111996469
v = 3 11996469
v = 3 113
V = 3 x 9 x 9
V = 729 кв.
Время викторины
Значение кубов в математике
Кубы — это трехмерные квадраты, которые многие считают символом геометрического совершенства. С какой стороны на него ни посмотри, он выглядит одинаково. Это часть геометрии в математике и чрезвычайно важна как глава. Понимание этого является ключом к пониманию других связанных концепций. Учащиеся должны быть внимательны при изучении кубиков, так как из этой главы возникнет много вопросов. Они могут перейти к формуле куба — объяснение, свойства и примеры решений и подробно разобраться в этом. На этой странице Веданту каждая концепция упрощена для понимания учеником.
Как найти площадь куба зная одну сторону?
Соответственно, площадь стороны куба – одной его грани, будет равна площади полной поверхности разделенной на шесть, а площадь боковой поверхности, состоящей из четырех граней, — двум третям площади полной поверхности куба. S=S_(п. п.)/6 S_(б.
Как можно вычислить куб?
Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Как найти ребро куба зная его объем?
2. Нахождение грани куба по его объему еще проще. Рассматривая, что объем куба равен кубу (третьей степени) длины ребра куба, получаем что длина ребра куба равняется корню кубическому (третьей степени) из его объема, т.
Как найти объем куба по площади?
Как найти объем куба – способ 2 Найти объем куба можно при помощи формулы площади поверхности куба: S=6a3. Скажем, площадь поверхности куба = 54 см2. Тогда a2 = 54/6 = 9.
Как найти площадь куба 4 класс?
Площадь куба — это сумма площади всех его сторон. Все стороны куба равны, поэтому, чтобы найти площадь куба, надо найти площадь одной из его сторон и умножить на 6.
Какая формула нахождения площади?
S = a × b, где a, b — длина и ширина прямоугольника. S = a × √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.
Как найти объем по длине ширине и высоте?
Как уже упоминалось, формула расчета объема выглядит следующим образом: V = Длина x Ширина x Высота; поэтому для получения объема необходимо просто перемножить все три стороны.
Сколько метров в 1 куб м?
Куби́ческий метр (кубометр) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС. Одному кубическому метру равен объём куба с длиной ребра 1 метр.
Как найти ребро куба?
Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.
Как найти ребро куба если известна его площадь?
Формулы
| Периметр куба (общая длина ребра) | O = | 12 × a |
|---|---|---|
| Площадь одной стороны | P = | a × a = a² |
| Площадь куба (поверхность) | Q = | 6 × P1 = 6 × a² |
| Объем куба | V = | a × a × a = a³ |
| Диагоналная (стороны/стены) | u2 = | a √2 ≈ a × 1,41 |
•6 сент. 2017 г.
Как найти объем по формуле?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Чему равен объем куба?
Объём куба равен произведению трех ребер куба или, так как, ребра куба равны, кубу (третьей степени) его ребра. где H — высота ребра куба.
Как найти площадь и объем?
площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.
Как найти площадь в физике 7 класс?
Чтобы определить площадь тела, используют формулы: площадь прямоугольника S можно рассчитать, умножив длину прямоугольника на ширину прямоугольника. S = l 1 ⋅ l 2 . Площадь треугольника S = ah 2 , где a — сторона, h — высота, проведённая к данной стороне.
Как найти площадь в 4 классе?
Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Как найти объем по массе?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Как рассчитать метр в кубе?
Кубические метры (м3) — это единица измерения объема, равная объему куба, стороны которого равны одному метру….Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5.
- = 12 × 2,5.
- = 30. Объем этой комнаты равен 30 м3.