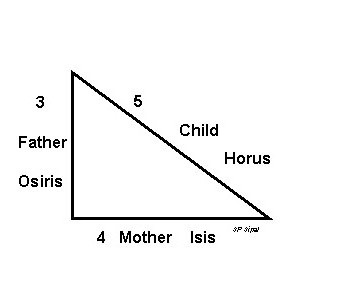
Египетский треугольник
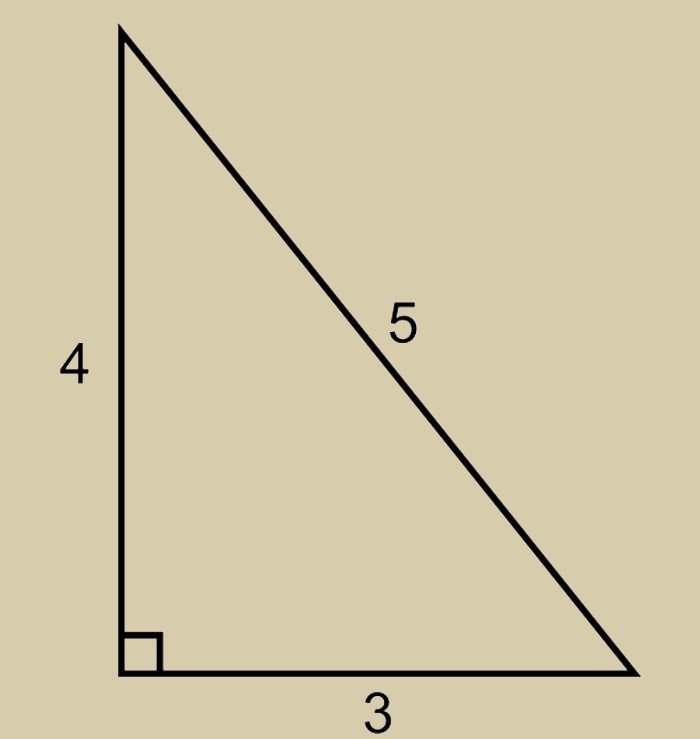
Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.
Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?
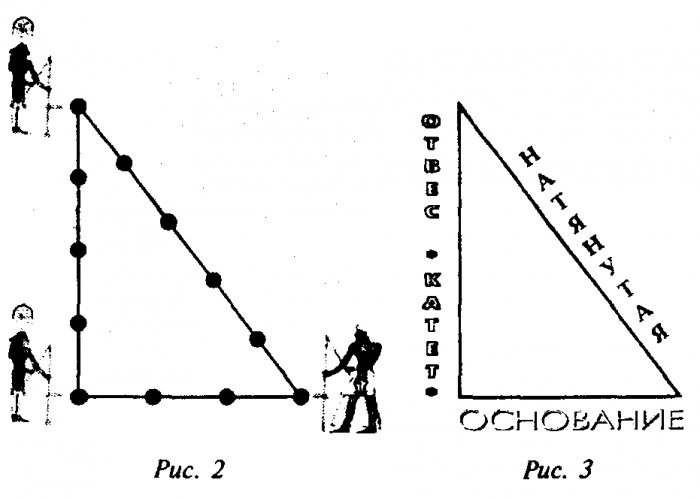
Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.
«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.
Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.
Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.
Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.
Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.
Египетский треугольник — загадка древности
Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.
История открытия
Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а
Применение
Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.
Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.
Доказательство
При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.
Египетский треугольник, его свойства
О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.
История египетского треугольника
Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.
Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Итоги
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.
http://www.syl.ru/article/136751/egipetskiy-treugolnik—zagadka-drevnosti
http://bouw.ru/term/egipetskiy-treugolynik
Египетский треугольник — это прямоугольный треугольник с соотношением сторон 3, 4, 5.
Об этом нам всем рассказывали в школе на уроках геометрии. Но что со всем этим делать? Давайте рассмотрим 3 сценария применения египетских треугольников в жизни.
1. Школьнику
Хитрые составители задач очень часто используют в своих заданиях египетские треугольники.
Простой пример:
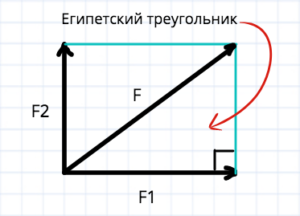
Две силы F1=8Н и F2=6Н приложены к телу под углом 90 градусов друг к другу. Найдите равнодействующую этих двух сил.
Равнодействующая будет находиться по правилу прямоугольника, и будет диагональю в этом прямоугольнике.
Как найти диагональ? Можно, конечно, решить по теореме Пифагора. Квадрат гипотенузы равен сумме квадратов катетов… Но если обратить внимание на то, что у нас прямой угол. Первый катет 6, или 2×3. Второй катет 8, что можно представить как 2×4. Можно сделать вывод что треугольник является египетским. А значит гипотенуза будет равна 2×5 или 10. Выходит равнодействующая сила будет равна 10 Н.
Все очень просто, а главное быстро, по этому египетские треугольники могут очень сильно облегчить Вам жизнь.Особенно на экзаменах по математике, где использование калькуляторов запрещено.
2. Строителю
Если вы уже закончили школу и подумываете как бы съехать подальше от родителей, то пришло время научится использовать египетский треугольник по назначению.
Древние египтяне применяли его в строительстве для получения прямых углов (Отсюда и название).
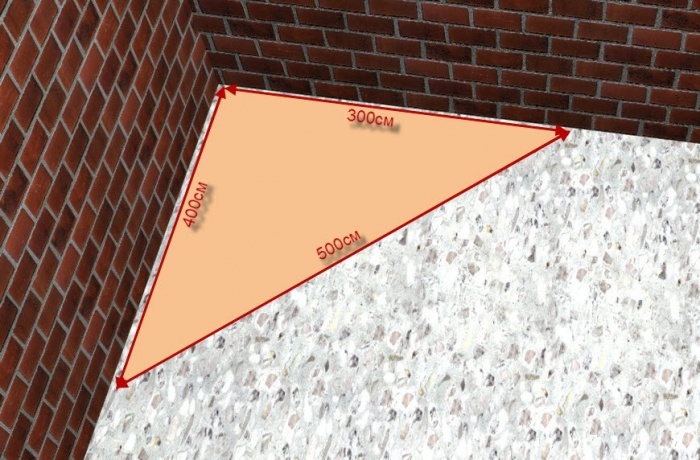
Берете веревку, делите ее на 12 равных частей. Главное не делите ее ножницами. Резать ничего не нужно, просто разметить. Узелки завязать можно или маркером нарисовать точки. Натягиваете веревку так чтоб получился треугольник со сторонами 3, 4, 5. Получаем идеально прямой угол для разметки фундамента под ваш будущий дом, гараж, баню или пирамиду.
3. Интеллигенту
Ну а если вы давно уже не школьник, и стройка вас никак не привлекает, в таком случае египетский треугольник может очень просто помочь вам интеллигентно выражать свои чувства и эмоции. Ну к примеру, когда ваш сын получил 2 по геометрии, или когда кот Мурзик пометил прямые углы вашего дома…
А как еще можно применять египетские треугольники в жизни??? Пишите в комментариях!
Египетский треугольник
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Свойства
- Особенностью такого треугольника, известной ещё со времён античности, является то, что все три стороны его целочисленны, а по теореме, обратной теореме Пифагора, он прямоуголен.
- Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
- Радиус вписанной в треугольник окружности равен единице.
История
Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до нашей эры греческие философы и общественные деятели активно посещали Египет.
Так, например, Пифагор в 535 году до нашей эры по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.
Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов египетскими землемерами и архитекторами, например, при построении пирамид.
Историк и математик Ван дер Варден ставил этот факт под сомнение, однако более поздние исследования его подтвердили[1].
В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности[2].
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.
Примечания
- ↑ Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматлит, 1959, С. 13, подстрочное примечание
- ↑ Египетский треугольник // Юсупов Э. Словарь терминов архитектуры, стр. 121. Издательство: Ленинградская галерея, 1994. ISBN 5-85825-004-1, 432 с.
См. также
- Теорема Пифагора
- Формула Герона
- Пифагорова тройка