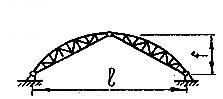
Арки впервые появились во II тысячелетии до н. э. в архитектуре Древнего Востока, в частности в Древней Месопотамии, где строительство кирпичных сооружений достигло высокого уровня. Широкое распространение также получили арки в архитектуре Древнего Рима.
В настоящее время арки применяются в павильонах, крытых рынках, ангарах, спортивных залах и т.п. большепролетных сооружениях. По затрате металла арки оказываются значительно выгоднее, чем балочные и рамные системы. Кроме того арки просты в изготовлении и монтаже.
Механика
Арка — это криволинейный брус плавного обриса, несущая строительная конструкция. В отличие от балки которая испытывает нормальное механическое напряжение, арка испытывает касательное механическое напряжение, из-за чего возникает горизонтальная опорная реакция (распор). От свода арка отличается лишь значительно меньшей шириной. Под вертикальной нагрузкой арка работает в большей степени на сжатие и в меньшей степени на изгиб.
Арки бывают бесшарнирные, двухшарнирные и трёхшарнирные; если опорные концы арки соединить стержнем (затяжкой, которая воспринимает горизонтальную реакцию), то получается арка с затяжкой.
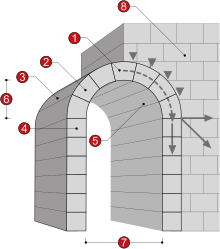
Арка из каменной кладки: 1. Замковый камень 2. Клинчатый камень 3. Внешняя поверхность свода (экстрадос) 4. Пятовый камень (импост) 5. Внутренний свод (интрадос) 6. Стрела подъёма 7. Пролёт 8. Опорная стена
Названия частей арки
- Замковый камень — поперечное сечение около вершины
- Клинчатый камень
- Внешняя поверхность свода (экстрадос)
- Пятовый камень (импост) — поперечное сечение около опоры, пята арки
- Внутренний свод (интрадос)
- Стрела подъёма — расстояние центра замкового камня арки от линии, которая соединяет центры двух пятовых камней арки
- Пролёт
- Опорная стена
Расстояние между центрами пят называется расчётной проймой. При увеличении стрелы подъёма уменьшается распор арки. Ось арки подбирают так, чтобы сжатие на изгиб было минимальным; тогда арка будет наиболее крепкой и стойкой.
Крепость арки зависит от её формы. Простейшие арки имеют форму полукруга, однако теоретически наиболее крепкими являются арки с формой параболы или цепной линии. Параболические арки впервые использовал испанский архитектор Антонио Гауди. Такие арки передают весь распор на опорную стену и не требуют дополнительных элементов.
Арки, перекрывающие несквозной проем, называются слепыми. Одной из целей этого является увеличение прочности стены при экономии материала. В древности известен приём, когда арка делалась для облегчения, например, когда перекрытие проёма в стене было выполнено в виде плоской арки, для разгрузки которой над нею делалась слепая арка.
Кирпичная кладка стен во дворце Августов. Древний Рим. Использованы разгрузочные арки.
Типы арок
 |
 |
 |
|
Треугольная |
Плоская сжатая арка |
Трёхлопастная арка |
 |
 |
 |
|
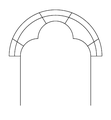
Подковообразная |
Трёхцентровая арка |
Эллиптическая арка |
|
|
|
|
|
Вогнутая арка |
Килевидная арка |
Опрокинутая килевидная арка |
 |
 |
 |
|
Круглая или полуциркульная |
Круглая пологая арка или сегментная |
Ползучая или косая арка |
 |
|
|
|
Стрельчатая |
Четырёхцентровая арка — «Тюдор» | Параболическая арка |
- По форме различают арки:
- аравийская — имеет повышенный центр построения, была распространена в зодчестве народов востока, в испано-мавританской архитектуре.
- аркбутан — арка с пятами на разных уровнях, наклонно передающая распор свода на внешнюю опору.
- вогнутая — перекрытая двумя дугами, обращёнными выпуклыми сторонами в пролёт.
- двулопастная — сложенная из двух малых арок одинаковых размеров, импосты и соединения которых расположены на одном уровне.
- двуцентровая — дуга, образованная из двух дуг одного и того же радиуса, пересекающихся в замке под тупым углом.
- диагональная — расположена в крестовом своде по диагонали квадрата или прямоугольника, то есть Нервюра, которую называют «ожива».
- эллиптичная — образована в пересечении частью эллипса.
- заплечная — устроенная над углублением в стене, тип круглой арки.
- обратная — с обращенной вниз выпуклостью дуги.
- зубчатая — с равномерным расположением по внутренней поверхности остроконечных выступов.
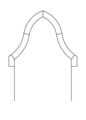
- килеподобная (килевидная или «ослиный хребет») — имеет вид поперечного разреза опрокинутого килевого судна, нашла применение в русском зодчестве.
- клинчатая — выложенная их клинчатых камней или из прямоугольных камней с клинчатыми швами.
- косая — см. ползучая.
- коробовая или эллиптическая — дуга, описанная из трёх, пяти, семи центров. Разновидностью её является седловидная арка.
- круговая (стиснутая) — описана полукругом из центра, расположенного ниже пят.
- угловая — то же самое, что и митровая.
- ланцетоподобная (копьеподобная) — образована двумя дугами, которые соединяются под углом и имеет формы стрельчатой равносторонней, стрельчатой стиснутой, стрельчатой плоской.
- ломаная — см. стрельчатая.
- лучковая (круговая) — с дугой менее полуокружности (одноцентровая).
- мавританская — то же самое, что и аравийская
- митровая — с двумя симметричными спадами в завершении.
- многолопастная — вид арки, составленной из трёх или большего числа кривых, пересекающихся под острым углом.
- овальная — образует в своде часть овала.
- выпукло-вогнутая — выгибы у пят обращены выпуклыми сторонами в середину пролёта и плавно переходят в одноцентровой или многоцентровой подъём по вертикальной оси.
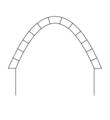
- параболическая — образует в своде часть параболы.
- опрокинутая — такая, в которой замок находится ниже пят. Выполняет функции разгрузочной и устраивается в нижней части стены.
- перспективная — концентрическая, уходящая внутрь стены уступами уменьшающихся радиусов, находит применение при оформлении порталов.
- полуциркульная или полукруглая — её дуга описана полуокружностью; наиболее распространённый вид арки.
- подвесная — состоит из двух дуг, точка пересечения которых расположена ниже вершины арки.
- подковообразная — то же самое, что аравийская.
- сводная — то же самое, что ланцетоподобная.
- стрельчатая — состоит из двух дуг, пересекающихся в замке под острым углом. Получила широкое применение в готической архитектуре. Различают стрельчатую арку, сжатую и ланцетовидную.
- плоская — со стрелой подъёма в несколько раз меньше пролёта.
- ползучая или «кобылья голова» — арка, имеющая опоры (пяты) на различных уровнях, например, под маршами лестниц.
- подпружная — вспомогательная арка, укрепляющая или поддерживающая различные конструкции сводов.
- портьерная — образована двумя или четырьмя дугами с центрами за пределами пролёта.
- притупленная — пологая стрельчатая с округлениями в пятах.
- пятилистная — навершие окна в виде пятилистника.
- разгрузочная — арка, заделанная в стене и распределяющая нагрузку от верхних частей здания на опоры, или наоборот, от отдельных опор на стенку фундамента.
- сжатая (лежачая) — завершенная горизонтальной перемычкой.
- скамеечка — беседка в виде триумфальной арки со сквозными решетчатыми стенками, к которым примыкают сиденья.
- ступенчатая — система арок в виде нескольких ярусов закомар.
- трёхлопастная — образована тремя полуокружностями, причём приподнятое среднее опирается на концы боковых, которые зеркально повторяют друг друга.
- трёхцентровая — полуовальная в разрезе, состоит из дуг трёх окружностей, из которых наибольшее среднее построенное радиусом из центра на оси пролёта. Две другие дуги прокладываются радиусами из точек, что находятся значительно выше.
- «тюдор» — пологая с заострённым верхом.
- воображаемая или фальшивая — арка, не дающая горизонтального распора, так как выложена путём горизонтального напуска камней.
- царская — расположенная в Царских вратах иконостаса христианского храма.
- щековая — подпружная крестового свода, расположена по бокам прямоугольника его плана. Окружает свод перпендикулярно к его образующей.
- упорная — см. аркбутан.
Арки возводятся также в виде отдельных сооружений:
- мемориальная — сооруженная в память о важном событии или исторической личности.
- триумфальная — подробнее см. триумфальная арка.
Полуциркульная (полукруглая) арка — арка, имеющая форму полуокружности, центр которой расположен на уровне пят арки.
Простейший и наиболее распространённый тип арки. Присутствует в зодчестве разных эпох, стран и стилей. Наиболее характерна для классической архитектуры, где она чаще всего бывает обрамлена архивольтом (от лат. arcus volutus — «обрамляющая дуга») или выделена рядом клинчатых камней с замковым камнем посередине. Обычно опирается на пилоны.
Лучковая арка — арка, имеющая форму дуги примерно в четверть окружности. В Древнем Риме арки такой формы служили перемычкой оконных проемов в жилых зданиях. Типичным примером применения лучковой арки является сегментный арочный мост.
 |
 |
 |
|
Римский мост с полуциркульными арками. Алькантара, Испания |
Нюрнберг. Замок на воде Обербюрг. Ворота в виде двух лучковых арок |
Собор Парижской Богоматери |
 |
 |
|
|
Мясной мост в Нюрнберге |
Большой Москворецкий мост в Москве |
На Востоке полукруглая арка претерпела наиболее сильную трансформацию, превратившись в так называемую стрельчатую, или ломаную арку, дуги которой пересекаются под углом.
По форме различают несколько видов стрельчатых арок:
- равносторонние арки, центры дуг которых находятся в пятах арок;
- сжатые арки, центры дуг которых находятся на горизонтальной линии, проходящей через пяты арок;
- плоские арки, центры дуг которых находятся ниже пят арок.
Природная арка. Формы в виде арки являются весьма частыми в природе, являясь лишь малой частью криволинейных объектов и поверхностей, что свойственны природным объектам. Они могут быть из камня, изо льда, из дерева. Арочные формы в природе повлияли, скорее всего, на применение их человеком в строительных конструкциях. Являясь зачастую проходом из одного места в другое, они стали нести и сакральный смысл, символизируя своеобразный портал в то место, где возможно ожидать чего-то нового и ранее неизведанного. Являясь продуктом эрозии, арочные каменные конструкции играют незначительную роль в горообразовании, изучение их позволяет получить дополнительную информацию о происходивших на земле процессах.
Иногда природные арочные образования служат в качестве реальных конструкций, так как по ним могут быть проложены действующие дороги. Примеры подобных арок можно найти в природных парках Carter Caves State Resort Park и Natural Bridge State Resort Park в Кентукки.
Согласно классификации национального парка Арчес (штат Юта, США), каменный проём должен иметь ширину не менее 3 футов (0,914 метра) и располагаться в достаточно большой стене, чтобы считаться аркой. При этом арки через естественные водотоки, а также через пересохшие русла, называются природными мостами. Отверстия в скалах, расположенные достаточно далеко от краёв и не влияющие на форму скалы, арками не считаются.
Расчёт арок
В основе расчёта арочных конструкций лежит расчёт кривого стержня, элемента отличного от прямой балки, у него ось представляет собой тот или иной тип кривой линии (ось — линия, проходящая через центры тяжести поперечных сечений элемента). С допустимым приближением касательные напряжения от поперечной силы для кривых стержней можно определять по той же формуле Журавского, что и для прямых балок:
,
где
Соответственно, условие прочности по касательным напряжениям для кривых стержней будет представляться следующим образом:
.
Напряжения в кривом стержне, вызываемые нормальной силой, нормальны к сечению и равномерно распределены по его площади, то есть:
,
где
Гиперболический закон распределения нормальных напряжений в криволинейном стержне от действия момента
Изгибающий момент, как и в прямой балке, вызывает в кривом стержне только нормальные напряжения. Распределение их по высоте сечения определяется следующей формулой:
,
где
Получается, что в отличие от прямой балки, где напряжения распределяются по линейному закону, в криволинейном стержне нормальные напряжения от момента распределяются по гиперболическомузакону. Из этого следует несколько важных выводов, а именно: при изгибе кривого стержня нейтральная ось не проходит через центр тяжести сечения; напряжения в наружных волокнах элемента меньше, чем при таком же изгибе прямой балки, а во внутренних волокнах — больше; рост напряжений по высоте сечения происходит с разной скоростью. Наибольшей величины напряжения достигают с внутренней стороны. Однако они достаточно быстро убывают по глубине. Если конструкция работает в статическом режиме и сделана из пластичных материалов, не подверженных хрупкому разрушению, то перенапряжения на самом краю сечения с внутренней стороны могут не представлять опасности.
Формула нормальных напряжений от момента будет иметь вид:
,
а формула полных нормальных напряжений в кривом стержне:
.
Радиус кривизны нейтрального слоя определяется из уравнения:
.
Из формул следует, что чем меньше отношение радиуса кривизны стержня к высоте его сечения, тем больше работа кривого стержня отличается от работы прямой балки. Когда же радиус оси намного превосходит размеры сечения, работа кривого стержня похожа на работу прямой балки и нормальные напряжения в этих случаях будут почти равны. Чаще всего арки в строительных конструкциях относятся ко второй категории кривых стержней. К первой же можно отнести разнообразные криволинейные детали: крюки, звенья цепей, колец и пр[1].
Деформации, возникающие в кривых стержнях, в общем случае определяются следующими выражениями:
где
В большинстве случаев, однако, влиянием кривизны для определения деформаций можно пренебречь.
Очертание оси арки может быть самым разнообразным, но чаще встречаются следующие виды:
Очертания осей арок
 |
 |
 |
|
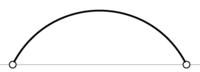
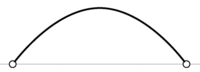
Циркульная (круговая) |
Параболическая |
Коробовая |
 |
 |
|
|
Треугольная |
«Ползучая» |
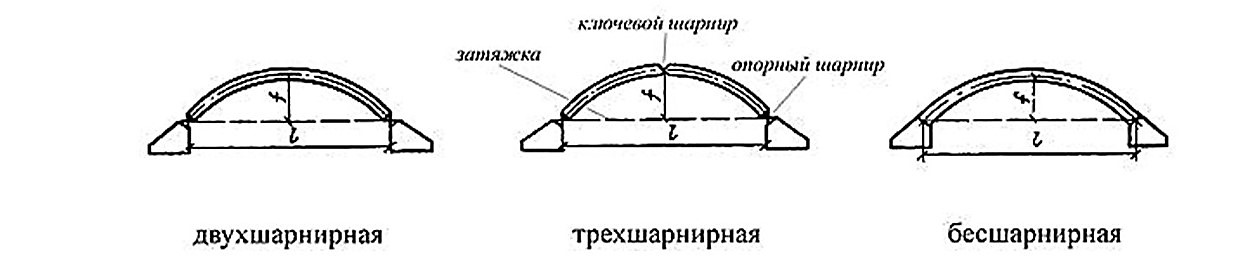
Наиболее распространёнными являются следующие типы расчётных схем арок:
Типы арок по статической работе
|
Трёхшарнирная арка |
Двухшарнирная арка |
Бесшарнирная арка |
 |
 |
 |
Каждый из типов имеет свои преимущества и недостатки, и выбор той или иной конструкции определяется инженером-проектировщиком исходя как из прочностных требований, так и из необходимости применения тех или иных материалов для арки, архитектурных задач, стоимости и местных условий строительства. Так, например, трёхшарнирная арка является статически определимой системой, в силу чего подобная конструкция не так чувствительна к температурным воздействиям и осадкам опор. Также трёхшарнирные арочные конструкции удобны с точки зрения монтажных работ и транспортировки, так как состоят из двух отдельных частей.
Однако наличие дополнительного шарнира приводит к большой разнице моментов по длине обоих частей, что, соответственно, требует дополнительного расхода материала. Противоположна ей в этом плане бесшарнирная арка, которая благодаря защемлению пят арок в опорах имеет наиболее благоприятное распределение моментов по длине и может быть изготовлена с минимальными сечениями. Но защемление в опорах, в свою очередь, приводит к необходимости устройства более мощных фундаментов, арка чувствительная как к перемещениям опор, так и к температурным напряжениям. Наибольшее распространение получила двухшарнирная арка. Являясь единожды статически неопределимой системой, она также имеет хорошее распределение моментов по длине и избавлена от необходимости устройства массивных опор.
Очертание арок выбирается близким к линии давления. При симметричной, равномерно распределенной по хорде арки нагрузке (в пологих арках ) наиболее выгодным является очертание арки по квадратной параболе. Параболу часто заменяют дугой окружности, что в пологих арках не приводит к существенному изменению усилий, но значительно упрощается проектирование и изготовление арок, поскольку при постоянной кривизне дуги достигается наибольшая стандартизация конструктивных элементов и узлов арки.
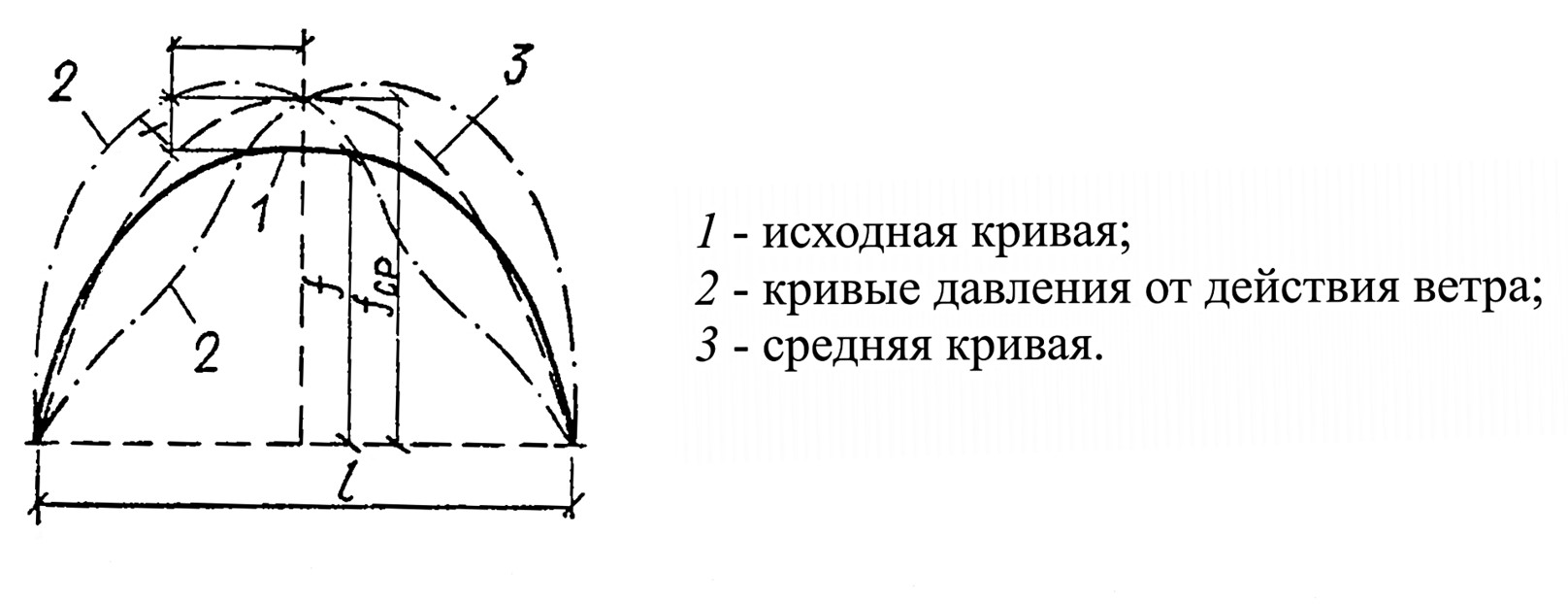
Для высоких арок с большим собственным весом целесообразно принимать очертание по цепной линии (катеноиду), Однако в высоких арках большие усилия вызывает ветровая нагрузка, которая может действовать с обеих сторон и давать две резко расходящиеся линии давления. В этом случае очертание арки целесообразно принимать по середине между двумя крайними линиями давления.
В многопролетных арках распоры смежных пролетов в значительной мере уравновешиваются, и средние опоры работают на изгиб только от односторонней временной вертикальной и ветровой нагрузок.
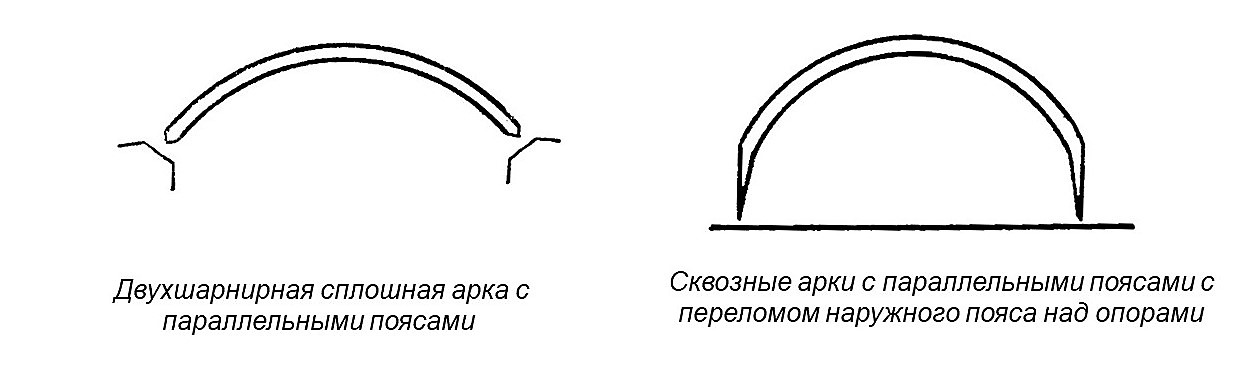
Двухшарнирные сплошные арки проектируют чаще всего с параллельными поясами.
Сквозные арки делают или с параллельными поясами или, при большой высоте арки, с переломом наружного пояса, который над опорами имеет вертикальные участки. Около опор пояса арок сближаются и заканчиваются опорным устройством – шарниром.
Высоту сечения сплошных арок назначают в пределах (1/50÷1/80) пролета, сквозных – в пределах (1/30÷1/60) пролета. Возможность применения в арках небольшой высоты сечения объясняется малой величиной изгибающих моментов.
Сплошные арки проектируются сварными с сечением в виде широкополочного двутавра (как и в сплошных рамах), в пологих арках продольные силы велики, поэтому стенку поперечного сечения арки можно назначать большей толщины, чем в раме.
Сквозные арки проектируются аналогично легким фермам. Пояса их компонуются из двух уголков или из двух легких швеллеров.
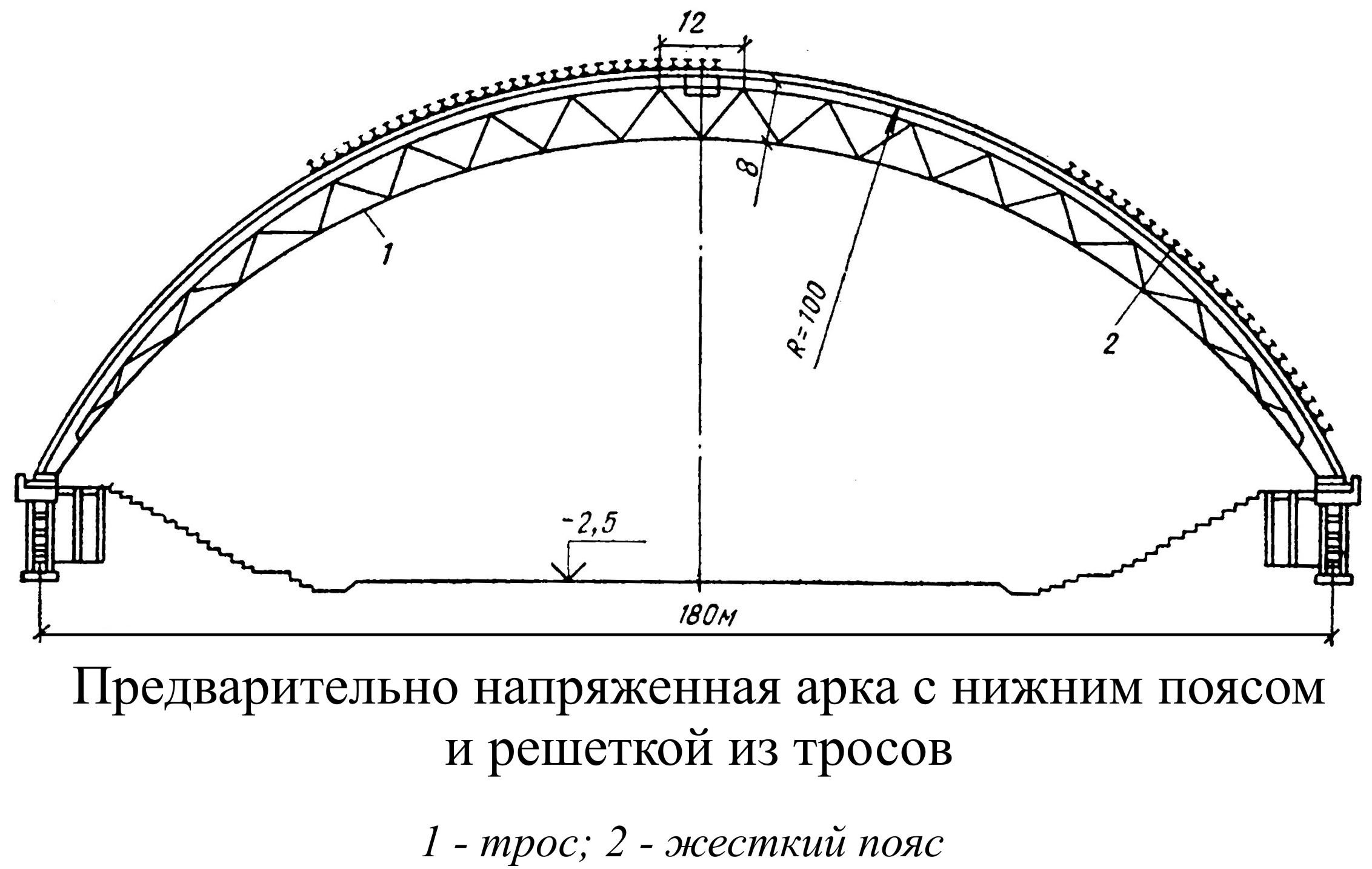
Сквозные арки в целях упрощения изготовления могут иметь ломаное очертание. В арках применяется также предварительное напряжение или регулирование усилий.
Одним из приемов рационального распределения усилий является принудительное смещение опорных узлов наружу после установки арки на опоры. При этом в нижнем поясе и раскосах арки возникает растягивающие напряжения, которые могут быть достаточными для погашения сжимающих напряжений от внешней нагрузки. В этом случае нижний пояс и решетка арки могут быть выполнены из стальных канатов, а верхний пояс – жестким.
Наиболее сложными конструктивными узлами в арках, так же как и в рамах, являются опорные и ключевые шарниры.
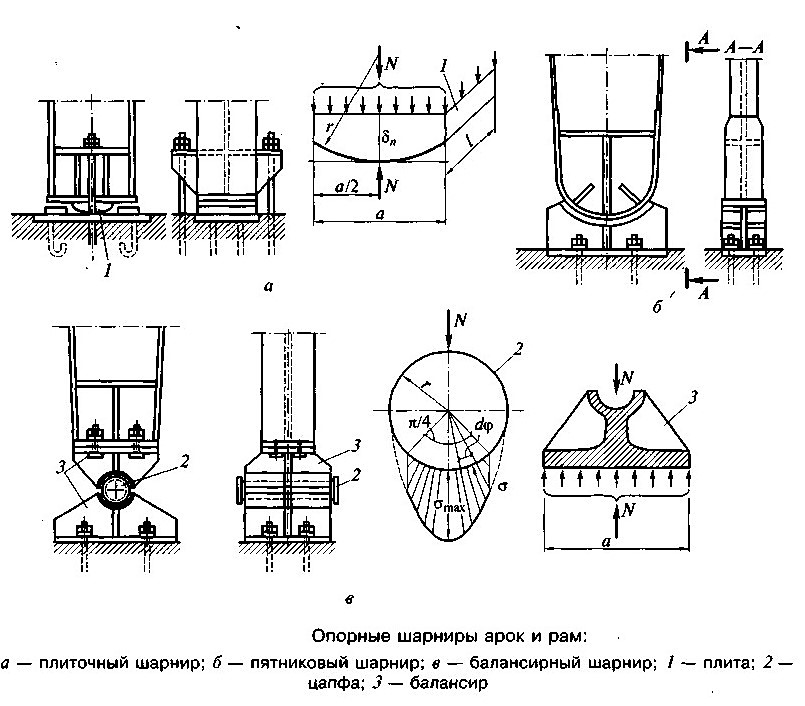
Опорные шарниры могут быть трех типов: плиточные, пятниковые и балансирные.

Пятниковые шарниры имеют специальное опорное гнездо – пятник, в который вставляется закругленная опорная часть арки. Пятник делают литым или сварным из листовой стали.
Балансирные шарниры применяют в тяжелых арках. Конструкция шарнира состоит из верхнего и нижнего балансиров, в гнезда которых укладывают плотно пригнанную цилиндрическую цапфу. Арку крепят к верхнему балансиру через плиту, которую приваривают к контуру опорного сечения арки и притягивают болтами к балансиру. Торцы опорных сечений арки обычно фрезеруют.
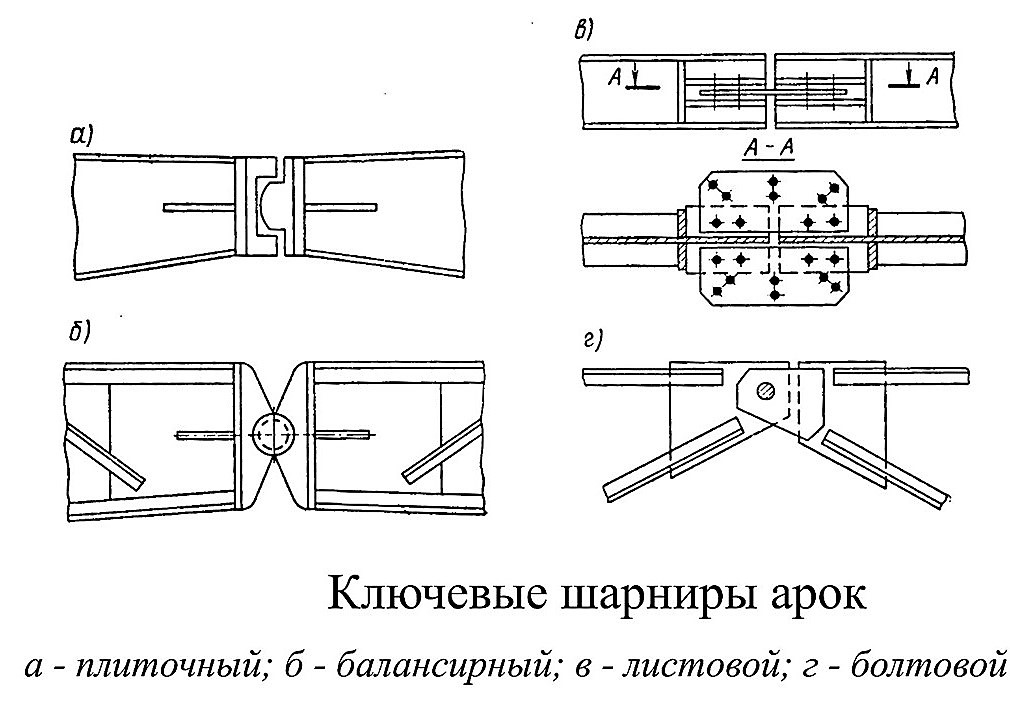
В ключе арки также могут быть применены плиточные или балансирные шарниры, которые проектируются аналогично опорным. В ключе легких арок могут применяться листовые или болтовые шарниры.
Арочные конструкции рассчитывают на вертикальные (собственный вес, снег) и ветровые нагрузки. Температурные воздействия для арок обычно несущественны. Вертикальные нагрузки относят к основным сочетаниям нагрузок, ветровые и температурные воздействия – к дополнительным, величина которых при определении расчетного усилия принимается с коэффициентом сочетания nc = 0,9.
Существенной нагрузкой для арочных конструкций является давление ветра. Ветровая нагрузка для арочных покрытий, не имеющих стен, принимается по упрощенной схеме.
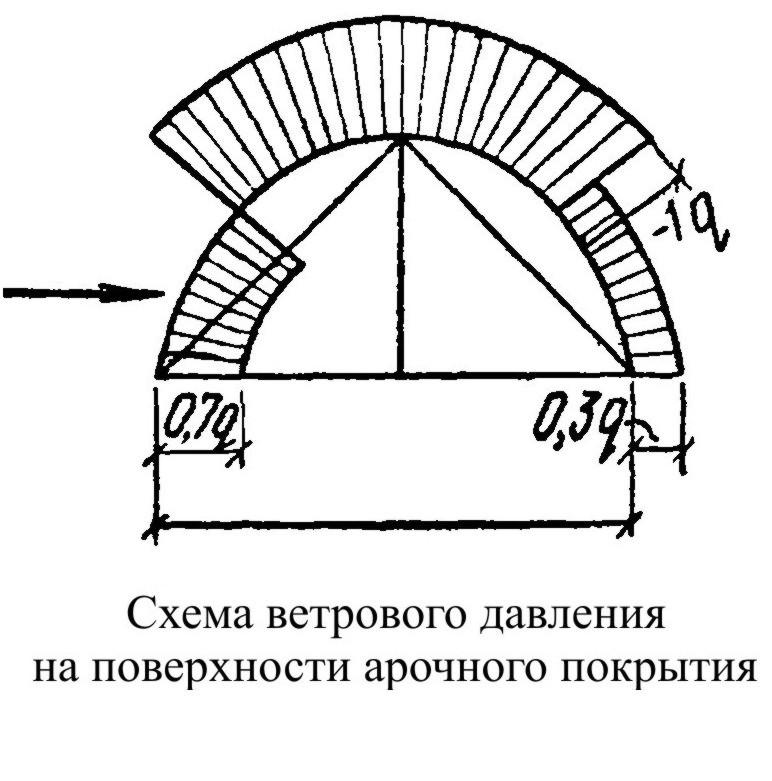
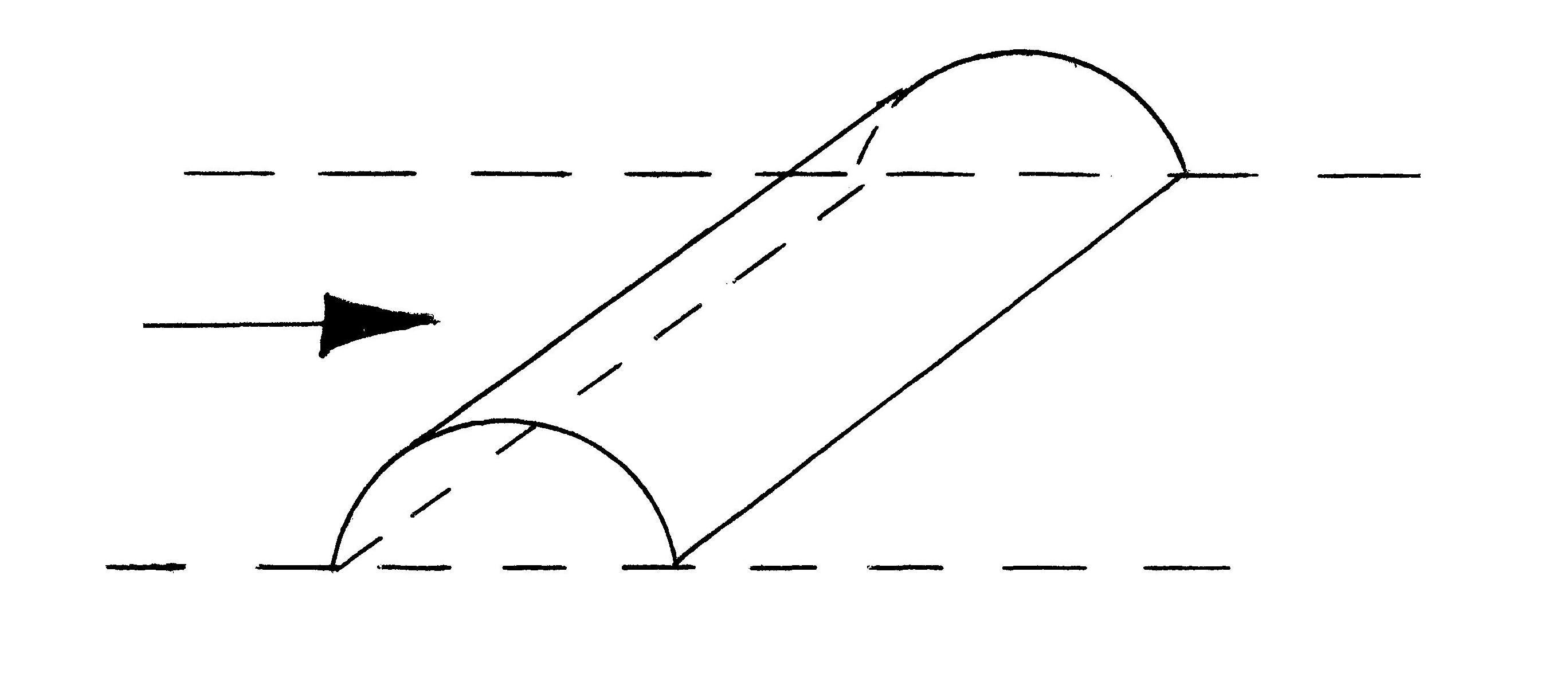
Ветровое давление считается приложенным нормально к поверхности арочного покрытия. Отрицательные ветровые усилия в высоких арках при малом собственном весе арки могут вызвать отрицательные опорные реакции.
На величину ветрового давления существенное влияние оказывают открытые проемы. При открытых торцах арочных покрытий ветер направленный параллельно торцам, обтекает сооружение с двух сторон, и внутри образуется вакуум, увеличивающий положительное давление на арки и уменьшающий отсос.
Для покрытий, торцы которых могут быть открытыми (навесы, вокзальные перекрытия и т.п.) необходимо учитывать возможные комбинации трех видов ветровых нагрузок:
-
бокового или торцового давления ветра на сооружение;
-
вакуума, создаваемого вследствие отсоса воздуха из-под арочного покрытия;
-
действия ветра внутри сооружения, который попадает под покрытие через широкие проемы и создает отрицательное давление.
Последние два вида нагрузок не нормированы и устанавливаются специальными техническими условиями для данного сооружения или на основе аэродинамических испытаний на моделях.
Конструкции арочных покрытий при расчете расчленяют на отдельные элементы (арки, прогоны и т.п.) и рассчитывают методами строительной механики (определяют M, Q, N).
Сечения стержней сквозных арок подбирают так же, как сечения стержней ферм. Арка как криволинейный сжатый брус требует проверки устойчивости.
Схема определения усилий в арке
При использовании арок в качестве перекрытий, они рассчитываются в общем случае на равномерно распределённую нагрузку (нагрузка от вышележащих конструкций перекрытий, снеговая нагрузка, нагрузка от собственного веса арки). В ходе расчета строятся эпюры усилий, возникающих в сечениях арки, по которым определяются наиболее опасные сечения. Формулы для определения усилий в каком-либо сечении арки следующие:
1. Изгибающий момент
,
где
Распор определяется из выражения:
,
где
2. Продольная сила
,
где
3. Поперечная сила
.
Литература
- Арка // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- АРКА — Термины на А, — терминология и типы арок.
- Арка — статья в Большой советской энциклопедии.
- Ю.М.Даниловский. МУ по расчету трехшарнирных арок – Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2004. — 21 с.
- Деревянные конструкции. Круговая и стрельчатая клееные арки. Конструирование и расчет: / Г.Н.Шмелёв.– Казань: Изд-тво Казанск. гос. архитект.-строит. ун-та, 2016. – 124 с.
- Манжосов, В. К. Расчет трехшарнирных арок : методические указания. – Ульяновск : УлГТУ, 2010. – 36 с.
- Арочные конструкции
- 2-х шарнирная рама с ригелем в виде клеефанерной балки
- Расчёт трёхшарнирной арки на статическую нагрузку
Схемы
арок, конструкция и расчет
Арки
относятся к распорным конструкциям, т.
е. для них характерно наличие горизонтальной
составляющей опорной реакции (распора).
Арки
используются в качестве основных несущих
конструкций зданий различного назначения.
Их применяют в покрытиях промышленных,
сельскохозяйственных и общественных
зданий пролетом от 12 до 70 м. В зарубежном
строительстве с успехом применяют арки
пролетом до 100 м и более.
По
статической схеме
арки разделяют на трехшарнирные и
двухшарнирные без ключевого шарнира:
Рисунок
8.1 – Трехшарнирная и двухшарнирная арки
По
схеме опирания
их делят на арки с затяжками, воспринимающими
распор, и на арки без затяжек, распор
которых передается на опоры.
Рисунок
8.2 – Арки без затяжки и с затяжкой
Затяжки
изготавливают в большинстве случаев
из арматуры или профильной стали.
Возможно применение деревянных клееных
затяжек, прежде всего в условиях химически
агрессивных сред. Дощатоклееные затяжки
повышают жесткость арок в процессе
транспортирования и монтажа, а также
предел огнестойкости.
По
форме оси арки делят на:
—
треугольные из прямых полуарок;
—
пятиугольные;
—
сегментные, оси полуарок которых
располагаются на общей окружности;
—
стрельчатые, состоящие из полуарок, оси
которых располагаются на двух окружностях,
смыкающихся в ключе под углом.
Рисунок
8.3 – Виды арок из прямолинейных элементов:
1
– трехшарнирная ломаного очертания с
опиранием на фундамент; 2 – трехшарнирная
треугольная переменного сечения с
опиранием на фундамент; 3 – трехшарнирная
треугольная постоянного сечения с
опиранием на фундамент
Рисунок
8.4 – Виды арок из криволинейных элементов:
1
– сегментная с металлической затяжкой;
2 – трехшарнирная кругового очертания;
3
– трехшарнирная кругового очертания,
переменного сечения; 4 – трехшарнирная
стрельчатого очертания; 5 – трехшарнирная
килевидного очертания; 6 – двухшарнирная
кругового очертания
По
конструкции арки делятся на:
1)
арки из полуарок цельного сечения
(только треугольной формы);
2)
арки из ферм;
Рисунок
8.5 – Арка из ферм (l=30…60
м, f=l/3…l/2)
3)
арки из балок на пластинчатых нагелях
(балок Деревягина);
4)
кружальные арки, состоящие из двух или
более рядов косяков, соединенных между
собой нагелями и имеющие смещенные
послойно стыки (могут быть кругового
или стрельчатого очертания);
Рисунок
8.6 – Кружальная арка:
а
– схема расположения косяков; б
– схема работы арки; в
– схема расчетных нагрузок
5)
арки с перекрестной дощатой стенкой на
гвоздях;
Рисунок
8.7 – Арка с перекрестной дощатой стенкой
(l=20…40
м, f≥l/6)
6)
клееные арки (дощатоклееные и клеефанерные).
Из
перечисленных видов арок наиболее
широкое применение получили клееные
арки заводского изготовления. Размеры
и несущая способность таких арок могут
отвечать требованиям сооружения покрытий
самого различного назначения, в том
числе уникальных по своим размерам.
Арки
остальных видов являются конструкциями
построечного изготовления и сейчас
практически не применяются. Дощатоклееные
деревянные арки представляют собой
пакет склеенных по пласти досок.
По
форме оси дощатоклееные арки могут
иметь любой из перечисленных выше видов,
т.е. они могут быть треугольными (без
затяжек – при высоте 1/2l
и с затяжками – при высоте 1/6 … 1/8l
в покрытиях до 24 м), пятиугольными с
гнутыми участками в местах переломов
осей, пологими сегментными двух- или
трехшарнирными со стрелой подъема не
менее 1/6l
(в редких случаях 1/7…1/8l)
и высокими трехшарнирными стрельчатыми
из элементов кругового очертания со
стрелой подъема 1/3…2/3l.
Последние два вида клееных арок
(сегментные и стрельчатые) рекомендуются
в качестве основных.
Поперечное
сечение клееных арок рекомендуется
принимать прямоугольным и постоянным
по всей длине. Высота поперечного сечения
назначается 1/30…1/50 пролета. Толщина
слоев для удобства гнутья принимается,
как правило, не более 1/300 радиуса кривизны
и не более 33 мм.
Клеефанерные
арки имеют перспективы применения в
легких покрытиях. Они, как правило, имеют
треугольную форму и состоят из коробчатых
клеефанерных полуарок. Такие арки имеют
малую массу и позволяют получать
существенную экономию древесины. Однако
они требуют расхода водостойкой фанеры,
являются более трудоемкими при
изготовлении, чем дощатоклееные и имеют
меньший предел огнестойкости.
Расчет
арок
Расчет
арок производится по правилам строительной
механики, причем распор пологих
двухшарнирных арок при стреле подъема
не более 1/4 пролета разрешается определять
в предположении наличия шарнира в ключе.
Расчет
арок после сбора нагрузок выполняется
в следующем порядке:
1)
геометрический расчет арки;
2)
статический расчет;
3)
подбор сечений и проверка напряжений;
4)
расчет узлов арки.
Нагрузки,
действующие на арку, могут быть
распределенными и сосредоточенными.
Постоянную равномерную нагрузку g
от веса покрытия и самой арки определяют
с учетом шага арок. Для арок криволинейного
очертания она обычно условно считается
(в запас прочности), равномерно
распределенной по длине пролета, для
чего ее фактическое значение умножают
на отношение длины арки к ее пролету
S/l.
Предварительное
определение нагрузки от собственного
веса проектируемой арки производится
по нижеприведенной формуле в зависимости
от ее типа, пролета, и величин нагрузок
от собственного веса покрытия gn,
снега p
и других нагрузок, например нагрузок
от подвесного транспортного оборудования
gсв
= (gn
+p
+ …)/[1000/(kcвl)
— 1]
Коэффициент
собственного веса kсв=2…4
при этом следует принимать в зависимости
от пролета и величин нагрузок на арку.
Снеговую
нагрузку р
определяют по приложению 3 СНиП
2.01.07.-85*
(схема 1 – для треугольных арок, 2 – для
арок кругового очертания, 2/
– для арок стрельчатого очертания).
Сосредоточенные,
временные нагрузки Р
включают в себя массу подвесного
оборудования и временных нагрузок на
нем.
Геометрический
расчет арки заключается в определении
всех размеров, координат сечений, углов
наклона касательных к оси в этих сечениях
и их тригонометрических функций,
необходимых для дальнейших расчетов.
Исходными данными при этом являются
пролет l,
высота f,
а в стрельчатых арках также радиус
полуарки r
или ее высота f.
По
этим данным в треугольных арках определяют
длину S/2
и угол наклона полуарки α.
В сегментных арках определяют радиус
r
= (l2
+4f)/8,
центральный
угол φ
из условия
и длину дуги
полуарки, и находят уравнение дуги в
координатах с центром в левой опоре
.
В
стрельчатых арках определяют угол
наклона α
и длину l
хорды, центральный угол φ
и длину S/2
полуарки, координаты центра a
и b,
угол наклона опорного радиуса φ0
и уравнение дуги левой полуарки
.
Затем половину пролета арки делят на
четное число, но не менее шести равных
частей и в этих сечениях определяют
координаты х
и у,
углы наклона касательных α
к горизонту и их тригонометрические
функции.
Статический
расчет
Опорные
реакции трехшарнирной арки состоят из
вертикальных и горизонтальных
составляющих. Вертикальные реакции Ra
и Rb
определяют как в однопролетной свободно
опертой балке из условия равенства нулю
моментов в опорных шарнирах. Горизонтальные
реакции (распор) Ha
и Hb
определяют из условия равенства нулю
моментов в коньковом шарнире.
Определение
реакций и усилий удобно производить в
сечениях только одной левой полуарки
в следующем порядке:
сначала
усилия от единичной нагрузки справа и
слева, затем от левостороннего,
правостороннего снега, ветра слева,
ветра справа и массы оборудования.
Изгибающие
моменты следует определять во всех
сечениях и иллюстрировать эпюрами.
Рисунок
8.8 – Геометрическая и расчетная схема
арки
Продольные
и поперечные силы можно определять
только в сечениях у шарниров, где они
достигают максимальных величин и
необходимы для расчетов узлов. Необходимо
также определять продольную силу в
месте действия максимального изгибающего
момента при таком же сочетании нагрузок.
Усилия
от двусторонней снеговой нагрузки и
собственного веса определяют путем
суммирования усилий от односторонних
нагрузок.
Полученные
результаты сводят в таблицу усилий, по
которой затем определяют максимальные
расчетные усилия при основных наиболее
невыгодных сочетаниях нагрузок.
Для
клееных арок «Пособие» к СНиП II-25-80
расчет на прочность рекомендует выполнять
при следующих сочетаниях нагрузок.
а)
в
пологих арках
(f<1/3l)
– расчетная
постоянная и временная (снеговая)
нагрузка на всем пролете и временная
нагрузка от подвесного оборудования;
– расчетная
постоянная нагрузка на всем пролете,
односторонняя временная (снеговая)
нагрузка на половине пролета и временная
нагрузка от подвесного оборудования;
– расчетная
постоянная нагрузка на всем пролете,
односторонняя временная (снеговая)
нагрузка, распределенная по треугольнику
на l/2,
и временная нагрузка от подвесного
оборудования;
б)
в стрельчатых арках (f≥1/3l)
—
расчетная постоянная и временная
(снеговая) нагрузки на всем пролете и
временная нагрузка от подвесного
оборудования;
—
расчетная постоянная нагрузка на всем
пролете, временная (снеговая) на S/2 или
части пролета в соответствии со СНиП
«Нагрузки и воздействия» и временная
нагрузка от подвесного оборудования;
—
ветровая нагрузка с постоянной и
остальными временными (с учетом
коэффициентов сочетаний: 0,9 – для
кратковременных нагрузок и 0,95 – для
длительных).
Максимальные
изгибающие моменты возникают обычно в
сечениях вблизи четверти пролета арки
при действии односторонних временных
нагрузок. В треугольных арках моменты
от вертикальных нагрузок уменьшаются
за счет обратных моментов М
от эксцентриситета е
продольных сил N.
Наибольшие
продольные силы возникают в сечениях
вблизи опор, а наибольшие поперечные
силы – в сечениях вблизи шарниров.
Усилия
в подвесках затяжек возникают от
подвешенных к ним грузов и от собственной
массы затяжек.
Подбор
сечений и проверка напряжений
производятся по максимальным значениям
расчетных усилий. При этом ветровые
нагрузки учитываются только в тех
случаях, если ветер более чем на 20 %
увеличивает расчетные усилия.
Арки
работают на сжатие с изгибом и
рассчитываются на прочность и устойчивость
в плоскости и из плоскости арки.
Подбор
сечений производится методом попыток
по величине изгибающего момента при
условно пониженном, например, до 0,8Ru
расчетном сопротивлении древесины
изгибу.
При
расчете арок выполняются следующие
проверки
1.
Проверка прочности по нормальным
напряжениям

2.
Расчет на устойчивость плоской формы
деформирования

3.
Проверка устойчивости в плоскости арки
выполняется по формуле
,
где
φ=f(λ)
– коэффициент продольного изгиба.
=l0/r.
Расчетную
длину элемента l0
следует принимать по пункту 6.25 СНиП
II-25-80
в зависимости от статической схемы и
схемы загружения арки.
При
расчете арки на прочность и устойчивость
плоской формы деформирования N
и Mg
следует принимать в сечении с максимальным
моментом (Mmax),
а расчет на устойчивость в плоскости
кривизны и определение коэффициента ξ
к моменту Mg
нужно определять, подставляя значения
сжимающей силы N0
в ключевом сечении арки.
Затяжки
и подвески арок работают и рассчитываются
на растяжение.
Узлы
арок
Основными
узловыми соединениями трехшарнирных
арок являются опорные и коньковые
шарниры.
Опорные
узлы арок без затяжек
выполняют, как правило, в виде лобовых
упоров в сочетании с металлическими
башмаками сварной листовой конструкции,
служащими для крепления их к опорам.
Рисунок
8.9 – Силовые воздействия в опорном узле
арки
Башмак
состоит из опорного листа с отверстиями
для анкерных болтов и двух вертикальных
фасонок с отверстиями для болтов
крепления полуарок.
Рисунок
8.10 – Опорный узел
Узлы
сегментных и стрельчатых арок, в которых
действуют изгибающие моменты разного
знака и незначительные поперечные силы,
центрируются по осям полуарок, а опорный
лист башмака перпендикулярен им.
Узлы
треугольных арок, в которых действуют
в основном положительные моменты и
значительные поперечные силы, центрируются
по расчетным осям, расположенным с
эксцентриситетом относительно осей
полуарок, а опорный башмак перпендикулярен
равнодействующей вертикальной и
горизонтальной опорных реакций.
Рисунок
8.11 – Опорная площадка, воспринимающая
опорную реакцию без сдвига
Расчет
опорного узла заключается в расчете
торца полуарки на смятие от действия
максимальной сжимающей силы Nсм.
В сегментных и стрельчатых арках она
равна максимальной продольной силе N
и действует вдоль волокон. В треугольных
арках она равна равнодействующей опорных
усилий
и
действует под углом к волокнам α,
определяемым из выражения
tg
=Q/N.
Рисунок
8.12 – Опорный узел с шарниром:
1
– опорная часть дощатоклееной арки; 2
– фундамент; 3
– стальной башмак;
4
– стяжные болты; 5
– цилиндрический шарнир; 6 – анкерные
болты
Болты
крепления фасонок к полуаркам рассчитывают
на действие максимальной поперечной
силы Q,
как симметрично изгибаемые, двухсрезные.
На эту же силу рассчитываются анкерные
болты на срез и смятие. Бетон фундамента
рассчитывается на смятие от силы Nсм.
Опорный
лист башмака работает на изгиб от
действия равномерного давления лобового
торца полуарки.
Опорные
узлы большепролетных арок без затяжек
выполняют с применением металлических
шарниров качающегося типа (рисунок
8.12).
Опорные
узлы клееных арок, работающих в условиях
химической агрессии, могут быть выполнены
при помощи стержней, одним концом
вклеенных в конец полуарки, а другим –
заанкерованных в фундамент.
Опорные
узлы арок с затяжками
Опорные
узлы клееных арок с затяжками выполняются
обычно при помощи лобового упора и
сварных металлических башмаков несколько
иной конструкции.
Опорный
лист в арках с затяжками располагается
горизонтально, поэтому арки ставятся
на горизонтальную поверхность опор, на
которые не действует распор. Вертикальные
фасонки могут опираться на опорный лист
или опорный лист может размещаться
между фасонками.
При
опирании на бетон опорный лист удлиняют
за пределы фасонок для крепления анкеров,
а при опирании на деревянную стойку,
фасонки опирают ниже опорного листа
для крепления их к стойке болтами. Между
фасонками располагается упорная
диафрагма. Наклон диафрагмы и центрирование
узла производятся по тем же соображениям,
что и в узлах арок без затяжек.
Металлическую
затяжку приваривают к фасонкам, деревянную
– располагают между фасонками и крепят
к ним болтами.
Рисунок
8.13 – Опорный узел с металлической
затяжкой:
а
– узел с лобовой передачей усилия сжатия
N
через торец арки; б
– узел с раздельным восприятием распора
и вертикальной опорной реакции
Рисунок
8.14 – Опорный узел с деревянной затяжкой:
1
– верхний пояс дощатоклееной арки; 2
– дощатоклееная стойка; 3
– деревянная затяжка;
4
– хомут из полосовой стали; 5
– стяжной болт с квадратной шайбой
При
расчете опорного узла следует выполнить:
1)
расчет диафрагмы на изгиб как балки,
заделанной в фасонках, на давление
лобового упора д;
2)
расчет опорного листа на изгиб как
двухконсольной или заделанной в фасонках
балки на реактивное давление фундаментов
б;
3)
определить длину сварных швов крепления
затяжки или число крепежных болтов –
для деревянных затяжек из условия
восприятия ими усилия в затяжке.
Опорные
узлы дощатых арок с затяжками выполняется
при помощи гвоздевых или болтовых
соединений досок пояса и затяжки.
Затяжки
брусчатых арок из арматурной стали
пропускаются через отверстия в конце
полуарки и закрепляются гайками с
шайбами.
Расчет
таких узлов производят на смятие торцевых
обрезов.
Рисунок
8.15 – Опорный узел арки:
1
– верхний криволинейный пояс дощатоклееной
арки; 2
– затяжка из круглой стали;
3
– стальная листовая подкладка переменной
жесткости; 4
– стальные накладки; 5
– опора
Коньковые
узлы сплошных арок малых и средних
пролетов решаются в виде прямых или
наклонных лобовых упоров со стальными
креплениями или деревянными накладками
на болтах. Сегментные и стрельчатые
клееные арки центрируются в этих узлах
по осям полуарок, а треугольные – с
эксцентриситетами (с той же целью, что
и в опорных узлах).
Лобовые
упоры конькового узла рассчитывают на
смятие под углом или вдоль волокон на
действие продольной силы N.
Количество болтов в стальных креплениях
определяется в зависимости от величины
поперечной силы Q
с учетом угла смятия древесины под
болтами. Монтажные болты рассчитывают
на срез и смятие от действия той же силы
Q.
Рисунок
8.16 – Коньковый узел треугольной арки
Рисунок
8.17 – Коньковый узел сегментной арки
Коньковые
узлы большепролетных арок выполняются
в виде стальных шарниров качающегося
типа.
Рисунок
8.18 – Стальной шарнир качающегося типа
1
– верхняя часть полуарки; 2
– боковые накладки стальных сварных
башмаков;
3
– болт валикового шарнира; 4
– проушины башмака; 5
– ребра жесткости башмака; 6
– стальные болты с гайками; 7
– стальные нагели
Стыки
элементов арок.
Стыки
клееных арок представляют собой зубчатые
соединения досок по длине и стыки по
пласти слоев досок между собой (в арках
шириной сечения более 180 мм могут
применяться еще и стыки по кромкам).
Арки больших пролетов соединяются по
длине жесткими стыками с помощью
двусторонних накладок из профильной
стали и болтов.
Трехшарнирная арка
- Определение опорных реакций в арке.
Арку решают совместно с балкой. То, что относится к арке, обозначается просто, а то, что к балке – с индексом «0».
Балку берут того же пролета и той же нагрузки. А в балке возникают только вертикальные реакции.
Определим вертикальные реакции для арки:
Для балки результат такой же. Вертикальные реакции и в балке, и в арке одинаковые.
Чтобы определить горизонтальные реакции, проецируем все силы на ось Х.
Чтобы найти распор, воспользуемся известным свойством шарнира С.
Составим уравнение
Теперь сносим сечение С на балку (шарнир сносить нельзя, балка будет мгновенно изменяема). Ищем момент относительно сечения С.

Сравним с формулой НА. Тогда:
Т.о. распор (и усилие в затяжке при ее наличии) обратно пропорционален стреле подъема арки.
- Определение внутренних силовых факторов в арке.
Делаем в арке сечение 1-1 и определяем в нем М1. Если в балке менялось расстояние по горизонтали, то в арке меняется и по вертикали – по оси у.
Спускаем сечение 1-1 на балку и определяем момент в этой точке.
Сравниваем формулы и получаем формулу для определения изгибающего момента М в арке:
В арке изгибающий момент меньше, чем в балке — арка экономичнее по материалу.
Формула для определения продольной силы N:
Формула для определения поперечной силы Q:
Для расчета арок требуется знать уравнение криволинейной оси арки. Оно зависит от ее очертания. Уравнения криволинейных осей арок смотреть — здесь.
|
Собираемся сделать арку между гостиной и детской комнатами — муж хочет сам произвести расчеты, посоветуйте, как это сделать? Рассчет арки, а точнее ее изгиба, вопрос вкуса, главное рассчитать центральную точку и отталкиваясь от нее ровно вырезать полукруг. Для этого потребуется измерить ширину и высоту арки, а также определиться с высотой закругления. Стоит учитывать, что закругление не должно сильно возвышаться над дверями (если таковые имеются в одном помещении с аркой), так как арка будет казаться слишком высокой. Если Вам необходим идеальный полукруг, то можно в центральную точку закрутить саморез, а далее при помощи веревочки/ниточки и карандаша,очертить полукруг. Иначе, понадобится какая-нибудь гибкая планка, например, порожек или что-то подобное, главное, чтобы он легко гнулся, но при этом сохранял форму за счет своей упругости. Прикладываем, изгибаем и прочерчиваем. Вырезаем при помощи ножа или электролобзика. Вот и все, шаблон готов. система выбрала этот ответ лучшим домовой 7 лет назад Что вы имели ввиду под расчётом арки непонятно, но скорее всего имели ввиду рассчитать какой сделать изгиб, это дело лично каждого и его удобства, но изгиб не должен мешать удобному и беспрепятсвенному проходу людей, если вы занизите края арки то, проход будет возможен только в средней части проёма, а это уже решать вам устраивает вас это или нет — возможно устраивает. Поэтому вначале нужно определится на какой высоте проёма будут находится края арки и отметить их на стенах или проёме, допустим это высота 1.70 метра, вот вам и первый расчёт. Далее нужно определить центр проёма на высоте и уже от него делать изгиб самой арки, в каждом случае он получится разный в зависимости от самой высоты и ширины проёма, в любом случае вы можете только регулировать высоту краёв изменяя угол окружности, больше ничего. Пусть возьмут пластиковую панель, она достаточно легко гнётся и просто методом подбора, найдут оптимальный вариант, ничего сложного в расчёте арки нет, тем более декоративной, это не свод моста, тут учёным быть не нужно! Вот некоторые размеры и расчёты арок. Ким Чен Ын 6 лет назад Арки сами по себе разные, не только по типу конструкции, но и по материалу изготовления. Методы расчётов так же не одинаковые, можно пойти математическим путём и рассчитать арку с использованием математических формул, можно всё сделать гораздо проще, то есть абсолютно практические расчёты. Измеряем дверной проём где будет арка (длина, ширина, высота). Переносим все размеры на лист бумаги, но сразу же определяемся с точным масштабом, то есть на бумаге должен быть выдержанный в определённом масштабе чертеж. Чертим проём (см. выше о масштабе). Делим его строго пополам, линией, по ширине и длине. В этой точке ставим ножку циркуля и чертим дугу, если дуга не понравилась (другой радиус интересует) можно начертить несколько дуг и остановиться на понравившейся, остальные стереть ластиком. Всё, арка готова, осталось перенести размеры в реальном масштабе, сделать шаблон и так далее. Можно воспользоваться и специальными программами расчёта арок. Вам в помощь будет простейшая геометрическая формула, в которой вы исходя из высоты предполагаемой дуги (на картинке под обозначением h) и длины хорды, а по сути ширины пролёта без отделки (на картинке под обозначением a), высчитываете радиус (на картинке под обозначением R) и если нужно, то длину хорды (на картинке под обозначением b). Можно пойти от обратного, если у вас есть готовая арка и вам нужно рассчитать какой проём нужно вырезать, то получается от радиуса арки и высоты дуги вы можете высчитать ширину проёма и гипотенузу. Для этой цели можно воспользоваться программой «PowerArch», она хоть и платная, но есть ознакомительная версия, которой вам хватит для расчёта одной арки. очУмелый Фламинго 8 лет назад При расчете каждой детали для арки, делайте их немного больше, чем по чертежу, так как детали будут накладываться друг на друга, стыковаться. Среднестатистическая ориентировка на высоту арки — 10 процентов ширины двери над ее проемом. Радиус арки удобнее рассчитать при помощи школьной формулы: R = (L+H) / 2H. Н – высота арки от точки L. L – центр ширины, расстояние до центра ширины арки от края к середине, точка L делит всю ширину ровно пополам. R – радиус арки. Сначала измеряется ширина будущей арки, этот показатель делят пополам, центр будет точкой отсчета, обозначенный буквой L. Высота арки и радиус не всегда совпадают, поэтому их определяют по отдельности, высоту можно сразу вычислить, если соединить центр ширины и максимально высокую точку, а радиус находят по заданной формуле. Прежде, чем делать арку из дерева и досок, следует изготовить шаблон из картона или бумаги, чтобы быть уверенным в правильности проведенных расчетов. Можно делать арку без расчетов, подбирать высоту на свое усмотрение, но тогда следует добавить 5 сантиметров для проема арки, который будет накладывать поверх дверного проема для фиксации. Знаете ответ? |