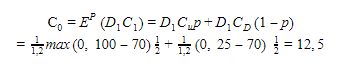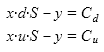Как найти стоимость опциона

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Категории стоимости опциона

Финансисты, говоря об опционной доходности, оперируют понятиями цена или стоимость, которые являются премией, выплачиваемой один раз. Данную денежную сумму покупатель отдает продавцу в момент заключения сделки.

Стоимость имеет две категории: внутреннюю и временную. Формула расчета выглядит так:

Po = Io + To,

где:

Po – это цена (премия);

Io – внутренняя стоимость;

To – временная стоимость.

Премия по выигрышному опциону складывается из сумм внутренней и временной стоимостей. Премия по проигрышному контракту – это отражение временной стоимости, так как внутренняя в таком случае равна нулю.

Io (внутренняя)

Внутренней стоимостью опциона называют показатель суммы выручки, которую получил бы владелец договора при условии неизменности цены на него. Параметр равен дельте (соотношению) между страйковой (цена исполнения) и спотовой (цена актива, на который опирается опцион) ценами.

Внутренняя стоимость подчиняется определенным правилам:

• величина всегда положительная или равная нулю. Соглашения с плюсовой внутренней стоимостью находятся в позиции «в деньгах», договоры с нулевой стоимостью относятся к группе «около денег»;
• параметр характеризуется постоянностью, не изменяясь на протяжении реализации опциона.

Формула:

Io = Po – To

Пример расчета:

Цена акции фирмы Z – 400 тысяч рублей. Инвестор Х удерживает опцион колл, купив контракт за 200 тысяч рублей. При продаже опциона в настоящий момент:

• покупка актива – 200 тысяч рублей;
• продажа – 400 тысяч рублей;
• получена прибыль в размере 200 тысяч рублей.

Торгуется put опцион в 300 тысяч рублей. Сначала продается актив по цене договора, затем выкупается инвестором обратно по спотовой стоимости. В этом случае внутренняя стоимость будет равна 100 тысяч рублей.

To (временная)

Под временной стоимостью понимают возможность, выраженную в денежной сумме, предоставляемую опционом за определенный временной промежуток. Расчет выполняется по формуле:

To = Po – Io

По мере приближения к завершению сделки цена стремится вниз даже при нахождении внутренней стоимости в неизменном виде.

Постоянное падение временной цены привело к необходимости использовать модель для расчета стоимости договора на определенное число. На современном этапе для этого есть множество формул, однако наиболее широко используются две: ВОРМ (биноминальная модель ценообразования) и Блэка-Шоулза.

Временная стоимость зависит от:

• длины временного отрезка до момента исполнения обязательств. Вероятность повышается с увеличением времени до даты окончания опциона;
• изменчивости спот цены. Высокий уровень изменчивости увеличивает вероятность большого рывка цены базового актива;
• процентных ставок. Данный показатель меньше всего оказывает влияние на опцион. Это происходит при большом объеме контракта.

Необходимо, чтобы временная стоимость учитывала риски для продавца и преимущества владения договором для покупателя.

Пример:

Соглашение в 210 долларов (колл). Базисный актив стоит 203 доллара. Разница составляет 7 долларов – это и есть временная стоимость (премия за время).

Аналитика соотношения внутренней и временной стоимости представляет собой теоретическую выкладку. Обычно анализ имеет вид графика, из которого видна динамика изменения с течением времени. Именно он наглядно демонстрирует истечение временной стоимости, уменьшающейся с приближением даты исполнения контракта. В процессе аналитики необходимо учитывать то, как одни параметры своими изменениями влияют на другие.

Внутренняя и временная стоимости имеют большое значение для биржевой торговли. Их свойства лежат в основе разных стратегий, направленных на извлечение преимуществ от различных опционных характеристик.

×

Политика конфиденциальности АО ИК «ЦЕРИХ Кэпитал Менеджмент»

Настоящая политика конфиденциальности АО ИК «ЦЕРИХ Кэпитал Менеджмент» (далее — Политика) разработана в соответствии с Федеральным законом от 27.07.2006 N 152-ФЗ «О персональных данных» и устанавливает правила использования АО ИК «ЦЕРИХ Кэпитал Менеджмент» (далее – Компания) персональной информации, получаемой от пользователей сайта www.zerich.com (далее — сайт), интернет-сервисов и мобильных приложений Компании.

Получение доступа к использованию сайта, интернет-сервисов и мобильных приложений Компании означает безоговорочное согласие Пользователя с положениями настоящей Политики и указанными в ней условиями обработки Компанией персональной информации пользователя.

Под интернет – сервисами и мобильными приложениями для целей применения настоящей политики подразумеваются любое программное обеспечение, позволяющее осуществлять электронное взаимодействие между пользователем и Компанией в процессе заключения/исполнения/расторжения соглашений на финансовом рынке, а также предоставления Компанией информации о своих услугах.

Компания собирает, обрабатывает и использует в определенных настоящей Политикой целях:

— персональную информацию пользователя, которую пользователь самостоятельно предоставляет Компании при переходе на сайт, создании учетной записи/регистрации/авторизации на сайте, в мобильном приложении Компании, в интернет — сервисах Компании, в том числе: фамилия, имя, отчество, пол, возраст, дата рождения, место рождения, адрес электронной почты, номер мобильного телефона, ссылки на профили в социальных сетях, реквизиты банковской карты;

— а также иные пользовательские данные, автоматически передаваемые Компании в процессе использования сайта, мобильного приложения, интернет-сервисов Компании: IP-адрес; версия ОС; версия веб-браузера; сведения об устройстве (тип, производитель, модель); разрешение экрана и количество цветов экрана; версия Flash; версия Silverlight; наличие программного обеспечения для блокирования рекламы, наличие Cookies, наличие JavaScript; язык ОС и Браузера; время, проведенное на сайте; действия пользователя на сайте), версия операционной системы мобильного устройства, с которого осуществляется доступ к мобильным приложениям Компании, данные об активности пользователя в сети Интернет, о посещенных пользователем страницах, дате и времени URL-переходов, файлы cookies.

Персональная информация пользователя обрабатывается Компанией в целях:

— установления и поддержания связи и документооборота с пользователем,

— регистрации пользователя на сайте Компании, управление учетной записью пользователя,

— предоставления пользователю доступа к мобильному приложению и иным сервисам Компании,

— принятия Компанией решения о приеме пользователя на обслуживании е в Компанию,

— исполнения Компанией обязательств перед пользователем по соглашениям между пользователем и Компанией,

— улучшения качества обслуживания пользователя,

— исполнение требований законодательства Российской Федерации,

— исполнения обязательств Компании перед контрагентами и государственными органами,

— технического управления мобильным приложением и интернет-сервисами Компании, улучшения их работы,

— выявления, пресечения недобросовестных действий третьих лиц, а также устранения технических сбоев или проблем безопасности;

— защиты прав Компании, клиентов Компании способами, соответствующими законодательству Российской Федерации,

— предоставление пользователю информации об услугах и продуктах Компании и ее партнеров,

— проведения маркетинговых мероприятий,

— статистических и иных исследований,

— в иных целях, предусмотренных заключенными между Компанией и пользователем соглашениями.

Компания вправе предоставлять информацию пользователей аффилированным лицам Компании и контрагентам Компании в вышеуказанных целях. При этом аффилированные лица Компании, а также контрагенты Компании должны соблюдать требования сохранения конфиденциальности обрабатываемой информации пользователей.

В целях исполнения требований законодательства Российской Федерации Компания вправе предоставлять информацию пользователей уполномоченным государственным органам на основании соответствующих письменных запросов.

Компания гарантирует, что персональная информация пользователей не разглашается, а также не предоставляется Компанией иным лицам, за исключением случаев, прямо предусмотренных в настоящей Политике.

Предоставление персональной информации пользователей третьим лицам, по основаниям, не указанным в настоящей Политике, допускается только при наличии дополнительного согласия пользователя, которое может отозвано пользователем в любое время.

Сайт, мобильное приложение, интернет-сервисы Компании не являются общедоступными источниками персональных данных.

Компания принимает все необходимые и достаточные правовые, организационные и технические меры для защиты информации, предоставляемой пользователями от неправомерного или случайного доступа, уничтожения, изменения, блокирования, копирования, распространения, а также от иных видов неправомерного использования и неправомерных действий третьих лиц.

Компания ограничивает доступ сотрудников Компании, ее аффилированных лиц, а также контрагентов к персональной информации пользователей, которая не является необходимой для исполнения требований законодательства Российской Федерации либо выполнения существующих обязательств перед пользователями либо достижения иных целей, указанных в настоящей Политике.

Трудовые договоры с сотрудниками Компании, а также с контрагентами Компании предусматривают меры ответственности и штрафные санкции за нарушение конфиденциальности персональной информации пользователей.

Компания рекомендует пользователям соблюдать конфиденциальность данных учетных записей, логинов, паролей для доступа к мобильным приложениям и сервисам Компании. Пользователь обязуется незамедлительно сообщать Компании о любом случае компрометации паролей, логинов для доступа к мобильным приложениям и сервисам Компании, используемых ключей электронной подписи, а также выявленного пользователем несанкционированного использования его учетной записи. Соблюдение пользователем настоящей рекомендации позволит обеспечить максимальную сохранность предоставленной Компании информации.

Компания оставляет за собой право в любое время вносить изменения в настоящую Политику.

Новая редакция Политики вступает в силу с момента ее размещения на сайте. Продолжение пользования сайтом, мобильным приложением, интернет-сервисами Компании после публикации новой редакции Политики на сайте Компании означает безусловное согласие пользователя с новой редакцией Политики.

На пользователе лежит обязанность знакомиться с текстом Политики при каждом посещении сайта, мобильного приложения или интернет-сервисов Компании.

Вы могли бы успешно победить рынок, торгуя акциями, используя дисциплинированный процесс, ожидая хорошего движения вверх или вниз. Многие трейдеры также обрели уверенность в том, что могут зарабатывать деньги на фондовом рынке, определяя одну или две хорошие акции, которые вскоре сделают большой шаг вперед. Но если вы не знаете, как воспользоваться этим движением, вы можете остаться в пыли. Если это похоже на вас, возможно, пришло время подумать об использовании опций.

В этой статье будут рассмотрены факторы, которые следует учитывать, если вы планируете торговать опционами, чтобы воспользоваться движением акций. Опционы — это контракты с производными финансовыми инструментами, которые дают держателю право, но не обязательство, купить (в случае колл) или продать (в случае пут) базовый актив или ценную бумагу по заранее определенной цене (называемой цена исполнения ) до истечения срока действия контракта. Это право связано с ценой, называемой премией за опцион. Понимание того, как оценивать эту премию, имеет решающее значение для торговли опционами и, по сути, основывается на вероятности того, что право на покупку или продажу в конечном итоге окажется прибыльным по истечении срока действия.

Модели ценообразования опционов

Прежде время до истечения срока или временная стоимость, волатильность, процентные ставки и выплаченные денежные дивиденды.

Существует несколько моделей ценообразования опционов, в которых эти параметры используются для определения справедливой рыночной стоимости опциона.Из нихнаиболее широко известна модель Блэка-Шоулза. Во многих отношениях опционы ничем не отличаются от любых других инвестиций — вам нужно понимать, что определяет их цену, чтобы использовать их эффективно. Также широко используются другие модели, такие как биномиальная модель и трехчленная модель.

Начнем с основных факторов, влияющих на цену опциона: текущая цена акций, внутренняя стоимость, время до истечения срока или временная стоимость и волатильность. Текущая цена акций довольно проста. Движение цены акции вверх или вниз имеет прямое, хотя и не равное, влияние на цену опциона. По мере того, как цена акции растет, более вероятно, что цена опциона колл вырастет, а цена опциона пут упадет. Если цена акций упадет, с ценой колл и пут, скорее всего, произойдет обратное.

Формула Блэка-Шоулза

Модель Блэка-Шоулза, пожалуй, самый известный метод ценообразования опционов. Формула модели получается путем умножения цены акции на кумулятивную функцию стандартного нормального распределения вероятностей. После этого чистая приведенная стоимость (ЧПС) страйковой цены, умноженная на кумулятивное стандартное нормальное распределение, вычитается из результирующего значения предыдущего расчета.

В математической записи:

Математика, связанная с дифференциальным уравнением, составляющим формулу Блэка-Шоулза, может быть сложной и пугающей. К счастью, вам не нужно знать или даже понимать математику, чтобы использовать моделирование Блэка-Шоулза в ваших собственных стратегиях. Торговцы опционами и инвесторы имеют доступ к множеству онлайн-калькуляторов опционов, и многие из сегодняшних торговых платформ могут похвастаться надежными инструментами анализа опционов, включая индикаторы и электронные таблицы, которые выполняют вычисления и выводят значения цен опционов.

Ниже мы немного углубимся в цены опционов, чтобы понять, что составляет их внутреннюю и внешнюю (временную) стоимость, что немного проще.

1:23

Внутренняя стоимость

Внутренняя стоимость — это стоимость любого опциона, если бы он был исполнен сегодня. По сути, внутренняя стоимость — это сумма, на которую цена исполнения опциона является прибыльной или в деньгах по сравнению с ценой акции на рынке. Если цена исполнения опциона невыгодна по сравнению с ценой акции, то считается, что опцион не при деньгах. Если цена исполнения равна цене акции на рынке, опцион считается «при деньгах».

Хотя внутренняя стоимость включает соотношение между страйк-ценой и ценой акции на рынке, она не учитывает, сколько (или как мало) времени осталось до истечения срока действия опциона, называемого истечением. Время, оставшееся до исполнения опциона, влияет на премию или стоимость опциона, что мы рассмотрим в следующем разделе. Другими словами, внутренняя стоимость — это часть цены опциона, которая не теряется или не подвергается влиянию с течением времени.

Одной из самых сложных вещей для понимания в финансах является формирование цены опциона. Основная сложность здесь — это ее нелинейность, нет постоянной корреляции цены опциона и цены базового актива. 

Обычно для расчета цены опциона используется формула Блэка-Шоулза, метод Монте-Карло и подобные. Мы не будем разбирать эти формулы, а рассмотрим на бытовом уровне факторы, которые оказывают прямое влияние на цену опциона.

Временная стоимость опциона.

Временную стоимость опциона можно сравнить с ценой обычной страховки. Чем больше срок и шире покрытие такой страховки, тем выше ее стоимость. Тот же принцип и на рынке опционов: опцион с ценой исполнения близкой к текущей цене базового актива и с истечением через несколько месяцев будет стоить дороже чем «дальний» опцион с датой экспирации через 3 дня.

Временная стоимость теряется очень неравномерно: потеря временной стоимости в процентах будет ускоряться с течением времени и в последние дни «жизни» стоимость опциона будет снижаться ежедневно на десятки процентов, стремясь к нулю.

Еще одним фактором, который влияет на временную стоимость — это насколько далеко текущая цена базового актива будет находиться от страйка (от цены исполнения опциона). Чем глубже опцион будет «в деньгах» (цена базового актива перешла через страйк) или «вне денег», тем ниже будет доля временной стоимости в общей стоимости опциона.

Внутренняя стоимость опциона.

Именно за счет внутренней стоимости опцион может дорожать на сотни и дешеветь на десятки процентов в течение одной торговой сессии. Внутреннюю стоимость опциона можно достаточно легко просчитать — это разница между ценой исполения и текущей ценой базового актива. Рассмотрим на примере.

Допустим, опцион Call имеет цену исполнения (страйк) 10 000 пунктов (здесь для примера не важна валюта). Базовый актив вырос с 9 500 до 11 000. Цена 9500 была ниже цены страйк (10 000), поэтому опцион Call имел внутреннюю цену равную нулю. При 11 000 наш опцион «зашел в деньги» на 1000 пунктов, значит его внутренняя стоимость равна 1000. То есть, при цене базового актива 9500 наш опцион нет смысла исполнять по 10 000 — мы получили бы убыток 500 пунктов на каждый опцион, а также лишились бы и самого опциона, который оценивался по меньшей мере по временной стоимости. При цене выше 10 000 мы можем как продать опцион по рыночной цене, так и исполнить его и получить доход.

Аналогично считается внутренняя стоимость опционов Put, только нужно проводить обратное действие — из цены страйк вычитать текущую цену базового актива. Например, если страйк опциона Put равен 10 000, а текущая цена базового актива 9 500, то опцион будет иметь внутреннюю стоимость 500. При цене базового актива выше 10 000 исполнение опциона экономически не целесообразно.

В редких случаях трейдеры могут намеренно исполнять опционы «вне денег», например, если текущая ликвидность инструмента не позволяет купить или продать необходимый объем без существенного его изменения цены. Скажем, покупка большого объема инструмента по рыночной цене приведет к тому, что средняя цена покупки будет на несколько процентов отличаться от текущих цен. Альтернатива — купить недорогие опционы с ближайшей датой экспирации и ближайшим страйком и исполнив их получить на брокерский счет базовый актив.

Волатильность и оценка стоимости опциона.

Волатильность оказывает сильное влияние на временную стоимость опционов. Сильные движения цены часто приводят и к большим коррекциям, что значительно повышает шансы того, что цена дойдет даже до дальних страйков. Поэтому при сильных колебаниях рынка временная стоимость опционов может увеличиться в разы, что может быть неприятным сюрпризом для продавцов опционов.

Получить практический опыт работы с опционами можно на наших онлайн курсах. Остались вопросы? Обсудите их с нашими специалистами по бесплатному номеру 8 (800) 775-11-99

Это третья часть рассказа про опционы, где мы поговорим про биномиальную модель, риск-нейтральную меру и разберёмся, как рассчитать цену опциона.

Если вы пропустили наш подробный рассказ про опционы, вот ссылки на предыдущие части:
— Что такое опционы и кому это нужно. Ликбез для гика, ч. 6
— Опционы: пут-колл парити, броуновское движение. Ликбез для гика, ч. 7

Данный пост основан на расшифровке моих видеолекций «Одношаговая биномиальная модель» и «Расчет опциона», созданных в рамках курса Finmath for Fintech.

Одношаговая биномиальная модель. Можно ли считать цену опциона как математическое ожидание дисконтируемой выплаты? Что может пойти не так?

Следующее понятие, которое необходимо обсудить, — риск-нейтральная мера. Это понятие в общем виде требует не-школьной математики, поэтому, как и ранее, мы не будем что-то доказывать в общем виде. Вместо этого начнем с очень простого примера (даже может показаться, что он слишком простой и вообще не имеет никакого отношения к реальным моделям для нашей темы). На этом примере мы увидим, как работают термины, а все результаты, которые мы получим, будут верны и в более общем случае. 

Мы рассматриваем биномиальную модель с дискретным временем. У нас есть два момента времени, в которых наблюдается рынок: t₀ и t₁, есть некий рисковый актив, т.е. он содержит в себе риск. Его цена в момент t₀ равна 50. И есть два варианта развития события в будущем (поэтому модель и называется биномиальной): цена может увеличиться до 100 или упасть до 25. Это наш рисковый актив, в котором есть некоторая неопределенность. Также нам в нашей модели нужен некоторый безрисковый актив, аналог банковского счета в надёжном банке. Предположим, у нас риск-нейтральная ставка 20% и, значит, деньги, положенные в момент времени t₀ на депозит в количестве 50 в момент времени t₁ дадут выплату 60.

В нашей модели есть некоторые вероятности. Обозначим их: p — вероятность того, что актив увеличится в цене, и вероятность того, что актив в цене уменьшится: 1-p.

Если бы мы работали с активом, в котором нет никакой неопределенности, то цена такого актива в момент времени t₀ была бы просто дисконтированной выплатой в момент t₁, как это есть для безрискового актива. Но у нас есть два варианта с некоторой неопределенностью. Логично выглядит предположение о том, что, используя эти вероятности, мы бы могли просчитать математическое ожидание от дисконтированной выплаты какого-то производного продукта. Если мы рассмотрим колл-опцион на такой риск базовый актив, то его цена, наверное, будет равна математическому ожиданию дисконтированной выплаты в момент времени t₁:

Это наше предположение.

Тут D₁ — коэффициент дисконтирования из момента t₁ в момент t₀. Посчитаем, чему будет равно записанное выше выражение. Для определенности давайте скажем, что страйк этого опциона K равен 70. Тогда у нас есть все данные, чтобы посчитать мат. ожидание.

Проверим, работает ли наше предположение. Мы сделаем так: составим некоторый портфель из опциона, базового актива в момент t₀ и рассмотрим его выплату в момент t₁. Составим портфель следующим образом. Мы продаем 15 колл-опционов и покупаем 6 штук базового актива. Берем в долг 125 единиц денег. Такие вот магические цифры, чуть попозже мы увидим, откуда они берутся, как их можно посчитать, но пока это просто выбранные константы. В момент времени t₀ изменение нашего баланса будет выглядеть следующим образом:

Мы получаем прибыль за 15 опционов: +15С₀; платим за шесть единиц базового актива по цене 50:  -6*50; получаем: +125 денег.

Далее следует момент времени t₁ и два возможных варианта: когда цена актива (S₁) стала 25 и когда цена актива стала 100. В первом случае, когда цена стала 25 при страйке 70, опцион ничего не стоит. Когда цена стала 100, и мы продали 15 опционов, нам нужно заплатить премию -15*(100-70). Приобретенные шесть единиц базового актива у нас на балансе, мы можем их продать и получить деньги по текущему курсу 6*25 или 6*100 соответственно тому, какая цена реализовалась. Наш долг увеличивается согласно процентной ставке, и мы получаем выплату, в обоих случаях одинаковую, которая не зависит от цены актива: -150. Теперь сложим все числа, которые у нас получились на момент времени t_1. Как видим, в обеих колонках получаем ноль. Это связано с тем, что изначально цифры были специально подобраны. 

В момент времени t₁ независимо от того, какой сценарий реализуется, портфель, составленный таким образом, стоит ноль. Следовательно, в момент времени t₀ он тоже должен стоить столько же — ноль. Мы опять используем условие отсутствие арбитража на рынке. 

Приравняв эту сумму к нулю, мы получаем цену опциона:

Мы видим, что результат 11,6 не совпадает с тем, что получили ранее: 12,5. Этот, казалось бы, интуитивно верный результат не сработал. Составив специальный портфель, мы увидели, что, если бы цена на колл-опцион была 12,5, это бы как раз и означало наличие арбитража на рынке. То есть при такой цене на колл-опцион можно было бы зарабатывать деньги без риска. Давайте разберемся, почему же так получилось.

Одношаговая биномиальная модель. Расчет опциона. Риск-нейтральные вероятности

Чтобы проанализировать полученный результат, давайте немного обобщим модель и будем работать уже не с фиксированными числами, а с какими-то параметрами. Обозначим текущий курс рискового актива как S, введем параметр d и параметр u. У нас к моменту времени цена t₁ рискового актива может пойти либо вниз в d раз, либо вверх в u относительно текущего уровня. Цена безрискового актива по-прежнему определяется некоторым дискаунт-фактором. 

Заметим, что по построению параметры модели заданы так, что d<D₁^-1<u (см. рис. 4).

По поводу составления портфеля следует заметить, что мы сразу можем поделить весь портфель на номинал нашей позиции в опционах. Это, возможно, даст нам дробные номиналы в каких-то других позициях, но мы разрешаем себе с этим работать в рамках нашего математического анализа. Мы будем работать с любыми действительными числами — как с положительными, так и с отрицательными. В рамках практики рынка отрицательные позиции соответствуют short selling, и могут быть определенные ограничения на такие позиции, но мы этим в нашем тоже анализе пренебрегаем. 

Так как мы можем поделить все на номинал нашей позиции в опционах, то мы просто будем рассматривать один опцион. И для составления портфеля остается только два параметра: размеры позиций в рисковом и безрисковом активах.

Купим какое-то количество x базового актива S и возьмем в долг какое-то количество денег, такое, чтобы получить выплату ровно y. Мы его дисконтируем на момент t₀ и получаем D₁y. Мы берем в долг D₁y, а выплатить в момент t₁ нам нужно будет y. Т.е. для баланса это будет сумма -y.

В случае с базовым активом мы покупаем на сумму — xS. У нас возможны два случая: когда цена пошла вниз S₁=d*S и когда цена пошла вверх S₁=u*S. Соответственно, наша позиция будет стоить x*d*S или  x*u*S. И мы продаем один колл-опцион, в начальный момент времени мы за него получаем премию C₀. В момент времени t₁ мы обязаны сделать выплату по этому опциону, так как взяли на себя это обязательство: —C_d и -C_u соответственно.

Выплата в момент времени t₁ определяется также еще одним параметром — страйком опциона, это некоторое заданное число. Как и в прошлый раз, мы бы хотели построить портфель таким образом, чтобы в обоих случаях, вне зависимости от того, какая цена базового актива реализовалась, в конце портфель бы стоил ровно ноль. Давайте посмотрим, можем ли мы это сделать. Перепишем данные в виде системы из двух уравнений:

Эта система из двух уравнений с двумя неизвестными имеет решение. Вычтем одно уравнение из другого, чтобы сразу получить значение x.

Подставляя значение x, можно найти y.

По построению этих уравнений такие значения x и y дают нам в обоих возможных вариантах цену портфеля, равной нулю. Рассуждая точно так же, как и в прошлый раз, портфель на expiry в момент времени t₁ стоит ровно ноль, независимо от того, какая цена базового актива реализуется на рынке. Следовательно, этот портфель должен стоить ноль и в момент t₀, по условию отсутствия арбитража. Таким образом, мы получаем уравнение для цены колл-опциона в начальный момент времени. Запишем выражение для цены колл-опциона C₀ в момент времени t_0, используя наше решение.

Где q — новый параметр, который выражается через известные нам коэффициенты: 

По построению, так как мы задали параметры u, d и дискаунт-фактор D₁^-1 так, как показано на рис. 4, то значение q лежит в диапазоне от нуля до единицы. То есть в диапазонах, доступных для значений вероятности.

В слагаемом с C_u мы используем q, а для выплаты C_d при движении вниз мы используем (1-q). То есть формулу можно переписать как вычисление математического ожидания, но используя уже не вероятность p, которая соответствует реальной вероятности того, что произойдет на рынке, а некоторую синтетическую вероятность, которая определяется формулой для q. Иначе говоря, мы получили математическое ожидание дисконтированной выплаты, но используя уже некоторые другие вероятности. Это и является вычислением математического ожидания в риск-нейтральной мере.

Вероятность, которую мы получили, это некоторая синтетическая вероятность, которая отличается от реальных вероятностей, которую мы могли бы наблюдать в реальной жизни, но вычисление математического ожидания от дисконтированной выплаты опциона в этой вероятностной мере дает нам правильный ответ для цены опциона.

Такой подход работает и в более сложных моделях, с непрерывным временем и более приближенным к реальности распределением вероятностей. В таких моделях так же, при условии отсутствия арбитража, можно доказать существование риск-нейтральной вероятностной меры, которая позволяет считать цены инструментов как мат. ожидание в этой мере.

На первый взгляд может показаться: то, что «вероятности» в этой синтетической риск-нейтральной мере никак не связаны с реальными вероятностями возможных исходов, должно сделать их непригодными для практического использования. Но на самом деле это не является препятствием для того, чтобы мат. ожидание, вычисленное в этой синтетической вероятностной мере, имело практическое значение. Нужно только что бы по наблюдаемым на рынке ценам можно было рассчитать нужные риск-нейтральные вероятности. Тогда разные участники рынка смогут прийти к одним и тем же результатам, при этом их оценка реальных вероятностей разных событий может различаться.

Многошаговая биномиальная модель

Подход, описанный здесь для рассуждения про риск-нейтральные вероятности, стал популярен благодаря статье Cox, J. C.; Ross, S. A.; Rubinstein, M. (1979). «Option pricing: A simplified approach». Такой подход помогает решить сразу несколько важных проблем.

Во-первых, после публикаций статей Блэка, Шоульца и Мертона в 1973 году появилось успешная, быстро и широко принятая теория прайсинга опционов. Эту теорию нужно было преподавать в университетах. В том числе MBA-студентам и студентам экономических факультетов. Но разделы математики, которые используются для рассуждений, в общем виде в стандартную программу не входят. Даже сегодня и даже для студентов технических специальностей. А преподавать как-то нужно. Ведь MBA-программа — это не только красивый диплом для студентов, но и дополнительный заработок для преподавателей математики.

Во-вторых, на одном шаге с двумя исходами статья не заканчивается. Если сложить много таких маленьких шагов, то получается многошаговая модель с полезными свойствами. Ее можно использовать для реализации вычислительного алгоритма.

Если у нас есть фиксированный отрезок времени до expiry опциона, то можно попробовать построить математическую модель, в которой мы разделим этот отрезок на N отрезков, и сказать, что на каждом шаге возможно два исхода. Тогда мы получим решетку возможным исходов (см. рис.6). Тут, как и раньше, голубыми цветом нарисованы возможные значения рискового актива, малиновым цветом нарисован рост безрискового актива. Для рискового актива для каждого значения спота есть два варианта развития ситуации на следующем шаге по времени. Линии между голубыми точками показывают, как они связаны друг с другом.

Далее можно математически проанализировать предельный случай при N → ∞. Что и было сделано авторами статьи. Если правильно выбрать параметры u и d, то в пределе решётка будет приближаться к логнормальному распределению. Т.е. в пределе получаем модель Блэка-Шоульца.

Математический анализ такого предельного случая рассматривать не будем, просто приведём некоторую визуализацию. На рис. 7 и 8 нарисованы решетки при больших значениях N. В отличии от рис. 6 нарисованы только точки, показывающие возможные значения, линий между ними нет, чтобы можно было разглядеть детали.

Все статьи этой серии:

• Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч. 1

• Облигации: купонные и бескупонные, расчет доходности. Ликбез для гика, ч. 2

• Облигации: оценка рисков и примеры использования. Ликбез для гика, ч. 3

• Как банки берут друг у друга в долг. Плавающие ставки, процентные свопы. Ликбез для гика, ч. 4

• Построение кривой дисконтирования. Ликбез для гика, ч. 5

• Что такое опционы и кому это нужно. Ликбез для гика, ч. 6

• Опционы: пут-колл парити, броуновское движение. Ликбез для гика, ч. 7