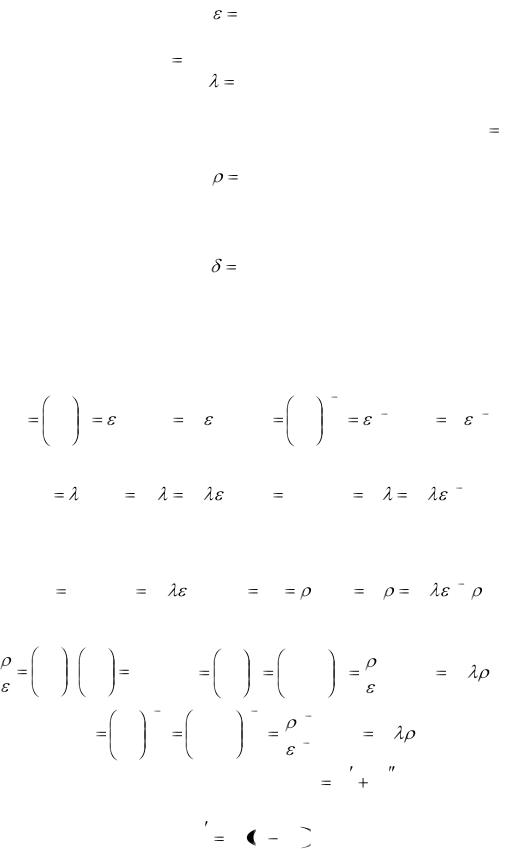
95
масса и объем смеси в цилиндре. Поэтому в термодинамических циклах они отсутствуют.
Важнейшими характеристиками всякого цикла ДВС являются следующие безразмерные величины.
Степень сжатия – отношение удельного объема рабочего тела, соответствующего началу сжатия (точка 1), к удельному объему в конце сжатия (точка 2):
|
v1 / v2 . |
|
|
Степень изохорного повышения давления – отношение давления в конце |
|
|
процесса подвода тепла при v |
const к давлению конца сжатия |
|
p3 / p2 . |
|
|
Степень предварительного (изобарного) расширения – отношение |
|
|
удельного объема в конце |
процесса подвода теплоты при р const к |
удельному объему в начале этого процесса
v4 / v3 .
Степень последующего расширения – отношение удельных объемов в конце и в начале процесса адиабатного расширения. Последняя величина равна объему в конце процессов подвода теплоты
v5 / v4 .
Значение основных характеристик оказывают решающее влияние на величину работы ДВС и его экономичность.
Параметры рабочих процессов, определяемые при рассмотрении отдельных процессов, находят по формулам:
– в точке 2
|
k |
k |
1 |
|||||||||||||
|
р2 |
v1 |
k |
k |
; |
T2 |
v1 |
k 1 |
k 1 |
. |
||||||
|
; p2 |
p1 |
; T2 |
T1 |
||||||||||||
|
р1 |
v2 |
T1 |
v2 |
||||||||||||
– в точке 3
|
р3 |
; |
p р |
p |
k ; |
T3 |
р3 |
; |
T T |
Т |
k 1 . |
|||||||||||||||||||||||||||||||
|
2 |
1 |
||||||||||||||||||||||||||||||||||||||||
|
р2 |
3 |
1 |
T2 |
р2 |
3 |
2 |
|||||||||||||||||||||||||||||||||||
|
– в точке 4 |
|||||||||||||||||||||||||||||||||||||||||
|
р |
р ; |
p |
p |
k ; |
T4 |
v4 |
; |
T T |
Т |
k 1 ; |
|||||||||||||||||||||||||||||||
|
4 |
4 |
1 |
|||||||||||||||||||||||||||||||||||||||
|
3 |
1 |
T3 |
v3 |
4 |
3 |
||||||||||||||||||||||||||||||||||||
|
– в точке 5 |
|||||||||||||||||||||||||||||||||||||||||
|
v4 |
v1 |
v4 |
p5 |
v4 |
k |
v4 |
v2 |
k |
k |
||||||||||||||||||||||||||||||||
|
: |
; |
; |
p |
p |
k ; |
||||||||||||||||||||||||||||||||||||
|
k |
|||||||||||||||||||||||||||||||||||||||||
|
v3 |
v2 |
v1 |
p4 |
v5 |
v2 v1 |
5 |
1 |
||||||||||||||||||||||||||||||||||
|
T5 |
k |
1 |
k |
1 |
k |
1 |
|||||||||||||||||||||||||||||||||||
|
v4 |
v4 v2 |
||||||||||||||||||||||||||||||||||||||||
|
; |
T5 |
Т1 |
k |
. |
|||||||||||||||||||||||||||||||||||||
|
T4 |
v5 |
v2 |
v1 |
k |
1 |
||||||||||||||||||||||||||||||||||||
|
Количество |
подведенной |
теплоты |
q1 |
q1 |
q2 |
и |
отведенной q2 |
||||||||||||||||||||||||||||||||||
|
определяются |
|||||||||||||||||||||||||||||||||||||||||
|
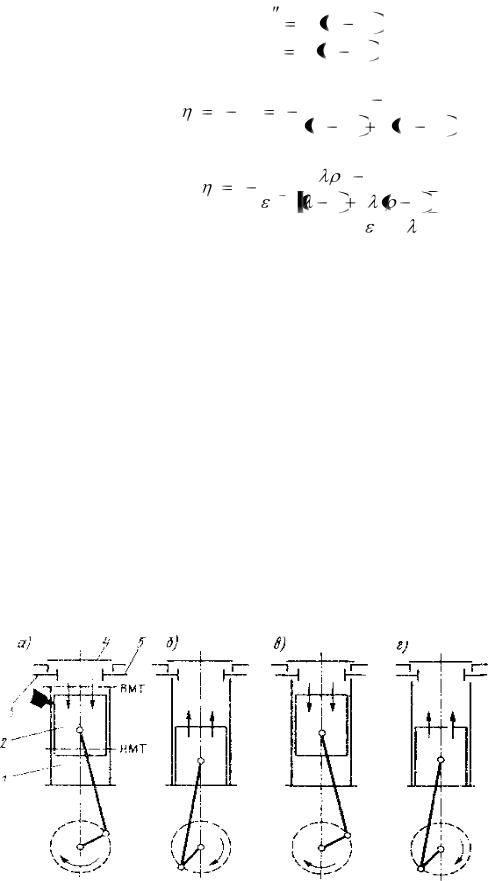
q1 |
cv T3 T2 |
; |
|
96 |
||||||||||||||
|
q2 |
cp T4 |
T3 |
; |
|||||||||||
|
q2 |
cv T5 |
T1 . |
||||||||||||
|
Термический кпд цикла будет |
||||||||||||||
|
1 |
q2 |
1 |
T5 |
T1 |
. |
|||||||||
|
t |
||||||||||||||
|
q1 |
T3 |
T2 |
k T4 |
T3 |
||||||||||
|
Подставив значения температур в формулу, получим |
||||||||||||||
|
k |
1 |
|||||||||||||
|
1 |
. |
|||||||||||||
|
t |
||||||||||||||
|
k |
1 |
1 |
k |
1 |
||||||||||
|
Отсюда следует, что с увеличением |
k, |
и |
кпд цикла возрастает, а с |
увеличением 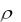
Цикл со смешанным подводом теплоты обобщает циклы с изобарным и изохорным подводом теплоты.
ЦИКЛЫ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
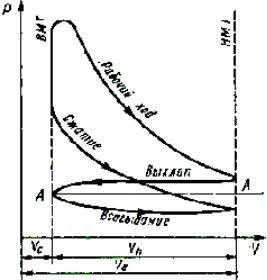
Назначение всякого теплового двигателя состоит в преобразовании теплоты в работу. Необходимая для перевода в работу теплота получается при сгорании жидких, твердых или газообразных теплив. Топливо может сжигаться вне тепловой машины — это так называемые двигатели внешнего сгорания. Двигатели, в которых процесс сгорания осуществляется в рабочем пространстве машины, называют двигателями внутреннего сгорания (ДВС). Рабочий процесс поршневого двигателя внутреннего сгорания заключается в следующем (рис. 11.1). Горючая смесь (смесь топлива с воздухом) сгорает в цилиндре 1 с повышением температуры и давления. Продукты сгорания, воздействуя на поршень 2, перемещают его из крайнего верхнего положения (верхняя мертвая точка — ВМТ) в крайнее нижнее (нижняя мертвая точка — НМТ) (рис. 11.1, а).
Рис. 11.1. Рабочий процесс поршневого двигателя внутреннего сгорания
Процессы сгорания и расширения дают в совокупности рабочий ход (такт поршня). Чтобы можно было повторить эти основные процессы в двигателе, отработавшие продукты сгорания нужно удалить из цилиндра и наполнить его свежей порцией горючей смеси. Это происходит за два (такта) хода поршня:
97
прямой ход — выталкивание продуктов сгорания (рис. 11.1,б) и обратный ход
— всасывание воздуха или горючей смеси (рис. ИЛ, в). Процессы выталкивания и всасывания осуществляются при соответствующем открытии выхлопного 5 и всасывающего 3 клапанов, помещенных в головке цилиндра 4. Во время четвертого хода поршня производится сжатие воздуха или горючей смеси (рис. 11.1, г), и затем все процессы повторяются. Таким образом, рабочий процесс периодичен и каждый период складывается из четырех ходов поршня, производимых за два полных оборота коленчатого вала двигателя. Двигатели, работающие таким образом, называют четырехтактными. Двигатели, у которых процесс совершается за два хода поршня (один оборот коленчатого вала), называются двухтактными. У них ход выталкивания и всасывания заменяется продувкой цилиндра, во время которой удаляются продукты сгорания и цилиндр заполняется воздухом или горючей смесью.
|
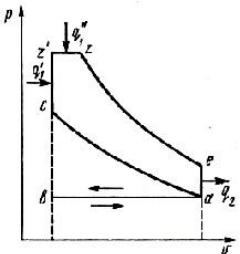
Рис. 11.2 Индикаторная диаграмма |
ДВС |
Рабочие процессы в двигателях исследуются с помощью особых приборов —
индикаторов. Они позволяют получить индикаторные диаграммы,
отображающие изменение давления в цилиндре двигателя. На индикаторных диаграммах по оси ординат откладываются абсолютные давления внутри цилиндра, а по оси абсцисс — соответствующие этому давлению изменения объема или перемещения поршня (рис. 11.2).
98
Рис. 11.3 Теоретическая индикаторная диаграмма ДВС
На рисунке А-А — линия атмосферного давления.
Индикаторная диаграмма дает возможность исследовать совершенство рабочих процессов в двигателе и определить индикаторные параметры двигателя: работу, кпд, мощность, удельный расход топлива. На рис. 11.3 представлена теоретическая индикаторная диаграмма, на которой линией b-а изображен процесс всасывания, линией а-с — процесс сжатия; c-z — процесс горения при постоянном объеме z`-z — процесс горения при постоянном давлении, z-e — процесс расширения продуктов сгорания, линией е-а-b— процесс выхлопа продуктов сгорания в атмосферу. На теоретической индикаторной диаграмме процессы сжатия и расширения — это политропные процессы с показателями политроп n1= 1,3… 1,38 и n2= 1,2… 1,32, зависящими от теплообмена между рабочим телом и стенками двигателя. Процессы всасывания b-a и выталкивания a-b не являются термодинамическими, так как параметры рабочего тела при этом не изменяются.
Площадь под линией всасывания представляет собой работу всасывания LBC, а площадь под линией а-b — работу выталкивания Lвыт. Эти процессы направлены в разные стороны и сумма работ (LBC + Lвыт) равна нулю. Однако индикаторная диаграмма не является круговым обратимым термодинамическим процессом — циклом и не дает возможности сравнительно просто определить изменение состояния рабочего тела в отдельных термодинамических процессах, из которых состоит цикл.
В основе работы двигателей внутреннего сгорания лежат идеальные круговые процессы преобразования теплоты в механическую работу, т. е. идеальные циклы. Изучение их необходимо для оценки совершенства действительных тепловых процессов, происходящих в двигателях, а также факторов, влияющих на экономичность двигателя и развиваемую им работу.
При термодинамическом исследовании циклов полагают, что:



99

процесс уноса теплоты, содержащейся в продуктах сгорания, обратимый процесс отвода теплоты q2 от рабочего тела; механические потери, т. е. потери на трение и потери теплоты в окружающую среду (передача теплоты от стенок и унос теплоты охлаждающей водой), отсутствуют.
При таких предпосылках можно считать, что двигатели внутреннего сгорания работают по обратимым термодинамическим циклам. Термодинамическое исследование дает возможность определить принципы работы двигателей, параметры газа в характерных точках цикла, термический кпд и работу цикла. Термодинамические исследования циклов, как правило, сопровождаются графическиv изображением их на pv- и Ts-диаграммах.
В двигателях внутреннего сгорания могут быть использованы следующие идеальные циклы:
а) цикл со смешанным подводом теплоты как при постоянном объеме, так и при постоянном давлении;
|
б) |
цикл с подводом теплоты при постоянном объеме ( v= const); |
|
в) |
цикл с подводом теплоты при постоянном давлении (р = const). |
Во всех перечисленных циклах отвод теплоты в цикле производится при постоянном объеме в силу того, что расширение газа происходит не полностью и степень возможного расширения в двигателе определяется положением поршня в нижней мертвой точке,
Цикл со смешанным подводом теплоты (цикл Тринклера)
осуществляется в бескомпрессорных дизелях. В цилиндрах дизеля сжимается чистый воздух и происходит самовоспламенение топлива, распыление которого осуществляется механическим путем с помощью насоса или насос-форсунки под давлением 100… 150 МПа.
Ри
Рис.11.4.
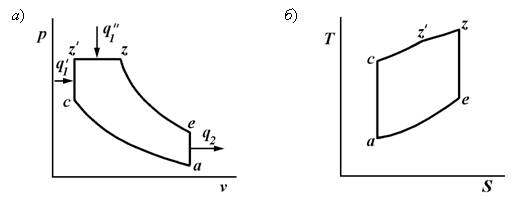
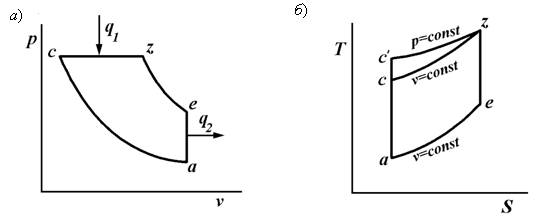
Топливо впрыскивается в камеру сгорания или специальные предкамеры. Процесс сгорания идет вначале с повышением давления, а затем при постоянном давлении. Осуществление такого подвода теплоты характерно для двигателей, работающих по смешанному циклу. При термодинамическом исследовании рассматривают цикл, состоящий из следующих-процессов (рис. 11.4, а, б): а-с — адиабатное сжатие; c-z` — изохорный подвод теплоты; z’-z— изобарный подвод теплоты; z-e — адиабатное расширение; е-а — изохорный
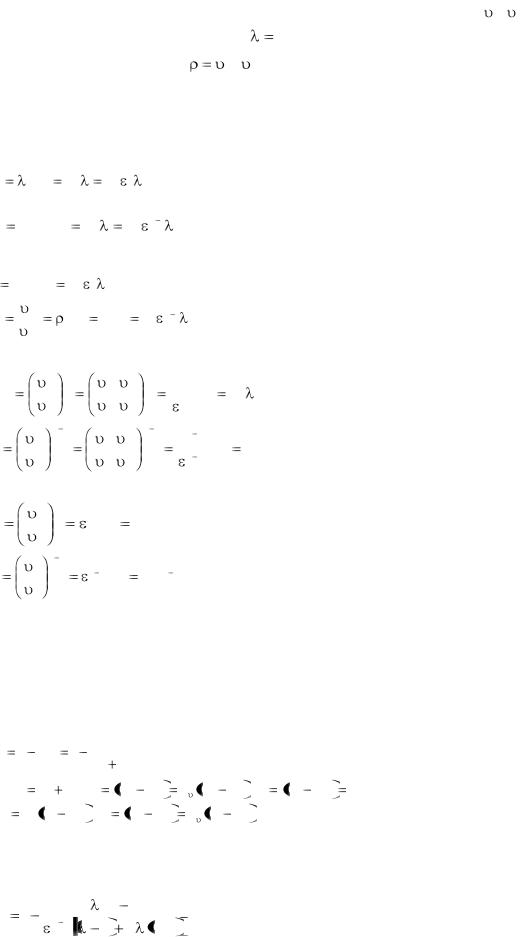
100
отвод теплоты. Цикл является как бы обобщающим для всех циклов поршневых ДВС. Цикл со смешанным подводом определяется заданием начального состояния в точке а и параметрами цикла: степенью сжатия 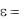
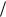
|
изохорного повышения давления |
pz` / pc , степенью предварительного |
|
(изобарного) расширения z / |
z` . |
Степень сжатия представляет собой отношение полного объема цилиндра Va к объему камеры сгорания Vс. Разность между полным объемом и объемом камеры сгорания дает так называемый рабочий объем цилиндра Vh .
в точке z’
|
pz` |
; p |
p |
p |
k |
; |
||||||||||||||||||||||||||||||||||||||||
|
pc |
z` |
c |
a |
||||||||||||||||||||||||||||||||||||||||||
|
Tz` |
pz` |
; T |
T |
T |
k 1 ; |
||||||||||||||||||||||||||||||||||||||||
|
Tc |
pc |
z` |
c |
a |
|||||||||||||||||||||||||||||||||||||||||
|
в точке z |
|||||||||||||||||||||||||||||||||||||||||||||
|
p |
z |
p |
z` |
; p |
z |
p |
a |
k ; |
|||||||||||||||||||||||||||||||||||||
|
Tz |
z |
; T T ρ T |
k 1 |
ρ; |
|||||||||||||||||||||||||||||||||||||||||
|
Tz` |
z |
z` |
a |
||||||||||||||||||||||||||||||||||||||||||
|
z` |
|||||||||||||||||||||||||||||||||||||||||||||
|
в точке е |
|||||||||||||||||||||||||||||||||||||||||||||
|
pe |
k |
k |
ρk |
||||||||||||||||||||||||||||||||||||||||||
|
z |
z |
c |
; p |
p |
ρ |
k |
; |
||||||||||||||||||||||||||||||||||||||
|
pz |
k |
e |
a |
||||||||||||||||||||||||||||||||||||||||||
|
e |
c |
a |
|||||||||||||||||||||||||||||||||||||||||||
|
T |
k |
1 |
k |
1 |
ρk 1 |
||||||||||||||||||||||||||||||||||||||||
|
z |
z |
c |
λρk . |
||||||||||||||||||||||||||||||||||||||||||
|
e |
; T |
T |
|||||||||||||||||||||||||||||||||||||||||||
|
k 1 |
a |
||||||||||||||||||||||||||||||||||||||||||||
|
Tz |
e |
||||||||||||||||||||||||||||||||||||||||||||
|
e |
c |
a |
|||||||||||||||||||||||||||||||||||||||||||
|
в точке с |
|||||||||||||||||||||||||||||||||||||||||||||
|
pc |
k |
||||||||||||||||||||||||||||||||||||||||||||
|
a |
k ;p |
p |
sk ; |
||||||||||||||||||||||||||||||||||||||||||
|
c |
|||||||||||||||||||||||||||||||||||||||||||||
|
pa |
a |
||||||||||||||||||||||||||||||||||||||||||||
|
c |
|||||||||||||||||||||||||||||||||||||||||||||
|
Tc |
k 1 |
||||||||||||||||||||||||||||||||||||||||||||
|
a |
k 1; T T sk 1 |
; |
|||||||||||||||||||||||||||||||||||||||||||
|
Ta |
c |
a |
|||||||||||||||||||||||||||||||||||||||||||
|
c |
Параметры рабочего тела в узловых точках цикла, определяемые при рассмотрении отдельных процессов, находят по формулам:
Термический кпд смешанного цикла
|
ηtсм |
1 |
q |
2 |
1 |
q2 |
, |
||
|
q1 |
` |
q |
` |
|||||
|
q1 |
2 |
|
где |
q |
q` |
q` |
; q` |
u |
u |
c T T ; q« |
h |
h |
|||||
|
1 |
1 |
2 |
1 |
z` |
c |
z` |
c 1 |
z |
z` |
|||||
|
cp Tz |
Tz` ; q2 |
ue |
ua |
c Te |
Ta . |
Подставляя значения соответствующих температур и полагая, что теплоемкости идеального газа величины постоянные, получим
|
ηtсм 1 |
ρk |
1 |
. |
(11.1) |
|
|
k 1 |
1 |
k ρ -1 |
|||
101
Как видно из формулы (11.1), термический кпд цикла растет с увеличением ε и k и уменьшается с увеличением ρ. Степень изохорного повышения давления λ связана с величиной ρ.Чем больше λ, тем меньше ρ (при тех же значениях ε и q2). Тогда с ростом λ термический кпд смешанного цикла увеличивается. Работа теоретического цикла определяется по формуле lц q1 t . Отношение
работы цикла к рабочему объему VH характеризует среднее давление цикла
|
pц |
lц |
lц |
lц |
. |
|||||
|
h |
a |
c |
a |
1 |
|||||
Среднее давление смешанного цикла
|
pa |
k |
||
|
pц |
1 k ρ -1 ηtсм (11.2) |
||
|
k 1 |
1 |
||
Наиболее эффективным способом увеличения среднего давления цикла является повышение начального давления — наддув двигателя. Рассмотренный идеальный цикл лежит в основе работы всех современных дизелей.
Цикл с подводом теплоты при постоянном объеме (цикл Отто) является частным случаем рассмотренного выше, когда степень изобарного расширения
ρ=1.
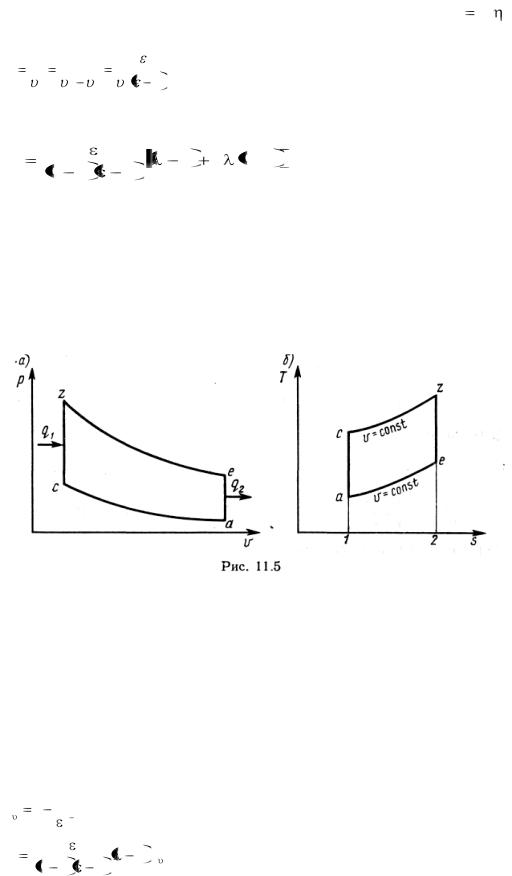
Рис.11.5.
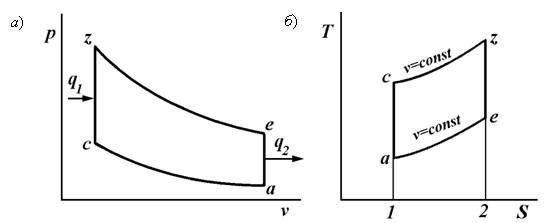
По этому циклу работают двигатели, в цилиндрах которых сжимается топливно-воздушная смесь до давления 1,0… 1,5 МПа и поджигается в конце сжатия от электрической искры. Идеальный цикл Отто (рис. 11.5, а, б) состоит из процессов адиабатного сжатия а-с, подвода к рабочему телу теплоты при v=const — c-z, адиабатного расширения z-e и отдачи рабочим телом теплоты при v=const — е-а. Параметры в узловых точках цикла определяются аналогично циклу со смешанным подводом теплоты. Формулы для определения ηt и pц в этом цикле получаются из соответствующих формул для смешанного цикла при ρ=1 :
|
ηt 1 |
1 |
; |
(11.3) |
|||
|
k 1 |
||||||
|
k |
||||||
|
pц |
pa |
1 ηt . |
(11.4) |
|||
|
k |
1 |
1 |
||||
Из выражения (11.3) видно, что термический кпд цикла с подводом теплоты при v=const зависит от степени сжатия и показателя адиабаты k рабочего тела,

102
совершающего цикл. Несмотря на то что с увеличением степени сжатия растут термический кпд и полезная работа цикла при. больших степенях сжатия (ε<10), в результате значительного повышения температуры в конце процесса сжатия может наступить самовоспламенение смеси. Еще более существенным является то обстоятельство, что с увеличением степени сжатия, а следовательно, и с увеличением температуры в конце сжатия появляется детонация свежей рабочей смеси, которая приводит к взрывному характеру сгорания. В результате детонации процесс сгорания нарушается, мощность двигателя падает, расход топлива растет. По этой причине двигатели, работающие по циклу v=const, имеют вполне определенные предельные значения степени сжатия (ε =5,5 …9,0).
Явление детонации в значительной степени зависит от сорта применяемого топлива, от его антидетонационных качеств. Поэтому сорт применяемого топлива определяет выбор предельного значения степени сжатия для двигателей легкого топлива.
Цикл с подводом теплоты при постоянном давлении (цикл Дизеля)
является также частным случаем обобщающего цикла при λ=1. В двигателях дизеля раздельно сжимается воздух до давления 4,0… 5,0 МПа и смесь топлива с воздухом, сжатым во вспомогательном компрессоре. Подача топлива осуществляется так, чтобы давление в процессе сгорания оставалось постоянным.
Идеальный цикл дизеля состоит из двух адиабат сжатия и расширения, изобары подвода теплоты и изохоры отвода теплоты (рис. 11.6, а, б). Термический кпд и среднее давление цикла из (11.1) и (11.2) при λ=1 равны:
|
ηtp 1 |
ρk |
1 |
; |
(11.5) |
||
|
k |
k 1 |
ρ -1 |
||||
|
pц |
pa k k |
ρ 1 ηtρ . |
(11.6) |
|||
|
k |
1 |
1 |
||||
Влияние ε на ηtpтакое же, как и в предыдущих циклах, т. е. с увеличением степени сжатия увеличивается и термический кпд цикла. При увеличении степени предварительного расширения ρ, как видно из формулы (11.5), термический кпд цикла должен падать. При постоянной степени сжатия увеличение ρ вызовет увеличение объема z , который зависит от подводимого
|
103 |
|
|
количества теплоты q1. При увеличении q1 увеличивается объем |
z , а вместе с |
|
ним увеличивается и работа цикла. Таким образом, возрастание ρ |
приводит к |
|
увеличению работы и уменьшению термического кпд. |
Сопоставляя значения термических кпд циклов с подводом теплоты при =
|
const |
и p = const, видим, что они различаются множителем |
||
|
ρk |
1 |
1. |
|
|
k ρ -1 |
|||
|
Отсюда следует, что при одинаковых степенях сжатия |
ηt ηtp . |
Рис.11.7. Рис.11.8.
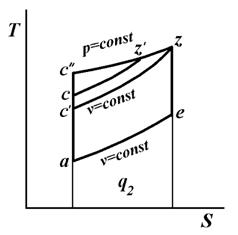
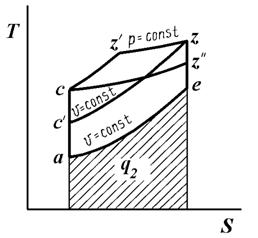
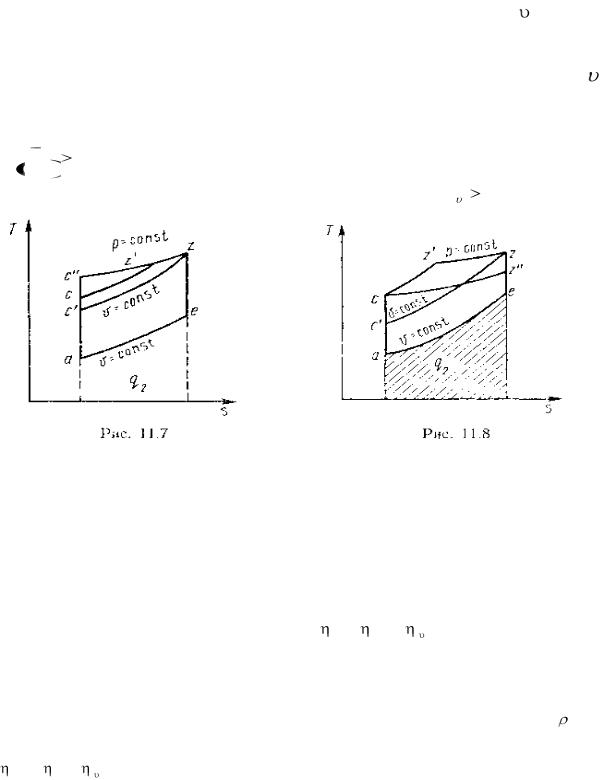
Термодинамическая эффективность каждого из рассмотренных циклов зависит от конкретных условий его осуществления. Целесообразнее сравнивать циклы при различных степенях сжатия ε, но при одинаковых максимальных давлениях и температурах и одинаковом отведенном количестве теплоты q2 .
Из Ts -диаграммы (рис. 11.7) следует, что наибольший термический кпд будет у цикла с подводом теплоты при р=const: tp 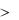
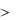
имеет промежуточное значение по сравнению с циклами с подводом теплоты при р =const и v = const.
При оптимальных степенях сжатия (цикл Отто — ε<10, цикл Дизеля и
смешанный — ε =16 и 22 соответственно) λu=3,2 … 4,2, λсм =1,6 …2,0, см =1,3…
1,7,
tсм 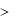
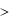
что видно из рис. 11.8. Поэтому все выпускаемые сейчас дизели работают по смешанному циклу.
Цикл стирлинга
Двигатель Стирлинга — газовый двигатель поршневого типа с внешним подводом теплоты, которая получается в результате сгорания твердых, жидких, газообразных топлив. Внешний подвод теплоты осуществляется через теплопроводящую стенку. Рабочее тело (водород, гелий, аргон, углекислый газ) находится в замкнутом пространстве и во время работы не заменяется.
q2«
104
Одна из возможных конструктивных схем двигателя Стирлинга, когда рабочий 5, и вытеснительный 1 поршни находятся в одном цилиндре, дана на рис.11.9.
Рис.11.9. Схема двигателя Стирлинга
В процесе перекачки в горячую полость (над рабочим поршнем) рабочее тело в регенераторе 3 и нагревателе 4 получает теплоту, а в процессе перекачки в холодную полость (под рабочим поршнем) отдает теплоту в регенераторе 3 и охладителе 2. Для осуществления этих процессов движение вытеснительного поршня 1 сдвинуто по фазе по отношению к движению рабочего поршня 5.
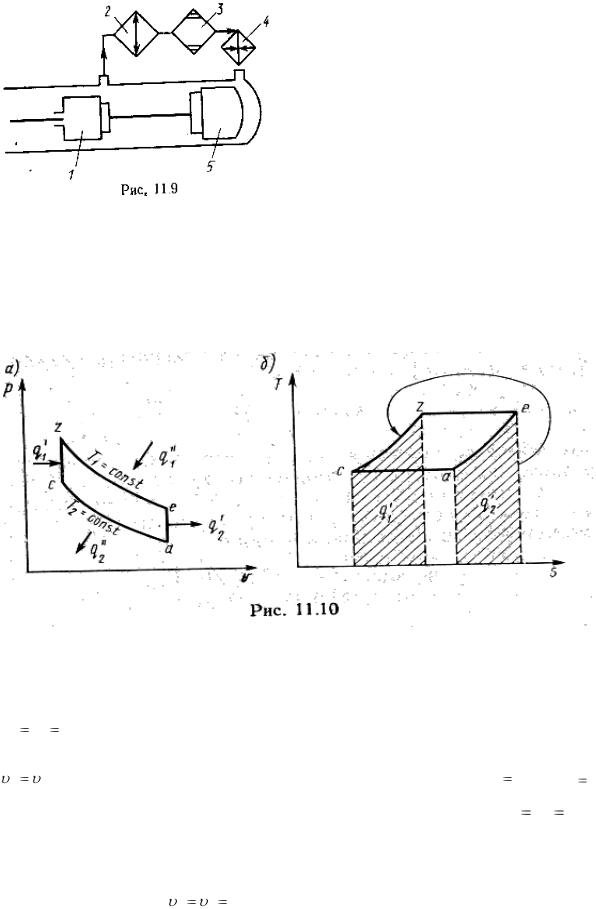
Рис.11.10. Идеальный цикл Стирлинга
Идеальный цикл Стирлинга состоит из четырех процессов (рис. 11.10, а, б). В процессе а-с холодное рабочее тело сжимается в изо-термическом процессе
Ta Tc T2 при интенсивном отводе теплоты . В процессе c-z поршеньвытеснитель перемещает рабочее тело из холодной полости в горячую, так что
|
c z |
(изохорный процесс), а температура увеличивается от |
Tc |
T2 |
до |
T |
T |
при |
|||
|
z |
1 |
|||||||||
|
подводе теплоты |
q` |
T |
T |
T |
к |
|||||
|
1 . В изотермическом процессе расширения |
z |
e |
1 |
|||||||
|
рабочему телу подводится теплота q2« |
. Затем поршень-вытеснитель, |
перемещаясь в обратном направлении, выталкивает рабочее тело из горячей
полости в холодную const с отводом теплоты q` . Отличительной
e a 2
особенностью цикла Стирлинга является то, что рабочее тело, перемещаясь из
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7.2. Циклы двигателей внутреннего сгорания (ДВС)
Циклы поршневых
двигателей внутреннего сгорания подразделяют на три группы:
- с
подводом теплоты при постоянном объеме (карбюраторные ДВС); - с
подводом теплоты при постоянном давлении (компрессорные дизели); - со
смешанным подводом теплоты при постоянном объеме (безкомпрессорные
дизели);
Основными
характеристиками или параметрами любого цикла теплового двигателя являются
следующие безрамерные величины:
степень сжатия
(отношение удельных
объемов рабочего тела в начале и конце сжатия)
e = n1
/ n2 , (7.5)
степень
повышения давления (отношение давлений в конце и в начале
изохорного процесса подвода теплоты)
l = Р3 / Р2
, (7.6)
степень
предварительного расширения или степень изобарного расширения
(отношение удельных объемов в конце и в начале изохорного процесса подвода
теплоты)
r = n3
/ n2 . (7.7)
1). Рассмотрим
цикл
ДВС с подводом теплоты при постоянном объеме
на примере
четырехтактного двигателя.
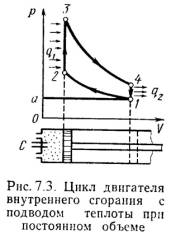
Диаграмма реального двигателя представлена на рис.7.3.
а-1 (1 такт) – в цилиндр через всасывающий клапан поступает смесь воздуха и
паров горючего (нетермодинамичемкий процесс);
1-2 (2 такт) – адиабатное сжатие (повышается температура);
2-3 – сгорание горючей смеси, давление быстро возрастает при постоянном объеме
(подвод теплоты q1);
3-4 (3 такт) – адиабатное расширение (рабочий процесс, совершается полезная
работа);
4-а – открывается выхлопной клапан и отработанные газы покидают цилиндр
давление цилиндра падает (отводится тепло q2).
1-а (4 такт) – выталкивание оставшихся в цилиндре газов.
Затем процесс повторяется.
Описанный процесс является необратимым (наличие трения, химической реакции в
рабочем теле, конечные скорости поршня, теплообмен при конечной разности
температур и т.п.).
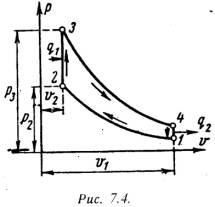
Для анализа теории тепловых машин термодинамика рассматривает идеальные циклы
обратимые циклы. Диаграмма идеального процесса двигателя внутреннего сгорания
показана на рис.7.4.
Из этой диаграммы выводится формула для термического к.п.д. цикла с подводом
теплоты при постоянном объеме, который имеет следующий вид:
ht = 1 – 1/eg , (7.8)
где: e –степень сжатия
(основной показатель работы двигателя, чем выше е, тем выше экономичность ДВС);
g – показатель
адиабаты.
2). Идеальный
цикл ДВС со смещанным
подводом теплоты при постоянном объеме
(безкомпрессорные
дизели). Диаграмма цикла показана на рис.7.5.
1-2 — чистый воздух с температурой Т1 сжимается до температуры Т2,
которая больше температуры воспламенения топлива. В этот момент в цилиндр через
форсунки под давлением впрыскивается топливо.
2-3 – горючая смесь самовоспламеняется и к рабочему телу подводится тепло q1/,
давление повышается до Р3.
3-4 – поршень перемешается обратно, поступление и сгорание топлива продолжается
при постоянном давлении и подводится тепло q1//.
4-5 – поршень продолжает перемещаться в нижнюю мертвую точку, давление падает
(адиабатное расширение);
5-1 – процесс отвода теплоты q2 при постоянном объеме (через
выпускной клапан покидают отработанные газы).
Термический к.п.д. цикла определяется по формуле:
ht = l – (l·rg – 1) /
eg-1·[(l — 1) + g·l·(r – 1)] . (7.9)
Цикл двигателей с подводом теплоты при постоянном давлении широкое
применение не нашли, так как у этих циклов очень большой коэффициент сжатия.
По формуле зt для нескольких значений:
с=0,75с-1,25с
при постоянных значениях л и е
|
с1=0,75*2=1,5 с2=0,85*2=1,7 с3=0,95*2=1,9 |
с4=1,05*2=2,1 с5=1,15*2=2,3 с6=1,25*2=2,5 |
зt=1-1/(еk-1)*(л*сk-1)/(л-1+k*л*(с-1))
зt1=1-0,338*(1,5*1,51,3717-1)/(1,5-1+1,3717*1,5*(1,5-1))=0,6427
зt2=1-0,338*(1,7*1,51,3717-1)/(1,5-1+1,3717*1,5*(1,7-1))=0,6331
зt3=1-0,338*(1,9*1,51,3717-1)/(1,5-1+1,3717*1,5*(1,9-1))=0,6237
зt4=1-0,338*(2,1*1,51,3717-1)/(1,5-1+1,3717*1,5*(2,1-1))=0,6146
зt5=1-0,338*(2,3*1,51,3717-1)/(1,5-1+1,3717*1,5*(2,3-1))=0,6058
зt6=1-0,338*(2,5*1,51,3717-1)/(1,5-1+1,3717*1,5*(2,5-1))=0,5974
Влияние степени изобарного расширения на термический КПД цикла показано в приложении 2.
Результаты расчетов представлены в виде таблицы.
Результаты исследования цикла ДВС.
|
Характеристики цикла |
Постоянные параметры |
|||||||||||||||||
|
л |
с |
е |
л |
е |
с |
|||||||||||||
|
1,5 |
1,7 |
13,5 |
1,5 |
13,5 |
1,7 |
|||||||||||||
|
Переменные параметры и их значения |
||||||||||||||||||
|
е1 |
е2 |
е3 |
е4 |
е5 |
е6 |
с1 |
с2 |
с3 |
с4 |
с5 |
с6 |
л1 |
л2 |
л3 |
л4 |
л5 |
л6 |
|
|
13,875 |
15,725 |
17,575 |
19,425 |
21,275 |
23,125 |
1,5 |
1,7 |
1,9 |
2,1 |
2,3 |
2,5 |
1,125 |
1,275 |
1,425 |
1,575 |
1,725 |
1,875 |
|
|
зt % |
57,6 |
59,5 |
61,2 |
62,6 |
63,8 |
64,9 |
64,3 |
63,3 |
62,4 |
61,5 |
60,6 |
59,7 |
61,3 |
61,6 |
61,8 |
62,0 |
62,1 |
62,2 |
Анализ
В ДВС с воспламенением рабочей смеси (около ВМТ) от электрической искры время сгорания очень мало, в связи, с чем допустимо принять, что процесс подвода теплоты осуществляется при постоянном объеме (процесс 3 — 2 и процесс 5 — 1). В рассматриваемом цикле степень предварительного расширения с равна единице.
Таким образом, термический КПД цикла с подводом теплоты при постоянном объеме зависит от свойств рабочего тела и конструкции двигателя. Это иллюстрируется графиком (приложение 2), который показывает, что термический КПД двигателя увеличивается по мере увеличения степени сжатия е.
Нагрузка на двигатель в термодинамическом цикле характеризуется количеством теплоты, подводимый к рабочему телу от горячего источника. Для цикла с подводом теплоты при постоянном объеме(V=const).
Следовательно, нагрузка при заданных значениях Сv и Т2 пропорциональна степени повышения давления л и не зависит от степени сжатия е. Это свидетельствует о том, что термический КПД при изменении нагрузки не меняется.
Показывает, что с увеличением количества подведенной теплоты (степень повышения давления л) среднее давление цикла с также увеличивается.
В цилиндрах двигателей внутреннего сгорания с воспламенением от сжатия при такте сжатия сжимается чистый воздух. Вблизи от ВМТ в цилиндр двигателя через форсунку впрыскивается распыленное топливо, которое в среде горячего воздуха самовоспламеняется и сгорает.
Процесс подвода теплоты к рабочему телу принимается в этом случае изобарным (Р=const).
зt=1-1/(еk-1)*(л*сk-1)/(л-1+k*л*(с-1)).
Данная формула показывает, что термический КПД рассматриваемого цикла увеличивается при возрастании степени сжатия е (приложение 2) и уменьшается при возрастании степени предварительного расширения с (приложение 2).
При увеличении нагрузки двигателя, то есть при увеличении количества подведенной теплоты, увеличивается степень предварительного расширения с и не изменяется степень сжатия. Следовательно, по мере увеличения нагрузки двигателя термический КПД цикла при постоянном давлении уменьшается (приложение 2). Это подтверждается sT — диаграммой (приложение 1), показывающей, что по мере увеличения подвода теплоты выигрыш в работе цикла от дополнительных количеств теплоты постепенно уменьшается.
Содержание:
- Тепловое расширение твердых и жидких тел
- Зависимость объёма тел от температуры
- Линейное расширение твёрдых тел
- Объёмное расширение твёрдых тел
- Учёт теплового расширения в технике
- Терморегулятор
- Тепловое расширение жидкостей
Тепловое расширение – это изменение размеров и формы тел при изменении температуры. Математически можно высчитать объемный коэффициент расширения, позволяющий спрогнозировать поведение газов и жидкостей в изменяющихся внешних условиях. Чтобы получить такие же результаты для твердых тел, необходимо учитывать коэффициент линейного расширения.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Тепловое расширение твердых и жидких тел
Тепловое расширение (также используется термин «термическое расширение») — это изменение линейных размеров и формы тела при изменении его температуры. Количественно тепловое расширение жидкостей и газов при постоянном давлении характеризуется изобарным коэффициентом расширения (объёмным коэффициентом теплового расширения). Для характеристики теплового расширения твёрдых тел дополнительно вводят коэффициент линейного теплового расширения.
Зависимость объёма тел от температуры
Частицы твёрдого тела занимают друг относительно друга определённые положения, но не остаются в покое, а совершают колебания. При нагревании тела увеличивается средняя скорость движения частиц. Средние расстояния между частицами при этом увеличиваются, поэтому увеличиваются линейные размеры тела, а следовательно, увеличивается и объём тела.
При охлаждении линейные размеры тела сокращаются, и объём его уменьшается.
При нагревании, как известно, тела расширяются, а при охлаждении сжимаются. Качественная сторона этих явлений была уже рассмотрена в начальном курсе физики.
Наша задача теперь — ознакомиться с количественными законами этих явлений.
Линейное расширение твёрдых тел
Твёрдое тело при данной температуре имеет определённую форму и определённые линейные размеры. Увеличение линейных размеров тела при нагревании называется тепловым линейным расширением.
Измерения показывают, что одно и то же тело расширяется при различных температурах по-разному: при высоких температурах обычно сильнее, чем при низких. Но это различие в расширении столь невелико, что при сравнительно небольших изменениях температуры им можно пренебречь и считать, что изменение размеров тела пропорционально изменению температуры.
В начальном курсе физики было установлено, что различные вещества по-разному расширяются при нагревании: одни сильнее, другие слабее; железо, например, расширяется сильнее стекла и слабее меди.
Чтобы количественно характеризовать это важное тепловое свойство тел, введена особая величина, называемая коэффициентом линейного расширения.
Пусть твёрдое тело при температуре 0°С имеет длину 




Величина 
Формула (1) показывает, что при t = 1°С и 


Из формулы (1) следует, что наименованием коэффициента 
Формулу (1) можно записать в следующем виде:
Отсюда легко определить длину тела при любой температуре, если известны его начальная длина и коэффициент линейного расширения.
Ниже в таблице приведены коэффициенты линейного расширения некоторых веществ, определённые на опыте.
Объёмное расширение твёрдых тел
При тепловом расширении твёрдого тела с увеличением линейных размеров тела увеличивается и его объём. Аналогично коэффициенту линейного расширения для характеристики объёмного расширения можно ввести коэффициент объёмного расширения. Опыт показывает, что так же, как и в случае линейного расширения, можно без большой ошибки принять, что приращение объёма тела пропорционально повышению температуры.
Обозначив объём тела при 0°С через V0 , объём при температуре t0 через Vt а коэффициент объёмного расширения через 

При V0 = 1 ед. объёма и t = 1°С величина а равна Vt— V0, т. е. коэффициент объёмного расширения численно равен приросту объёма тела при нагревании на 1°С, если при 0°С объём был равен единице объёма.
По формуле (2), зная объём тела при температуре 0°С, можно вычислить объём его при любой температуре t°:
Установим соотношение между коэффициентами объёмного и линейного расширения.
Допустим, что имеем кубик, ребро которого при 0° С равно 1 см. При нагревании на 1°С ребро станет равным 

Можно написать следующее равенство:
Но
В этой формуле величины 

Коэффициент объёмного расширения твёрдого тела равен утроенному коэффициенту линейного расширения.
Учёт теплового расширения в технике
Из таблицы на странице 124 видно, что коэффициенты расширения твёрдых тел очень малы. Однако самые незначительные, изменения размеров тел при изменении температуры вызывают появление огромных сил.
Опыт показывает, что даже для небольшою удлинения твёрдого тела требуются огромные внешние силы. Так, например, чтобы увеличить длину стального стержня сечением в 1 см2 приблизительно на 0,0005 его первоначальной длины, необходимо приложить силу в 1000 кГ. Но такой же величины расширение этого стержня получается при нагревании его на 50°С. Ясно поэтому, что, расширяясь при нагревании (или сжимаясь при охлаждении) на 50°С, стержень будет оказывать давление около 1000 
Огромные силы, возникающие при расширении и сжатии твёрдых тел, учитываются в технике. Так, например, один из концов моста не закрепляют неподвижно, а устанавливают на катках; железнодорожные рельсы не укладывают вплотную, а оставляют между ними просвет; паропроводы подвешивают на крюках, а между отдельными трубами устанавливают компенсаторы, изгибающиеся при удлинении труб паропровода. По этой же причине котёл паровоза закрепляется только на одном конце, другой же его конец может свободно перемещаться.
Огромное значение имеет расширение от нагревания при точных измерениях. В самом деле, если масштабная линейка или калибр, которыми проверяются размеры изготовленной части машины, значительно изменяют свою величину, то необходимой точности при измерении не получится. Для избежания грубых ошибок при измерении или контроле изготовленные изделия заблаговременно приносят в помещение, где производятся измерения, чтобы они успели принять температуру калибров. Самые калибры и измерительные инструменты делают из материала с очень малым коэффициентом расширения. Таким материалом, например, является особая железо-никелевая сталь — инвар, с коэффициентом расширения 0,0000015.
Рис. 132а. Схема устройства металлического термометра.
Как показывает таблица на странице 124, платина и стекло имеют одинаковый коэффициент расширения; поэтому можно вплавлять платину в стекло, причём после охлаждения не происходит ни ослабления связи обоих веществ, ни растрескивания стекла. В электрических лампочках в стекло вплавляется железо-никелевая проволока, имеющая такой же коэффициент расширения, как и стекло. Заслуживает внимания очень малый коэффициент расширения у кварцевого стекла. Такое стекло выдерживает, не лопаясь и не растрескиваясь, неравномерное нагревание или охлаждение. Так, например, в раскалённую докрасна колбочку из кварцевого стекла можно вливать холодную воду, тогда как колба из обычного стекла при таком опыте лопается. Указанная особенность кварцевого стекла является следствием малости его коэффициента теплового расширения.
Терморегулятор
Две одинаковые полоски из разных металлов, например из железа и латуни, склёпанные вместе, образуют так называемую биметаллическую пластинку. При нагревании такие пластинки изгибаются вследствие того, что одна расширяется больше другой. Та из полосок, которая расширяется больше, оказывается всегда с выпуклой стороны. Это свойство биметаллических пластинок широко используется для измерения температуры и её регулирования.
1. Металлический термометр. Этот прибор представляет собой биметаллическую дугу (рис. 132, а), конец которой A прочно закреплён, а конец В свободен. Дуга соединена в В со стрелкой С. При изменении температуры дуга закручивается или раскручивается, двигая соответственно стрелку. Шкала проградуирована по обыкновенному термометру. Если к концу стрелки прикрепить перо, то колебания температуры можно записывать на специальной бумажной ленте. По такому принципу устроен термограф.
2. Термостат. Так называется прибор для установления постоянной температуры.
Рас. 1326. Принцип устройства регулятора температуры с биметаллической пластинкой.
На рисунке 132б изображён принцип устройства одного из типов регуляторов температуры. Биметаллическая дуга С при изменении температуры закручивается или раскручивается. К её свободному концу прикреплена металлическая пластинка М, которая при раскручивании дуги прикасается к контакту К, а при закручивании отходит от него. Если, например, контакт К и пластинка М присоединены к концам электрической цепи АА1 содержащей нагревательный прибор, то при соприкосновении К и М электрическая цепь замкнётся; прибор начнёт нагревать помещение. Биметаллическая дуга С при нагревании начнёт закручиваться и при определённой температуре отсоединит пластинку М от контакта К цепь разорвётся, нагревание прекратится. При охлаждении дуга С, раскручиваясь, снова заставит включиться нагревательный прибор: таким образом, температура помещения будет поддерживаться на заданном уровне.
Рис. 132в. Прибор для определения коэффициента расширения жидкостей.
Тепловое расширение жидкостей
В отношении жидкостей имеет смысл говорить лишь об объёмном расширении. У жидкостей оно значительно больше, чем у твёрдых тел. Как показывает опыт, зависимость объёма жидкости от температуры выражается такой же формулой, что и для твёрдых тел.
Если при 0°С жидкость занимает объём V0, то при температуре t её объём Vt будет:
Для измерения коэффициента расширения жидкости применяется стеклянный сосуд термометрической формы, объём которого известен (рис. 132в). Шарик с трубкой наполняют доверху жидкостью и нагревают весь прибор до определённой температуры; при этом часть жидкости выливается из сосуда. Затем сосуд с жидкостью охлаждают в тающем льду до 0°. При этом жидкость наполнит уже не весь сосуд, и незаполненный объём покажет, на сколько жидкость расширилась при нагревании. Зная коэффициент расширения стекла, можно довольно точно вычислить и коэффициент расширения жидкости.
Коэффициент расширения некоторых жидкостей:
Эфир…………….0,00166 Вода (от 20°С и выше) . . . .0,00020
Спирт……………0,00110 Вода (от 5 до 8°С)…….0,00002
Керосин…………..0,00100 Ртуть…………….0,00018
Расширение воды при нагревании отличается от расширения других жидкостей. Если нагревать воду от 0°С, то можно заметить, что при нагревании до 4°С её объём не увеличивается, а уменьшается. При нагревании же выше 4°С объём воды увеличивается.
Наибольшую плотность, равную 1 
Рис. 133. График изменения плотности воды в зависимости от температуры.
Особенностью расширения воды объясняется то, что вода в прудах и озёрах не промерзает зимой до дна. При охлаждении воды осенью верхние остывшие слои опускаются на дно, а на их место снизу поступают более тёплые слои. Такое перемещение слоёв происходит только до тех пор, пока вода не примет температуру 4°С. При дальнейшем охлаждении верхние слои не опускаются вниз, а, постепенно охлаждаясь, остаются наверху и, наконец, замерзают.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно — кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
В двигателях внутреннего сгорания могут быть использованы следующие циклы:
· со смешанным подводом теплоты как при постоянном объеме, так и при постоянном давлении;
· с подводом теплоты при постоянном объеме (v = const);
· с подводом теплоты при постоянном давлении (р = const).
Во всех перечисленных циклах отвод теплоты в цикле производится при постоянном объеме в силу того, что расширение газа происходит не полностью, и степень возможного расширения в двигателе определяется положением поршня в нижней мертвой точке.
Цикл со смешанным подводом теплоты (цикл Тринклера)
Цикл со смешанным подводом теплоты (цикл Тринклера) осуществляется в бескомпрессорных дизелях. В цилиндрах дизеля сжимается чистый воздух, и происходит самовоспламенение топлива, распыление которого осуществляется механическим путем с помощью насоса или насос-форсунки под давлением 100…150 МПа.
Топливо впрыскивается в камеру сгорания или специальные предкамеры. Процесс сгорания идет вначале с повышением давления, а затем при постоянном давлении. Осуществление такого подвода теплоты характерно для двигателей, работающих по смешанному циклу. При термодинамическом исследовании рассматривают цикл, состоящий из следующих процессов (рис. 9.14): a–с – адиабатное сжатие; c–z’ – изохорный подвод теплоты; z’–z – изобарный подвод теплоты; z–e – адиабатное расширение; е–а – изохорный отвод теплоты.
Рис. 9.14. Диаграммы работы цикла со смешанным подводом теплоты
Цикл является как бы обобщающим для всех циклов поршневых ДВС. Цикл со смешанным подводом зависит от заданного начального состояния в точке с и от параметров цикла:
· степени сжатия (степень сжатия представляет собой отношение полного объема цилиндра Va к объему камеры сгорания Vc; разность между полным объемом и объемом камеры сгорания дает так называемый рабочий объем цилиндра Vh);
· степени изохорного повышения давления;
· степени предварительного (изобарного) расширения .
Параметры рабочего тела в узловых точках цикла при рассмотрении отдельных процессов, находят по формулам:
в точке с
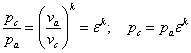
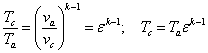
в точке
;
;
в точке
;
;
в точке е
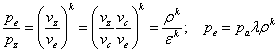
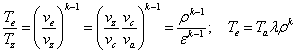
Термический КПД смешанного цикла равен:
,
где
;
;
;
.
Подставляя выражения для соответствующих температур и полагая, что теплоемкости идеального газа величины постоянные, получим:
. (9.9)
Как видно из формулы (9.9), термический КПД цикла растет с увеличением и k и уменьшается с увеличением
. Степень изохорного повышения давления
связана с величиной
. Чем больше
, тем меньше
(при тех же значениях
и q2). Тогда с ростом
термический КПД смешанного цикла увеличивается.
Работа теоретического цикла определяется по формуле:
.
Отношение работы цикла к рабочему объему vh характеризует среднее давление цикла:
.
Среднее давление смешанного цикла равно:
. (9.10)
Наиболее эффективным способом увеличения среднего давления цикла является повышение начального давления – наддув двигателя.
Рассмотренный идеальный цикл лежит в основе работы всех современных дизелей.
Цикл с подводом теплоты при постоянном объеме (цикл Отто)
Цикл с подводом теплоты при постоянном объеме (цикл Отто) является частным случаем рассмотренного цикла со смешанным подводом теплоты, когда степень изобарного расширения = 1.
По этому циклу работают двигатели, в цилиндрах которых сжимается топливно-воздушная смесь до давления 1,0… 1,5 МПа и поджигается в конце сжатия от электрической искры. Идеальный цикл Отто (рис. 9.15) состоит из процессов адиабатного сжатия (а–с), подвода к рабочему телу теплоты при v = const (c–z), адиабатного расширения (z–e) и отдачи рабочим телом теплоты при v =const (е–а).
Параметры в узловых точках цикла определяются так же, как и для цикла со смешанным подводом теплоты.
Формулы для определения и рц в этом цикле получаются из соответствующих формул для смешанного цикла при
= 1:
, (9.11)
.
Рис. 9.15. Диаграммы работы цикла с подводом теплоты при постоянном объеме
Из выражения (9.11) видно, что термический КПД цикла с подводом теплоты при v = const зависит от степени сжатия и показателя адиабаты k рабочего тела, совершающего цикл. Несмотря на то, что с увеличением степени сжатия растут термический КПД и полезная работа цикла, при больших степенях сжатия ( > 10) в результате значительного повышения температуры в конце процесса сжатия может наступить самовоспламенение смеси.
Еще более существенным является то обстоятельство, что с увеличением степени сжатия, а следовательно, и с увеличением температуры в конце сжатия появляется детонация свежей рабочей смеси, которая приводит к взрывному характеру сгорания. В результате детонации процесс сгорания нарушается, мощность двигателя падает, расход топлива растет. По этой причине двигатели, работающие по циклу v = const, имеют вполне определенные предельные значения степени сжатия ( = 5,5…9,0).
Явление детонации в значительной степени зависит от сорта применяемого топлива, от его антидетонационных качеств. Поэтому сорт применяемого топлива определяет выбор предельного значения степени сжатия для двигателей легкого топлива.
Цикл с подводом теплоты при постоянном давлении (цикл Дизеля)
Цикл с подводом теплоты при постоянном давлении (цикл Дизеля) является также частным случаем обобщающего цикла при = 1. В двигателях дизеля раздельно сжимается воздух до давления 4,0…5,0 МПа, и смесь топлива с воздухом, сжатым во вспомогательном компрессоре. Подача топлива осуществляется так, чтобы давление в процессе сгорания оставалось постоянным.
Идеальный цикл дизеля (рис. 9.16) состоит из двух адиабат сжатия и расширения, изобары подвода теплоты и изохоры отвода теплоты Термический КПД и среднее давление цикла из формул (9.9) и (9.10) при = 1 соответственно равны:
, (9.12)
.
Влияние на
такое же, как и в циклах Тринклера и Отто, т.е. с увеличением степени сжатия увеличивается и термический КПД цикла. При увеличении степени предварительного расширения (
), как видно из формулы (9.12), термический КПД цикла должен падать.
Рис. 9.16. Диаграммы работы цикла с подводом теплоты при постоянном давлении
При постоянной степени сжатия увеличение вызовет увеличение объема vz , который зависит от подводимого количества теплоты q1. При увеличении q1 увеличивается объем vz, а вместе с ним увеличивается и работа цикла. Таким образом, возрастание
приводит к увеличению работы и уменьшению термического КПД.
Сопоставляя значения термических КПД циклов с подводом теплоты при v = const и p = const, видим, что они различаются множителем:
.
Отсюда следует, что при одинаковых степенях сжатия >
.
Термодинамическая эффективность каждого из рассмотренных циклов зависит от конкретных условий его осуществления. Целесообразнее сравнивать циклы при различных степенях сжатия , но при одинаковых максимальных давлениях и температурах и одинаковом отведенном количестве теплоты q2.
Из TS-диаграммы (рис. 9.17) следует, что наибольший термический КПД будет у цикла с подводом теплоты при р = const:
>
>
.
КПД смешанного цикла имеет промежуточное значение по сравнению с циклами с подводом теплоты при p = const и v = const.
Рис. 9.17. Сравнение циклов при различных степенях сжатия
При оптимальных степенях сжатия (для цикла Отто < 10, для цикла Дизеля
= 16 и для смешанного
= 22):
= 3,2…4,2;
= 1,6…2,0;
= 1,3…1,7,
,
что видно из рис. 9.18. Поэтому все выпускаемые сейчас дизели работают по смешанному циклу.
Рис. 9.18. Диаграмма работы циклов при оптимальных степенях сжатия