Как найти вероятность из графиков плотности вероятности
Перевод
Ссылка на автора
Прежде чем идти дальше, давайте посмотрим правде в глаза.
Если вы достаточно давно работаете в области наук о данных, есть вероятность, что вы, возможно, построили графики плотности вероятности (аналогичные приведенным ниже), чтобы понять общее распределение ваших данных.
Ну … Во-первых, что за график плотности? Отличное и ясное объяснение Уилл Кёрсен это:
график плотности является сглаженной, непрерывной версией гистограммы, оцененной по данным.
Наиболее распространенная форма оценки известна как оценка плотности ядра (KDE).
В этом методе непрерывная кривая (ядро) рисуется в каждой отдельной точке данных, и все эти кривые затем складываются, чтобы сделать единую плавную оценку плотности.
Ядро, наиболее часто используемоеGaussian(который создает гауссову кривую колокола в каждой точке данных)
график плотности вероятностипросто означает график плотности функции плотности вероятности (ось Y) против точек данных переменной (ось X).
Как правило, графики плотности вероятности используются дляпонимать распределение данныхдля непрерывной переменной, и мы хотимзнать вероятность (или вероятность) получения диапазона значенийчто непрерывная переменная может принять.
Но вот в чем дело.
Показывая графики плотности вероятности, мы можем понять только распределение данных.визуальноне зная точную вероятность для определенного диапазона значений.
Другими словами, трудно оценить количественно вероятность под кривой, просто посмотрев на график.
Однако получение точной вероятности под кривойчрезвычайно важно(Я расскажу вам почему в следующем разделе), особенно когда вы представляете заинтересованным сторонам бизнеса.
В этой статье я покажу вам полный код, который я использовал для вычисления вероятности, и объясню вам шаг за шагом, как вы можете это сделать.
К концу этой статьи, я надеюсь, вы лучше поймете распределение данных, рассчитав фактическую вероятность в пределах диапазона значений, и впоследствии сможете убедить заинтересованные стороны в ваших взглядах.
Вы можете получить набор данных и блокнот Jupyter от моего GitHub,
Давайте начнем!
Почему графики плотности вероятности недостаточно убедительны?
Оглядываясь на график плотности выше, вы, возможно, пришли к выводу, что рейсы авиакомпании Alaska Airlines выполняются раньше, чем United Airlines.
Представьте, что теперь ваш босс задает этот вопрос и оспаривает ваше утверждение,«Как раньше сравниваются рейсы авиакомпании Alaska Airlines с United Airlines и насколько высоки шансы на это? У вас есть какие-либо числовые доказательства того, что ваш вывод верен?
Вы ошеломлены. Потому что вывод приходит из вашего наблюдения за общим распределением данных.
Что еще хуже, теперь у вас нет никаких числовых доказательств — точной вероятности — в поддержку вашего заявления.
Вы не очень хорошо подготовлены, и ваш авторитет в качестве ученого по данным мгновенно развалится, если вы не сможете доказать свою точку зрения.
Вот тут и возникает важность вычисления вероятности по графикам плотности вероятности.
К сожалению, очень трудно рассчитать вероятность, если вы используете Seaborn для построения графиков плотности, используяdistplot,
Потратив некоторое трудное время на выяснение того, как рассчитать вероятность, я решил использоватьKernelDensityотsklearn,
Этот метод работает как шарм, и я очень рад поделиться этим с вами! 👇🏻
Вот как найти вероятность из графиков плотности вероятности
Мы будем использовать данные о чаевых, которые включают некоторые факторы, которые могут повлиять на количество чаевых, которые дают клиенты в ресторане. Вы можете получить данные Вот,
Поскольку наша цель здесь — найти вероятность по графикам плотности, чтобы упростить ее, мы сосредоточимся на ответе на один вопрос —Клиенты дают больше советов во время обеда / ужина?
Поскольку данные уже достаточно очищены, мы можем начать строить графики плотности и напрямую вычислять соответствующие значения вероятности.
Для следующих шагов, пожалуйста, обратитесь к блокнот для полной реализации кода с использованием функций.
1. Составьте графики плотности вероятности
Поскольку Seaborn не предоставляет каких-либо функциональных возможностей для вычисления вероятности из KDE, таким образом, код выполняет эти 3 шага (как показано ниже) для построения графиков плотности вероятности и вывода объектов KDE для последующего расчета вероятности.
- График нормализованных гистограмм
- Выполнить оценку плотности ядра (KDE)
- Плотность вероятности заговора
Теперь, когда у нас есть график плотности вероятности количества советов на обед и ужин, время для сравнения
Просто взглянув на диапазон от 1 до 3 долларов советов, данных клиентами, мы можем заключить, чтоклиенты обычно дают чаевые 1-3 доллара в обеденное время по сравнению с обедом
Опять же, для того, чтобы получить числовые доказательства (или вероятностные значения), подкрепляющие наше утверждение, давайте посчитаем вероятность того, что клиенты дадут чаевые в размере 1–3 доллара США во время обеда и ужина для сравнения.
2. Рассчитать вероятность
Как только мы сделали графики плотности вероятности с помощью функцииplot_prob_densityу нас будут выходные объекты KDE из этой функции в качестве входных данных для вычисления вероятности с использованием следующей функции —get_probability,
И вот оно!
Сумма вероятности под нормализованной кривой плотности всегда равна 1. Поскольку вероятность — это область под кривой, мы можем затем указать диапазон значений (в данном случае чаевые от 1 до 3 долларов США) для расчета вероятности в этом диапазоне.
Следовательно, вероятность — это просто умножение значений плотности вероятности (ось Y) и количества подсказок (ось X).
Умножение выполняется для каждой точки оценки, и эти умноженные значения затем суммируются для вычисления окончательной вероятности.
Рассчитанные вероятности подтверждают нашу первоначальную претензию — клиенты обычно дают чаевые в размере 1–3 долл. Во время обеда по сравнению с обедомс вероятностью 63% более 49%.
Последние мысли
Спасибо за чтение.
Я надеюсь, что эта статья дает вамлучшее понимание графиков плотности вероятностии самое главное, показывает, какрассчитать фактическую вероятность в диапазоне значенийпод кривой плотности вероятности.
Расчет вероятности довольно прост, но не тривиален. Это играет решающую роль длядать заинтересованным сторонам лучшее понимание ваших графиков плотности вероятности, чтобы придумать действенные идеи, основанные на численных доказательствахвместо субъективного и неоднозначного наблюдения.
Как всегда, если у вас есть какие-либо вопросы или комментарии, не стесняйтесь оставлять свои отзывы ниже, или вы всегда можете связаться со мной по LinkedIn, До тех пор, до встречи в следующем посте! 😄
об авторе
Адмонд ли известен как один из самых востребованныхученые-данные и консультантыпомогая основателям стартапов и различным компаниям решать их проблемы, используя данные с большим опытом вконсалтинг по науке о данных и знание отрасли,
Вы можете связаться с ним на LinkedIn, средний, щебет, а также facebook или забронировать встречу с ним здесь если вы ищете консалтинга для вашей компании.
Бронируйте онлайн с Admond Lee
Адмонд Ли известен как один из самых востребованных ученых и консультантов в области данных, помогающий начинающим основателям и…
bit.ly
Справочник ОГЭ по математике. Раздел 8. Статистика и теория вероятностей
На ОГЭ по математике по данному разделу необходимо знать:
- что такое статические таблицы, таблицы, диаграммы, графики;
- основные вероятностные понятия;
- средние результаты измерений;
- события;
- частота событий;
- геометрическая вероятность;
- понятие события, частоты события, геометрической вероятности;
- основные комбинаторные правила.
На ОГЭ по математике по данному разделу необходимо уметь:
- извлекать статистическую информацию, представленную в таблицах, на диаграммах, графиках;
- решать комбинаторные задачи путем организованного перебора вариантов, а также с использованием правила умножения;
- вычислять средние результаты измерений;
- находить частоту события, используя собственные наблюдения и готовые статистические данные;
- находить вероятности случайных событий в простейших случаях.
ОГЛАВЛЕНИЕ Перейти в другие разделы: 7.6 … 1.1
8. Статистика и теория вероятностей
8.1. Описательная статистика.
8.1.1. Представление данных в виде
таблиц, диаграмм, графиков.
8.1.2. Среднее результатов измерений.
8.2. Вероятность.
8.2.1. Частота события, вероятность.
8.2.2. Равновозможные события
и подсчет их вероятности.
8.2.3. Представление о геометрической вероятности.
8.3. Комбинаторика
8.3.1. Решение комбинаторных задач:
перебор вариантов, комбинаторное правило умножения.
Вы смотрели конспект по математике «8. Статистика и теория вероятностей (справочник ОГЭ)»:
- 8.1. Описательная статистика.
- 8.1.1. Представление данных в виде таблиц, диаграмм, графиков.
- 8.1.2. Среднее результатов измерений.
- 8.2. Вероятность.
- 8.2.1. Частота события, вероятность.
- 8.2.2. Равновозможные события и подсчет их вероятности.
- 8.2.3. Представление о геометрической вероятности.
- 8.3. Комбинаторика.
8.3.1. Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения.
Выберите дальнейшее действие:
-
Перейти в Кодификатор ОГЭ по математике
-
Перейти к Оглавлению Справочника ОГЭ по математике (Третьяк И.В.)
-
Купить Справочник ОГЭ по математике (Третьяк И.В.)
Нормальное распределение: понимание гистограмм и вероятностей
Добавлено 14 августа 2020 в 19:41
В данной статье мы продолжаем исследование нормального распределения, рассматривая концепцию гистограмм и вводя функцию массы вероятности.
Данная статья является частью серии статей о статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики. Затем мы исследовали три описательных статистических показателя с точки зрения применения в обработке сигналов.
Затем мы коснулись стандартного отклонения (в частности, определения компенсации размера выборки при вычислении стандартного отклонения и понимания взаимосвязи между стандартным отклонением и среднеквадратичным значением).
В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего текущего обсуждения: понимание вероятностей в измеренных данных.
Понимание гистограмм
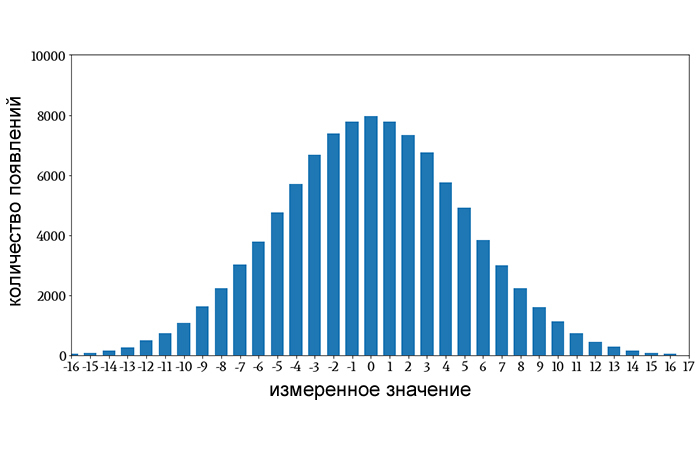
В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:
Я думаю, что большинство людей, работающих в области науки или техники, хотя бы смутно знакомы с гистограммами, но давайте сделаем шаг назад.
Что такое гистограмма?
Гистограммы – это визуальные представления 1) значений, присутствующих в наборе данных, и 2) частоты появления этих значений. Показанная выше гистограмма может представлять множество различных типов информации.
Представим, что она представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного стабилизатора, который подвергался различным температурам и условиям эксплуатации. Так, например, примерно 8000 измерений показали разницу в 0 мВ между номинальным и фактическим выходными напряжениями, а примерно 1000 измерений показали разницу в 10 мВ.
Гистограммы – чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.
Гистограммы с интервалами
Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем объединение в интервалы (биннинг). То есть мы определяем диапазон значений как интервал, группируем результаты измерений в эти интервалы и создаем по одному столбцу для каждого интервала.
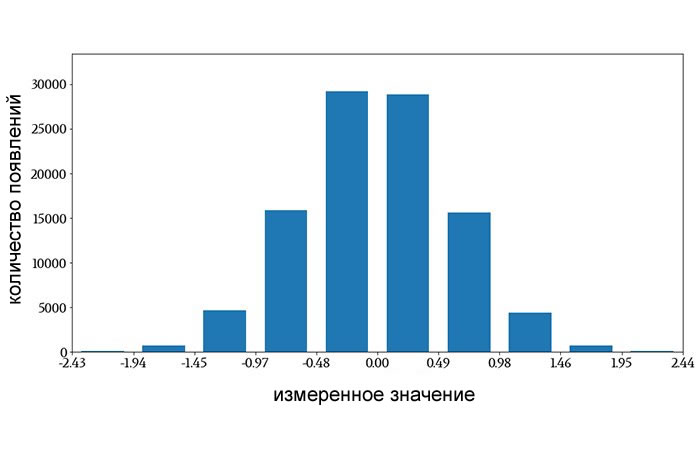
Следующая гистограмма, которая была сгенерирована из нормально распределенных данных со средним значением 0 и стандартным отклонением 0,6, использует интервалы вместо отдельных значений:
Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначен один столбец. Все результаты измерений, попадающие в числовой интервал, влияют на высоту соответствующего столбца (метки на горизонтальной оси показывают, что интервалы не одинаковой ширины, но это просто потому, что значения меток округлены).
Гистограммы и вероятность
В некоторых ситуациях гистограмма не дает нужной нам информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но не можем легко определить вероятность измеренного значения.
Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжениями стабилизатора, но я не знаю, какова вероятность того, что результат случайно выбранного измерения или нового измерения сообщит о разнице в 0 В.
Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: каковы шансы, что…?
Каковы шансы, что у моего линейного стабилизатора погрешность выходного напряжения будет менее 2 мВ? Какова вероятность того, что частота битовых ошибок моего канала передачи данных будет выше 10-3? Какова вероятность того, что из-за шума мой входной сигнал превысит порог срабатывания? И так далее.
Причина этого ограничения заключается в том, что гистограмма просто четко не передает размер выборки, то есть общее количество измерений (теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно).
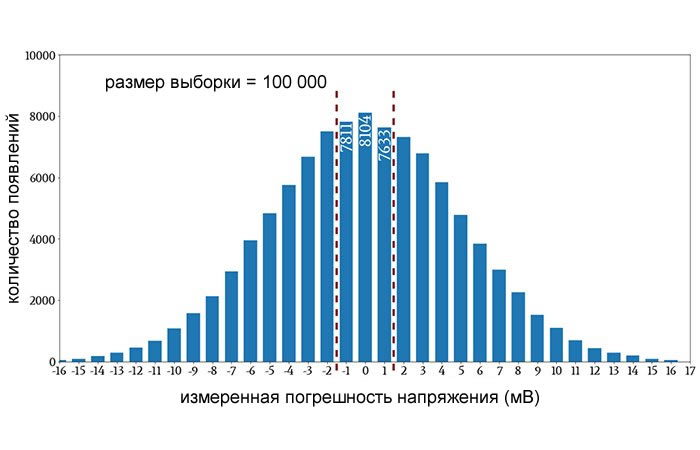
Если мы знаем размер выборки, мы можем разделить количество появлений на размер выборки и таким образом определить вероятность. Давайте рассмотрим пример.
Красные пунктирные линии заключают в себя столбцы, которые указывают на погрешности напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех значений погрешности напряжения. Сумма этих трех чисел составляет 23 548. Таким образом, на основе этого примера по сбору данных вероятность получения погрешности менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.
Функция массы вероятности
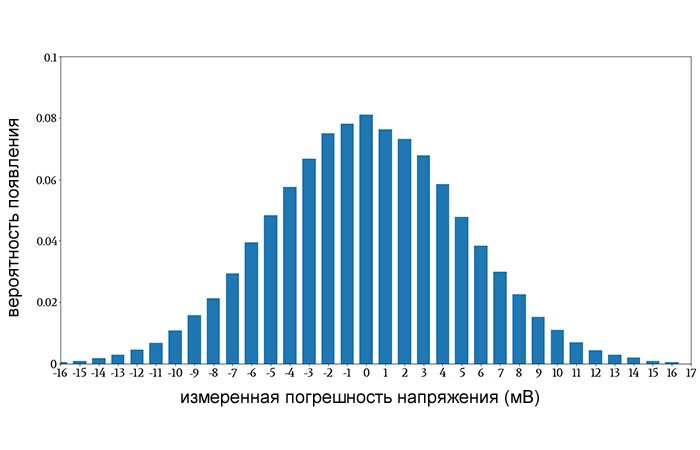
Если наша основная цель при создании гистограммы – передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все счетчики вхождений на размер выборки.
Полученный график является аппроксимацией функции массы вероятности. Например:
Всё, что мы на самом деле выполнили, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или на группу значений и легко определить вероятность появления.
Хочу прояснить следующую деталь: я сказал, что мы аппроксимируем функцию массы вероятности, когда берем гистограмму и делим значения на размер выборки. Истинная функция массы вероятности представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.
Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе измеренных данных, дает нам только приближение функции массы вероятности.
Масса вероятности против плотности вероятности
Стоит подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (о которой мы говорили в предыдущей статье).
В то время как функция плотности вероятности является непрерывной и предоставляет значения вероятности, когда мы интегрируем функцию в указанном диапазоне, функция массы вероятности дискретизируется и дает нам вероятность, связанную с конкретным значением или интервалом.
Эти две функции передают одну и ту же общую статистическую информацию о переменной или о сигнале, но делают это по-разному.
Обратите внимание на разницу между двумя названиями: вертикальная ось функции массы вероятности указывает массу вероятности, как количественное значение. Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; чтобы определить количественное значение вероятности, мы должны интегрировать эту плотность по горизонтальной оси.
Заключение
Мы рассмотрели функции массы и плотности вероятности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.
Теги
ГистограммаМасса вероятностиНормальное распределение / Гауссово распределениеПлотность вероятностиСтатистикаФункция массы вероятностиФункция плотности вероятности
Время на прочтение
11 мин
Количество просмотров 109K
У data scientist-ов сотни распределений вероятности на любой вкус. С чего начать?
Data science, чем бы она там не была – та ещё штука. От какого-нибудь гуру на ваших сходках или хакатонах можно услышать:«Data scientist разбирается в статистике лучше, чем любой программист». Прикладные математики так мстят за то, что статистика уже не так на слуху, как в золотые 20е. У них даже по этому поводу есть своя несмешная диаграмма Венна. И вот, значит, внезапно вы, программист, оказываетесь совершенно не у дел в беседе о доверительных интервалах, вместо того, чтобы привычно ворчать на аналитиков, которые никогда не слышали о проекте Apache Bikeshed, чтобы распределённо форматировать комментарии. Для такой ситуации, чтобы быть в струе и снова стать душой компании – вам нужен экспресс-курс по статистике. Может, не достаточно глубокий, чтобы вы всё понимали, но вполне достаточный, чтобы так могло показаться на первый взгляд.
Вероятностные распределения – это основа статистики, так же как структуры данных – основа computer science. Если хотите говорить языком data scientist-а – надо начинать с их изучения. В принципе можно, если повезёт, делать простые анализы, используя R или scikit-learn вообще без понимания распределений, так же как можно написать программу на Java без понимания хэшфункций. Но рано или поздно это закончится слезами, ошибками, ложными результатами или — гораздо хуже – охами и выпученными глазами от старших статистиков.
Существуют сотни различных распределений, некоторые из которых на слух звучат как чудовища средневековых легенд, типа Muth или Lomax. Тем не менее, на практике более-менее часто используются около 15. Каковы они, и какие умные фразы о них требуется запомнить?
Итак, что такое распределение вероятности?
Всё время что-то происходит: кидаются кубики, идёт дождь, подъезжают автобусы. После того, как это что-то произошло, можно быть уверенным в некотором исходе: кубики выпали на 3 и 4, выпало 2.5 см дождя, автобус подъехал через 3 минуты. Но до этого момента мы можем говорить только о том, насколько каждый исход возможен. Распределения вероятности описывают то, как мы видим вероятность каждого исхода, что, зачастую, гораздо интереснее, чем знать только один, наиболее возможный, исход. Распределения бывают разных форм, но строго одного размера: сумма всех вероятностей в распределении — всегда 1.
Например, подбрасывание правильной монетки имеет два исхода: она упадёт либо орлом, либо решкой (предполагая, что она не приземлится на ребро и её не стащит в воздухе чайка). Перед броском мы верим, что с шансом 1 к 2 или с вероятностью 0.5 она упадёт орлом. Точно так же, как и решкой. Это распределение вероятности двух исходов броска, и, если вы внимательно прочитали это предложение, то вы уже поняли распределение Бернулли.
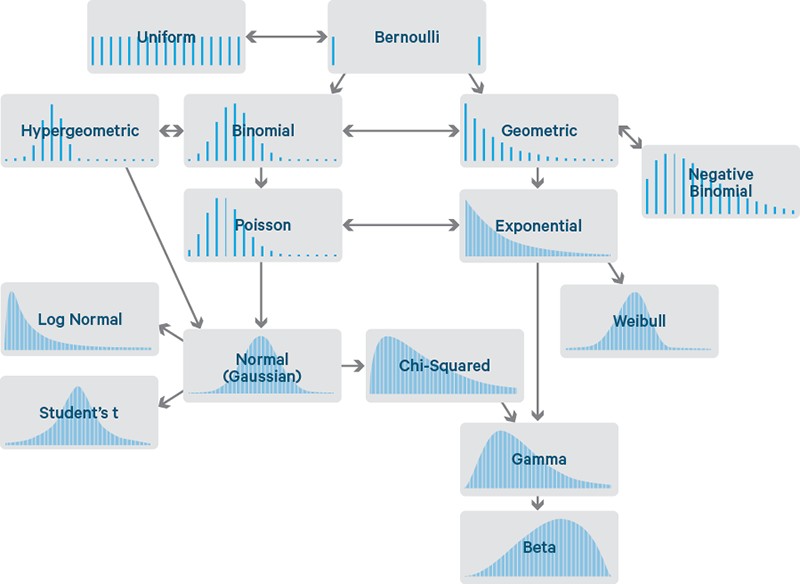
Несмотря на экзотические названия, распространённые распределения связаны друг с другом достаточно интуитивными и интересными способами, позволяющими легко их вспоминать и уверенно о них рассуждать. Некоторые естественно следуют, например, из распределения Бернулли. Время показать карту этих связей.
Каждое распределение иллюстрируется примером её функции плотности распределения (ФПР). Эта статья только о тех распределениях, у которых исходы – одиночные числа. Поэтому, горизонтальная ось каждого графика – набор возможных чисел-исходов. Вертикальная – вероятность каждого исхода. Некоторые распределения дискретны — у них исходы должны быть целыми числами, типа 0 или 5. Таковые обозначаются редкими линиями, по одной на каждый исход, с высотой, соответствующей вероятности данного исхода. Некоторые – непрерывны, у них исходы могут принять любое численное значение, типа -1.32 или 0.005. Эти показаны плотными кривыми с областями под секциями кривой, которые дают вероятности. Сумма высот линий и областей под кривыми — всегда 1.
Распечатайте, отрежьте по пунктирной линии и носите с собой в кошельке. Это — ваш путеводитель в стране распределений и их родственников.
Бернулли и равномерное
Вы уже встретились с распределением Бернулли выше, с двумя исходами – орлом или решкой. Представьте его теперь как распределение над 0 и 1, 0 – орёл, 1 – решка. Как уже понятно, оба исхода равновероятны, и это отражено на диаграмме. ФПР Бернулли содержит две линии одинаковой высоты, представляющие 2 равновероятных исхода: 0 и 1 соответственно.
Распределение Бернулли может представлять и неравновероятные исходы, типа броска неправильной монетки. Тогда вероятность орла будет не 0.5, а какая-то другая величина p, а вероятность решки – 1-p. Как и многие другие распределения, это на самом деле целое семейство распределений, задаваемых определёнными параметрами, как p выше. Когда будете думать «Бернулли» – думайте про «бросок (возможно, неправильной) монетки».
Отсюда весьма небольшой шаг до того, чтобы представить распределение поверх нескольких равновероятных исходов: равномерное распределение, характеризуемое плоской ФПР. Представьте правильный игральный кубик. Его исходы 1-6 равновероятны. Его можно задать для любого количества исходов n, и даже в виде непрерывного распределения.
Думайте о равномерном распределении как о «правильном игральном кубике».
Биномиальное и гипергеометрическое
Биномиальное распределение можно представить как сумму исходов тех вещей, которые следуют распределению Бернулли.
Киньте честную монету два раза – сколько раз будет орёл? Это число, подчиняющееся биномиальному распределению. Его параметры – n, число испытаний, и p – вероятность «успеха» (в нашем случае – орла или 1). Каждый бросок – распределённый по Бернулли исход, или испытание. Используйте биномиальное распределение, когда считаете количество успехов в вещах типа броска монеты, где каждый бросок не зависит от других и имеет одинаковую вероятность успеха.
Или представьте урну с одинаковым количество белых и чёрных шаров. Закройте глаза, вытащите шар, запишите его цвет и верните назад. Повторите. Сколько раз вытащился чёрный шар? Это число также подчиняется биномиальному распределению.
Эту странную ситуацию мы представили, чтобы было легче понять смысл гипергеометрического распределения. Это распределение того же числа, но в ситуации если бы мы не возвращали шары обратно. Оно, безусловно, двоюродный брат биномиального распределения, но не такое же, так как вероятность успеха изменяется с каждым вытащенным шаром. Если количество шаров достаточно велико по сравнению с количеством вытаскиваний – то эти распределения практически одинаковы, так как шанс успеха изменяется с каждым вытаскиванием крайне незначительно.
Когда где-то говорят о вытаскивании шаров из урн без возврата, практически всегда безопасно ввернуть «да, гипергеометрическое распределение», потому что в жизни я ещё не встречал никого, кто реально наполнял бы урны шарами и потом вытаскивал их и возвращал, или наоборот. У меня даже знакомых нет с урнами. Ещё чаще это распределение должно всплывать при выборе значимого подмножества некоторой генеральной совокупности в качестве выборки.
Прим. перев.
Тут может быть не очень понятно, а раз туториал и экспресс-курс для новичков — надо бы разъяснить. Генеральная совокупность — есть нечто, что мы хотим статистически оценить. Для оценки мы выбираем некоторую часть (подмножество) и производим требуемую оценку на ней (тогда это подмножество называется выборкой), предполагая, что для всей совокупности оценка будет похожей. Но чтобы это было верно, часто требуются дополнительные ограничения на определение подмножества выборки (или наоборот, по известной выборке нам надо оценить, описывает ли она достаточно точно совокупность).
Практический пример — нам нужно выбрать от компании в 100 человек представителей для поездки на E3. Известно, что в ней 10 человек уже ездили в прошлом году (но никто не признаётся). Сколько минимум нужно взять, чтобы в группе с большой вероятностью оказался хотя бы один опытный товарищ? В данном случае генеральная совокупность — 100, выборка — 10, требования к выборке — хотя бы один, уже ездивший на E3.
В википедии есть менее забавный, но более практичный пример про бракованные детали в партии.
Пуассон
Что насчёт количества заказчиков, звонящих по горячей линии в техподдержку каждую минуту? Это исход, чьё распределение на первый взгляд биномиальное, если считать каждую секунду как испытание Бернулли, в течение которой заказчик либо не позвонит (0), либо позвонит (1). Но электроснабжающие организации прекрасно знают: когда выключают электричество – за секунду могут позвонить двое или даже больше сотни людей. Представить это как 60000 миллисекундных испытаний тоже не поможет – испытаний больше, вероятность звонка в миллисекунду меньше, даже если не учитывать двух и более одновременно, но, технически – это всё ещё не испытание Бернулли. Тем не менее, срабатывает логическое рассуждение с переходом к бесконечности. Пусть n стремится к бесконечности, а p – к 0, и так, чтобы np было постоянным. Это как делить на всё более малые доли времени со всё менее малой вероятностью звонка. В пределе мы получим распределение Пуассона.
Так же, как и биномиальное, распределение Пуассона – это распределение количества: количества раз того, как что-то произойдёт. Оно параметризуется не вероятностью p и количеством испытаний n, но средней интенсивностью λ, что, в аналогии с биномиальным, просто постоянное значение np. Распределение Пуассона – то, о чём надо вспоминать, когда идёт речь о подсчёте событий за определённое время при постоянной заданной интенсивности.
Когда есть что-то, типа прихода пакетов на роутер или появления покупателей в магазине или что-то, ожидающее в очереди – думайте «Пуассон».
Прим. перев.
Я бы месте автора я рассказал про отсутствие памяти у Пуассона и Бернулли (распределений, а не людей) и предложил бы в разговоре ввернуть что-нибудь умное про парадокс закона больших чисел как его следствие.
Геометрическое и отрицательное биномиальное
Из простых испытаний Бернулли появляется другое распределение. Сколько раз монетка выпадет решкой, прежде, чем выпасть орлом? Число решек подчиняется геометрическому распределению. Как и распределение Бернулли, оно параметризуется вероятностью успешного исхода, p. Оно не параметризуется числом n, количеством бросков-испытаний, потому что число неудачных испытаний как раз и есть исход.
Если биномиальное распределение это «сколько успехов», то геометрическое это «Сколько неудач до успеха?».
Отрицательное биномиальное распределение – простое обобщение предыдущего. Это количество неудач до того, как будет r, а не 1, успехов. Поэтому оно дополнительно параметризуется этим r. Иногда его описывают как число успехов до r неудач. Но, как говорит мой лайф-коуч: «Ты сам решаешь, что есть успех, а что — неудача», так что это тоже самое, если при этом не забыть, что вероятность p тоже должна правильной вероятностью успеха или неудачи соответственно.
Если нужна будет шутка для снятия напряжения, можно упомянуть, что биномиальное и гипергеометрическое распределение – это очевидная пара, но и геометрическое и отрицательное биномиальное так же весьма похожи, после чего заявить «Ну и кто же так их все называет, а?»
Экспоненциальное и Вейбула
Снова о звонках в техподдержку: сколько пройдёт до следующего звонка? Распределение этого времени ожидания как будто бы геометрическое, потому что каждая секунда, пока никто не звонит – это как неуспех, до секунды, пока, наконец, звонок не произойдёт. Количество неудач –это как количество секунд, пока никто не звонил, и это практически время до следующего звонка, но «практически» нам недостаточно. Суть в том, что это время будет суммой целых секунд, и, таким образом, не получится посчитать ожидание внутри этой секунды до непосредственно звонка.
Ну и, как и раньше, переходим в геометрическом распределении к пределу, относительно временных долей – и вуаля. Получаем экспоненциальное распределение, которое точно описывает время до звонка. Это непрерывное распределение, первое такое у нас, потому что исход не обязательно в целых секундах. Как и распределение Пуассона, оно параметризуется интенсивностью λ.
Повторяя связь биномиального с геометрическим, Пуассоновское «сколько событий за время?» связано с экспоненциальным «сколько до события?». Если есть события, количество которых на единицу времени подчиняется распределению Пуассона, то время между ними подчиняется экспоненциальному распределению с тем же параметром λ. Это соответствие между двумя распределениями необходимо отмечать, когда обсуждается любое из них.
Экспоненциальное распределение должно приходить на ум при размышлении о «времени до события», возможно, «времени до отказа». По факту, это такая важная ситуация, что существуют более обобщённые распределения чтобы описать наработку-на-отказ, типа распределения Вейбула. В то время, как экспоненциальное распределение подходит, когда интенсивность — износа, или отказов, например – постоянна, распределение Вейбула может моделировать увеличивающуюся (или уменьшающуюся) со временем интенсивность отказов. Экспоненциальное, в общем-то, частный случай.
Думайте «Вейбул» когда разговор заходит о наработке-на-отказ.
Нормальное, логнормальное, Стьюдента и хи-квадрат
Нормальное, или гауссово, распределение, наверное, одно из важнейших. Его колоколообразная форма узнаётся сразу. Как и e, это особенно любопытная сущность, которая проявляется везде, даже из внешне самых простых источников. Возьмите набор значений, подчиняющихся одному распределению – любому! – и сложите их. Распределение их суммы подчиняется (приблизительно) нормальному распределению. Чем больше вещей суммируется – тем ближе их сумма соответствует нормальному распределению (подвох: распределение слагаемых должно быть предсказуемым, быть независимым, оно стремится только к нормальному). То, что это так, несмотря на исходное распределение – это потрясающе.
Прим. перев.
Меня удивило, что автор не пишет про необходимость сопоставимого масштаба суммируемых распределений: если одно существенно доминирует надо остальными — сходиться будет крайне плохо. И, в общем-то, абсолютная взаимная независимость необязательна, достаточна слабая зависимость.
Ну сойдёт, наверное, для вечеринок, как он написал.
Это называется «центральная предельная теорема», и надо знать, что это, почему так названо и что означает, иначе моментально засмеют.
В её разрезе, нормальное связано со всеми распределениями. Хотя, в основном, его связывают с распределениями всяких сумм. Сумма испытаний Бернулли следует биномиальному распределению и, с увеличением количества испытаний, это биномиальное распределение становится всё ближе в нормальному распределению. Аналогично и его двоюродный брат – гипергеометрическое распределение. Распределение Пуассона – предельная форма биномиального – так же приближается к нормальному с увеличением параметра интенсивности.
Исходы, которые подчиняются логнормальному распределению, дают значения, логарифм которых нормально распределён. Или по-другому: экспонента нормально распределённого значения логнормально распределена. Если суммы – нормально распределены, то запомните так же, что произведения распределены логнормально.
t-Распределение Стьюдента – это основа t-теста, который многие нестатистики изучают в других областях. Оно используется для предположений о среднем нормального распределения и так же стремится к нормальному распределению с увеличением своего параметра. Отличительная особенность t-распределения – его хвосты, которые толще, чем у нормального распределения.
Если толстохвостый анекдот недостаточно раскачал вашего соседа – переходите в довольно забавной байке про пиво. Больше 100 лет назад Гиннесс использовал статистику, чтобы улучшить свой стаут. Тогда Вильям Сили Госсет и изобрёл полностью новую статистическую теорию для улучшенного выращивания ячменя. Госсет убедил босса, что другие пивовары не поймут, как использовать его идеи, и получил разрешение на публикацию, но под псевдонимом «Стьюдент». Самое известное достижение Госсета – как раз это самое t-распределение, которое, можно сказать, названо в честь него.
Наконец, распределение хи-квадрат – распределение сумм квадратов нормально-распределенных величин. На этом распределении построен тест хи-квадрат, который сам основан на сумме квадратов разниц, которые должны быть нормально распределены.
Гамма и бета
В этом месте, если вы уже заговорили о чём-то хи-квадратном, разговор начинается всерьёз. Вы уже, возможно, говорите с настоящими статистиками, и, наверное, стоит уже откланиваться, поскольку могут всплыть вещи типа гамма-распределения. Это обобщение и экспоненциального, и хи-квадрат распределения. Как и экспоненциальное распределение, оно используется для сложных моделей времен ожидания. Например, гамма-распределение появляется, когда моделируется время до следующих n событий. Оно появляется в машинном обучении как «сопряжённое априорное распределение» к парочке других распределений.
Не вступайте в разговор об этих сопряжённых распределениях, но если всё-таки придётся, не забудьте сказать о бета-распределении, потому что оно сопряжённое априорное к большинству упомянутых здесь распределений. Data-scientist-ы уверены, что оно именно для этого и сделано. Упомяните об этом ненароком и идите к двери.
Начало мудрости
Распределения вероятности — это то, о чём нельзя знать слишком много. По настоящему заинтересованные могут обратиться к этой супердетализированной карте всех распределений вероятности. Надеюсь, этот шуточный путеводитель даст вам уверенность казаться «в теме» в современной технокультуре. Или, по крайней мере, способ с высокой вероятностью определить, когда надо идти на менее ботанскую вечеринку.
Шон Овен – директор Data Science в Cloudera, Лондон. До Клаудеры он основал Myrrix Ltd. (сейчас проект Oryx) для коммерционализации широкомасштабных рекомендательных систем в реальном времени на Hadoop. Он так же контрибьютор Apache Spark и соавтор O’Reilly Media’s Advanced Analytics with Spark
Как использовать древовидную диаграмму для определения вероятности
На чтение 3 мин. Просмотров 41 Опубликовано 15.07.2021
Древовидные диаграммы – полезный инструмент для вычисления вероятностей, когда задействовано несколько независимых событий. Они получили свое название потому, что эти типы диаграмм напоминают форму дерева. Ветви дерева отделяются друг от друга, и они, в свою очередь, имеют более мелкие ветви. Как и дерево, древовидные диаграммы разветвляются и могут стать довольно сложными.
Если мы подбрасываем монету, предполагая, что монета справедливая, то вероятность выпадения орла и решки одинакова. Поскольку это единственные два возможных исхода, каждый имеет вероятность 1/2 или 50 процентов. Что произойдет, если мы подбросим две монеты? Каковы возможные результаты и вероятности? Мы увидим, как использовать древовидную диаграмму, чтобы ответить на эти вопросы.
Прежде чем мы начнем, мы должны отметить, что то, что происходит с каждой монетой, не влияет на результат другой. Мы говорим, что эти события независимы друг от друга. В результате не имеет значения, подбрасываем ли мы сразу две монеты или одну монету, а затем другую. На древовидной диаграмме мы рассмотрим оба подбрасывания монеты по отдельности.
Содержание
- Первый бросок
- Второй бросок
- Расчет вероятностей
Первый бросок

Здесь мы проиллюстрируем первое подбрасывание монеты. На схеме “голова” обозначается аббревиатурой “H”, а “T” – буквой “T”. Оба этих исхода имеют вероятность 50 процентов. На схеме это показано двумя разветвленными линиями. Важно записывать вероятности на ветвях диаграммы по мере продвижения. Мы немного увидим почему.
Второй бросок

Теперь мы видим результаты второго подбрасывания монеты. Если при первом броске выпадет орел, каковы возможные результаты второго броска? На второй монете может быть орел или решка. Аналогичным образом, если решка выпадет первой, то при втором броске может выпасть орел или решка. Мы представляем всю эту информацию, отрисовывая ветви второго подбрасывания монеты от обеих ветвей от первого подбрасывания. Вероятности снова назначаются каждому ребру.
Расчет вероятностей

Теперь мы читаем нашу диаграмму слева, чтобы написать и сделать две вещи:
- Следуем каждому пути и записываем результаты.
- Следуем каждому пути и умножаем вероятности.
Причина, по которой мы умножаем вероятности, заключается в том, что у нас есть независимые события. Мы используем правило умножения для выполнения этого вычисления.
Вдоль верхнего пути мы встречаем орла, а затем снова орлы, или HH. Также умножаем:
50% * 50% =
(. 50) * (.50) =
.25 =
25%.
Это означает, что вероятность подбросить две головы составляет 25%.
Затем мы могли бы использовать диаграмму для ответьте на любой вопрос о вероятностях с участием двух монет. Например, какова вероятность того, что мы получим голову и хвост? Поскольку нам не был дан приказ, возможны варианты HT или TH с общей вероятностью 25% + 25% = 50%.