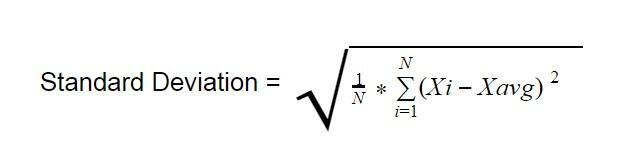Определение стандартного отклонения
Стандартное отклонение измеряет величину вариации или дисперсии в наборе значений данных относительно его среднего значения (среднего). Это статистический инструмент, используемый для интерпретации надежности данных. Он представлен символом «σ».
Если отклонение меньше, точки данных близки к среднему значению, и данные считаются
надежный. Напротив, если отклонение велико, точки данных разбросаны дальше от среднего значения; такие данные считаются менее надежными. Стандартное отклонение используется при анализе общего риска и доходности портфеля.
Оглавление
- Определение стандартного отклонения
- Объяснение стандартного отклонения
- Уравнение стандартного отклонения
- Расчет
- Пример
- Интерпретация
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Стандартное отклонение — это статистический инструмент, который измеряет волатильность данных. Он указывает, в какой степени значения выборки отклоняются от средних значений. Он вычисляется как квадратный корень из дисперсии и обозначается символом «σ» (греческая буква).
- σ не может быть отрицательным значением и может быть равен 0 только в том случае, если значения в наборе данных равны и не имеют вариаций.
- В финансах этот математический инструмент применяется для определения уровня рисков, связанных с конкретными инвестициями или активами. Метод измеряет спред соответствующих цен и доходов. Более высокое отклонение отражает высокую волатильность и наоборот.
- Если символ σ обозначает стандартное отклонение, n — общее количество наблюдений в наборе данных, xi — i-е количество наблюдений, а µ — выборочное среднее, то отклонение вычисляется по следующей формуле:
В большинстве случаев минимальное стандартное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.
Этот статистический инструмент помогает исследователям и аналитикам понять распространение данных, чтобы
определить степень разброса данных. Этот математический аппарат показывает
разброс выборочных значений от среднего значения.
Стандартные ошибки подчеркивают точность среднего значения выборки по отношению к генеральной совокупности.
означает, когда данные обширны и широко распространены. На графике отклонение может лежать влево, вправо или в обе стороны — формирование колоколообразной кривойГрафик колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее.
Уравнение стандартного отклонения
Уравнение для определения стандартного отклонения ряда данных выглядит следующим образом:
т.е. σ=√v
Также, µ =∑x/n
Здесь,
- σ — это символ, обозначающий стандартное отклонение.
- n — количество наблюдений в наборе данных.
- xi — i-е количество наблюдений в наборе данных.
- µ — среднее значение выборки.
- V — дисперсия.
- ∑x — сумма всех значений в наборе данных.
Расчет
Основные шаги, используемые для поиска и расчета стандартного отклонения, следующие:
- Сначала определите среднее значение набора данных.
- Затем подготовьте диаграмму со значениями выборки и разницей между выборкой.
значения и средние значения. - В следующем столбце найдите квадрат разностей.
- Чтобы получить дисперсию, сложите все квадраты и разделите результат на разницу между общим количеством наблюдений и 1.
- Наконец, найдите квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Пример
Давайте рассмотрим несколько примеров, чтобы понять практические последствия:
Найти отклонение цен на сырую нефть за год, когда среднемесячные цены за литр были следующими:
МесяцСредняя цена за литр в долларахЯнварь0,83Февраль0,81Март0,78Апрель0,82Май0,79Июнь0,75Июль0,76Август0,79Сентябрь0,81Октябрь0,77Ноябрь0,76Декабрь0,75
Решение:
Расчет среднего:
µ = ∑x/n
µ = 9,42/12
= 0,785 доллара за литр
С. №МесяцСредняя цена за литр в $ (x)х – 0,785 доллара США(х – 0,785 долл. США)21January0.830.0450.0020252February0.810.0250.0006253March0.78-0.0050.0000254April0.820.0350.0012255May0.790.0050.0000256June0.75-0.0350.0012257July0.76-0.0250.0006258August0.790.0050.0000259September0.810.0250.00062510October0.77-0.0150.00022511November0. 76-0.0250.00062512декабрь0.75-0.0350.00122512–9.42 0,0085
Расчет стандартного отклонения :
- σ = √ [0.0085 / (12-1)]
- σ = √ (0,00077272727)
- σ = 0,0277979724571285 долл. США
Таким образом, стандартное отклонение цен на нефть за литр для данного года равно
0,0277979724571285.
Интерпретация
Стандартное отклонение указывает на волатильность или дисперсию значений конкретного распределения. Он показывает, в какой степени значения выборки отклоняются от средних значений. Таким образом, эта мера облегчает сравнение и анализ.
Ниже приведены различные интерпретации полученного результата:
- Если σ велико, то волатильность анализируемых данных также высока.
- Точно так же, когда σ низкое, дисперсия между точками данных также незначительна.
- В распределении σ может быть равно 0 только тогда, когда разница между точками данных равна нулю. Это также наименьшее значение отклонения, которое можно получить.
- Невозможно получить отрицательное значение σ, так как числитель включает квадрат разности между выборочными значениями и средними значениями.
- Кроме того, количество наблюдений всегда больше 1; следовательно, знаменатель должен быть положительным значением.
- Стандартное отклонение измеряется в тех же единицах, что и значения распределения. Например, в приведенном выше примере σ выражается в долларах.
- Выбросы (чрезвычайно высокие или низкие значения) существенно влияют на измерения отклонения.
Часто задаваемые вопросы (FAQ)
Что такое стандартное отклонение?
Стандартное отклонение — это статистический метод, используемый для нахождения разброса данных в распределении с использованием средних значений. Обозначается символом «σ».
Как рассчитать стандартное отклонение?
Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Дисперсия — это сумма квадрата разности между каждым значением в наборе данных и их средними значениями, деленная на значение, полученное путем вычитания единицы из общего числа наблюдений.
Почему стандартное отклонение важно?
Он определяет степень изменчивости значений в выборочном распределении. Это широко используемый статистический инструмент в финансах, инвестициях и бизнесе для интерпретации величины риска, связанного с ценной бумагой или активом. В большинстве случаев минимальное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.
Может ли стандартное отклонение быть равным нулю?
Единственный случай, когда он может быть равен нулю, — это когда все точки данных в распределении одинаковы. Нулевое отклонение указывает на нулевой разброс или изменчивость значений. Для реальных сценариев это практически невозможно.
Рекомендуемые статьи
Эта статья была руководством к тому, что такое стандартное отклонение в статистике и его определение. Мы объясняем его уравнение, расчеты, символы, статистику и его интерпретацию. Подробнее об этом вы можете узнать из следующих статей —
- Стандартное отклонение в ExcelСтандартное отклонение в ExcelСтандартное отклонение показывает отклонение значений данных от среднего (среднего). В Excel СТАНДОТКЛОН и СТАНДОТКЛОН.С вычисляют стандартное отклонение выборки, а СТАНДОТКЛОН и СТАНДОТКЛОН.П вычисляют стандартное отклонение совокупности. СТАНДОТКЛОН доступен в Excel 2007 и предыдущих версиях. Однако СТАНДОТКЛОН.П и СТАНДОТКЛОН.С доступны только в Excel 2010 и последующих версиях. читать далее
- Примеры стандартных отклоненийПримеры стандартных отклоненийПримеры стандартных отклонений помогут вам применить формулу стандартного отклонения для определения риска, связанного с волатильностью финансовых ценных бумаг.Подробнее
- Формула стандартного отклоненияФормула стандартного отклоненияСтандартное отклонение (SD) — популярный статистический инструмент, обозначаемый греческой буквой «σ», для измерения вариации или дисперсии набора значений данных относительно их среднего (среднего) значения, таким образом интерпретируя надежность данных.Подробнее
-
1
Look at your data set. This is a crucial step in any type of statistical calculation, even if it is a simple figure like the mean or median.[2]
- Know how many numbers are in your sample.
- Do the numbers vary across a large range? Or are the differences between the numbers small, such as just a few decimal places?
- Know what type of data you are looking at. What do your numbers in your sample represent? this could be something like test scores, heart rate readings, height, weight etc.
- For example, a set of test scores is 10, 8, 10, 8, 8, and 4.
-
2
Gather all of your data. You will need every number in your sample to calculate the mean.[3]
- The mean is the average of all your data points.
- This is calculated by adding all of the numbers in your sample, then dividing this figure by the how many numbers there are in your sample (n).
- In the sample of test scores (10, 8, 10, 8, 8, 4) there are 6 numbers in the sample. Therefore n = 6.
Advertisement
-
3
Add the numbers in your sample together. This is the first part of calculating a mathematical average or mean.[4]
- For example, use the data set of quiz scores: 10, 8, 10, 8, 8, and 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. This is the sum of all the numbers in the data set or sample.
- Add the numbers a second time to check your answer.
-
4
Divide the sum by how many numbers there are in your sample (n). This will provide the average or mean of the data.[5]
- In the sample of test scores (10, 8, 10, 8, 8, and 4) there are six numbers, so n = 6.
- The sum of the test scores in the example was 48. So you would divide 48 by n to figure out the mean.
- 48 / 6 = 8
- The mean test score in the sample is 8.
Advertisement
-
1
Find the variance. The variance is a figure that represents how far the data in your sample is clustered around the mean.[6]
- This figure will give you an idea of how far your data is spread out.
- Samples with low variance have data that is clustered closely about the mean.
- Samples with high variance have data that is clustered far from the mean.
- Variance is often used to compare the distribution of two data sets.
-
2
Subtract the mean from each of your numbers in your sample. This will give you a figure of how much each data point differs from the mean.[7]
- For example, in our sample of test scores (10, 8, 10, 8, 8, and 4) the mean or mathematical average was 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 8 = 2, 8 — 8 = 0, 8 — 8 = 0, and 4 — 8 = -4.
- Do this procedure again to check each answer. It is very important you have each of these figures correct as you will need them for the next step.
-
3
Square all of the numbers from each of the subtractions you just did. You will need each of these figures to find out the variance in your sample.[8]
- Remember, in our sample we subtracted the mean (8) from each of the numbers in the sample (10, 8, 10, 8, 8, and 4) and came up with the following: 2, 0, 2, 0, 0 and -4.
- To do the next calculation in figuring out variance you would perform the following: 22, 02, 22, 02, 02, and (-4)2 = 4, 0, 4, 0, 0, and 16.
- Check your answers before proceeding to the next step.
-
4
Add the squared numbers together. This figure is called the sum of squares.[9]
- In our example of test scores, the squares were as follows: 4, 0, 4, 0, 0, and 16.
- Remember, in the example of test scores we started by subtracting the mean from each of the scores and squaring these figures: (10-8)^2 + (8-8)^2 + (10-8)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- The sum of squares is 24.
-
5
Divide the sum of squares by (n-1). Remember, n is how many numbers are in your sample. Doing this step will provide the variance. The reason to use n-1 is to have sample variance and population variance unbiased. [10]
- In our sample of test scores (10, 8, 10, 8, 8, and 4) there are 6 numbers. Therefore, n = 6.
- n-1 = 5.
- Remember the sum of squares for this sample was 24.
- 24 / 5 = 4.8
- The variance in this sample is thus 4.8.
Advertisement
-
1
Find your variance figure. You will need this to find the standard deviation for your sample.[11]
- Remember, variance is how spread out your data is from the mean or mathematical average.
- Standard deviation is a similar figure, which represents how spread out your data is in your sample.
- In our example sample of test scores, the variance was 4.8.
-
2
Take the square root of the variance. This figure is the standard deviation.[12]
- Usually, at least 68% of all the samples will fall inside one standard deviation from the mean.
- Remember in our sample of test scores, the variance was 4.8.
- √4.8 = 2.19. The standard deviation in our sample of test scores is therefore 2.19.
- 5 out of 6 (83%) of our sample of test scores (10, 8, 10, 8, 8, and 4) is within one standard deviation (2.19) from the mean (8).
-
3
Go through finding the mean, variance and standard deviation again. This will allow you to check your answer.[13]
- It is important that you write down all steps to your problem when you are doing calculations by hand or with a calculator.
- If you come up with a different figure the second time around, check your work.
- If you cannot find where you made a mistake, start over a third time to compare your work.
Advertisement
Practice Problems and Answers
Add New Question
-
Question
What is the standard deviation of 10 samples with a mean of 29.05?
Depends on the 10 samples of data. If all ten numbers were 29.05 then the standard deviation would be zero. Standard deviation is a measure of how much the data deviates from the mean.
-
Question
How do I calculate the standard deviation of 5 samples with the mean of 26?
You take the average of 26 and 5, divide by b squared and multiply by deviation equation constant.
-
Question
How do I find the standard deviation of 10 samples with a mean of 29.05?
Take each sample and subract the mean. Next, square each result, getting rid of the negative. Add the 10 results and divide the sun by 10 — 1 or 9. That is the standard deviation.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate standard deviation, start by calculating the mean, or average, of your data set. Then, subtract the mean from all of the numbers in your data set, and square each of the differences. Next, add all the squared numbers together, and divide the sum by n minus 1, where n equals how many numbers are in your data set. Finally, take the square root of that number to find the standard deviation. To learn how to find standard deviation with the help of example problems, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 2,559,851 times.
Reader Success Stories
-
«This article was the best statistics instructor I have ever been taught by. I have learned more from this little…» more
Did this article help you?
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
- среднеквадратическое отклонение,
- среднее квадратическое отклонение,
- среднеквадратичное отклонение,
- квадратичное отклонение,
- стандартный разброс.
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
- в финансах в качестве меры волатильности,
- в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.
Пример:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
- А -> (19 + 21 + 19+ 21) / 4 = 20
- Б -> (15 + 26 + 15+ 24) / 4 = 20
Однако, глядя на цифры, можно заметить:
- в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
- в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
- стандартное отклонение компании A = 1,
- стандартное отклонение компании Б ≈ 5.
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения

σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
- Вычесть среднее значение из каждого числа
- Возвести каждый результат в квадрат (так получатся квадраты разностей)
- Найти среднее значение квадратов разностей.
Ещё расчёт дисперсии можно сделать по этой формуле:

S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
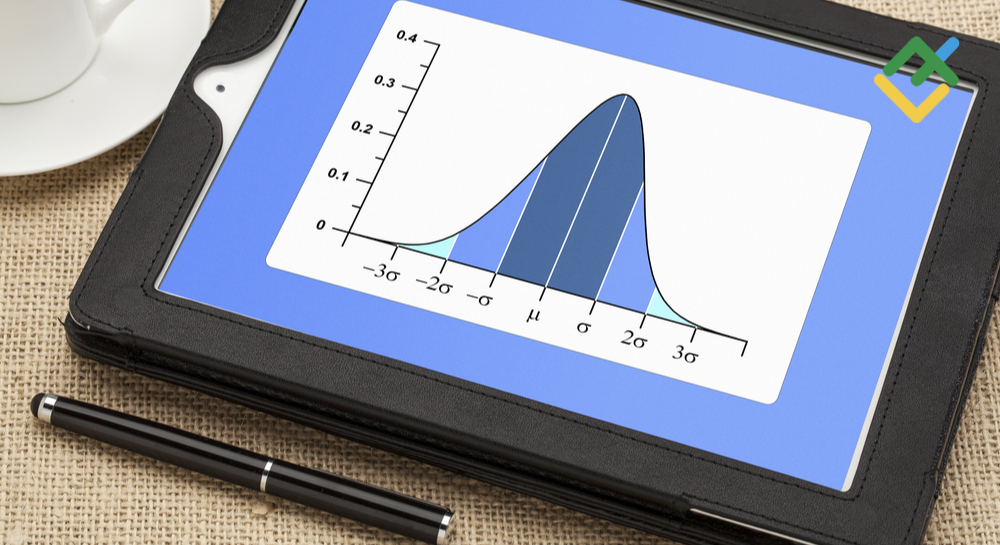
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
- при <10% выборка слабо вариабельна,
- при 10% – 20 % — средне вариабельна,
- при >20 % — выборка сильно вариабельна.
Узнайте также про:
- Корреляции,
- Метод Крамера,
- Метод наименьших квадратов,
- Теорию вероятностей
- Интегралы.
В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).
Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).
Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
| Порода собаки | Рост в миллиметрах |
| Ротвейлер | 600 |
| Бульдог | 470 |
| Такса | 170 |
| Пудель | 430 |
| Мопс | 300 |
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего:
Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм2.
Таким образом, дисперсия составляет 21704 мм2.
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм2.
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
.
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
.
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
.
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич
Как определить текущую волатильность и силу тренда? На каком расстоянии от усредненного значения цены и точки входа в рынок устанавливать стоп-лосс? Если ли в текущий момент на рынке флет? На все эти вопросы помогает ответить индикатор Standard Deviation. О том, как он работает и как его применять на практике в трендовых стратегиях с другими индикаторами, вы узнаете в этом обзоре.
В этой статье мы разберем:
- Что такое индикатор Standard Deviation
- Как рассчитать индикатор Standard Deviation
- Как использовать индикатор Standard Deviation в торговле?
- Как настроить индикатор Standard Deviation
- Торговые стратегии с индикатором Standard Deviation
- FAQ по индикатору Standard Deviation
Понятие стандартного отклонения пришло в трейдинг из математического анализа, точнее — из описательной статистики. Оно показывает величину среднего отклонения данных относительно их среднего значения за выбранный период. В статистике обозначается греческой буквой «σ» — «сигма».
Перед тем, как перейти к индикатору Standard Deviation, напомню о том, зачем трейдеру нужно учитывать волатильность и что такое SMA.
Волатильность.
Волатильность — это диапазон изменяемости цены за фиксированный промежуток времени. В трейдинге ее можно применять следующим образом:
- Для поиска тренда. Нет волатильности — нет торговли. Если цена практически не отходит от своего среднего значения, то есть почти не меняется, сделку открыть возможности нет. Рост волатильности означает появление сильного текущего движения цены.
- Для поиска окончания тренда и возможного разворота. Если значение волатильности достигает своего максимума, намечается окончание тренда. Экстремумы сравниваются визуально с аналогичными экстремумами на ранних периодах.
- Для постановки стопов. Если на рынке наблюдается волатильность в обе стороны, на каком расстоянии от открытой сделки ставить стоп-лосс так, чтобы ценовая линия его не зацепила? В соответствии со средней волатильностью на более высоких таймфреймах. По такому же принципу можно устанавливать и тейк-профит.
Оценивать волатильность можно по-разному. Например, для дневного интервала волатильность за 1 день — это расстояние в пунктах между ценами High и Low. Эти значения можно найти в калькуляторе. Пример такого калькулятора на сайте Investing.
Также можно оценивать волатильность визуально относительно средней скользящей — чем дальше от нее цена, тем больше волатильность.
Еще один метод — оценка изменения текущей цены в процентах относительно цены закрытия предыдущего периода. Если котировки изменились в пределах 3%, волатильность небольшая, если на 10% — большая. Цифры условны и для каждой валютной пары свои.
Простая средняя скользящая
SMA — это индикатор технического анализа, который рассчитывается как среднее арифметическое цен выборки. Его недостаток в том, что он не учитывает волатильность цен внутри выбранного диапазона. В качестве примера возьму две числовые последовательности:
- 8, 7, 12, 2, 6.
- -30, 66, 7, 12, -20.
Можно ли сказать, что они одинаковы при том, что значение SMA в обеих ситуациях будет равно 7? Несмотря на одинаковое среднее значение выборки, разброс цен отличается. И называется этот разброс волатильностью.
Что такое Standard Deviation
В трейдинге среднее арифметическое — это простая средняя скользящая. Относительно нее цена может отклоняться на то или иное количество пунктов. Чем больше текущее отклонение цены от своего среднего значения, тем больше волатильность. Измеряет степень волатильности Standard Deviation (StdDev) — индикатор стандартного отклонения.
Standard Deviation считается трендовым индикатором — по нему можно находить моменты усиления тренда. Чем больше волатильность, тем сильнее тренд. Но так как он показывает статистическое отклонение цены от ее среднего значения в обе стороны, инструмент также используют и в канальных индикаторах. Если значение индикатора относительно невелико, рынок спокоен и нужно ожидать ценовой всплеск. И наоборот, если значение индикатора слишком велико, приближается к экстремальному, активность трейдеров скоро пойдет на убыль.
Особенности индикатора Standard Deviation:
- Эффективен на инструментах с большой и средней волатильностью.
- Применяется в трендовых стратегиях для поиска момента выхода цены из флета и начала тренда. Не подходит для скальпинга из-за запаздывания.
- Больше подходит для валютных пар, чем для фондовых и товарно-сырьевых активов. Валютный рынок характеризуется частой сменой тренда и глубокими коррекциями, на которых можно искать точки открытия сделок. Фондовый рынок более стабильный.
- Оптимальный таймфрейм — от М30. На коротких периодах М1-М5 есть ценовой шум — хаотичное движение цены в разные стороны, нарушающее логику построения индикатора.
- Часто двигается горизонтально в нижних точках, редко показывает горизонтальное плато на экстремумах. Чаще всего после начала роста движение волнообразное.
Одна из рабочих тактик — поиск роста волатильности на более длинном таймфрейме и использование этого движения на 1-2 стандартных таймфрейма ниже.
Плюсы индикатора Standard Deviation:
- Простая интерпретация. Чем больше значение индикатора, тем выше волатильность.
Минусы индикатора Standard Deviation:
- Запаздывание. Ценовая линия уже вышла из флета, а индикатор еще показывает низкую волатильность.
- Не показывает направление тренда. Если линия стандартного отклонения начинает расти, то это говорит о том, что цена все больше отклоняется от среднего значения. Но отклоняться она может как вверх, так и вниз.
Нельзя открывать сделки, опираясь только на уровень рыночной волатильности, потому для самостоятельных торговых систем Standard Deviation используется редко. Его можно сочетать с трендовыми индикаторами в качестве подтверждающего сигнал инструмента. Ниже я рассмотрю несколько интересных стратегий, построенных на комбинации Standard Deviation с еще одним индикатором волатильности ATR и уровнями Фибоначчи.
Как рассчитать индикатор Standard Deviation
Standard Deviation — это среднеквадратичное отклонение, математический термин, определяющий параметр рассеивания значений случайной величины. Формула расчета:
,где
- N — количество значений цен в выборке, определяется в настройках индикатора.
- Хi— i-тый член выборки. По умолчанию цена закрытия каждой свечи выбранного анализируемого интервала.
- Xavg— среднее арифметическое значений цен выборки. Или, говоря языком технического анализа, простая средняя скользящая (SMA).
Пошаговый расчет значения индикатора выглядит следующим образом:
- Рассчитывается среднее арифметическое значений за выбранный интервал. Например, если в настройках указан период 20, то рассчитывается среднее арифметическое цены за последние 20 свечей. По умолчанию используются цены закрытия.
- Полученное значение вычитается из каждого значения цены расчетного периода.
- Все числа возводятся в квадрат и суммируются.
- Полученная сумма делится на количество значений в выборке. То есть на число периода, указанное в настройках.
- Из результата извлекается квадратный корень. Это и есть стандартное отклонение.
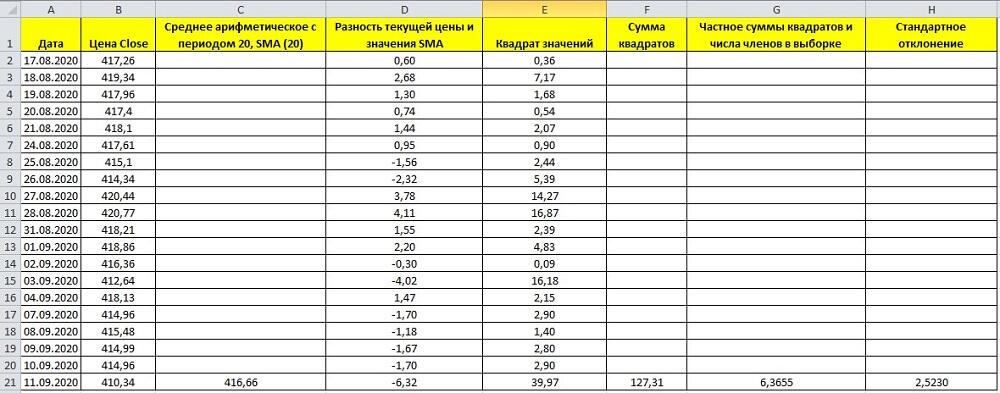
Практический пример расчета стандартного отклонения в Excel:
Этапы вычисления:
1. Вносим значения цен в колонку В. Эти данные можно выгрузить из МТ4 или взять у брокера. Количество строк соответствует периоду индикатора. Так как по умолчанию установлен период 20, в таблице 20 строк.
2. В ячейку С21 вносим формулу
=СРЗНАЧ(B2:B21)
Это среднее арифметическое, имеющее в техническом анализе название «Простая средняя скользящая».
3. Рассчитываем разность каждого значения цены и среднего арифметического. В ячейке D1 указываем:
=B2-$C$21
Растягиваем формулу на все ячейки.
4. Рассчитываем квадрат значений. В ячейку Е2 вносим формулу:
=D2^2
Растягиваем формулу на все ячейки.
5. В ячейке F21 суммируем все значения предыдущей колонки, в ячейке G21 делим результат на 20.
6. В ячейке Н21 рассчитываем стандартное отклонение:
=G21^(1/2)
Ссылку на шаблон таблицы вы найдете здесь. Также в интернете можно найти калькуляторы расчета стандартного отклонения. Но в них неудобно копировать котировки, которые сразу выгружаются в Excel.
Как использовать индикатор Standard Deviation в торговле?
Standard Deviation используется в трендовой торговле. Если индикатор находится на максимуме или растет большую часть времени, открывать сделку уже поздно, ждем флет или разворот тренда. Сигнал на открытие сделки — рост значения линии индикатора со своих минимумов.
1. Стратегия торговли по выходу из флета.
Консервативная стратегия. Во время флета отклонение цены от своего среднего значения минимально, индикатор находится внизу. Сигнал на открытие сделки — StdDev начинает расти, выходит за пределы своего флетового коридора. Как только свеча пробивает диапазон флета, на следующей свече открываем сделку в направлении тренда. Сделка закрывается в момент начала разворота индикатора.
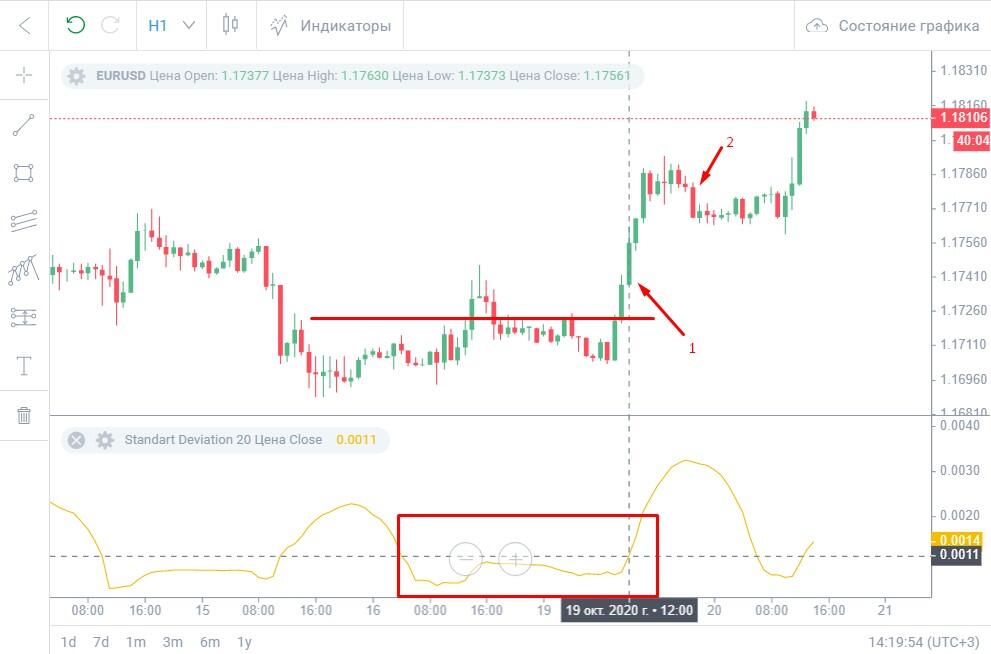
Пример.
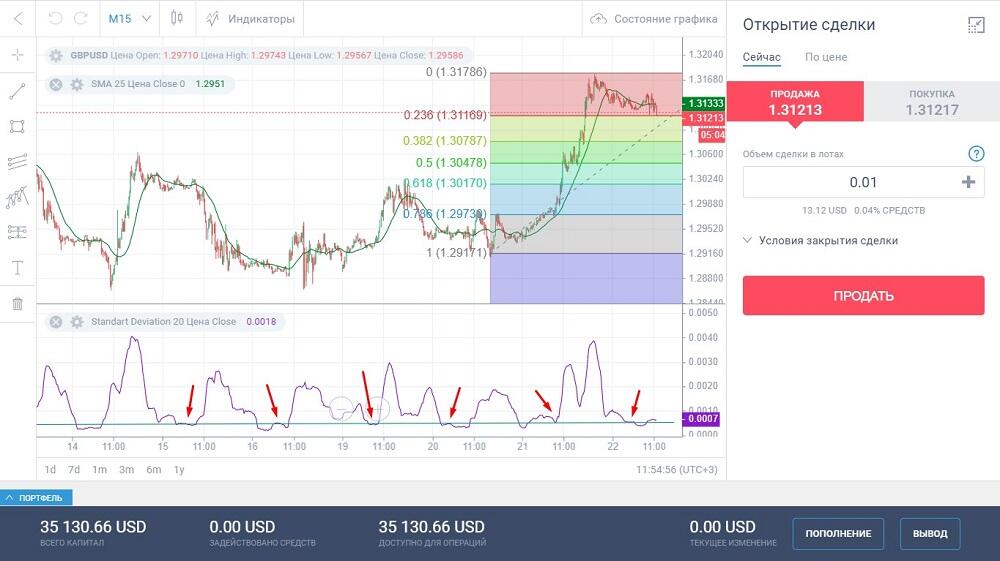
На предпоследней волне StdDev наблюдался нисходящий тренд, перешедший в горизонтальное движение. Максимальное значение индикатора в горизонтальном движении — 0,0009. В точке «1» видим, что ценовая линия пробила уровень сопротивления и зеленая свеча закрылась почти на уровне предыдущего локального пика. В этот же момент StdDev начинает расти — его значение 0,0011. Открываем сделку.
В точке «2» на красной свече, которая может предопределять разворот, StdDev также начинает разворачиваться. Закрываем сделку. Прибыль составила бы не менее 300 пунктов по 5-тизначным котировкам.
2. Стратегия обнаружения раннего разворота тренда.
Агрессивная стратегия. Предусматривает раннее открытие сделок по волнам Standard Deviation. Ее преимущество в том, что она позволяет решить проблему запаздывания индикатора. Сигналы частые, так как не нужно ждать зону флета, но процент ложных выше, чем в предыдущей стратегии.
Условия открытия сделки:
- Рисуем уровень поддержки для StdDev по его минимумам. Для интервала Н1 берем участок длиной 2-3 недели.
- Сделка открывается в момент пересечения индикатором уровня поддержки и дальнейшего роста.
- Направление сделки определяется так. Если предыдущая половина волны соответствовала нисходящему тренду, открываем длинную позицию. Если на предыдущей половине волны был восходящий тренд — короткую позицию.
Если предыдущей половине волны предшествовал флет, руководствуемся предыдущей стратегией. Если волна имела 2 и более вершин, делим ее пополам. Если волна не ярко выражена, несимметрична или нельзя идентифицировать ее начало и конец, сигнал игнорируется.
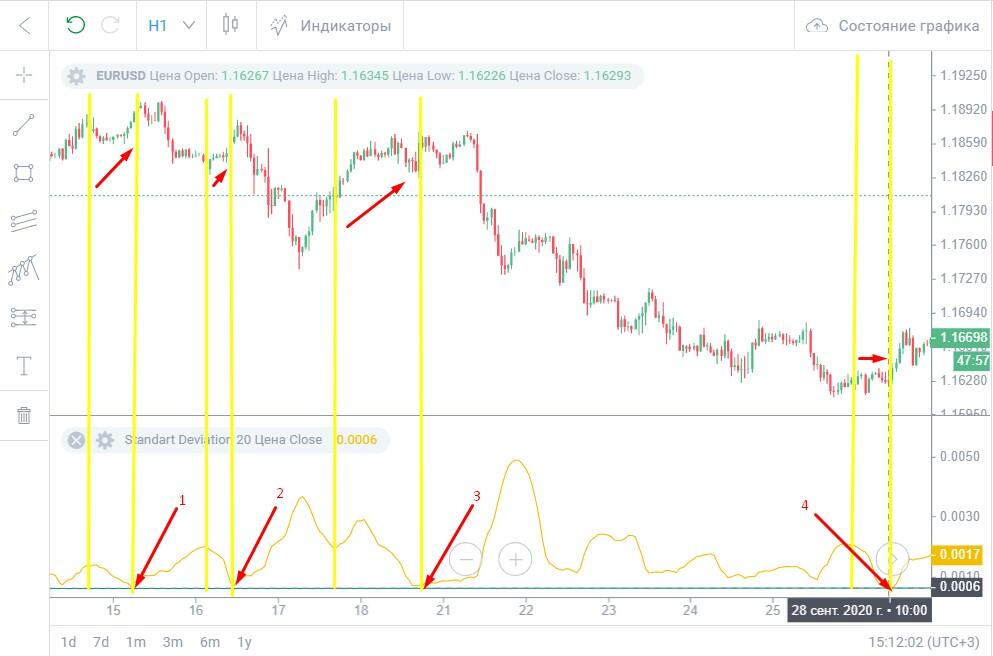
Пример.
Индикатор касается уровня в четырех точках. В половину волны перед точкой «1» тренд имел восходящее движение, потому в этой точке открываем короткую позицию. В точке «2» ситуация аналогичная. В точке «3» волна с двумя вершинами, потому половину отсчитываем от впадины. Тренд восходящий, потому в этой точке открываем короткую позицию. В точке «4» флет. Не торопимся открывать сделку до тех пор, пока свечи не покажут направление тренда.
В этих ситуациях сигнал лучше игнорировать или искать подтверждение. В первом случае волну нельзя точно идентифицировать, во втором случае волна несимметрична.
Высокое стандартное отклонение
Есть числовая последовательность цен закрытия последних 5 свечей: 4, 5, 3, 4, 6. Рассеивание относительно небольшое. Среднее арифметическое — 4,4. Минимальной и максимальной ценой будут цены 3 и 6, что в процентах составляет соответственно 31,8% и 36,4%. Допустим, что для данного инструмента такие отклонения за фиксированный период времени — стандартная ситуация, соответствующая флету.
Цена постепенно начинает расти. Числовая последовательность через три свечи уже несколько иная: 4, 6, 10, 14, 13. Средняя цена теперь 9,4. Минимальное и максимальное значения — 4 и 14, что в процентах составляет 57,45% и 48,93%. Если в первом случае цена отклонялась от своего среднего значения в среднем на треть, то теперь цена отклоняется от среднего значения в среднем на 50%.
Волатильность растет. Теперь посмотрим, как ведет себя стандартное отклонение. Для первой ситуации оно составит:
Для второй ситуации:
Вместе с ростом цены и волатильности более чем в три раза увеличилось и стандартное отклонение. Высокое стандартное отклонение означает, что цена изменяется в ту или иную сторону. Увеличение стандартного отклонения с каждой свечой означает, что на рынке наблюдается тренд и цена все дальше отклоняется вверх или вниз от своего среднего значения. По достижении Standard Deviation максимума возможны следующие ситуации:
- Цена уйдет во флет. Через три свечи ценовой ряд будет выглядеть, например, так: 14, 13, 15, 14, 12. Среднее значение вырастет, на графике SMA относительно первой ситуации поднимется выше. Но стандартное отклонение снова вернется к значению 0,5099. На графике индикатора будет видна волна с боковыми значениями 0,5099 и пиковым значением 1,9391.
- Цена развернется. Через три свечи ценовой ряд будет выглядеть, например, так: 14, 13, 8, 5, 7. Значение SMA будет равно 9,4, значение индикатора Standard Deviation — 1,7493. То есть останется почти на том же уровне, несмотря на смену направления тренда.
На графике это выглядит так:
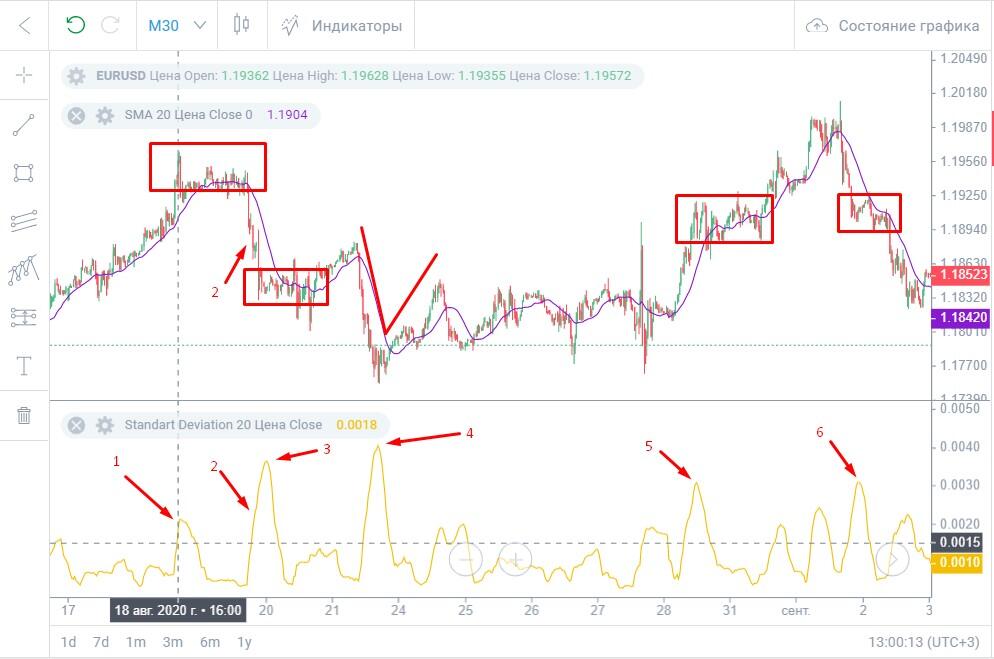
Вопрос в том, что называть «высоким стандартным отклонением». Чтобы понять, как долго на рынке будет сохраняться тренд, нужно сравнить текущее значение Standard Deviation с другими визуальными экстремумами.
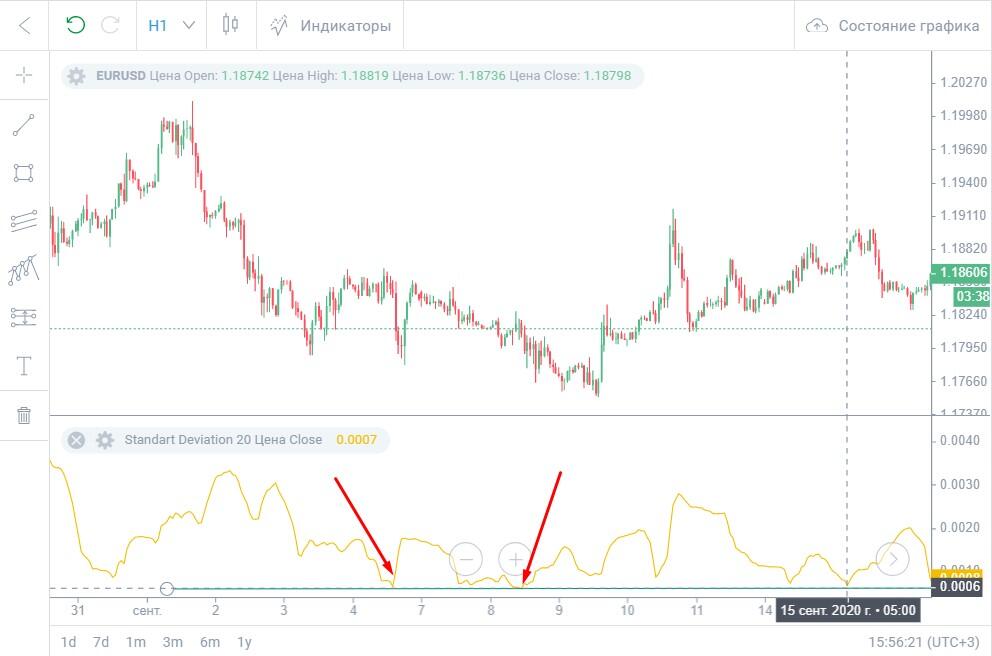
Пунктирная линия на скрине находится на визуальном среднем уровне Standard Deviation. Большую часть времени индикатор или находился ниже этого уровня, или пересекал его на короткое время. Потому значения, которые находятся значительно выше этого уровня, можно считать высокими.
- В точке «1» локальный экстремум. В момент разворота линии индикатора на графике начинается флет. Флетовые зоны выделены на скрине красными прямоугольниками.
- В точке «2», находящейся на том же уровне, что и точка «1», StdDev продолжает восходящее движение. Значит, тренд все еще продолжается, но скоро может закончиться. В точке «3» с разворотом линии индикатора начинается флет.
- В точке «4» на пиковом значении StdDev происходит разворот тренда. Разворотное восходящее движение не настолько сильное, как предыдущее нисходящее, потому индикатор уходит вниз.
- В точках «5» и «6» в момент разворота индикатора наступает флет.
Вывод. Высокое значение стандартного отклонения может означать, что восходящий или нисходящий тренд еще продолжается, но входить в рынок уже поздно. Максимальное значение стандартного отклонения и последующий разворот означают смену направления тренда или переход во флет.
Низкое стандартное отклонение
Низкое стандартное отклонение означает, что цена практически не отходит от своего среднего значения, рассчитанного за фиксированный период времени. Это может означать следующее:
1. На рынке флет. Объемы заявок «быков» и «медведей» сравнительно одинаковы или объемы торгов незначительны. Цена практически не отходит от своего среднего значения.
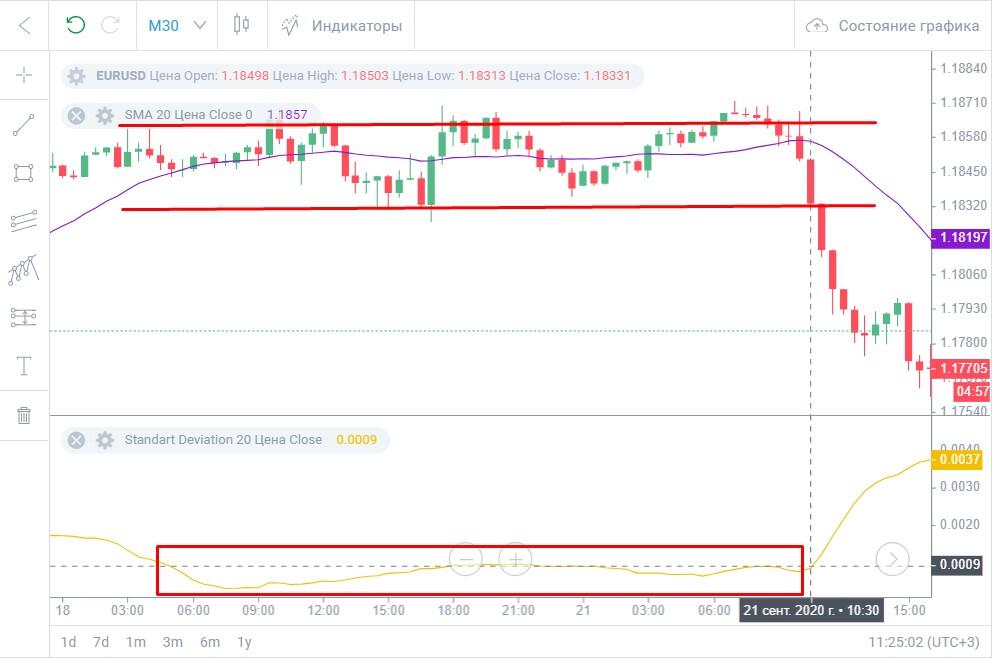
Пример:
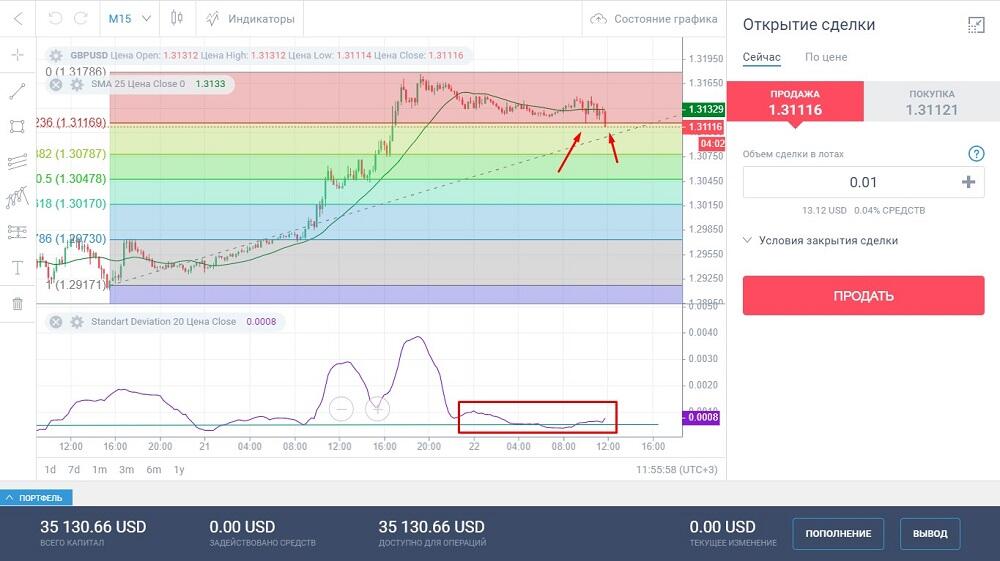
На график добавлена SMA с таким же периодом 20, как и у StdDev. Линия индикатора движется почти в самом низу рядом с уровнем 0,0009. Низкое стандартное отклонение соответствует флету — движению цены в относительно узком коридоре. Как только цена пробивает нижний уровень диапазона, начинается рост значения стандартного отклонения, и одновременно цена начинает быстро удаляться от SMA.
2. Движение цены плавное. Цена изменяется постепенно с небольшим отклонением от своего предыдущего значения.
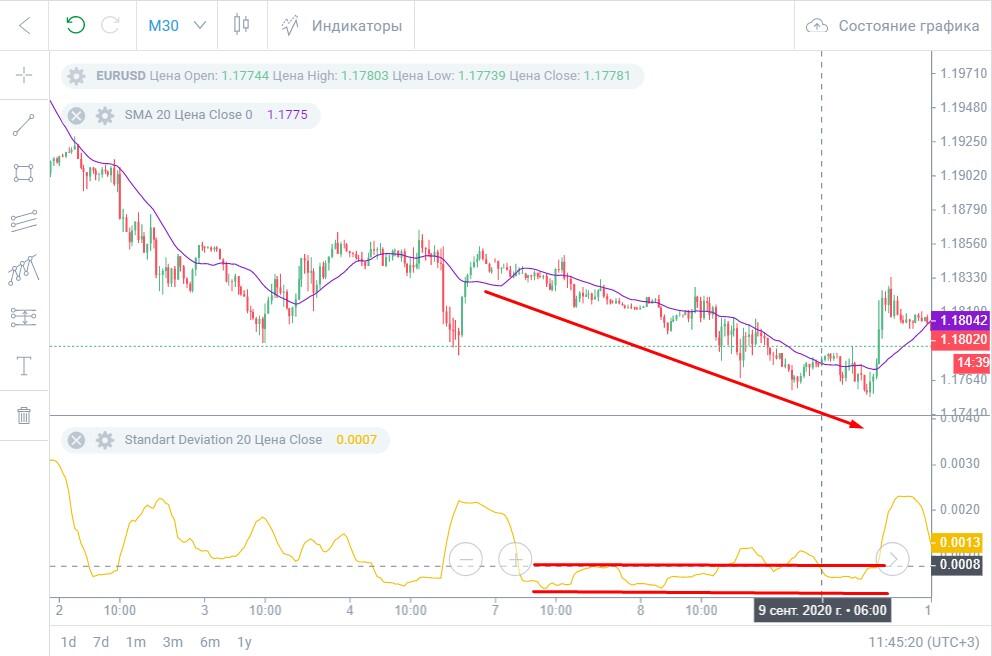
Пример:
Относительно пиковых значений и волн на выделенном участке значение StdDev можно назвать небольшим. Тем не менее, на этом участке наблюдается плавный нисходящий тренд.
Вывод. Низкое стандартное отклонение может говорить как о наличии флета, так и о наличии медленно растущего/падающего тренда.
Важно! Фиксированный период, он же период в настройках Standard Deviation, имеет ключевое значение. Например, для периода 3 стандартное отклонение в числовом ряду 5, 6, 30 будет относительно низким — 4,4759, а для периода 10 в числовом ряду 4, 3, 6, 5, 7, 5, 6, 5, 6, 30 относительно высоким — 5,3108. Чем длиннее стабильный ценовой ряд выборки и чем резче изменится цена на последней свече, тем больше будет стандартное отклонение.
Как настроить индикатор Standard Deviation
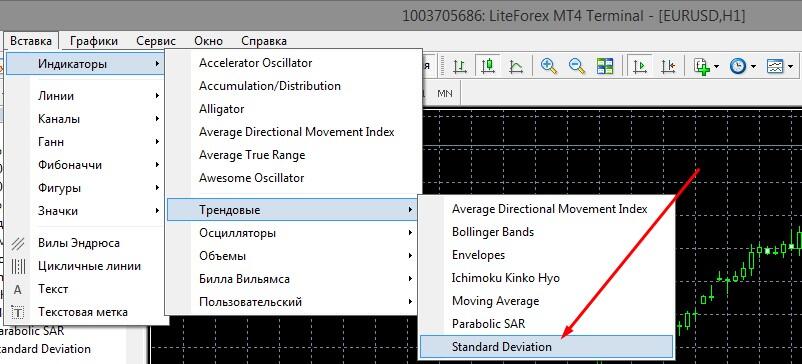
Индикатор входит в число базовых многих торговых платформ. В терминале LiteFinance его можно установить так:
1. Откройте терминал: на сайте LiteFinance в верхнем меню выберите вкладку «Начинающим/Открыть демо-счет». Регистрация не нужна — вы сразу же переходите во встроенную торговую платформу.
2. Выберите торговый инструмент: нажмите в левой панели опцию «Торговать», откройте график нужной валютной пары.
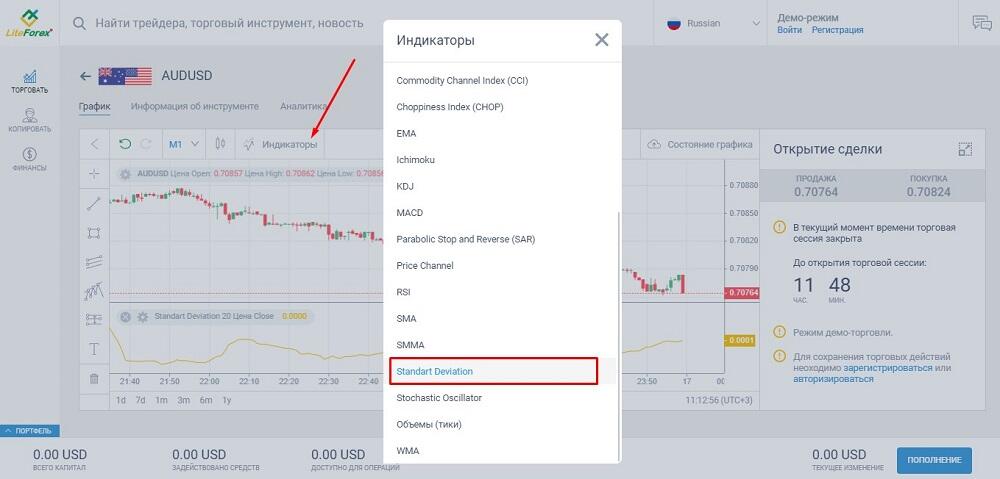
3. В списке индикаторов выберите Standard Deviation.
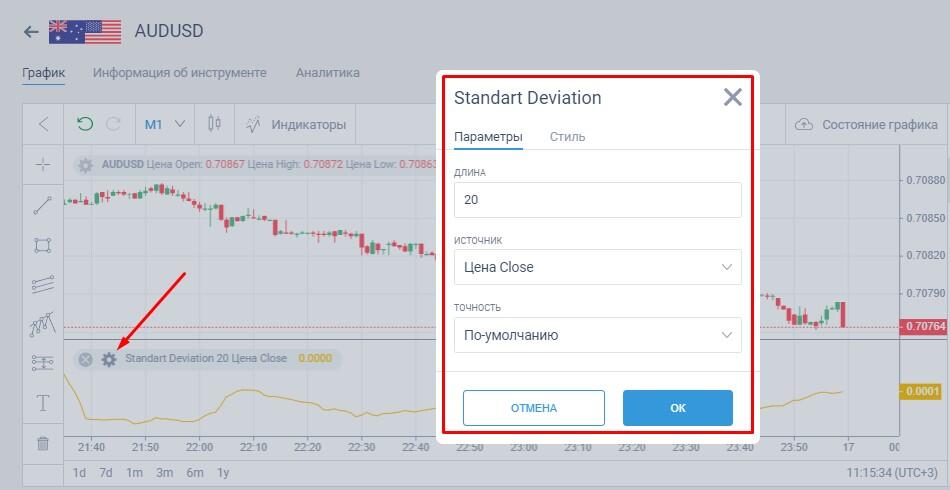
Индикатор появится под графиком цены. Для вызова настроек нажмите шестеренку.
Стандартные настройки:
1. Длина — период индикатора. Количество свечей, которые будут учитываться в расчете. По умолчанию выборка составляет 20 последних свечей.
- Чем больше период, тем быстрее и резче реагирует индикатор на изменение цены.
- Чем меньше период, тем менее резко движение индикатора.
Это одно из кардинальных отличий StdDev от других индикаторов. Например, если взять SMA, то увеличение периода наоборот ведет к замедлению индикатора — чем длиннее выборка, тем меньший вес последней цены в ценовой последовательности. У StdDev наоборот.
2. Источник — цена, которая принимает участие в расчете:
- Close — цена закрытия свечи.
- Open — цена открытия свечи.
- High — максимальное значение цены в выбранном таймфрейме, верхняя крайняя точка тени.
- Low — минимальное значение цены в выбранном таймфрейме, нижняя крайняя точка тени.
- Медиана — цена = (High + Low)/2.
- Медиана HLC — цена = (High + Low + Close)/3.
- Медиана HLOC — цена = (High + Low + Open + Close)/4.
3. Точность — количество знаков после запятой в значении индикатора, которое отображается на шкале справа.
Во вкладке «Стиль» можно выбрать цвет, толщину линии индикатора или изменить ее сплошное отображение на пунктир.
Индикатор размещается под графиком цены и представляет собой одну линию, движущуюся выше отметки «0» вверх или вниз в неограниченном диапазоне. Чем больше значение индикатора, тем выше рыночная волатильность.
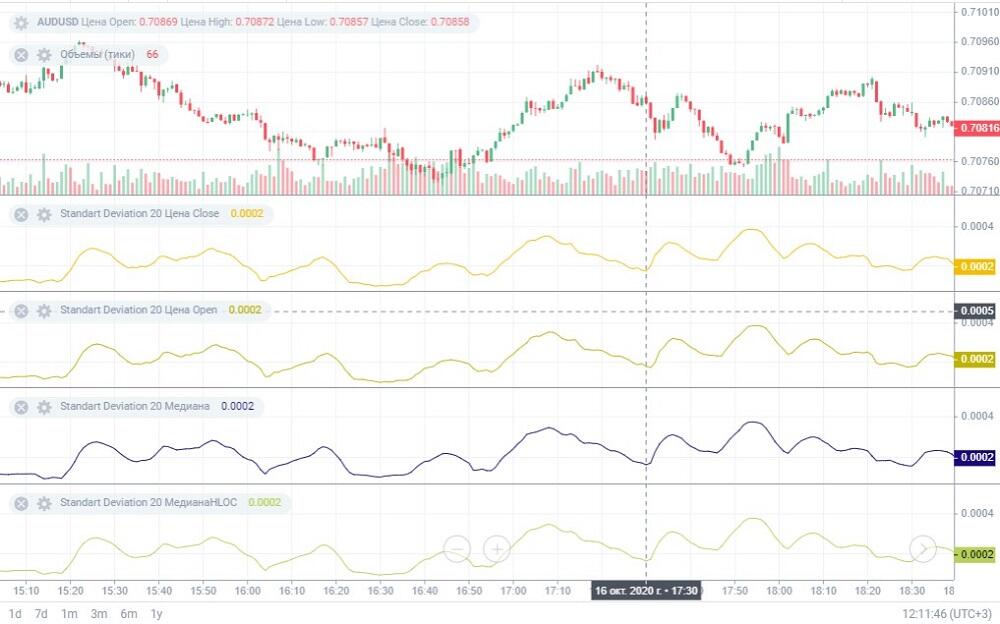
Тип цены можно оставить по умолчанию Close. Ниже график StdDev с несколькими разными типами цен. Отличий в построении линии почти нет кроме того, что индикатор, построенный по ценам Close, на 1-2 свечи опережает остальные.
Standard Deviation в MT4
Настройки StdDev в МТ4 немного отличаются от тех, которые есть в кабинете LiteFinance. Но и в МТ4 индикатор входит в число базовых. Найти его можно здесь: «Вставка/Индикаторы/Трендовые».
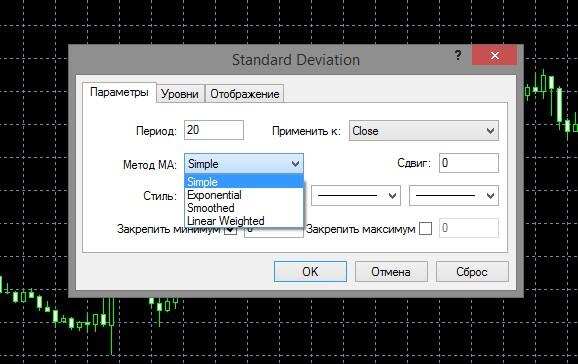
Настройки:
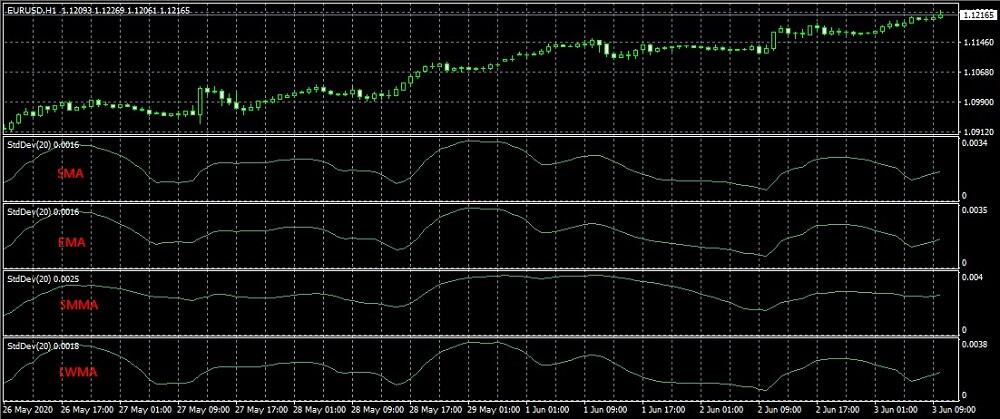
Основное отличие настроек в МТ4 — здесь можно переключить тип средней скользящей, используемой в формуле. Если в базовой версии рассчитывается среднее арифметическое (Simple), то в МТ4 можно выбрать экспоненциальную скользящую, SMMA и LWMA.
Отличия существенные — разница в сглаженности линии и размере амплитуды. Какой вариант лучше, какой хуже — ответа нет. Совет: подбирайте параметры под отдельные активы и отдельные рыночные ситуации.
Модификации и другие индикаторы, построенные на основе Standard Deviation:
- Juicenew — индикатор, в основе которого лежит инструмент StdDev. Он удобен с визуальной точки зрения. Вместо линии, которую можно трактовать по-разному, здесь гистограмма со столбиками двух разных цветов. Сигналы с точной интерпретацией без спорных моментов: «или есть сигнал, или нет». Скачать этот индикатор для МТ4 можно по этой ссылке.
- Полосы Боллинджера — стандартный канальный индикатор многих торговых платформ. Состоит из трех линий: центральная — обычная средняя скользящая, линии границ каналов — средние скользящие, смещенные на определенное число стандартных отклонений (StdDev).
Торговые стратегии с индикатором Standard Deviation
Как использовать StdDev, покажу на примере двух стратегий. Первая — это сочетание StdDev с еще одним определяющим уровень волатильности индикатором — ATR. Вторая — торговля по уровням Фибоначчи с использованием StdDev в качестве вспомогательного.
Standard Deviation и ATR
ATR используется для определения степени волатильности рынка. Подробнее о нем вы можете прочесть в обзоре «Индикатор ATR — волатильность под контролем трейдера».
Вводные данные:
- Валютная пара — GBP/USD.
- Таймфрейм — Н1.
- Настройки индикаторов: StdDev (20), ATR (20). Периоды обоих индикаторов должны совпадать.
Суть стратегии — открытие сделки в момент усиления тренда, которое подтверждается совпадением сигналов обоих индикаторов.
Условия открытия позиции:
- ATR пересекает свой уровень поддержки снизу вверх или отскакивает от него вверх и продолжает расти.
- StdDev пересекает свой уровень поддержки снизу вверх или отскакивает от него вверх и продолжает расти.
На следующей свече после совпадения обоих условий открываем сделку в направлении начавшегося тренда. Стоп-лосс ставим за локальным экстремумом.
Варианты выхода из рынка:
- В момент формирования разворотного паттерна. Например, пин-бара.
- В момент начала разворота одного из индикаторов.
Не открываем позицию, если:
- Один из индикаторов только оттолкнулся от уровня поддержки, второй уже прошел более 50% пути до уровня сопротивления.
- Предполагается выход новостей с максимальной отметкой важности по экономическому календарю.
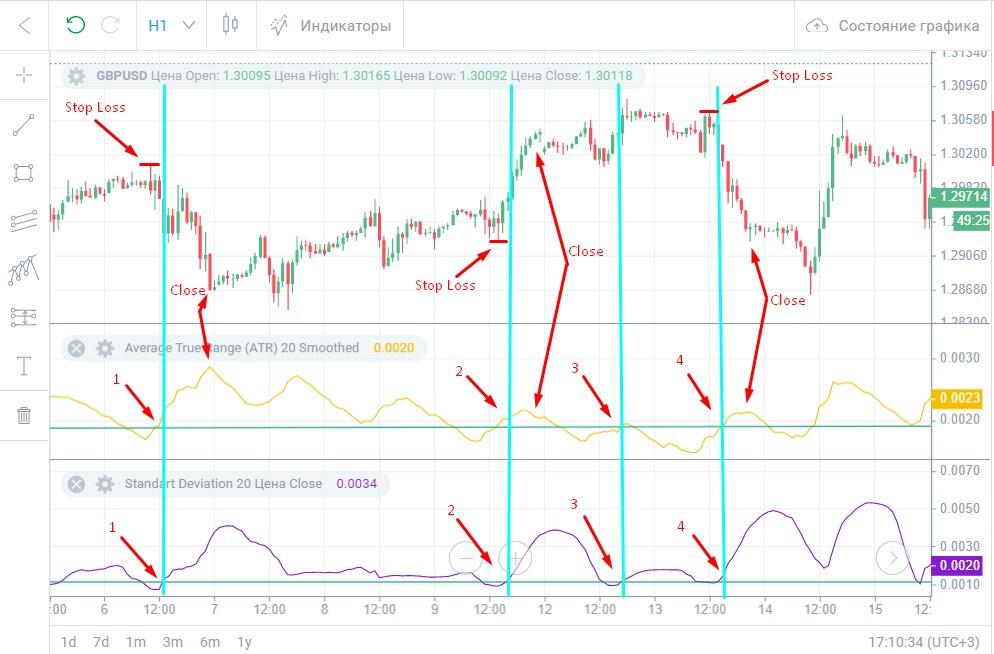
Пример.
Первый шаг — построение уровней поддержки для обоих индикаторов. Для этого нужно максимально уменьшить масштабирование графика и провести горизонтальную линию по тому уровню, на котором чаще всего разворачивались индикаторы. Затем вернуть удобное масштабирование и продлевать линии уровней по мере дальнейшего движения цены.
В точке «1» есть выполнение обоих условий. StdDev первым пробивает свой уровень поддержки и уходит вверх, ждем подтверждения от ATR. Как только оно получено, открываем короткую позицию. Направление подсказывают падающие свечи. Стоп — за ближайший локальный максимум с отступом от конца тени 2-3 пункта. Сделку закрываем в момент разворота ATR. Правильность решения подтверждает и сформированный зеленой свечой пин-бар.
В точке «2» также совпадение обоих условий, но вопрос с моментом закрытия сделки. Если ориентироваться на ATR, то сделка могла бы быть закрыта досрочно. Увы, единых рекомендаций по выходу из рынка нет, потому советую ориентироваться по ситуации. В точке «4» ситуация аналогичная.
Точка «3». При совпадении сигналов здесь имел бы смысл открывать длинную позицию, но оба индикатора тут же разворачиваются. Сигнал ложный, сделку лучше закрыть вручную, не дожидаясь срабатывания стопа.
Standard Deviation и уровни коррекции Фибоначчи — практический пример
Стратегия называется «Скальпинг по уровням коррекции Фибоначчи и StdDev». Суть скальпинга по уровням коррекции заключается в том, чтобы поймать основной тренд, дождаться локального отката до уровней Фибоначчи и открыть сделку в сторону тренда с тейк-профитом на следующем уровне. О том, как работать с уровнями коррекции Фибоначчи и их производными инструментами, вы можете прочесть в обзоре «Что такое уровни Фибоначчи».
Проблема определения точки входа заключается в нескольких моментах:
- Сигналом считается отскок цены в сторону основного тренда, например, от уровня 0,382. Но цена может не дойти до него, развернувшись внутри затемненной области диапазона. Стоит ли открывать сделку? Или же это коррекция внутри коррекции?
- Продолжится ли движение цены после отскока от уровня 0,382 в сторону тренда по достижении уровня 0,236? Или же уровень выступит зоной консолидации?
Ответить на эти вопросы поможет индикатор стандартного отклонения.
Шаг 1. Предварительный анализ.
На графике валютной пары GBP/USD с таймфреймом М15 уменьшаем масштабирование и прорисовываем уровень поддержки для StdDev с периодом 20. Уровень строится визуально по минимумам. Также наносим на восходящий тренд сетку Фибоначчи. На всякий случай на график также нанесена SMA (25), которая может подсказать
Шаг 2. Анализ текущей ситуации, поиск предполагаемых точек открытия сделки.
Здесь видно, что после достижения ценой максимума наступает флет: ценовая линия долго движется вниз в сторону первого уровня коррекции, дважды касаясь его. Но коррекция слабая, что подтверждает StdDev — он движется горизонтально вдоль своего уровня поддержки ближе к нулю.
Возможны два варианта развития события:
- Цена все-таки пробьет уровень коррекции 0,236 и уйдет вниз. Сигналом на открытие сделки будет окончание коррекции на уровне 0,382.
- Цена оттолкнется от уровня 0,236 и уйдет вверх к прорисовке нового максимума.
Индикатор стандартного отклонения должен будет подсказать момент начала тренда.
Шаг 3. Открытие сделки.
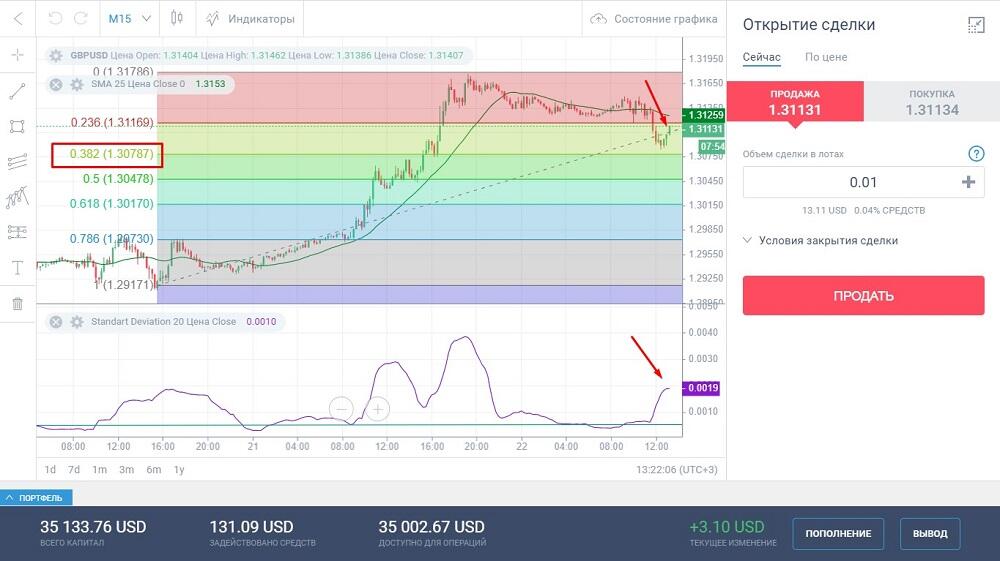
Дальше ситуация развивается следующим образом. Коррекция все-таки пробивает ключевой уровень 0,236 и уходит вниз. В этот момент StdDev начинает расти, но было бы ошибкой открывать короткую позицию по такому сигналу:
- StdDev не показывает направление тренда. Рост активности трейдеров означает только то, что цена вышла из флета, но она может развернуться в любой момент.
- Уровни коррекции Фибоначчи — ключевой индикатор, его сигналы основные.
Коррекция оканчивается, не дотянув до уровня 0,382, цена разворачивается вверх, StdDev растет. Открываем сделку.
Закрытие сделки по консервативному сценарию — достижение ценой ближайшего уровня Фибоначчи. В данном случае 0,236. Прибыль составила чуть более 7 долл. США за 30 минут.
FAQ по индикатору Standard Deviation
Что такое стандартное отклонение на форекс?
Усредненное значение отклонения цены от ее среднего арифметического за фиксированный период выборки. В Форексе стандартное отклонение — это индикатор изменчивости, который показывает, насколько сильно отклонилась цена от своего среднего значения. Увеличение стандартного отклонения означает рост волатильности. Инструмент позволяет определять начало, силу и момент разворота тренда, но не показывает его направление.
Как использовать индикатор Standard Deviation?
В качестве вспомогательного инструмента к трендовому индикатору и/или осциллятору на таймфреймах от М30-Н1 и выше. Сигналы на открытие сделки:
- На рынке наблюдается флет: цена на графике в боковике, просматриваются горизонтальные уровни сопротивления и поддержки.
- Цена пробивает уровень сопротивления или поддержки, закрываясь за пределами диапазона флета. На этой же свече или на следующей StdDev начинает расти.
- На следующей свече после сигнальной открываем сделку в сторону тренда.
Закрытие сделки в момент совпадения условий:
- Standard Deviation разворачивается вниз.
- На графике появилась свеча противоположного цвета.
Как рассчитать стандартное отклонение?
Пошаговый алгоритм расчета следующий:
- Рассчитать среднее арифметическое цен выборки, которое будет соответствовать значению простой средней скользящей.
- Из каждого значения цены выборки вычесть среднее арифметическое.
- Каждое полученное значение возвести в квадрат, все значения просуммировать. Затем разделить на количество членов в выборке, то есть на количество свечей.
- Из полученного результата извлечь квадратный корень.
Когда следует использовать индикатор Standard Deviation?
Чаще всего индикатор используется в качестве вспомогательного в трендовых стратегиях Forex. StdDev следует использовать в момент флета для поиска начала сильного трендового движения. Момент увеличения отклонения текущего значения цены от среднего значения с выходом цены из флетового диапазона — сигнал на открытие сделки. Разворот StdDev на своем максимуме может говорить о снижении активности трейдеров — сигнал на закрытие сделки.
Что означает высокое стандартное отклонение?
Цена максимально отклонилась от своего среднего значения за фиксированный период, расстояние от текущей цены до средней скользящей максимально. Это может говорить о том, что скоро активность трейдеров будет снижаться. Цена может вернуться к своему среднему значению или уйти во флет, тем самым перерисовав среднее значение заново.
P.S. Понравилась моя статья? Поделись ей в соцсетях, это лучшее спасибо 
Задавайте мне вопросы и комментируйте материал ниже. С удовольствием отвечу и дам необходимые пояснения.
Полезные ссылки:
- Торговлю с проверенным брокером рекомендую попробовать тут. Система позволяет торговать самостоятельно или копировать сделки успешных трейдеров со всего мира.
- Воспользуйтесь моим промокодом BLOG для получения бонуса 50% на депозит от LiteFinance. Промокод нужно просто ввести в соответствующее поле при пополнении счета в платформе LiteFinance и бонус зачислится одновременно с депозитом.
- Чат трейдеров в телеграм: https://t.me/marketanalysischat. Делимся сигналами и опытом.
- Канал в телеграм с отличной аналитикой, форекс обзорами, обучающими статьями и прочими полезностями для трейдеров: https://t.me/forexandcryptoanalysis
Содержание данной статьи является исключительно частным мнением автора и может не совпадать с официальной позицией LiteFinance. Материалы, публикуемые на данной странице, предоставлены исключительно в информационных целях и не могут рассматриваться как инвестиционный совет или консультация для целей Директивы 2004/39 /EC.
Оцените данную статью:
{{value}}
( {{count}} {{title}} )

























![Rendered by QuickLaTeX.com [ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3916a3ccd97d909589dfe1dabb970af0_l3.png)