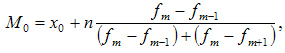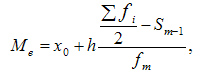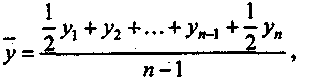Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.
После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.
Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.
Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.
В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.
Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.
Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.
Может еще поучимся? Загляни сюда!
Средняя хронологическая
Краткая теория
Средняя хронологическая — это средний
уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений
показателя в разные моменты или периоды времени. В зависимости от вида ряда
динамики применяются различные способы ее расчета, а именно расчет средней
хронологической интервального ряда и средней хронологической моментного ряда.
Ряды динамики состоят из числовых значений двух показателей:
моментов или периодов времени t, к которым относятся приводимые данные, и
соответствующих им статистических данных у, которые называются уровнями
динамического ряда. В зависимости от того, к моментам или периодам времени
привязываются статистические данные, различают два вида рядов динамики:
моментные и интервальные.
Когда уровни ряда динамики характеризуют размеры общественных
явлений за определенные интервалы (периоды) времени (за сутки, месяц, квартал,
год и т. п.), то такие ряды называются интервальными (или периодическими). В
отличие от моментного ряда динамики уровни интервального ряда динамики могут
быть суммированы. Например, сложив данные выпуска станков за четыре квартала,
можно получить показатель их выпуска за год.
Для интервальных рядов с равноотстоящими уровнями средняя
хронологическая имеет вид средней арифметической простой:
где
– уровни интервального ряда
— количество равных периодов времени
В интервальных рядах с неравноотстоящими
уровнями средняя хронологическая имеет вид средней
арифметической взвешенной:
где
– периоды времени, отделяющие один уровень
ряда от другого
Если уровни ряда динамики выражают состояние явления на
определенные моменты времени или даты, то такие ряды называют моментными рядами
динамики. Особенность моментного ряда динамики в том, что некоторые его уровни
содержат элементы повторного счета, т. е. каждый последующий уровень полностью
или частично включает в себя предыдущий уровень. Поэтому суммирование уровней
моментного динамического ряда не имеет смысла, но разность уровней имеет
определенное значение.
В моментном ряду динамики с равноотстоящими уровнями средняя хронологическая
имеет вид:
Средний уровень моментного ряда динамики с неравноотстоящими
уровнями характеризует средняя хронологическая взвешенная, которая исчисляется
по формуле:
где
и
– значение уровня моментного ряда динамики и
уровня, следующего за ним;
–
промежуток времени между датами.
Примеры решения задач
Задача 1
Остатки
готовой продукции на складе составили, тыс.руб.:
| Дата |
Остатки готовой продукции, тыс.руб. |
| 01.04.2011 | 506 |
| 01.05.2011 | 519 |
| 01.06.2011 | 587 |
| 01.07.2011 | 624 |
| 01.08.2011 | 624 |
| 01.09.2011 | 545 |
| 01.10.2011 | 580 |
| 01.11.2011 | 542 |
| 01.12.2011 | 576 |
| 01.01.2012 | 606 |
Требуется:
Определить средние остатки готовой
продукции на складе за II квартал, за III квартал, за IV квартал, за второе
полугодие 2011 года.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Средние
остатки продукции можно вычислить по формуле средней хронологической, так как
нам дан динамический моментный ряд с
равноотстоящими интервалами.
Средние
остатки за 2-й квартал:
Средние
остатки за 3-й квартал:
Средние
остатки за 4-й квартал:
Средние
остатки готовой продукции за второе полугодие:
Вывод
Таким
образом средние остатки готовой продукции за 2-й
квартал составили 557 тыс.р., за 3-й квартал 590,3 тыс.р., а за 4-й квартал 570,3 тыс.р.
Средние остатки готовой продукции за 2-е полугодие составили 580,3 тыс.р.
Задача 2
Известны
следующие данные об изменениях в списочном составе работников банка за январь,
человек.
| Число сотрудников | |
| Состояло по списку на 1 января | 205 |
| на 9 января | 200 |
| на 12 января | 198 |
| на 16 января | 201 |
| на 19 января | 197 |
| на 27 января | 199 |
| Состояло по списку на 1 февраля | 199 |
Определите
среднюю списочную численность работников банка в январе.
Решение
Данный
динамический ряд моментный, с неравноотстоящими датами.
Средняя
хронологическая взвешенная:
Вывод
Среднесписочная
численность работников банка в январе составила 200,2 чел.
Задача 3
Имеются
следующие данные о производстве молока в России за 1995-2000 годы (млн.т.)
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 39.2 | 35.8 | 34.1 | 33.3 | 32.3 | 32.3 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с равноотстоящими уровнями, то средний уровень исследуемого динамического
ряда найдем по формуле средней арифметической:
Вывод
Среднегодовое
производство молока в исследуемом периоде составило 34,5 млн. тонн.
Задача 4
Имеются
следующие данные о производстве продукции на заводе (млн. руб.)
| 2005 | 2008 | 2010 | 2011 | 2013 | 2014 |
| 45,4 | 48,3 | 41,5 | 39,6 | 42,5 | 46,8 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с неравноотстоящими уровнями, то средний уровень
исследуемого динамического ряда найдем по формуле средней арифметической
взвешенной:
Вывод
Среднегодовое производство продукции на предприятии в исследуемом
периоде составило 44,8 млн. рублей.
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
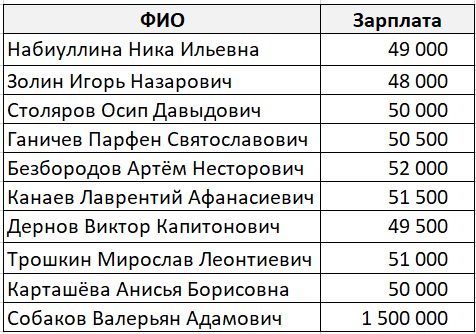
Давайте обратимся к классическому примеру со средней зарплатой.
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Формула:
- x – среднее арифметическое;
- xn – конкретное значение;
- n – количество значений.
Плюсы:
- Хорошо работает при нормальном распределении значений в выборке;
- Легко вычислить;
- Интуитивно понятно.
Минусы:
- Не дает реального представления о распределении значений;
- Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Формула:
- M0 – мода;
- x0 – нижняя граница интервала, который содержит моду;
- n – величина интервала;
- fm– частота (сколько раз в ряду встречается то или иное значение);
- fm-1 – частота интервала предшествующего модальному;
- fm+1 – частота интервала следующего за модальным.
Плюсы:
- Прекрасно подходит для получения представления об общественном мнении;
- Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
- Проста для понимания.
Минусы:
- Моды может просто не быть (нет повторов);
- Мод может быть несколько (многомодальное распределение).
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Формула:
- Me – медиана;
- x0 – нижняя граница интервала, который содержит медиану;
- h – величина интервала;
- f i – частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 – сумма частот интервалов предшествующих медианному;
- fm – число значений в медианном интервале (его частота).
Плюсы:
- Дает самую реалистичную и репрезентативную оценку;
- Устойчива к выбросам.
Минусы:
- Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
СРЗНАЧ(число1;[число2];…)— функция для определения среднего арифметического;МОДА.ОДН(число1;[число2];...)— функция моды (в более старых версиях Excel использоваласьМОДА(число1;[число2];...));МЕДИАНА(число1;[число2];...)— функция для поиска медианы.
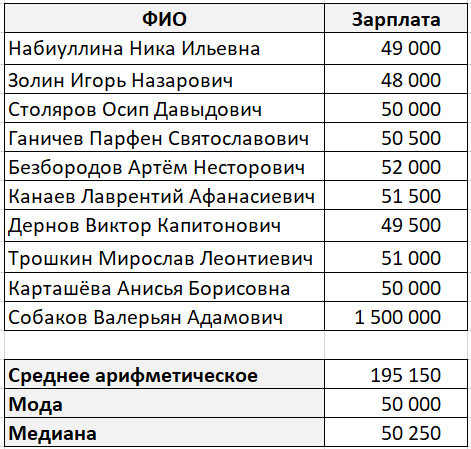
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.
И чтобы ее использовать достаточно написать вот такой запрос:
/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */ SELECT AVG(salary) AS 'Средняя зарплата' FROM employees
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Напишем запрос:
/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */ SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты' FROM employees GROUP BY salary ORDER BY COUNT(*) DESC
Вычисляем медиану на SQL
Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.
Выглядит все это так:
/* В данном случае процентиль 0.5 и будет являться медианой */
SELECT TOP(1) PERCENTILE_CONT(0.5)
WITHIN GROUP (ORDER BY salary)
OVER() AS 'Медианная зарплата'
FROM employees
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
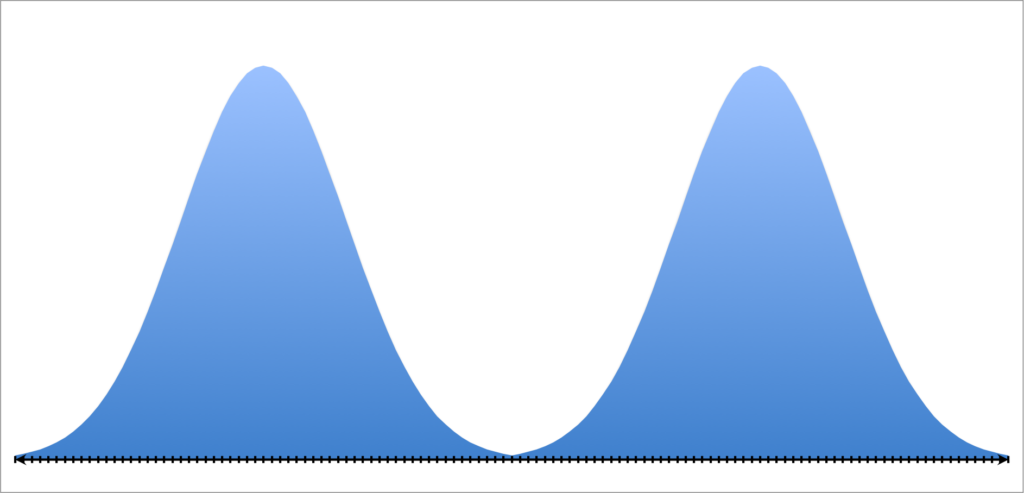
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Полезные ссылки:
- SQL и теория вероятностей (YouTube)
- Анализ нормальности распределения данных (YouTube)
- Меры центральной тенденции
- Об авторе
- Свежие записи
Добавить в «Нужное»
Средняя величина активов: формула по балансу
При исследовании результатов деятельности организации и анализе эффективности работы используются показатели как на конкретную дату, так и за определенный период времени. Эти показатели могут использоваться для расчета различного рода коэффициентов. Например, рентабельность активов определяется путем деления прибыли за период к стоимости активов. Однако было бы не совсем корректно относить прибыль, например, за год к величине активов на конец года, ведь тогда не учитывается динамика активов в течение года. Чтобы «смягчить» колебания величины активов на конкретную дату, рассчитывается их средняя величина. И в формуле рентабельности активов прибыль делится не на стоимость активов на конкретную дату, а на среднюю величину активов. Аналогично, коэффициент оборачиваемости активов определяется путем деления выручки за период на среднюю величину активов за этот же период. О том, как найти среднюю величину активов по балансу, расскажем в нашем материале.
Средняя величина активов это …
Варианты определения средней величины активов могут быть различные. Простейший вариант средней величины активов – это среднее арифметическое от их стоимости на начало и конец года.
Однако средняя величина может определяться и иначе.
Напомним, к примеру, как рассчитывается по итогам года средняя стоимость имущества, признаваемая объектом налогообложения по налогу на имущество (п. 4 ст. 376 НК РФ):
ИСГ = (ОС01.01 + ОС01.02 + ОС01.03 + … + ОС01.12 + ОС31.12) / 13,
где ОС01.01, ОС01.02, ОС01.03, …ОС01.12, ОС31.12 – остаточная стоимость имущества на 01.01, 01.02, 01.03, …01.12, 31.12 текущего года соответственно.
Таким образом, для определения средних активов формула будет зависеть от того, насколько высока частотность тех или иных усредняемых данных: показатели могут быть как ежедневные, так и ежеквартальные и т.д.
Однако для целей анализа баланса среднегодовая стоимость активов определяется как среднее из их значений на начало и конец года.
Средняя величина активов в балансе
Среднегодовая величина активов в балансе (АСГ) определяется по формуле (Приказ Минфина от 02.07.2010 № 66н):
АСГ = (стр.1600НГ + стр.1600КГ) / 2,
где стр.1600НГ – сумма по строке 1600 на 31.12 предшествующего года;
стр.1600КГ – сумма по строке 1600 на 31.12 отчетного года.
В то же время, по балансу может отдельно рассчитывается средняя величина отдельных групп или видов активов. К примеру, средняя величина внеоборотных активов или среднее значение запасов и т.д.
12
Наряду с абсолютными
и относительными величинами в статистике
большое применение находят средние
величины. В
повседневной жизни употребляются
термины «в среднем», «средняя».
Например, средняя цена, средний расход
продуктов, средняя заработная плата,
средняя мощность оборудования, средняя
выработка, средний размер сбережений
и т. д.
В экономическом
анализе часто приходится оперировать
средними величинами в целях лучшего
понимания общей картины, когда нужно
из многих признаков получить величину,
в которой отражались бы свойства всех
признаков, входящих в состав совокупности.
Средняя величина
в С — обобщающий показатель,
характеризующий типичный уровень
явления в конкретных условиях места
и времени, отражающий величину
варьирующего признака в расчете на
единицу качественно однородной
совокупности.
Средняя величина есть обобщающая
количественная характеристика однородных
явлений по какому-либо варьирующему
признаку.
Применение средних
величин позволяет охарактеризовать
определенный признак совокупности
одним числом, несмотря на количественные
различия единиц по данному признаку
внутри совокупности.
Следовательно,
средняя величина есть обобщающая
характеристика совокупности; средняя
величина выражает типичное свойство
совокупности; средняя величина —
величина абстрактная, а не конкретная,
так как в ней сглаживаются отдельные
значения единиц совокупности, имеющие
отклонения в ту и другую сторону;
реальность средней величины достигается,
если она вычисляется из одной совокупности.
Пользуясь средними
величинами при анализе массовых явлений,
необходимо всегда помнить, что часто в
средней величине скрываются отстающие
хозяйствующие субъекты, которые имеют
низкие показатели своей деятельности
и, наоборот, не выявляются фирмы, компании,
предприятия и т. д., которые работают
весьма эффективно. Это возможно, как
уже говорилось выше, в связи со свойством
средней, в которой отклонения отдельных
значений признака от ее величины взаимно
погашаются. (Так, например, при условии
выполнения плана розничного товарооборота
в целом по холдингу, занимающемуся
продажей товаров, часть фирм, входящих
в него, не выполнила план и, наоборот,
другая часть перевыполнила план
товарооборота.) Поэтому, кроме средней,
следует использовать и отдельные
индивидуальные показатели работы фирм,
входящих в холдинг.
В эк. практике
исп.-ся широкий круг показателей,
вычисленных в виде средних величин.
Напр, обобщающим
показателем доходов рабочих АО служит
средний доход одного рабочего, определяемый
отношением фонда з/п и выплат социального
характера за рассматриваемый период
(год, квартал, месяц) к численности
рабочих АО.
Вычисление
среднего – один
из распространенных приемов обобщения;
средний показатель отражает то общее,
что характерно (типично) для всех единиц
изучаемой совокупности, в то же время
он игнорирует различия отдельных
единиц. В каждом явлении и его развитии
имеет место сочетание случайности
и необходимости.
При исчислении средних в силу действия
закона больших чисел случайности
взаимопогашаются, уравновешиваются,
поэтому можно абстрагироваться от
несущественных особенностей явления,
от колич. значений признака в каждом
конкретном случае. В способности
абстрагироваться от случайности
отдельных значений, колебаний и
заключена научная
ценность средних как обобщающих
характеристик совокупностей.
Там, где возникает
потребность обобщения, расчет таких
характеристик приводит к замене множества
различных инд. значений признака средним
показателем, характеризующим всю
совокупность явлений, что позволяет
выявить закономерности, присущие
массовым общ. явлениям, незаметные в
единичных явлениях.
Средняя отражает
характерный, типичный, реальный уровень
изучаемых явлений, характеризует эти
уровни и их изменения во времени и в
пространстве; это сводная характеристика
закономерностей процесса в тех условиях,
в к-рых он протекает.
Выбор
вида средней
определяется эк. содержанием
определенного показателя и исходных
данных.
1)- Класс
степенных средних
— арифметическая,
гармоническая, геометрическая,
квадратическая, кубическая
и т.д. Помимо
степенных средних в с/практике используются
2) Структурные
средние —
применяются для изучения внутреннего
строения и структуры рядов распределения
значений признака. К таким показателям
относятся мода
и медиана..
Средняя хронологическая
Средняя
хронологическая — это средний уровень
ряда динамики, т. е.
средняя,
исчисленная по совокупности значений
показателя в разные моменты или периоды
времени. В
зависимости от вида ряда динамики
применяются различные способы ее
расчета, а именно расчет средней
хронологической интервального ряда и
средней хронологической моментного
ряда.
Средней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле
где
— средний уровень ряда;
у
— уровень ряда динамики;
n
— число членов ряда.
Средней
хронологической моментного ряда является
средняя величина из уровней моментного
ряда динамики.
Если f(t)
есть функция, выражающая изменение
моментного показателя во времени, то
за время (t)
от а
до b
средняя хронологическая моментyого
ряда равна:
Однако данных
непрерывного наблюдения значения f(t)
в распоряжении статистики, как правило,
нет. Поэтому в зависимости от характера
изменения показателя и имеющихся данных
применяются различные методы расчета.
При равных промежутках времени между
датами, на которые имеются данные, и
равномерном изменении размера показателя
между датами средняя хронологическая
моментного ряда обычно исчисляется
по формуле:
где у
— уровень ряда; n
— число всех
членов ряда;
—
средний уровень.
Если периоды
времени, отделяющие одну дату от другой,
не равны между собой, то расчет средней
хронологической моментного ряда
производится по формуле средней
взвешенной арифметической, в качестве
весов которой принимаются отрезки
времени между датами, т. е. по формуле:
гдеТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.
Известно, например,
что в январе 2007 года произошло следующее
изменение численности сотрудников
компании «Бест»: было на 1 января
551 чел., уволился 2 января один сотрудник,
было принято 6 января 24 человека, 16
января— 6 человек, уволилось 25 января—
10 сотрудников. Требуется определить
среднюю численность сотрудников компании
«Бест» в январе 2007 г. Рассчитаем
число календарных дней, в течение которых
численность сотрудников компании «Бест»
оставалась без изменения, и произведение
этих чисел.
Таблица 5
Данные для расчета средней численности сотрудников компании «Бест»
|
Численность |
Число |
Произведение |
|
551 |
1 |
551 |
|
550 |
4 |
2200 |
|
574 |
10 |
5740 |
|
580 |
9 |
5220 |
|
570 |
7 |
3990 |
|
ИТОГО |
31 |
17701 |
Используя данные
произведенных расчетов, получим:
В отличие от первого
способа расчета средней хронологической
моментного ряда второй способ дает
точное значение средней.
Средняя гармоническая (сг).
СГ применяется
в тех случаях, когда частоты (веса) не
приводятся непосредственно, а входят
сомножителями в один из имеющихся
показателей.
Пример. Автомобиль
доставил товары в три магазина фирмы
«Весна», которые удалены от головного
предприятия на одинаковое расстояние.
Так, до первого магазина, расположенного
на шоссейной дороге, автомобиль прошел
путь со скоростью 50 км/ч, до второго, по
проселочной дороге, — 40 км/ч, а в третьем
случае автомобилю пришлось полпути
пройти через лесной массив, и скорость
движения составила только 30 км/ч.
Требуется определить
среднюю скорость движения автомобиля.
На первый взгляд представляется, что
средняя скорость • движения может быть
определена по формуле простой
арифметической:
Однако нетрудно
убедиться, что средняя вычислена
неправильно. В самом деле, производя
расчет средней скорости по простой
арифметической средней, исходим из
того, что автомобиль во всех трех случаях
прошел одинаковое расстояние, пройдя
соответственно 50, 40 и 30 км, т. е. всего
120 км. Если бы условие этой задачи
было сформулировано в такой форме, то
средняя была бы рассчитана правильно
и характеризовала бы пройденное
автомобилем среднее расстояние.
В действительности
же эта средняя рассчитана неверно, так
как «в условия задачи не следует, что
автомобиль на преодоление расстояния
до трех магазинов фирмы «Весна»
проехал 120 км, так как Скорость движения
была различная. Следовательно, он прошел
и разное расстояние.
В тех случаях,
когда вес каждого варианта равен единице
(индивидуальные значения обратного
признака встречаются по одному разу),
применяется СГ
простая,
исчисляемая по формуле:
где x
– отдельные варианты обратного
признака, встречающиеся по одному разу;
n–
число вариантов.
(8)

в сокращенном виде
где
—средняя
гармоническая;
—
числа, обратные заданным вариантам.
Иначе говоря, СГ
простая
отношение числа вариантов к сумме
обратных значений этих вариантов.
Для нашего примера
будем иметь:
В нашем примере
СА (ха)
оказалась
больше средней гармонической
.
При этом абсолютная
ошибка завышения составляет
— 2 км/ч (38 — 40), а относительная —5%
Т.о., неправильное
использование СА привело бы к завышению
средней скорости движения автомобиля
и к неправильному определению объема
перевозок. Это еще раз доказывает, с
какой осторожностью следует решать
вопрос о том, какую среднюю надлежит
применять в экономических расчетах.
В рассмотренном
примере частоты (веса) имели одно значение
и равнялись единице. Если же частоты
(веса) различные, то применяется СГ
взвешенная, которая
вычисляется следующим образом:
Где
—
СГ взвешенная:
Как первая, так и
вторая формулы показывают, что СГ есть
величина обратная СА.
Веса арифметической
средней и гармонической средней
обозначены разными буквами: f
и m.
Это не случайно, так как весами СА служат
частоты рассматриваемого ряда, а весами
СГ будет произведение вариантов на
веса.
Пример.
Рассмотрим данные о реализации товаров
по двум магазинам фирмы «Весна»
(табл. 6). Таблица
.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.05.20153.63 Mб107. Лекц.БУ-анализ.doc
- #
18.12.2018130.46 Кб297.docx