Задачи по статистике с решением — Средние величины
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:


|
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
|
1 2 3 4 5 |
18 18 19 20 19 |
6 7 8 9 10 |
20 19 19 19 20 |
11 12 13 14 15 |
22 19 19 20 20 |
16 17 18 19 20 |
21 19 19 19 19 |
Если сгруппировать данные, то получим ряд распределения:


2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт., Хi |
18 |
19 |
20 |
21 |
22 |
Всего |
|
Число рабочих, fi |
2 |
11 |
5 |
1 |
1 |
20 |


3. Задача на вычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет. |
Число рабочих, чел., fi |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
ИТОГО: |
200 |


4. Задача на вычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
|
Группы рабочих по оплате труда у.е. |
Число рабочих, чел. |
Середина интервала, хi |
|
До 500 |
5 |
450 |
|
500-600 |
15 |
550 |
|
600-700 |
20 |
650 |
|
700-800 |
30 |
750 |
|
800-900 |
16 |
850 |
|
900 и более |
14 |
950 |
|
Итого: |
100 |
— |

Задача 5. Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий |
Середина интервалов, х |
|
Хi*f |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
Итого: |
25 |
— |
— |
0 |
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i— величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I, получим новый вариационный ряд распределения новых вариантов хi. Средняя арифметическая их новых вариантов- момент первого порядка m i= 

Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
|
Предприятие |
Численность промышленно- производственного персонала, чел |
Месячный фонд заработной платы, тыс руб. |
Средняя заработная плата, руб. |
|
А |
1 |
2 |
3 |
|
1 2 3 |
540 275 458 |
564,84 332,75 517,54 |
1046 1210 1130 |
|
ИТОГО: |
1 273 |
1415,13 |
? |
Определить среднюю з/п по всем предприятиям.
Решение:
Составим логическую формулу средней: средняя з/п по всем предприятиям =
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной:

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.


3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
|
№ магазина |
Цена моркови., руб за кг. |
Выручка от реализации, руб. |
|
1 2 3 |
17 20 24 |
3060 2800 1920 |
|
Итого: |
— |
7780 |
Решение.
Логическая формула средней: средняя цена моркови =
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
|
Вид вклада |
Октябрь |
Ноябрь |
||
|
Число вкладов, тыс., f |
Средний размер вклада, руб., x |
Сумма вкладов, млн. руб., F |
Средний размер вклада, x |
|
|
До востребования Срочный |
10 8 |
350 400 |
4,07 3,87 |
370 430 |
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:


2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:


2) решение по средней арифметической взвешенной



Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3)
Сущность
средней заключается в том, что в ней
взаимопогашаются отклонения значений
признака отдельных единиц совокупности,
обусловленные действием случайных
факторов, и учитываются изменения,
вызванные действием факторов основных.
Это позволяет средней отражать типичный
уровень признака и абстрагироваться
от индивидуальных особенностей, присущих
отдельным единицам. Типичность средней
непосредственным образом связана с
однородностью статистической совокупности.
Средняя величина только тогда будет
отражать типичный уровень признака,
когда она рассчитана по качественно
однородной совокупности.
Средняя
арифметическая простая (невзвешенная):
Средняя
арифметическая взвешенная:
В
отдельных случаях веса могут быть
представлены не абсолютными величинами,
а относительными (в процентах или долях
единицы). В этом случае применяется
средняя гармоническая взвешенная:

где.
При
расчете средней по интервальному
вариационному ряду
—
середина интервала. При этом величины
открытых интервалов (первого и последнего)
условно приравниваются к величинам
интервалов, примыкающих к ним (второго
и предпоследнего).
Средняя
геометрическая невзвешенная:
Средняя
геометрическая взвешенная:
Средняя
квадратическая невзвешенная:
Средняя
квадратическая взвешенная:
Наряду
с рассмотренными средними величинами
в качестве статистических характеристик
вариационных рядов распределения
рассчитываются так называемые структурные
средние мода и медиана.
Мода
()
представляет собой значение изучаемого
признака, повторяющееся с наибольшей
частотой. Медианой ()
называется значение признака, приходящееся
на середину ранжированной (упорядоченной)
совокупности.
Мода
для дискретных рядов распределения
отыскивается сразу (по максимальной
частоте). Для определения медианного
значения признака находят номер медианной
единицы ряда ():
,
где— объем совокупности.
Определение
моды и медианы по интервальным рядам
требует проведения расчетов на основе
следующих формул:
где
xMo
– начальное значение модального
интервала,
iMo
– величина модального интервала,
fMo
– частота модального интервала,
fMo-1
–
частота интервала, предшествующего
модальному
fMo+1
– частота интервала, следующего за
модальным .
где
хМе
— начальное
значение медианного интервала
iMe
— величина
медианного интервала
SMe-1
– сумма
накопленных частот, предшествующих
медианному интервалу
fMe
– частота медианного интервала.
Решение типовых задач.
№1.
По
имеющимся данным о ценах товара в
различных фирмах города определить
среднюю цену: 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6
4,1
Решение:
№2.
Определить
среднее количество филиалов банка
|
Количество |
Число |
xf |
Частость, |
xw |
|
2 |
1 |
2 |
0,05 |
0,1 |
|
3 |
5 |
15 |
0,25 |
0,75 |
|
4 |
8 |
32 |
0,4 |
1,6 |
|
5 |
4 |
20 |
0,2 |
1 |
|
6 |
2 |
12 |
0,1 |
0,6 |
|
Итого |
20 |
81 |
1 |
4,05 |
Решение:
Для
расчета заполним столбец хf,
и
рассчитаем итог по столбцу:
.
Используя
свойства средней арифметической, для
расчета вместо частот можно использовать
значения частостей:
.
№3.
Рассчитать
средний размер прибыли банка.
|
№ группы |
Размер |
Число |
x/ |
x/f |
||
|
1 |
3,7 |
— |
4,6 |
3 |
4,15 |
12,45 |
|
2 |
4,6 |
— |
5,5 |
3 |
5,05 |
15,15 |
|
3 |
5,5 |
— |
6,4 |
7 |
5,95 |
41,65 |
|
4 |
6,4 |
— |
7,3 |
4 |
6,85 |
27,4 |
|
5 |
7,3 |
— |
8,2 |
3 |
7,75 |
23,25 |
|
Итого |
20 |
119,9 |
Решение:
млн.
руб.
При
расчете можно, так же, как в предыдущем
случае, воспользоваться значениями
частостей.
№4.
По
трем обменным пунктам известен курс
доллара и выручка от продажи валюты.
Рассчитать средний курс доллара по этим
обменным пунктам.
|
Номер |
Валютный х |
Выручка В |
|
1 |
28,70 |
232,47 |
|
2 |
28,68 |
298,27 |
|
3 |
28,73 |
149,40 |
|
Итого |
680,14 |
Решение:
Статистическая
информация не содержит частот по
отдельным вариантам, а представлена
как их произведение, поскольку выручка
от продажи валюты – это произведение
валютного курса (х)
на объем продаж. Поэтому применим формулу
средней гармонической взвешенной.

№5.
Двое
рабочих в течение рабочего дня заняты
изготовлением одинаковых деталей. Один
рабочий тратит на изготовление детали
3 минуты, другой – 6 мин. Определить
средние затраты времени на изготовление
детали.
Решение:
Применение
формулы средней арифметической простой
приведет к неправильному результату,
т.к. в течение рабочего дня ими было
изготовлено разное число деталей.
Затраты
времени представляют собой произведение
количества изготовленных деталей (f)
и времени на изготовление одной детали
(x).
Поскольку затраты рабочего времени
(xf)
у обоих рабочих равны (рабочий день), то
применим формулу средней гармонической
простой.
Итак,

№6.
По
имеющимся данным о ценах товара в
различных фирмах города определить
моду и медиану.
а)
4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6
б)
4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 4,1
Решение:
В
обоих случаях данные не сгруппированы.
а)
в данной совокупности чаще всего
повторяется значение 4,3, поэтому Мо=4,3
Для
определения медианы надо провести
ранжирование:
4,2
4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6
В
данном ряду нечетное число членов,
варианта, расположенная посередине,
является медианой. Ме=4,4
б)
в данной совокупности чаще всего
повторяется значение 4,3, поэтому Мо=4,3
Для
определения медианы проведем ранжирование:
4,1
4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6
В
данном ряду четное число членов (10),
поэтому медиана рассчитывается как
средняя арифметическая из двух вариант,
расположенных в центре ряда, т.е.
Ме=(4,3+4,4)/2=4,35
№7.
По имеющимся данным определить моду и
медиану
|
Количество |
Число f |
Накопленные |
|
2 |
1 |
1 |
|
3 |
5 |
6 |
|
4 |
8 |
14 |
|
5 |
4 |
|
|
6 |
2 |
|
|
Итого |
20 |
Решение:
Данные
представлены в виде дискретного ряда
распределения.
Наибольшая
частота f=8
соответствует варианте х=4,
поэтому Мо
= 4.
Для
нахождения медианы следует рассчитать
накопленные частоты. S=14,
впервые превысившая 10 (половину общей
суммы частот), соответствует варианте
х=4.
Значит, Ме=4.
№8.
По
имеющимся данным определить моду и
медиану
-
№ группы
Размер
прибыли,
хЧисло
банков (частота)
fНакопленные
частоты
S1
3,7
— 4,63
3
2
4,6
— 5,53
6
3
5,5
— 6,47
13
4
6,4
— 7,34
5
7,3
— 8,23
Итого
20
Решение:
Данные
представлены в виде интервального ряда
распределения ряда распределения.
Для
расчета моды требуется сначала определить
модальный интервал: наибольшая частота
f=7
соответствует интервалу 5,5 — 6,4. Значит,
это модальный интервал. Конкретное
значение моды определяется по формуле:
Для
расчета медианы определим медианный
интервал. Для этого рассчитаем накопленные
частоты, пока они не превысят половину
суммы частот (т.е. 10). S=13
соответствует интервалу 5,5 — 6,4, значит,
это медианный интервал. Конкретное
значение медианы найдем по формуле:
Соседние файлы в папке Статистика
- #
- #
- #
- #
Средняя арифметическая взвешенная и средняя гармоническая
Краткая теория
В процессе обработки и обобщения статистических
данных возникает необходимость определения средних величин. Как правило,
индивидуальные значения одного и того же признака у различных единиц
совокупности неодинаковы. Средняя величина — обобщающая характеристика
изучаемого признака в исследуемой совокупности. Она отражает его типичный
уровень в расчете на единицу совокупности в конкретных условиях места и
времени. Например, при изучении доходов рабочих концерна обобщающей
характеристикой служит средний доход одного рабочего. Для его определения общую
сумму средств, направленных на потребление, в виде заработной платы, социальных
и трудовых льгот, материальной помощи, дивидендов по акциям и процентов по
вкладам в имущество концерна за рассматриваемый период (год, квартал, месяц)
делят на численность рабочих концерна.
Очень важное правило — вычислять средние величины
лишь по однородной совокупности единиц. Только при выполнении этого условия
средняя как обобщающая характеристика отражает общее, типичное, закономерное,
присущее всем единицам исследуемой совокупности. Прежде чем вычислять средние
величины, необходимо произвести группировку единиц исследуемой совокупности,
выделив качественно однородные группы.
Средняя, рассчитанная по совокупности в целом,
называется общей средней, средние, исчисленные для каждой группы, — групповыми
средними. Общая средняя отражает общие черты изучаемого явления, групповая
средняя дает характеристику размера явления, складывающуюся в конкретных
условиях данной группы. Сравнительный анализ групповых и общих средних
используется для характеристики социально-экономических типов изучаемого
общественного явления.
В статистике используются различные виды
средних величии: средняя арифметическая, средняя гармоническая, средняя
геометрическая, средняя квадратическая, средняя хронологическая и т. д. При
использовании средних величин важно правильно выбрать вид средней и способ ее
расчета. Самой распространенной средней, используемой в социально-экономическом
анализе, является средняя арифметическая.
Средние арифметические бывают простые и
взвешенные. Средняя арифметическая простая рассчитывается по формуле:
где
– индивидуальные значения признака, средняя величина
которых находится,
– количество единиц совокупности.
Средняя арифметическая простая
применяется в тех случаях, когда каждое индивидуальное значение признака
встречается один раз или одинаковое количество раз.
Если же варианты (значения признака)
встречаются неодинаковое количество раз, то используется средняя арифметическая взвешенная:
где
– варианты, значения признака,
– частота появления соответствующего значения
признака.
В некоторых случаях средняя
рассчитывается по другому – когда известен ряд вариант
и ряд произведений вариант на частоту
,
а сама частота
неизвестна. В этом случае средняя
рассчитывается по формуле средней гармонической взвешенной:
где
Средняя гармоническая может иметь и
простую форму расчета, которая в практике статистики используется крайне редко
и представляет собой простую среднюю из обратных значений признака.
Величина средних величин зависит как от
индивидуальных значений признака в случае использования простых видов средних величин,
так и от удельного веса этих значений в общей совокупности при использовании
взвешенных видов.
Формулы средних взвешенных применяются во
всех случаях, когда варианты значений признака имеют различный удельный вес, а
формулы простых (не взвешенных) средних — когда варианты имеют равные веса. В первом
случае расчет ведется по уже сгруппированным данным на основании дискретных рядов распределения, а во втором — обычно по несгруппированным, где каждый
признак представлен одним числом или равное число раз. Неправильный выбор
формулы, расчет средних показателей по формуле средней простой вместо средней
взвешенной может привести к серьезным ошибкам.
Средние
величины применяются для оценки достигнутого изучаемого показателя, при анализе
и планировании экономической деятельности предприятий. Средняя величина всегда
величина именованная и имеет ту же размерность что и признак у отдельных единиц
совокупности. Основным условием правильного расчета средней величины
является качественная однородность совокупностей, по которой исчислена средняя.
Примеры решения задач
Задача 1
Имеются
следующие данные о работе автотранспортных предприятий за отчетный период:
| № п/п | Общий грузооборот, млн.т/км |
Выполнено тыс. т/км в среднем на 1 автомобиль |
% выпуска автомобилей на линию |
Средняя грузоподъемность одного автомобиля, т |
В общем грузообороте доля его выполнения за пределы региона (%) |
| 1 | 39 | 130 | 71 | 6.2 | 32 |
| 2 | 57 | 156 | 85 | 5.9 | 45 |
| 3 | 41 | 127 | 79 | 5.5 | 28 |
Определите
по совокупности предприятий средние значения всех признаков, используя
экономически обоснованные формулы расчета. Укажите вид и форму рассчитанных
средних.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Средний
грузооборот вычислим по формуле средней арифметической простой:
Среднее
выполнение на 1 автомобиль тыс.т/км по формуле
средней гармонической, так как определяющим показателем в данном случае
является отсутствующее в условии число
автомобилей:
где
– общий грузооборот
– среднее выполнение на 1 автомобиль тыс.т/км
Средний
процент выпуска автомобилей на линию вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является численность автомобилей,
которую в свою очередь можно найти делением общего грузооборота на выработку
одного автомобиля.
– процент выпуска автомобилей на линию
– численность автомобилей
Среднюю
грузоподъемность одного автомобиля вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является численность автомобилей,
которую в свою очередь можно найти делением общего грузооборота на выработку
одного автомобиля.
– грузоподъемность 1 автомобиля
– численность автомобилей
Среднюю
долю выполнения за пределы региона вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является общий грузооборот.
– доля в общем грузообороте выполнения за
пределы региона
– общий грузооборот
Таким
образом средний грузооборот по предприятиям составил 45,7 млн. т/км, средняя
выработка на 1 автомобиль — 138,6 тыс.
т/км, средний процент выпуска
автомобилей на линию – 78,8%, средняя грузоподъемность одного автомобиля – 5,9
т., а средняя доля в общем грузообороте выполнения за пределы региона составила
36,2%.
Задача 2
Имеются
данные о финансовых показателях предприятий за отчетный период.
| Предприятия | Получено прибыли, тыс.руб. | Акционерный капитал, тыс.р. |
Рентабельность акционерного капитала, % |
| А | 1 | 2 | 3 |
| 1 | 1512 | 5040 | 30 |
| 2 | 528 | 1320 | 40 |
| 3 | 1410 | 5640 | 25 |
Определите
средний процент рентабельности акционерного капитала фирмы, используя
показатели:
- гр. 1
и гр. 2 - гр. 2
и гр. 3 - гр. 1
и гр. 3
Решение
1)
Средний процент рентабельности в этом случае определим напрямую, по формуле
рентабельности:
2)
Средний процент рентабельности в этом случае определим по формуле средней арифметической
взвешенной:
3)
Средний процент рентабельности в этом случае определим по формуле средней
гармонической:
Средний
процент рентабельности по всем предприятиям составил 28.75%
Задача 3
- Рассчитайте средние значения всех признаков, приведенных в условии
задачи. - Укажите формулу расчета средней в обозначениях задачи, расчет полностью,
вид и формулу средней, использованной в расчете, единицы измерения средней.
Имеются
следующие данные (данные условные):
| Страна | Стоимость экспорта РФ, млн.долл.США |
Доля экспорта в стоимости внешнеторгового оборота, % |
Доля морепродуктов в стоимости экспорта, % |
Доля мороженной рыбы в стоимости экспорта морепродуктов, % |
Средняя цена за тонну мороженной рыбы, долл. США |
| S | D | R | M | C | |
| Япония | 2995 | 74.8 | 5.46 | 74.2 | 1843 |
| Корея | 835 | 49.9 | 3.72 | 97.3 | 594 |
| Китай | 3981 | 76.0 | 0.56 | 97.1 | 478 |
| Индия | 2172 | 47.4 | 0.32 | 82.5 | 725 |
Решение
Среднюю
стоимость экспорта вычислим по формуле средней арифметической простой:
Среднюю
долю экспорта в стоимости внешнеторгового оборота вычислим по формуле средней
гармонической:
Среднюю
долю морепродуктов в стоимости экспорта вычислим по формуле средней
арифметической взвешенной:
Долю мороженной рыбы в стоимости экспорта морепродуктов вычислим
по формуле:
Среднюю
цену за тонну мороженной рыбы вычислим по формуле:
Вывод к задаче
Таким
образом средняя стоимость экспорта составила 2495,75 млн.долл.,
средняя доля экспорта в стоимости внешнеторгового оборота 64,4%, средняя доля
морепродуктов в стоимости экспорта 2.2%. Доля мороженной
рыбы в стоимости экспорта морепродуктов составила 79.9%, а средняя цена тонны
мороженной рыбы 1053.1 долл.
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Пример решения задачи. Виды средних величин
Условие задачи
Имеются следующие
данные о товарообороте трех магазинов за два периода:
| Номер магазина | I квартал | II квартал | ||
|
Фактический товарооборот, млн.р. |
Выполнение плана, % |
План по товарообороту, млн.р. |
Выполнение плана, % |
|
| 1 | 1200 | 100 | 1250 | 105 |
| 2 | 1400 | 110 | 1500 | 100 |
| 3 | 920 | 96 | 1100 | 105 |
Определите средний процент выполнения плана в целом по
трем магазинам за каждый квартал в
отдельности. Обосновать выбор вида средних, написать их формулы.
Решение задачи
Средняя гармоническая
Для вычисления среднего процента
за 1-й квартал используем среднюю гармоническую взвешенную, т.к. между данными существует обратная зависимость.
Средняя гармоническая взвешенная рассчитывается по формуле:
-выполнение
плана
-фактический товарооборот
Средняя арифметическая взвешенная
Для вычисления среднего процента выполнения плана за 2-й квартал применим
среднюю арифметическую взвешенную, т.к.
между показателями существует прямая зависимость.
— план товарооборота
-выполнение плана
Таким образом, во 2-м квартале
выполнение плана составляет 103,1%, в первом квартале этот показатель составлял
102,6%.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.













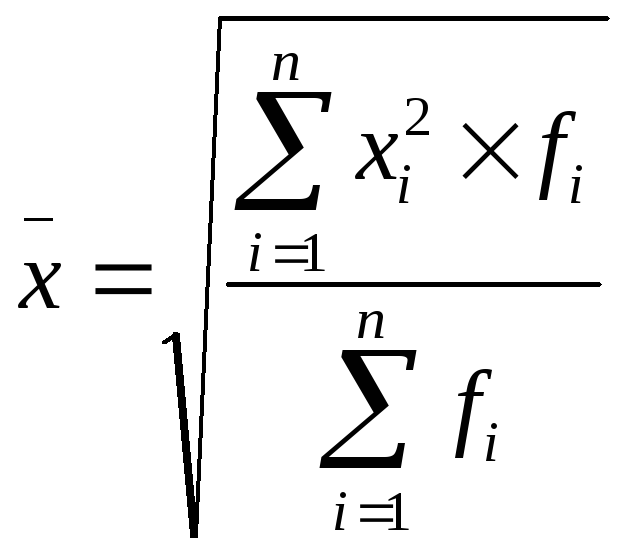


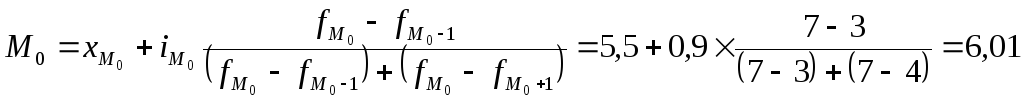



 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.



