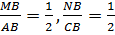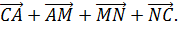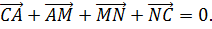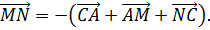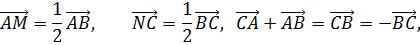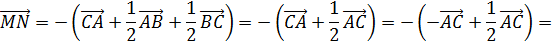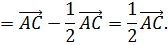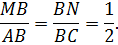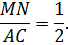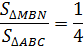Как найти среднюю точку в треугольнике

Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Определение средней линии треугольника

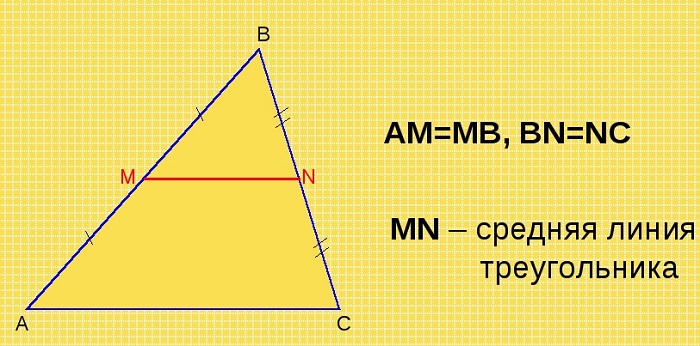
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

• KL – средняя линия треугольника ABC
• K – середина стороны AB: AK = KB
• L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

• △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
• Стороны △KBL в два раза меньше соответствующих сторон △ABC:
  AB = 2KB, BC = 2BL, AC = 2KL.
• S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.

Таким образом, средняя линия LM = 1 /₂ ⋅ BC = 1 /₂ ⋅ 10 = 5.

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Определение и признаки средней линии треугольника

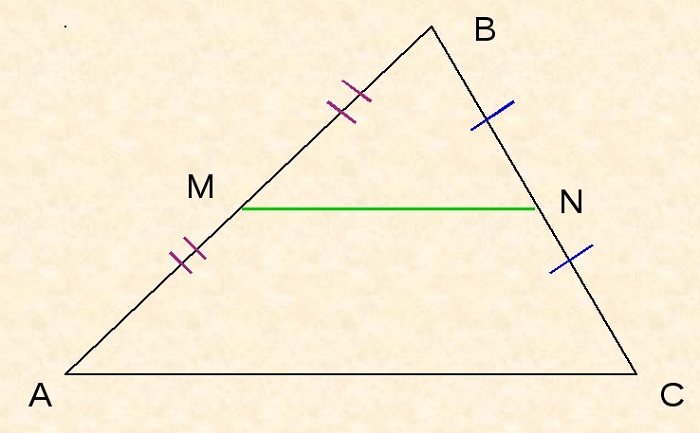
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Следствия из теоремы с доказательствами

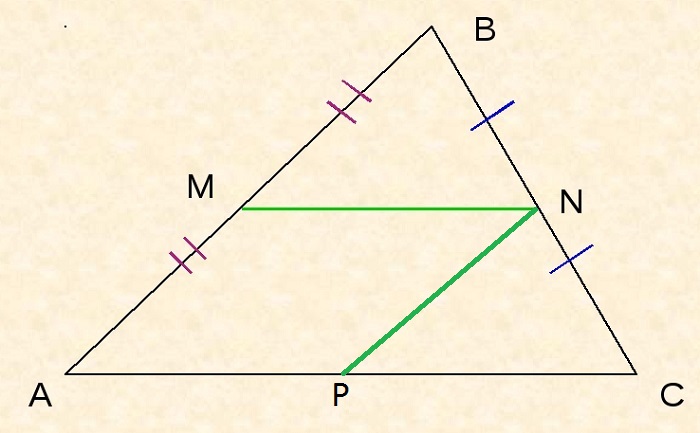
Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

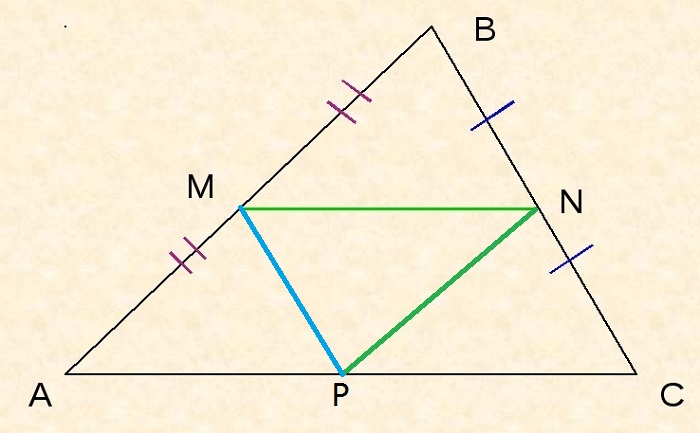
Следствие №2

Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Пример решения задачи

Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Уравнение средней линии

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

М — середина отрезка AB, N — середина BC.

Составим уравнение прямой MN, например, в виде y=kx+b:

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

— середина отрезка AB. Составим уравнение прямой AC:

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

то есть уравнение прямой MN ищем в виде

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

Таким образом, уравнение прямой MN

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Средняя точка сегмента (x 1, y 1) до (x 2, y 2)

В геометрии, средняя точка является средней точкой отрезок . Он находится на равноудалении от обеих конечных точек и является центроидом как сегмента, так и конечных точек. Он делит пополам сегмент.

Содержание

• 1 Формулы
• 2 Конструкция
• 3 Геометрические свойства, включающие средние точки
  • 3.1 Круг
  • 3.2 Эллипс
  • 3.3 Гипербола
  • 3.4 Треугольник
  • 3.5 Четырехугольник
  • 3.6 Общие многоугольники
• 4 Обобщения
• 5 См. Также
• 6 Ссылки
• 7 Внешние ссылки

Формулы

Середина сегмента в n-мерном пространстве, конечными точками являются A = (a 1, a 2,…, an) { displaystyle A = (a_ {1}, a_ {2}, dots, a_ {n})}и B = (b 1, b 2,…, b n) { displaystyle B = (b_ {1}, b_ {2}, dots, b_ {n})}определяется как

A + B 2. { displaystyle { frac {A + B} {2}}.}

То есть, координата i средней точки (i = 1, 2,…, n) равна

ai + bi 2. { displaystyle { frac {a_ {i} + b_ {i}} {2}}.}

Строительство

Учитывая две точки интереса, найти среднюю точку отрезка линии, который они определяют, можно выполняется с помощью компаса и линейки. Середину линейного сегмента, встроенного в плоскость , можно определить, сначала построив линзу , используя дуги окружности равного (и достаточно большого) радиуса с центрами в двух конечных точках, а затем соединение бугров линзы (две точки пересечения дуг). Точка, в которой линия, соединяющая выступы, пересекает сегмент, тогда является серединой сегмента. Сложнее найти середину, используя только компас, но это все же возможно в соответствии с теоремой Мора-Маскерони.

Геометрические свойства, включающие средние точки

Окружность

Средняя точка любого диаметра круга является центром круга.

Любая прямая , перпендикулярная любой хорде окружности и проходящая через ее среднюю точку, также проходит через центр окружности.

Теорема бабочка гласит, что если M является средней точкой хорды PQ окружности, через которую проходят две другие хорды AB и CD, то AD и BC пересекают хорду PQ в точке X и Y соответственно, так что M — середина XY.

Эллипс

Середина любого сегмента, который является биссектрисой области биссектрисы или периметром биссектрисы эллипса — центр эллипса.

Центр эллипса также является средней точкой сегмента, соединяющего два фокусировки эллипса.

Гипербола

Середина отрезка, соединяющего вершины гиперболы, является центром гиперболы.

Треугольник

Серединный перпендикуляр стороны треугольника — это линия, которая перпендикулярна этой стороне и проходит через ее середину. Три серединных перпендикуляра трех сторон треугольника пересекаются в центре описанной окружности (центр окружности, проходящей через три вершины).

медиана стороны треугольника проходит как через среднюю точку стороны, так и через противоположную вершину треугольника. Три медианы треугольника пересекаются в центроиде треугольника (точка, в которой треугольник балансировал бы, если бы он был сделан из тонкого листа металла однородной плотности).

центр из девяти точек треугольника находится в средней точке между центром описанной окружности и ортоцентром. Все эти точки находятся на линии Эйлера.

Середина (или средняя линия) треугольника — это отрезок прямой, который соединяет середины двух сторон треугольника. Он параллелен третьей стороне и имеет длину, равную половине этой третьей стороны.

Средний треугольник данного треугольника имеет вершины в серединах сторон данного треугольника, поэтому его стороны являются тремя средними сегментами данного треугольника. Он имеет тот же центр тяжести и медианы с данным треугольником. периметр среднего треугольника равен полупериметру (половине периметра) исходного треугольника, а его площадь составляет одну четверть площади исходного треугольника. ортоцентр (пересечение высот ) среднего треугольника совпадает с центром описанной окружности (центром круга, проходящего через вершины) исходного треугольника.

Каждый треугольник имеет начертанный эллипс, называемый его эллипсом Штейнера, который касается треугольника внутри в серединах всех его сторон.. Этот эллипс расположен в центре тяжести треугольника, и он имеет наибольшую площадь из всех эллипсов, вписанных в треугольник.

В прямоугольном треугольнике центр описанной окружности является средней точкой гипотенузы.

В равнобедренном треугольнике медиана, высота, а серединный перпендикуляр со стороны основания и биссектриса угла вершины совпадают с линией Эйлера и осью симметрии , и эти совпадающие линии проходят через середину стороны основания.

Четырехугольник

Два бимедиана выпуклого четырехугольника — это отрезки прямых, которые соединяют середины противоположных сторон, следовательно, каждая делит две стороны пополам. Две бимедианы и линейный сегмент, соединяющий середины диагоналей, являются параллельными в (все пересекаются в) точке, называемой «центроидом вершины», которая является средней точкой всех трех из этих сегментов.

Четыре «солодости» выпуклого четырехугольника — это перпендикуляры к стороне, проходящей через середину противоположной стороны, отсюда деление последней стороны пополам. Если четырехугольник циклический (вписан в круг), все эти солодости встречаются в общей точке, называемой «антицентром».

Теорема Брахмагупты утверждает, что если вписанный четырехугольник ортодиагонален (то есть имеет перпендикуляр диагоналей ), то перпендикуляр к стороне от точка пересечения диагоналей всегда проходит через середину противоположной стороны.

Теорема Вариньона утверждает, что середины сторон произвольного четырехугольника образуют вершины параллелограмма , и если четырехугольник не самопересекающийся, то площадь параллелограмма равна половине площадь четырехугольника.

Линия Ньютона — это линия, соединяющая середины двух диагоналей в выпуклом четырехугольнике, который не является параллелограммом. Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, пересекаются в точке, лежащей на линии Ньютона.

Общие многоугольники

A правильный многоугольник имеет вписанную окружность, которая касается каждой стороны многоугольника в его средней точке.

В правильном многоугольнике с четным числом сторон, середина диагонали между противоположными вершинами является центром многоугольника.

растягивающий до середины многоугольник циклического многоугольника P (многоугольник, все вершины которого лежат на одной окружности) — это еще один циклический многоугольник. вписанный в тот же круг, многоугольник, вершины которого являются серединами дуг окружности между вершинами P. Итерация операции растяжения средней точки на произвольном исходном многоугольнике приводит к последовательности многоугольников, формы которых сходятся к формула правильного многоугольника.

Обобщения

Вышеупомянутые формулы для средней точки сегмента неявно используют длины сегментов. Однако в обобщении до аффинной геометрии, где длины сегментов не определены, средняя точка все еще может быть определена, поскольку это аффинный инвариант. синтетическое аффинное определение средней точки M отрезка AB — это проективное гармоническое сопряжение бесконечно удаленной точки , P, прямой AB. То есть точка M такая, что H [A, B; ВЕЧЕРА]. Когда координаты могут быть введены в аффинную геометрию, два определения средней точки будут совпадать.

Средняя точка не определяется естественным образом в проективной геометрии, поскольку нет выделенной точки, которая могла бы играть роль точка на бесконечности (любая точка в проективном диапазоне может быть проективно отображена на любую другую точку в (том же или каком-либо другом) проективном диапазоне). Однако фиксация бесконечно удаленной точки определяет аффинную структуру на рассматриваемой проективной прямой , и приведенное выше определение может быть применено.

Определение средней точки сегмента может быть расширено до геодезических дуг на римановом многообразии. Обратите внимание, что, в отличие от аффинного случая, середина между двумя точками не может быть определена однозначно.

См. Также

Ссылки

Внешние ссылки

• Анимация — отображение характеристик средней точки отрезка
• Что такое формула средней точки

From Wikipedia, the free encyclopedia

In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.

Formula[edit]

The midpoint of a segment in n-dimensional space whose endpoints are and is given by

That is, the i^th coordinate of the midpoint (i = 1, 2, …, n) is

Construction[edit]

Given two points of interest, finding the midpoint of the line segment they determine can be accomplished by a compass and straightedge construction. The midpoint of a line segment, embedded in a plane, can be located by first constructing a lens using circular arcs of equal (and large enough) radii centered at the two endpoints, then connecting the cusps of the lens (the two points where the arcs intersect). The point where the line connecting the cusps intersects the segment is then the midpoint of the segment. It is more challenging to locate the midpoint using only a compass, but it is still possible according to the Mohr-Mascheroni theorem.^[1]

Geometric properties involving midpoints[edit]

Circle[edit]

The midpoint of any diameter of a circle is the center of the circle.

Any line perpendicular to any chord of a circle and passing through its midpoint also passes through the circle’s center.

The butterfly theorem states that, if M is the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn, then AD and BC intersect chord PQ at X and Y respectively, such that M is the midpoint of XY.

Ellipse[edit]

The midpoint of any segment which is an area bisector or perimeter bisector of an ellipse is the ellipse’s center.

The ellipse’s center is also the midpoint of a segment connecting the two foci of the ellipse.

Hyperbola[edit]

The midpoint of a segment connecting a hyperbola’s vertices is the center of the hyperbola.

Triangle[edit]

The perpendicular bisector of a side of a triangle is the line that is perpendicular to that side and passes through its midpoint. The three perpendicular bisectors of a triangle’s three sides intersect at the circumcenter (the center of the circle through the three vertices).

The median of a triangle’s side passes through both the side’s midpoint and the triangle’s opposite vertex. The three medians of a triangle intersect at the triangle’s centroid (the point on which the triangle would balance if it were made of a thin sheet of uniform-density metal).

The nine-point center of a triangle lies at the midpoint between the circumcenter and the orthocenter. These points are all on the Euler line.

A midsegment (or midline) of a triangle is a line segment that joins the midpoints of two sides of the triangle. It is parallel to the third side and has a length equal to one half of that third side.

The medial triangle of a given triangle has vertices at the midpoints of the given triangle’s sides, therefore its sides are the three midsegments of the given triangle. It shares the same centroid and medians with the given triangle. The perimeter of the medial triangle equals the semiperimeter (half the perimeter) of the original triangle, and its area is one quarter of the area of the original triangle. The orthocenter (intersection of the altitudes) of the medial triangle coincides with the circumcenter (center of the circle through the vertices) of the original triangle.

Every triangle has an inscribed ellipse, called its Steiner inellipse, that is internally tangent to the triangle at the midpoints of all its sides. This ellipse is centered at the triangle’s centroid, and it has the largest area of any ellipse inscribed in the triangle.

In a right triangle, the circumcenter is the midpoint of the hypotenuse.

In an isosceles triangle, the median, altitude, and perpendicular bisector from the base side and the angle bisector of the apex coincide with the Euler line and the axis of symmetry, and these coinciding lines go through the midpoint of the base side.

Quadrilateral[edit]

The two bimedians of a convex quadrilateral are the line segments that connect the midpoints of opposite sides, hence each bisecting two sides. The two bimedians and the line segment joining the midpoints of the diagonals are concurrent at (all intersect at)a point called the «vertex centroid», which is the midpoint of all three of these segments.^[2]: p.125

The four «maltitudes» of a convex quadrilateral are the perpendiculars to a side through the midpoint of the opposite side, hence bisecting the latter side. If the quadrilateral is cyclic (inscribed in a circle), these maltitudes all meet at a common point called the «anticenter».

Brahmagupta’s theorem states that if a cyclic quadrilateral is orthodiagonal (that is, has perpendicular diagonals), then the perpendicular to a side from the point of intersection of the diagonals always goes through the midpoint of the opposite side.

Varignon’s theorem states that the midpoints of the sides of an arbitrary quadrilateral form the vertices of a parallelogram, and if the quadrilateral is not self-intersecting then the area of the parallelogram is half the area of the quadrilateral.

The Newton line is the line that connects the midpoints of the two diagonals in a convex quadrilateral that is not a parallelogram. The line segments connecting the midpoints of opposite sides of a convex quadrilateral intersect in a point that lies on the Newton line.

General polygons[edit]

A regular polygon has an inscribed circle which is tangent to each side of the polygon at its midpoint.

In a regular polygon with an even number of sides, the midpoint of a diagonal between opposite vertices is the polygon’s center.

The midpoint-stretching polygon of a cyclic polygon P (a polygon whose vertices all fall on the same circle) is another cyclic polygon inscribed in the same circle, the polygon whose vertices are the midpoints of the circular arcs between the vertices of P.^[3] Iterating the midpoint-stretching operation on an arbitrary initial polygon results in a sequence of polygons whose shapes converge to that of a regular polygon.^[3][4]

Generalizations[edit]

The abovementioned formulas for the midpoint of a segment implicitly use the lengths of segments. However, in the generalization to affine geometry, where segment lengths are not defined,^[5] the midpoint can still be defined since it is an affine invariant. The synthetic affine definition of the midpoint M of a segment AB is the projective harmonic conjugate of the point at infinity, P, of the line AB. That is, the point M such that H[A,B; P,M].^[6] When coordinates can be introduced in an affine geometry, the two definitions of midpoint will coincide.^[7]

The midpoint is not naturally defined in projective geometry since there is no distinguished point to play the role of the point at infinity (any point in a projective range may be projectively mapped to any other point in (the same or some other) projective range). However, fixing a point at infinity defines an affine structure on the projective line in question and the above definition can be applied.

The definition of the midpoint of a segment may be extended to geodesic arcs on a Riemannian manifold. Note that, unlike in the affine case, the midpoint between two points may not be uniquely determined.

See also[edit]

• Center (geometry) § Projective conics
• Midpoint polygon
• Bisection § Line segment bisector
• Numerical integration § Quadrature rules based on interpolating functions

References[edit]

External links[edit]

• Animation – showing the characteristics of the midpoint of a line segment

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

• KL – средняя линия треугольника ABC
• K – середина стороны AB: AK = KB
• L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

• KL параллельна AC
• KL = ¹/₂ ⋅ AC

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

• △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
• Стороны △KBL в два раза меньше соответствующих сторон △ABC:
  AB = 2KB, BC = 2BL, AC = 2KL.
• S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

• KL || AC, KL = ¹/₂ ⋅ AC
• KM || BC, KM = ¹/₂ ⋅ BC
• ML || AB, ML = ¹/₂ ⋅ AB

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.

S₁ = S₂ = S₃ = S₄

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Решение

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC² = AB² + AC² = 6² + 8² = 100.
BC = 10.

Таким образом, средняя линия LM = ¹/₂ ⋅ BC = ¹/₂ ⋅ 10 = 5.