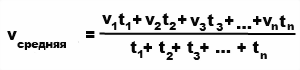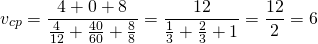Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути — со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
Калькулятор средней скорости
Рассчитайте онлайн среднюю скорость автомобиля или бегуна по времени и расстоянию.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
⏱️Что считает калькулятор
Калькулятор средней скорости — это инструмент, который используется для расчета онлайн средней скорости движения объекта. Он может быть полезен при планировании путешествий или спортивных мероприятий, где необходимо знать скорость, с которой вы перемещаетесь.
Калькулятор средней скорости может быть особенно полезен во время занятий спортом, таких как бег, плавание или велосипедная езда, где вы можете использовать его для измерения своих результатов и отслеживания своего прогресса. Также он может быть полезен для путешествий на автомобиле или на общественном транспорте, чтобы оценить, сколько времени вам понадобится, чтобы добраться до места назначения.
👨🏻💻 Как использовать калькулятор
Для использования калькулятора средней скорости необходимо ввести два параметра: расстояние, которое вы прошли, и время, за которое вы это сделали. Расстояние может быть измерено в километрах, милях, метрах или футах, а время — в часах, минутах или секундах. После того, как вы ввели эти значения, калькулятор автоматически вычисляет среднюю скорость в соответствующих единицах измерения.
Например, если вы прошли 10 километров за 2 часа, то средняя скорость будет 5 километров в час. Если вы предпочитаете мили в час, то калькулятор может перевести это значение в мили в час, в зависимости от вашего выбора единиц измерения.
🤓 Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора средней скорости зависит от нескольких факторов:
- Качество и точность входных данных. Если входные данные не точны, то и результаты расчетов не будут точными. Например, если вы неправильно измерили расстояние или время, то средняя скорость, которую вы рассчитаете, будет неточной.
- Единицы измерения. Необходимо использовать одни и те же единицы измерения для расстояния и времени. Если вы используете метры для измерения расстояния и часы для измерения времени, то вам нужно будет преобразовать эти единицы в одну систему измерения для точного расчета.
🏎️ Где можно применить калькулятор
Калькулятор средней скорости может быть использован в различных ситуациях, где необходимо определить, как быстро что-то двигалось или перемещалось. Некоторые примеры применения:
- Путешествия на автомобиле: можно использовать калькулятор, чтобы определить среднюю скорость вашей поездки, зная расстояние, которое вы проехали, и время, за которое вы это сделали.
- Спорт: калькулятор средней скорости может использоваться в различных видах спорта, таких как бег, плавание, езда на велосипеде и т.д., чтобы определить среднюю скорость, которую спортсмен достигает в течение определенного времени.
- Производство: калькулятор может использоваться для измерения скорости производственной линии или скорости конвейера, чтобы определить, насколько быстро проходит производственный процесс.
- Наука: калькулятор может использоваться в различных научных исследованиях, где необходимо измерить скорость перемещения различных объектов или процессов, например, в физике, химии или биологии.
- Логистика: калькулятор может использоваться для расчета средней скорости транспортных средств, которые используются в логистике, чтобы оценить время доставки товаров от одного места к другому.
🧮 Как вычислить среднюю скорость самостоятельно
Средняя скорость можно вычислить, разделив пройденное расстояние на затраченное время:
Средняя скорость = Пройденное расстояние / Затраченное время
Например, если вы прошли 5 километров за 1 час, то ваша средняя скорость будет:
Средняя скорость = 5 км / 1 ч = 5 км/ч
Обратите внимание, что средняя скорость может быть различной в разные моменты времени, особенно если скорость не является постоянной. В таких случаях нужно рассчитывать среднюю скорость на каждом участке и затем усреднять полученные значения.
🤔 Полезные советы
Несколько советов, которые могут помочь при расчете средней скорости:
- Измерьте расстояние: чтобы рассчитать среднюю скорость, вам нужно знать расстояние, которое вы прошли. Измерьте расстояние с помощью ленты или известной дистанции.
- Запишите время: чтобы рассчитать среднюю скорость, вам также нужно знать, сколько времени вы затратили на прохождение этого расстояния. Используйте секундомер или часы для измерения времени.
- Используйте правильную формулу: средняя скорость вычисляется как отношение расстояния к времени. Используйте правильную формулу для вашей ситуации. Например, для расчета средней скорости автомобиля используйте формулу V = D / T, где V — скорость, D — расстояние, T — время.
- Убедитесь, что единицы измерения соответствуют: при расчете средней скорости убедитесь, что единицы измерения расстояния и времени соответствуют друг другу. Например, если расстояние измерено в метрах, а время — в секундах, скорость должна быть выражена в метрах в секунду.
- Учитывайте направление движения: если вы двигались в разных направлениях со скоростью V1 и V2, то средняя скорость будет не V1 + V2, а (V1 + V2) / 2.
- Учитывайте остановки и паузы: если вы делали остановки или паузы на своем пути, учитывайте их при расчете средней скорости. Вычтите время, проведенное в паузах, из общего времени.
- Обратите внимание на изменение скорости: если вы двигались с разной скоростью на разных участках пути, учитывайте это при расчете средней скорости. Вычислите скорость на каждом участке пути, а затем найдите среднее значение.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы про вычисление средней скорости.
Что такое средняя скорость и как ее рассчитать?
Средняя скорость — это отношение пройденного расстояния к затраченному времени. Для ее расчёта нужно знать начальное и конечное положение объекта и время, за которое он пройдет расстояние между ними. Формула для расчета средней скорости: v = (s2 — s1) / t, где v — средняя скорость, s1 и s2 — начальное и конечное положение соответственно, t — время.
Какая единица измерения используется для средней скорости?
Единицей измерения средней скорости является метры в секунду (м/с) или километры в час (км/ч), в зависимости от предпочтений и системы единиц, используемой в конкретной области.
Можно ли рассчитать среднюю скорость без знания точных начального и конечного положения?
Нет, для расчета средней скорости необходимо знать начальное и конечное положение объекта. Если эта информация отсутствует, то среднюю скорость нельзя рассчитать.
Как связаны средняя скорость и средний темп?
Средняя скорость и средний темп связаны друг с другом, так как оба показателя относятся к скорости движения. Средний темп измеряется в минутах на километр, а средняя скорость — в метрах в секунду или километрах в час. Для перевода из одной единицы измерения в другую необходимо провести соответствующие математические операции.
Можно ли сравнивать средние скорости разных объектов?
Да, средние скорости разных объектов можно сравнивать, поскольку они выражаются в одной и той же единице измерения — метрах в секунду или километрах в час. Однако, необходимо учитывать различия в условиях движения, таких как погода, поверхность дороги, наличие препятствий и т.д., которые могут влиять на скорость движения объектов.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор закона Ома. Рассчитайте сопротивление, силу тока и напряжение в зависимости от известных параметров.
- Калькулятор коэффициента трения. Рассчитайте коэффициент трения по углу наклона или через массу силу трения.
- Калькулятор мощности тока. Рассчитайте онлайн мощность электрического тока в ваттах (Вт) в зависимости от силы тока, напряжения и сопротивления.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор перевода в тонны. Иногда может потребовать перевести одну единицу веса в другую, например, в тонны. И для этой цели очень пригодится специальный калькулятор.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии

Скорость транспорта — это показатель скорости в момент езды на нём. Нет определённых границ, с которой может двигаться транспорт или велосипед в частности. Скорость велосипеда зависит от многих факторов и условий. Например:
- От велосипедиста и его параметров — роста, веса, его физической подготовки.
- От погодных условий — скорости ветра, дорожного покрытия.
- Ну, и, конечно же, от самого велосипеда, его веса, параметров и т.д.
Средняя скорость велосипеда
Чтобы вычислить среднюю скорость езды на велосипеде, необходимо вычислить расстояние, которое проехал велосипедист за определённое время. Полученный результат может быть взят за основу, но он также может изменяться на другой местности или покрытии, и при других погодных условиях. Поэтому точную среднюю скорость можно высчитать только лишь условно и в каждом конкретном случае.
В наличии по лучшей цене велосипеды cube с доставкой до вашего региона!
На сегодняшний день самая высокая средняя скорость велосипедиста была зафиксирована в 2015 году. Британец Брэдли Уиггинс проехал 54 км 526 м за 1 час на крытом велодроме со специальным неизменным покрытием и рельефом, а также без влияния на скорость погодных условий. Обычные велосипедисты в городской черте ездят в среднем со скоростью до 20 км/час, а шоссейники способны поддерживать скорость около 30-35 км/час.
Максимальная скорость велосипеда
Людям всегда хочется бить прежние рекорды. Поэтому рекорды максимальной скорости на велосипеде постоянно меняются и увеличиваются. Причём, для этих целей используются различные, и даже нестандартные методы. Например, побить рекорд максимальной велосипедной скорости пытались в аэродинамичной капсуле. Итог — 133 км 28 м/ в час. Но и это не передел! При езде велосипедиста с горы максимальная скорость достигла 222 км в час! Не повторяйте! Опасно для жизни! А когда велосипеду добавили реактивный двигатель, то он ещё бы немного и взлетел бы в космос, а так достиг скорость 333 км в час!
В наличии детские велосипеды с доставкой до вашего региона! Большой выбор. Гарантия лучшей цены.
Какая скорость у вас может быть средней и максимальной — будет во многом зависеть от вышеуказанных параметров. Но, как говорит народная мудрость — тише едешь, дальше будешь! Не стоит обгонять ветер, если вы не принимаете участие в соревнованиях, берегите себя и своего железного коня!
Как находить среднюю скорость
Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.
Чтобы найти среднюю скорость, надо:
1) найти весь пройденный путь;
2) найти все время движения;
3) весь пройденный путь разделить на все время движения:
На примерах посмотрим, как находить среднюю скорость.
1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.
Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.
Находим все время движения: 2+3=5 часов.
Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.
2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.
Переведем минуты в часы: 30 минут = 0,5 часа.
Найдем весь пройденный автомобилем путь:
2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.
Находим все время движения:
Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:
3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.
Найдем весь путь велосипедиста:
3∙12 + 1∙0 + 2∙9 = 54 км.
Найдем все время движения:
Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:
самый лучший сайт по математике спасибо огромное
Илья, спасибо за теплые слова!
Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно
Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.
Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?
Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.
Источник
Как решать задачи на среднюю скорость
В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:
Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!
Средняя скорость объекта
Для начала вспомним формулу, по которой решаются все задачи на движение: ( S=vt ) — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:
Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком. Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной. Поэтому, если в задаче дано несколько промежутков, то мы должны найти общий путь, который равен сумме всех промежутков вашего пути (то есть ( S=S_1+S_2+ldots+S_n ) (где ( n ) — количество путей, на которых скорость была постоянной). Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть ( t=t_1+t_2+ldots+t_n ) , причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: ( t_n=dfrac )
Решение задач
А теперь, обогатившись некоторой теорией решим первую из предложенных задач:
Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
Решение:
Теперь мы знаем длину всего пути ( ( 3S ) ) и сколько времени автомобиль затратил на прохождение всего пути ( ( t=dfrac<9s> <48>) , значит найти среднюю скорость не составит и труда:
Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок
Ответы к текстовым задачам:
Видео-урок: “Как решать задачу на нахождение средней скорости”:
В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.
Источник
Текстовые задачи на среднюю скорость.
Чтобы найти среднюю скорость движения, необходимо все расстояние разделить на все время движения.
Задача 1. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Найдём время движения автомобиля:
1. 105:35=3(ч) — время, за которое автомобиль проехал 105 км со скоростью 35 км/ч.
2. 120:60=2(ч) — время, за которое автомобиль проехал 120 км со скоростью 60 км/ч.
3. 500:100=5(ч) — время, за которое автомобиль проехал 500 км со скоростью 100 км/ч.
4. 3+2+5=10(ч) — время движения автомобиля.
Найдём расстояние, которое проехал автомобиль:
Найдём среднюю скорость автомобиля:
Ответ: средняя скорость автомобиля равна 72,5 км/ч.
Задача 2. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую – со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Пусть автомобиль проехал Х км.
Найдём время движения автомобиля:
1. Х/110(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 55 км/ч.
2. Х/140(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 70 км/ч.
Найдем среднюю скорость:
Ответ: 61,6 км/ч.
Задачи для самостоятельного решения:
1. Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км – со скоростью 80 км/ч, а последние 140 км – со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
2. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км – со скоростью 60 км/ч, а последние 225 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
3. Первую половину трассы автомобиль проехал со скоростью 65 км/ч, а вторую половину трассы со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Источник
Текстовые задачи на среднюю скорость.
Чтобы найти среднюю скорость движения, необходимо все расстояние разделить на все время движения.
Задача 1. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Найдём время движения автомобиля:
1. 105:35=3(ч) — время, за которое автомобиль проехал 105 км со скоростью 35 км/ч.
2. 120:60=2(ч) — время, за которое автомобиль проехал 120 км со скоростью 60 км/ч.
3. 500:100=5(ч) — время, за которое автомобиль проехал 500 км со скоростью 100 км/ч.
4. 3+2+5=10(ч) — время движения автомобиля.
Найдём расстояние, которое проехал автомобиль:
Найдём среднюю скорость автомобиля:
Ответ: средняя скорость автомобиля равна 72,5 км/ч.
Задача 2. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую – со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Пусть автомобиль проехал Х км.
Найдём время движения автомобиля:
1. Х/110(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 55 км/ч.
2. Х/140(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 70 км/ч.
Найдем среднюю скорость:
Ответ: 61,6 км/ч.
Задачи для самостоятельного решения:
1. Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км – со скоростью 80 км/ч, а последние 140 км – со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
2. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км – со скоростью 60 км/ч, а последние 225 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
3. Первую половину трассы автомобиль проехал со скоростью 65 км/ч, а вторую половину трассы со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Источник
Средняя скорость пути
Известно, что средняя скорость V равна пути S, деленному на время t средней скорости. Средняя скорость не всегда находится так легко. В случае, если автомобиль движется равномерно с постоянной скоростью, например 45 км/час, то, очевидно, средняя скорость и постоянная скорость одинаковы, т. е. 45 км/час. Если же автомобиль трогается с места (начальная скорость равна 0) и развивает скорость постепенно, то среднюю скорость можно найти следующим способом: нужно записать сумму всех скоростей и поделить ее на число отсчетов скоростей. Важно — временные интервалы должны быть одинаковые (например: записывать скорость каждые 5 секунд, или каждые 7 минут).
Калькулятор средней скорости пути
Складывая скорости, введенные вами, мы находим их сумму. Разделив эту сумму на количество равных временных отсчетов, мы узнаем среднюю скорость.
Единицы скорости
Скорость обычно определяют как путь, пройденный за единицу времени. Поэтому, если скорость автомобиля 90 км/час, то он за минуту должен пройти 1,5 км, а в секунду 1500 : 60, или 25 м. Следовательно, скорость 90 км/час может быть выражена различными способами в зависимости от выбора единиц времени и пути:
90 км/час = 1.5 км/мин =25 м/сек.
Поскольку скорость может быть выражена в различных единицах, то надо внимательно следить за выбором единиц в формуле S=vt. Если скорость выбираем в км/час, то время надо брать в часах, если — в м/сек, то время должно быть выражено в секундах.
Источник
Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.
Чтобы найти среднюю скорость, надо:
1) найти весь пройденный путь;
2) найти все время движения;
3) весь пройденный путь разделить на все время движения:
На примерах посмотрим, как находить среднюю скорость.
1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.
Решение:
Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.
Находим все время движения: 2+3=5 часов.
Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.
2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.
Решение:
Переведем минуты в часы: 30 минут = 0,5 часа.
Найдем весь пройденный автомобилем путь:
2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.
Находим все время движения:
2 + 1,5 + 0,5 = 4 часа.
Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:
273:4 = 68,25 км/ч.
3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.
Решение:
Найдем весь путь велосипедиста:
3∙12 + 1∙0 + 2∙9 = 54 км.
Найдем все время движения:
3 + 1 + 2 = 6 часов.
Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:
54:6=9 км/ч.