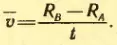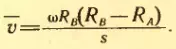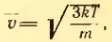Как найти среднюю скорость теплового движения молекул - AvtoShod.ru

Средняя скорость теплового движения молекул. Уравнение (2.9) дает возможность найти среднюю скорость теплового движения молекул. Подставляя в это уравнение 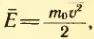получим выражение для среднего квадрата скорости:

(2.11)

Отсюда средняя скорость молекулы (точнее, средняя квадратическая скорость) равна:

(2.12)

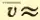
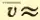
Вычисляя по формуле (2.12) скорость молекул, например азота, при t = 0°C, получим: 500 м/с. Молекулы водорода при той же температуре имеют скорость 1800 м/с.
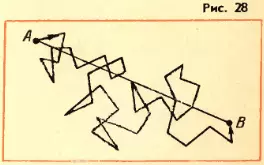
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчетам оказались большими, чем скорости артиллерийских снарядов! Высказывали на этом основании даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла. Это нетрудно объяснить. Из-за столкновений молекул траектория каждой молекулы представляет собой запутанную ломаную линию (рис. 28). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком либо направлении в среднем невелико даже за время нарядна нескольких минут. При перемещении молекулы из точки A в точку B пройденный ею путь оказывается гораздо больше расстояния |AB|.

Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (2.12). Один из опытов был предложен Штерном в 1920 г.

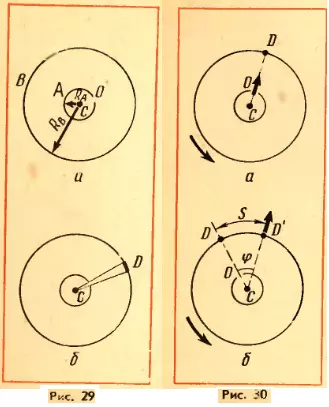
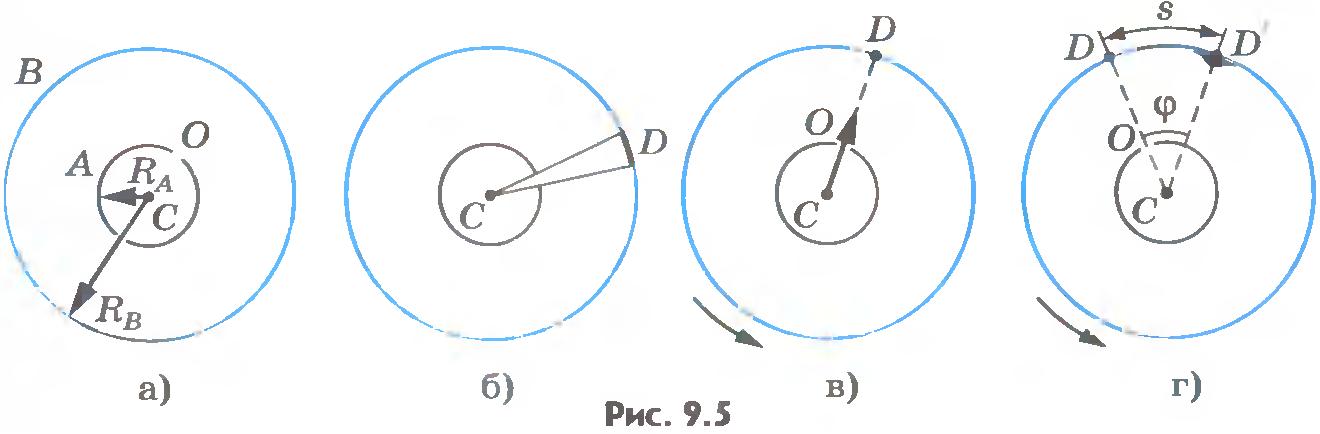
Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жестко связанных друг с другом (рис. 29, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка C, покрытая слоем серебра. По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель O. Воздух из цилиндров откачан. Цилиндр B находится при комнатной температуре.

Затем цилиндры приводит во вращение с угловой скоростью ω. Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров R_B — R_A, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадут на внутреннюю поверхность большого цилиндра не прямо против щели O (рис. 30, а), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 30, б). Ведь атомы движутся прямолинейно. Расстояние s равно:

s = φ R_B = ωtR_B (2.13)

В действительности не все атомы серебра имеют одну и ту же скорость. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полоскал D и D’ с наибольшей концентрацией атомов серебра. Этому расстоянию будет соответствовать средняя скорость атомов.

Средняя скорость атома равна:

Подставляя в эту формулу значение t из выражения (2.13), получим:

Зная ω, R_A и R_B и измеряя среднее смещение s полоски серебра, вызванное вращением прибора, находим среднюю скорость атомов серебра.

Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратической скорости. Это служит экспериментальным доказательством справедливости формулы (2.12), а следовательно и (2.9), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.

Средняя скорость броуновской частицы. Формула (2.12) позволяет понять почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица, участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (2.9), а средняя квадратическая скорость — формулой

где m — масса броуновской частицы. Если масса частицы велике, то средняя скорость ее движения настолько мала, что движение частицы практически нельзя обнаружить.

1. Как изменится средняя квадратическая скорость движения молекул при увеличении температуры в 4 раза? 2. Какие молекулы в атмосфере движутся быстрее: молекулы азота или молекулы кислорода? 3. Почему толщина слоя полоски серебра на поверхности внешнего вращающегося цилиндра в опыте Штерна неодинакова по ширине полоски?

Источник

Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.

Виды скоростей молекул газа

Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.

Средняя (или среднеарифметическая) скорость определяется уравнением

v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}

где viv_i – скорость ii-й молекулы;

nn –количество молекул.

Средняя квадратичная скорость определяется как:

vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}

По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.

Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,

vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}

Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.

Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.

Экспериментальное определение скоростей газовых молекул

Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.

Примечание

В других опытах использовали также висмут, кадмий, цезий.

Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10^-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s₁ и s₂ проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.

Рис. 1

На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а₁. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с^-1.

При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,

t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}

где vv – скорость атомов серебра.

Отсюда

v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}

Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением

(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}

что согласуется со средней скоростью молекул, которые определяются по формуле

v=8kTπmv=sqrt{frac{8kT}{pi m}}

Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.

Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).

Рис. 2

Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.

Тест по теме «Скорость движения молекул»

Источник

Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.

Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см³ при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.

Что такое средняя скорость движения молекул

Среднюю скорость движения молекул часто именуют скоростью их теплового движения.

Определение 1

Вид формулы средней относительной скорости молекул в физике можно представить выражением:

[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]

Выражение под корнем – средняя скорость молекул идеального газа.

Как определить среднюю квадратичную скорость движения молекул

Определение 2

Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.

Средняя скорость молекул равна:

[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]

Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:

[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]

Ещё одно выражение для среднеквадратичной скорости:

[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории

P = (1/3)nm*<Vкв>

Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.

Пример. 1.

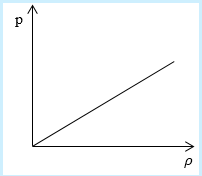
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:

Где P — давление, ρ — плотность

Напомним, что средняя скорость частиц:

[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]

Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ‎. Эти две величины можно связать соотношением

P=C*ρ‎

Где С – некоторая постоянная величина, константа.

Далее считаем m₀= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.

Нужно лишь подставить эти значения в формулу для средней скорости:

[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]

В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.

Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.

Нет времени решать самому?

Наши эксперты помогут!

Пример. 2.

Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).

Воспользуемся формулой:

[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]

Также нам потребуется уравнение Менделеева-Клайперона

Здесь мы воспользовались тем, что:

m/μ = N/N_a

PV = (m/μ)*RT = (N/N_a)*RT

Если обе части этого уравнения поделить на V и принять во внимание, что

(N/V) = n, то можно получить

P = (n/N_a)*RT. Отсюда находим, что RT = (p*N)/n

Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:

[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]

Источник

Екатерина Владимировна Мосина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Различают следующие скорости, характеризующие движение молекул.

Средняя скорость движения молекул

средняя скорость движения молекул $leftlangle vrightrangle $, которая определяется как:

где N — число молекул. Или, среднюю скорость можно найти как:

где $Fleft(vright)=4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2$ — функция распределения молекул по модулю скорости, указывающая долю молекул со скоростями, находящимися в единичном интервале $dv$ около величины скорости $v$, $m_0$- масса молекулы, $k$- постоянная Болцмана, T — термодинамическая температура. Для того, чтобы определить, как средняя скорость молекулы связана с макропараметрами газа, как системы частиц, найдем значение интеграла (2).

Произведем замену:

Следовательно:

Подставим (4) и (5) в (3), получим:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Проведем интегрирование по частям, получим:

где R — универсальная газовая постоянная, $mu $- молярная масса газа.

Среднюю скорость движения молекул называют также скоростью теплового движения молекул.

Средняя относительная скорость молекул:

[leftlangle v_{otn}rightrangle =sqrt{2}sqrt{frac{8kT}{pi m_0}}=sqrt{2}leftlangle vrightrangle left(7right).]

Средняя квадратичная скорость

Средней квадратичной скоростью движения молекул газа называют величину:

[leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{{v_i}^2}}left(8right).]

Или

[{leftlangle v_{kv}rightrangle }^2=intnolimits^{infty }_0{v^2Fleft(vright)dv left(9right).}]

Проводя интегрирование, которое аналогично интегрированию при получении связи средней скорости с температурой газа, получим:

[leftlangle v_{kv}rightrangle =sqrt{frac{3kT}{m_0}}=sqrt{frac{3RT}{mu }}left(10right).]

Именно средняя квадратичная скорость поступательного движения молекул газа входит в основное уравнение молекулярно-кинетической теории:

[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(11right),]

где $n=frac{N}{V}$ — концентрация частиц вещества, $N$- число частиц вещества, V- объем.

«Средняя скорость молекул» 👇

Пример 1

Задание: Определите, как изменяется средняя скорость движения молекул идеального газа при увеличении давления в процессе, представленном на графике (рис.1).

Рис. 1

Решение:

Запишем выражение для средней скорости движения молекул газа в виде:

[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}} left(1.1right)]

По графику видим, что $psim rho или p=Crho , $ где C- некоторая константа.

[m_0=frac{rho }{n}, p=nkT=Crho to kT=frac{Crho }{n} left(1.2right).]

Подставим (1.2) в (1.1), получим:

[leftlangle vrightrangle =sqrt{frac{8kT}{pi m_0}}=sqrt{frac{8Crho }{pi n}frac{n}{rho }}=sqrt{frac{8C}{pi }}left(1.3right)]

Ответ: В процессе, изображенном на графике, с ростом давления средняя скорость движения молекул не изменяется.

Пример 2

Задание: Можно ли вычислить среднюю квадратичную скорость молекулы идеального газа, если известны: давление газа (p), молярная масса газа ($mu $) и концентрация молекул газа (n)?

Решение:

Используем выражение для $leftlangle v_{kv}rightrangle :$

[leftlangle v_{kv}rightrangle =sqrt{frac{3RT}{mu }}left(2.1right).]

Кроме того, из уравнения Менделеева — Клайперона и зная, что $frac{m}{mu }=frac{N}{N_A}$:

[pV=frac{m}{mu }RT=frac{N}{N_A}RTleft(2.2right).]

Разделим правую и левую части (2.2) на V, зная, что $frac{N}{V}=n$ получим:

[p=frac{n}{N_A}RTto RT=frac{pN_A}{n} left(2.3right).]

Подставим (2.3) в выражение для среднеквадратичной скорости (2.1), имеем:

[leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}} left(2.4right).]

Ответ: По заданным в условии задачи параметрам среднеквадратичную скорость движения молекул газа вычислить можно с помощью формулы $leftlangle v_{kv}rightrangle =sqrt{frac{3pN_A}{mu n}}.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Измерение скоростей молекул газа

Зная температуру, нетрудно вычислить среднюю кинетическую энергию молекул газа. После этого легко вычислить и среднюю скорость молекулы. А можно ли эту скорость измерить? Ведь молекулы так малы!
Средняя скорость теплового движения молекул. Уравнение (9.9) дает возможность найти средний квадрат скорости движения молекулы. Подставив в это уравнение получим выражение для среднего квадрата скорости:

Квадратный корень из этой величины называется средней квадратичной скоростью:

Вычисляя по формуле (9.12) скорость молекул, например азота при t=0°С, получим . Молекулы водорода при той же температуре имеют среднюю скорость .
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчетам оказались больше, чем скорости артиллерийских снарядов! На этом основании высказывали даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла. Это нетрудно объяснить. Из-за столкновения молекул траектория каждой молекулы представляет собой запутанную ломаную линию (рис.9.4). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком-либо направлении в среднем невелико даже за время порядка нескольких минут. Вот и получается, что при перемещении молекулы из точки A в точку B пройденный ею путь оказывается гораздо больше расстояния AB.

Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (9.12). Один из опытов был предложен и осуществлен О. Штерном в 1920 г.
Прибор Штерна состоит из двух коаксиальных цилиндров A и B, жестко связанных друг с другом (рис.9.5, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка C, покрытая слоем серебра. По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель O. Воздух из цилиндров откачан. Цилиндр B находится при комнатной температуре.

   Вначале прибор неподвижен. При прохождении тока по нити слой серебра испаряется и внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель O и, достигнув внутренней поверхности цилиндра B, осаждаются на ней. В результате прямо против щели образуется узкая полоска D серебра (рис.9.5, б).
   Затем цилиндры приводят во вращение с большим числом оборотов n в секунду (до 1500 1/c). Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров R_B-R_A, цилиндры повернутся на некоторый угол . В результате атомы, движущиеся с постоянной скоростью, попадают на внутреннюю поверхность большого цилиндра не прямо против щели O (рис.9.5, в), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис.9.5, г): ведь атомы движутся прямолинейно.
   Если через обозначить модуль скорости вращения точек поверхности внешнего цилиндра, то

В действительности не все атомы серебра имеют одну и ту же скорость. Поэтому расстояния s для различных атомов будут несколько отличаться. Под s следует понимать расстояние между участками на полосках с наибольшей концентрацией атомов серебра. Этому расстоянию будет соответствовать средняя скорость атомов, которая равна:

Подставляя в эту формулу значение времени t из выражения (9.13), получим

   Зная n, R_A и R_B и измеряя среднее смещение полоски серебра, вызванное вращением прибора, можно найти среднюю скорость атомов серебра.
   Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратичной скорости. Это служит экспериментальным доказательством справедливости формулы (9.12), а следовательно, и формулы (9.9), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.
   Средние скорости молекул превышают скорость звука и достигают сотен метров в секунду. Эти скорости удалось измерить благодаря тому, что макроскопическим телам (цилиндрам в опытах Штерна) можно сообщить столь большую скорость, что за время пролета молекул между цилиндрами они поворачиваются на заметный угол.

   ???
   1. Почему толщина слоя полоски серебра на поверхности внешнего вращающегося цилиндра в опыте Штерна неодинакова по ширине полоски?
   2. Как изменится средняя квадратичная скорость движения молекул при увеличении температуры в 4 раза?
   3. Какие молекулы в атмосфере движутся быстрее: молекулы азота или молекулы кислорода?

Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс

_{Сборник конспектов уроков по всем классам, домашнее задание, скачать рефераты по физике, книги и учебники согласно календарного планирования по физике для 10 класса}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: