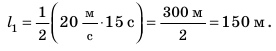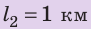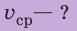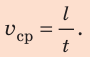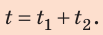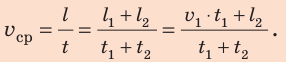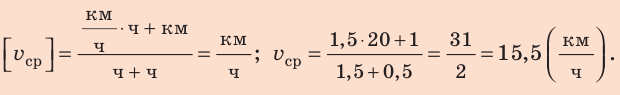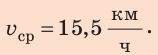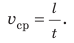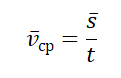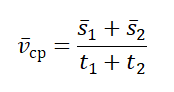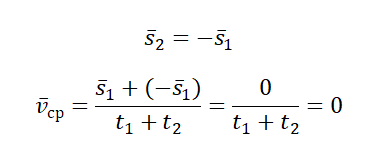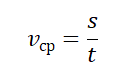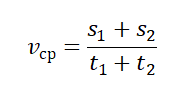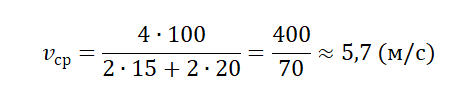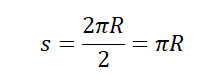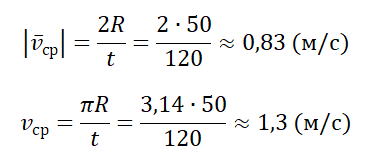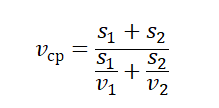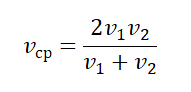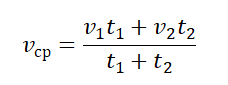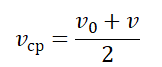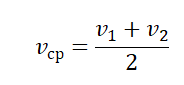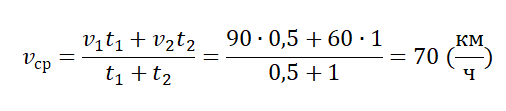Как определяют среднюю скорость при неравномерном движении?
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §16. Вопросы. Номер №5
Решение
Чтобы определить среднюю скорость тела (
v
с
р
) при неравномерном движении надо весь пройденный путь разделить на всё время движения:
v
с
р
=
S
t
.
При неравномерном движении тела средняя скорость характеризует движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в различные моменты времени этого промежутка.
Содержание:
Неравномерное движение:
Наверняка вам случалось ехать на автобусе или автомобиле из одного города в другой. Вспомните: транспортное средство время от времени тормозит, останавливается, потом снова набирает скорость… Стрелка спидометра все время колеблется и только иногда замирает на месте. Можно ли назвать такое движение равномерным? Конечно, нет. А как называют такое движение? Как его описывают?
В повседневной жизни мы обычно имеем дело с неравномерным движением. Так, неравномерным является движение автобуса (рис. 11.1) и других транспортных средств, движение падающих тел, движение спортсменов на беговой дорожке. А еще вспомните, например, как катится мяч, как вы движетесь во время прогулки, на уроках физкультуры и т. д.
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Обратите внимание! При неравномерном движении значение скорости движения тела со временем изменяется. Попробуйте привести примеры неравномерного движения. Теперь мы можем классифицировать виды механического движения (см. таблицу): по форме траектории — прямолинейное, криволинейное; по характеру движения тела — равномерное, неравномерное
Вычисляем среднюю скорость движения тела
Предположим, что поезд прошел 150 км (расстояние между двумя станциями) за 2,5 ч. Если разделить 150 км на 2,5 ч, получим скорость движения поезда — 60 км/ч. Но ведь поезд двигался неравномерно! В таком случае говорят, что получена средняя скорость движения поезда (рис. 11.2).
Средняя скорость движения тела 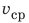
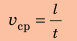
График скорости неравномерного движения тела
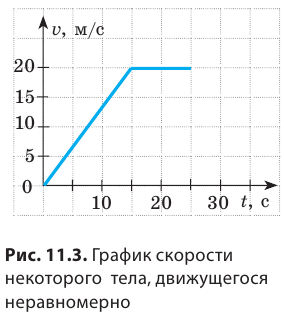
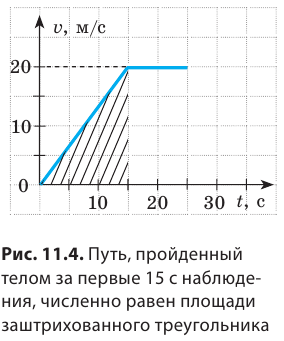
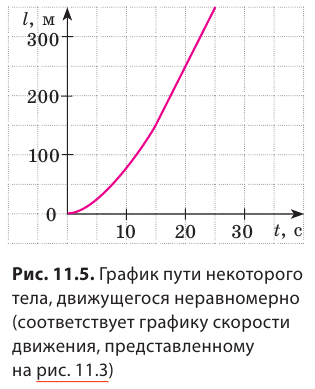
Рассмотрим график скорости неравномерного движения некоторого тела (рис. 11.3) и определим: как двигалось тело; какой путь прошло тело за 25 с наблюдения; какой была средняя скорость движения тела на данном пути. По графику видим, что скорость движения тела в течение первых 15 с равномерно увеличивалась от 0 до 20 м/с. Чтобы вычислить путь, пройденный телом за это время, вспомним: числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела. Итак, определим площадь заштрихованного треугольника (рис. 11.4). Из рисунка видим, что площадь заштрихованного треугольника равна половине площади прямоугольника с «длиной» 20 м/с и «шириной» 15 с. Площадь прямоугольника, в свою очередь, равна произведению его длины и ширины. Таким образом, путь 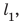
Следующий интервал времени 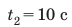
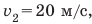
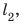
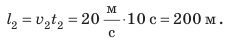
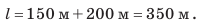
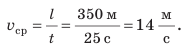
Обратите внимание! Путь не может уменьшаться, поэтому график пути либо поднимается, либо остается горизонтальным, но никогда не опускается.
- Заказать решение задач по физике
Пример
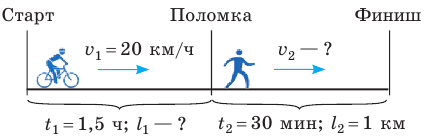
Полтора часа мальчик ехал на велосипеде со скоростью 20 км/ч. Потом велосипед сломался, и последний километр пути мальчик шел пешком. Какой была средняя скорость движения мальчика на всем пути, если пешком он шел полчаса? Анализ физической проблемы. Выполним пояснительный рисунок. Для определения средней скорости движения нужно найти путь, который преодолел мальчик, и время его движения. Время движения выражено в часах, путь — в километрах, поэтому среднюю скорость движения найдем в километрах в час.
Дано:
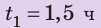
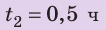
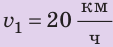
Найти:
Решение:
По определению:
Путь l, который преодолел мальчик, равен: 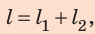
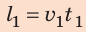
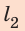
Подставив выражения для l и t в формулу средней скорости движения, получим:
Проверим единицу, найдем значение искомой величины:
Анализ результатов. Мальчик ехал на велосипеде со скоростью 20 км/ч, шел пешком со скоростью 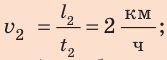
Ответ:
Итоги:
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Виды механического движения: по форме траектории — прямолинейное и криволинейное; по зависимости скорости движения от времени — равномерное и неравномерное. Средняя скорость движения тела равна отношению всего пути, пройденного телом, к интервалу времени, за который этот путь пройден:
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Относительность движения
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*}
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | — | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | — | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | — | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) — скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | — | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) — время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Определение и формулы
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
vср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Определение и формулы
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср=vср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>vср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Полезные советы и формулы
- Если известны значения отдельных участков пути и скорости на этих участках, средняя скорость равна:
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Алиса Никитина | Просмотров: 5.7k
Неравномерное движение.
Средняя скорость
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
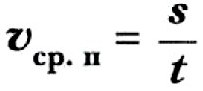
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения , совершённого телом, к длительности этого промежутка времени.
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Ответ: 70 км/ч
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Масса тела. Плотность вещества
- Вернуться к списку конспектов по Физике
- Посмотреть решение типовых задач на движение