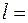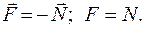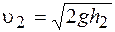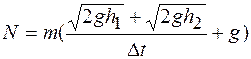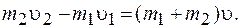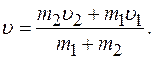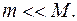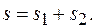ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Условие задачи:
Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30° к ней и отскакивает без потери скорости. Найти среднюю силу, действующую на мяч со стороны стенки, если скорость мяча 10 м/с, а продолжительность удара 0,1 с.
Задача №2.1.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=0,15) кг, (alpha=30^circ), (upsilon=10) м/с, (Delta t=0,1) с, (F-?)
Решение задачи:
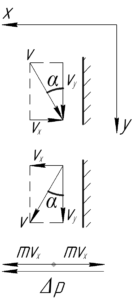
[F = frac{{Delta p}}{{Delta t}};;;;(1)]
В этой формуле (Delta p) – это изменение импульса мяча вследствие удара о стенку, (Delta t) – известное из условия время взаимодействия.
Найдем изменение импульса мяча. На рисунке изображены моменты непосредственно перед ударом и сразу после удара. Так как потерь скорости нет, то удар считается абсолютно упругим, поэтому мяч отскочит под тем же углом. Проецируем скорость мяча перед ударом и после удара на оси (x) и (y).
Видно, что по оси (y) проекции скорости (upsilon_y) равны до и после удара (upsilon cos alpha), поэтому изменения импульса мяча в этом направлении не было, а значит, в этом направлении и не действует сила.
По оси (x) модуль изменения импульса составит (смотри нижнюю часть схемы):
[Delta p = 2m{upsilon _x} = 2mupsilon sin alpha ;;;;(2)]
Подставим (2) в (1), получим решение задачи в общем виде.
[F = frac{{2mupsilon sin alpha }}{{Delta t}}]
Подставляем данные задачи в эту формулу, считаем численный ответ.
[F = frac{{2 cdot 0,15 cdot 10 cdot sin 30^circ }}{{0,1}} = 15; Н]
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
Чтобы узнать искомую среднюю силу удара, рассмотрим равенство: Fср * t = mм * V, откуда выражаем: Fср = mм * V / t.
Данные: mм — масса мяча (mм = 0,6 кг); V — полученная мячом скорость (V = 12 м/с); t — длительность рассматриваемого удара (t = 0,04 с).
Выполним расчет: Fср = mм * V / t = 0,6 * 12 / 0,04 = 180 Н.
Ответ: Средняя сила удара, согласно расчету, составляет 180 Н.
Закон сохранения импульса выполняется для любого удара.
Вопросы для ответа у доски:
1. Абсолютно неупругий удар.
Получите выражение для скорости двух не упруго столкнувшихся шаров. Найдите работу внутренних неконсервативных сил при деформации шаров и кинетическую энергию шаров после их соударения. Расскажите о практическом применении неупругого удара.
2. Абсолютно упругий удар.
Рассмотрите центральный удар двух упругих шаров и получите выражение скорости в векторной форме. Примените полученные формулы к различным частным случаям соударения двух шаров и шара с упругой стенкой.
Примеры решения задач:
Задача 1. Мяч массой 50гсвободно падает без начальной скорости с высоты 2м на пол и подскакивает на высоту 1м. Определить среднюю силу удара мяча о пол. Продолжительность удара 0,02с.
Поскольку высота подъёма мяча после удара изменилась, то это не абсолютно упругое соударение ( 
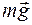


По III закону Ньютона силы 

Найдём 




Тогда,

где 



Спроецируем уравнение на ось Y:

Отсюда:






Тогда,
Вычислим:

В задаче необходимо определить среднююсилу удара мяча о пол. Во II законе Ньютона под 

Так как в данной задаче сила удара 

Итак,

Ответ: 
Задача 2. Снаряд массой 50кг, летящий параллельно рельсам со скоростью 400м/с, попадает в движущуюся платформу с песком массой 20т и застревает в песке. С какой скоростью будет двигаться платформа со снарядом, если:
1) она катилась навстречу снаряду со скоростью 2м/с;
2) она катилась в сторону движения снаряда со скоростью 2м/с;
3) она покоилась?
ствует сила 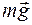
В задаче можно выделить 2 состояния системы: до и после попадания снаряда в песок. На Рис.2.5.2 показаны импульсы тел системы в указанных состояниях.

Взаимодействие тел – неупругое, так как после попадания снаряда в песок, система тел будет двигаться с общей скоростью 
Запишем закон сохранения импульса в проекции на ось Х:
Выразим из полученного уравнения скорость 

Подставляя в выражение для u заданные числовые значения, получим:

2) Случай 2:
В данном случае закон сохранения импульса в проекции на ось Х будет выглядеть так:
Вычисляя, получим: 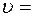
3) Случай 3:



Ответ: 1) 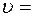
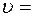
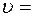
Задача 3. Баба копра масой 500 кг падает на сваю массой 120 кг со скоростью 4 м/с. Определить КПД удара бабы копра о сваю. Удар неупругий.
| Дано: | Решение: |
 500 кг 500 кг
|
Систему, состоящую из бабы копра и сваи, считаем замкнутой во время удара, когда силы ударного взаимодействия значительно превышают равнодействующую сил тяжести и силы реакции опоры. К такой системе можно применить закон сохранения импульса. |
 120 кг 120 кг
|
|
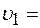 4 м/с 4 м/с
|
|
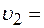 0 0
|
|
Найти: 
|
Решение:
Во время удара изменяется только кинетическая энергия тел, поэтому энергия 
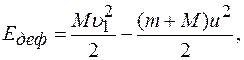
где 
Из закона сохранения импульса:

отсюда:
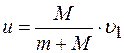
Подставив в (1) значение скорости 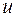

Полезная энергия – это энергия, затраченная на деформацию. КПД удара:

Подставив числовые значения в (4), получаем:

Ответ: 
Вопросы и задания для самопроверки:
1. Что называется ударом?
2. Дайте определение прямого, центрального и косого ударов.
3. Какой удар называется абсолютно упругим; абсолютно неупругим?
4. Опишите процесс абсолютно упругого соударения двух тел. На какие два этапа делится процесс соударения? Как изменяется кинетическая и потенциальная энергия тел в процессе соударения?
5. Опишите процесс неупругого соударения тел.
6. Какими законами сохранения можно пользоваться при рассмотрении упругого и неупругого ударов?
Задачи для самостоятельного решения:
1. На стоящий на горизонтальном полу клин массой 5кг с высоты 1,5м падает шар массой 1кг и отскакивает в горизонтальном направлении. Найти горизонтальную скорость клина после удара. Трением пренебречь, удар шара о клин считать абсолютно упругим.
2. Какова средняя сила давления на плечо при стрельбе из автомата, если масса пули равна 10г, а скорость пули при вылете из ствола равна 400м/с? Автомат делает 300 выстрелов в минуту.
3. Шар массой 3 кг движется со скоростью 4 м/с и ударяется о неподвижное тело такой же массы. Считая удар неупругим, найти количество теплоты, выделившейся при ударе.
4. Тело массой 


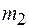
5. Тело массой 1кг начинает движение из состояния покоя под действием постоянной силы, равной 10 Н. Каков будет импульс тела 
6. Шайбе, находящейся на плоскости, образующей с горизонтом угол 
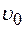

7. Мяч падает на пол с высоты 

8. На легких стержнях длиной 



9. Два шара массами 
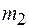
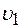
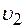
а) Определите скорости шаров после соударения. б) Исследуйте полученный результат в зависимости от соотношения между массами и скоростями шаров, найдите условие, при котором происходит наибольшая передача кинетической энергии. в) Найдите импульс и энергию каждого шара в системе отсчета, связанной с их центром масс, суммарную кинетическую энергию шаров.
10. Три небольших гладких шара A, B и C лежат на одной прямой на расстоянии 






11. Тело массой 
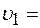

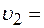


12. Тело массой 




13. Два тела движутся навстречу друг другу и соударяются неупруго. Скорости тел до удара были 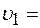
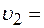

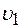


14. Два шара с массами 



15. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня 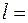


16. Стальной шарик массой 




17. Тело массы 

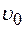
18. Какую мощность развивают двигатели ракеты массы 
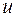
19. Тело массы 

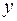


20. Тонкая цепочка массы 
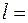



21. Потенциальная энергия частицы в некотором поле имеет вид: 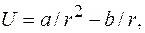
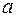


а) значение 
б) максимальное значение силы притяжения; изобразить примерные графики зависимостей 
22. 
23. Показать, что изменение кинетической энергии при неупругом ударе зависит только от относительной скорости тел до удара и от их масс.
24. Молот массой 1,5 

25. Два стальных шара подвешены на нитях так, что при их касании центры тяжести находятся на