Мощность, формула
Мощностью P называется отношение произвольной работы W к времени t, в течение которого совершается работа.
[
textit{Мощность} = frac{textit{Работа}}{textit{Время}}
]
Единица СИ мощности
[
[P] = text{Ватт} enspace text{(Вт)} = frac{text{Джоуль}}{text{секунда}} = text{кг} frac{м^2}{с^3}
]
Средняя мощность, формула
Если:
P — Средняя мощность (Ватт),
W — Работа (Джоуль),
t — Время затраченное на совершение работы (секунд),
то
[
average{P} = frac{W}{t}
]
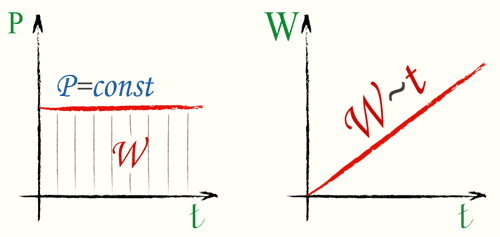
Вычислить, найти среднюю мощность по формуле (3)
Мгновенная мощность, формула
В большинстве случаев мощность зависит от времени, P=P(t).
Мгновенная мощность есть производная работы по времени:
[
P = frac{dW}{dt} = dot{W}
]
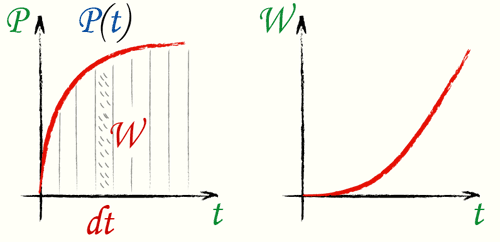
Поскольку см. (Работа)
[
dW = Fds
]
то отсюда следует см. (Мгновенная скорость)
[
P = F frac{ds}{dt} = Fu
]
Здесь:
F — Мгновенная сила (Ньютон),
u — мгновенная скорость (метр/секунда),
Мгновенная мощность равна произведению мгновенной силы на мгновенную скорость
При равномерно ускоренном движении F=const
[
P_{max} = F u_{max} ; average{P} = F average{u}
]
Вычислить, найти мгновенную мощность, по формуле (6)
Мощность |
стр. 471 |
|---|
Мощность
Различные машины и механизмы, выполняющие одинаковую работу, могут отличаться мощностью. Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.
При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.
Средняя мощность силы — скалярная физическая величина Ν, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается:
(~N = frac{A}{Delta t}.)
В СИ единицей мощности является ватт (Вт).
Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу (~A = F Delta r cos alpha). Поэтому мощность этой силы
(~N = frac{F Delta r cos alpha}{Delta t} = F upsilon cos alpha = F_{upsilon} cdot upsilon.)
где Fυ — проекция силы на направление движения.
По этой формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значения средней (~mathcal h upsilon mathcal i) или мгновенной υ скорости.
Мгновенная мощность — это мощность силы в данный момент времени.
(~N_m = lim_{Delta t to 0} frac{A}{Delta t} = A’ .)
Любой двигатель или механизм предназначены для выполнения определенной механической работы, которую называют полезной работой Ap. Но любой машине приходится совершать большую работу, так как вследствие действия сил трения часть подводимой к машине энергии не может быть преобразована в механическую работу. Поэтому эффективность работы машины характеризуют коэффициентом полезного действия η (КПД).
Коэффициент полезного действия η — это отношение полезной работы Ap, совершенной машиной, ко всей затраченной работе Az (подведенной энергии W):
(~eta = frac{A_p}{A_z} = frac{A_p}{W} = frac{N_p}{N_z},)
где Np, Nz — полезная и затраченная мощности соответственно. КПД обычно выражают в процентах.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 63-64.
Мощность
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени:
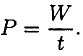
Единицы измерения мощности: ватты, киловатты,
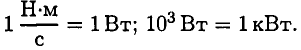
Мощность при поступательном движении (рис. 16.1)
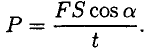
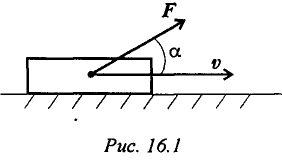
Учитывая, что
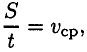
получим
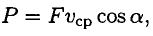
где 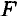
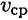
Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Мощность при вращении (рис. 16.2)
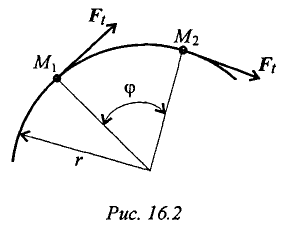
Тело движется по дуге радиус 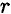
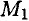
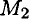
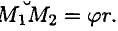
Работа силы:
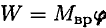
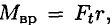
где 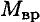
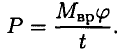
Учитывая, что 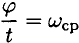
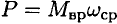
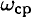
Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость.
Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
Условие задачи:
Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность, развиваемую тепловозом за это время, если масса тепловоза 600 тонн, а коэффициент трения 0,005.
Задача №2.7.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(t=5) мин, (upsilon=72) км/ч, (m=600) т, (k=0,005), (N_{ср}-?)
Решение задачи:
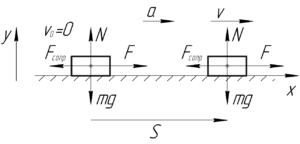
[A = FS]
Тогда среднюю мощность (N_{ср}), определяемую как отношение совершенной работы ко времени, можно узнать по следующей формуле:
[{N_{ср}} = frac{A}{t} = Ffrac{S}{t};;;;(1)]
Сначала разберёмся с кинематикой. Если тепловоз движется равноускоренно без начальной скорости и за время (t) набирает скорость (upsilon), то ускорение тепловоза найдем из следующих соображений:
[upsilon = at;;;;(2)]
[a = frac{upsilon }{t};;;;(3)]
При этом он пройдет следующий путь:
[S = frac{{a{t^2}}}{2}]
Принимая во внимание равенство (2), получим:
[S = frac{{upsilon t}}{2};;;;(4)]
Для определения величины силы тяги запишем второй закон Ньютона в проекции на ось (x):
[F – {F_{сопр}} = ma]
Видно, что (N=mg) по первому закону Ньютона в проекции на ось (y). Поэтому силу сопротивления (F_{сопр}) найдем по формуле:
[{F_{сопр}} = kN = kmg]
[F – kmg = ma]
[F = mleft( {a + kg} right)]
Подставим в эту формулу выражение (3), а полученное выражение и (4) – в формулу (1). В итоге имеем такое решение задачи в общем виде:
[{N_{ср}} = mleft( {frac{upsilon }{t} + kg} right)frac{upsilon }{2}]
Переведем некоторые данные задачи в систему СИ:
[5;мин = 5 cdot 60;с = 300;с]
[72;км/ч = frac{{72 cdot 1000}}{{1 cdot 3600}};м/с = 20;м/с]
[600;т = 600 cdot {10^3};кг = 6 cdot {10^5};кг]
Последнее действие – считаем ответ:
[{N_{ср}} = 6 cdot {10^5} cdot left( {frac{{20}}{{300}} + 0,005 cdot 10} right) cdot frac{{20}}{2} = 700000;Вт = 700;кВт]
Ответ: 700 кВт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.34 Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью
2.7.36 Укажите график зависимости потенциальной энергии свободно падающего тела
2.7.37 Уравнение движения материальной точки имеет вид: x=t^2-2t^3 (м). Определите
«Не стыдно не знать,
стыдно не учиться»
В данной теме будут рассмотрены примеры решения задач на
расчет механической работы и мощности.
Задача 1. Двигатели электропоезда при движении с
постоянной скоростью 54 км/ч потребляют мощность 900 кВт. Определите силу тяги
двигателей, если их КПД составляет 80%. Какую работу совершила сила тяги
двигателей за 30 мин движения поезда?
|
ДАНО: |
СИ |
РЕШЕНИЕ: Коэффициент полезного действия — это есть отношение Мощность — это работа, отнесенная к единице времени, Сила тяги двигателей: Полезная работа двигателей: |
|
|
Ответ: 48 кН; 1,3 ГДж.
Задача 2. Какую работу надо совершить, чтобы
равномерно передвинуть ящик на 9 м по полу, прилагая усилие, направленное под
углом 30о к горизонту? Сила тяжести ящика 500 Н, а коэффициент
трения скольжения ящика о пол 0,2.
|
ДАНО: |
РЕШЕНИЕ: Механическая работа определяется по формуле Запишем второй закон Ньютона для рассматриваемого случая В проекциях на ось Ох В проекциях на ось О Сила трения определяется по формуле Тогда получаем Преобразуем последнее выражение Тогда механическая работа равна |
|
|
Ответ: 807 Дж.
Задача 3. Поезд, масса которого 784 т, начинает
двигаться в гору и за 50 с развивает скорость 5 м/с. Коэффициент сопротивления
движению равен 0,005, уклон горы — 0,005. Определите среднюю мощность
локомотива, считая силу сопротивления пропорциональной силе нормальной реакции
рельсов.
|
ДАНО: |
РЕШЕНИЕ: Строго говоря, в данном примере поезд нельзя принимать за Если считать силу тяги, развиваемую локомотивом, Запишем второй закон Ньютона в общем виде В проекциях на ось Оx: В проекциях на ось Оy: Сила трения определяется по формуле Тогда получаем Из кинематики равноускоренного движения
Тогда, средняя мощность локомотива, с учётом того, что
|
|
|
Ответ: 200 кВт.
Задача 4. На горизонтальной поверхности лежит брусок
массой 11 кг, к которому прикреплена пружина жесткостью 200 Н/м. Коэффициент
трения между бруском и поверхностью 0,1. К свободному концу пружины
прикладывают направленную под углом 45о к горизонту силу, под действием
которой брусок равномерно перемещается на 0,5 м. Определите совершенную при
этом работу.
|
ДАНО: |
РЕЩЕНИЕ: Под действием силы, приложенной к пружине, происходит Основное уравнение динамики при равномерном прямолинейном В проекциях на Ох: В проекциях на Оу: Тогда сила трения равна Тогда Тогда приложенная к концу пружины сила равна Из закона Гука выражим удлинение пружины Тогда полная работа равна |
|
|
Ответ: 5,5 Дж.

