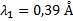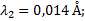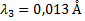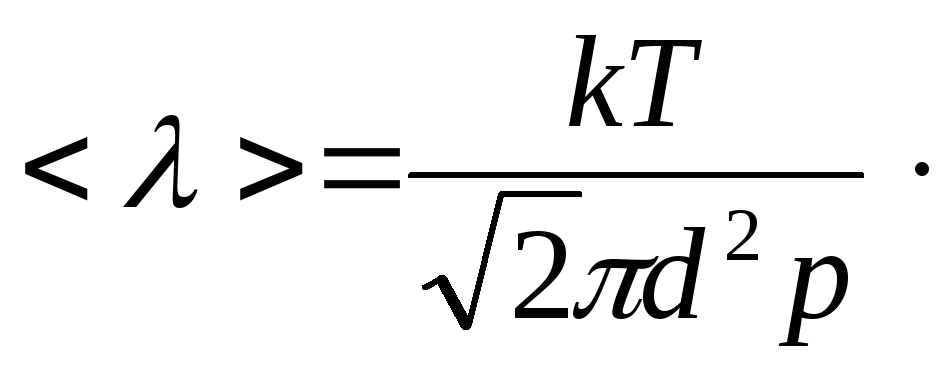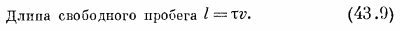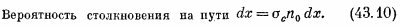Измерьте среднюю длину своего шага. Пользуясь этой мерой, определите путь, который вы проходите от своего дома до ближайшей остановки автобуса.
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §14. Задание. Номер №1
Решение
Получай решения и ответы с помощью нашего бота
Допустим длина шага (l) равна 50 см.
Количество шагов от дома до ближайшей остановки автобуса (N) − 250.
Расстояние от дома до остановки (S) = l * N;
S = 50 * 250 = 12 500 см = 125 м.
Ответ. 125 м.
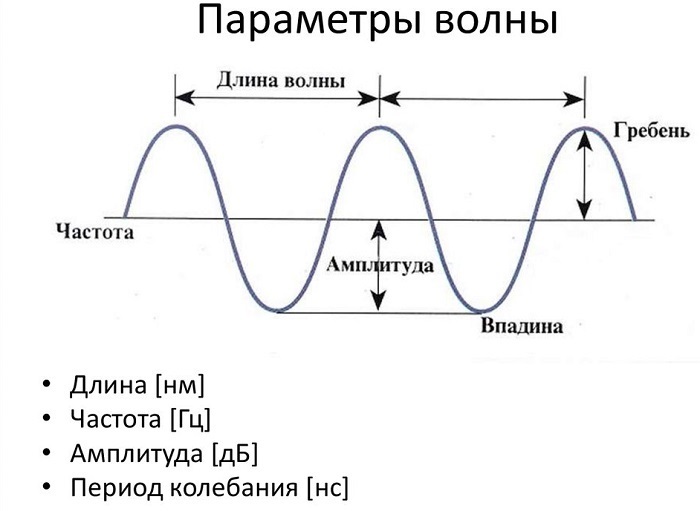
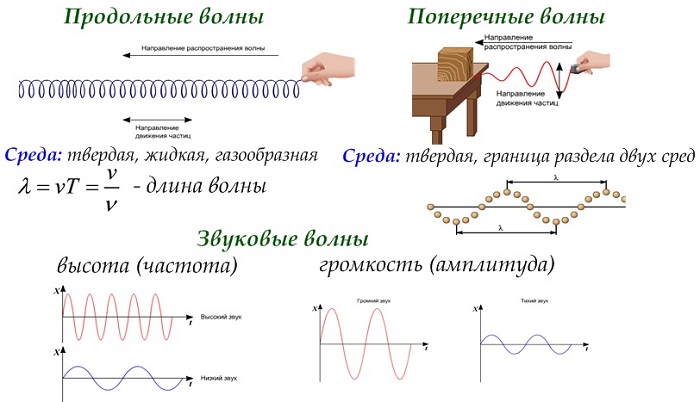
Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
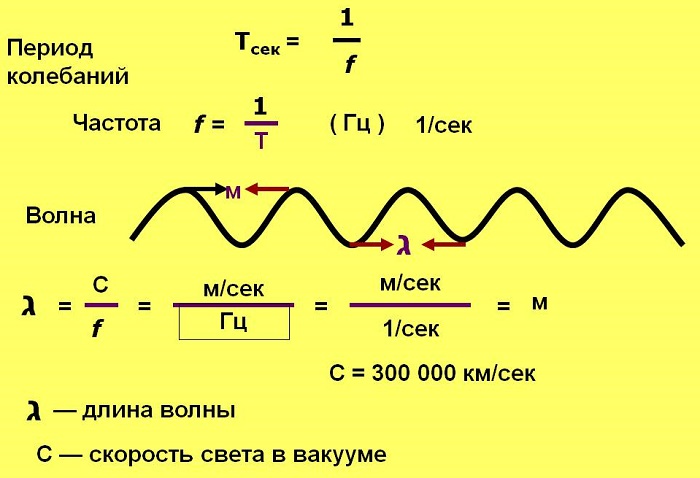
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
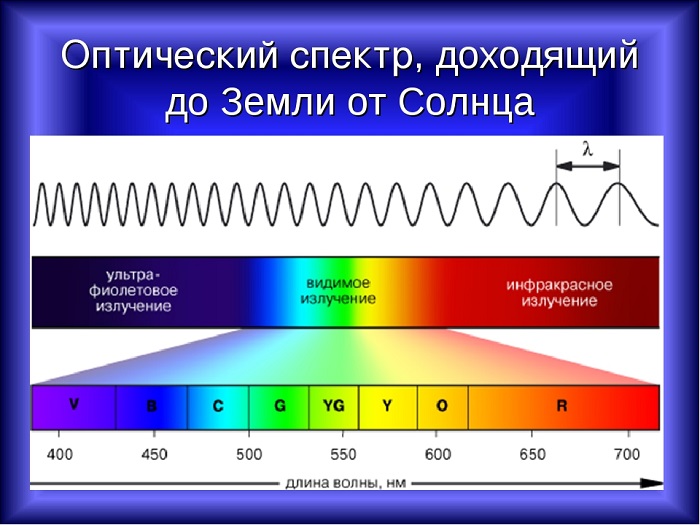
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
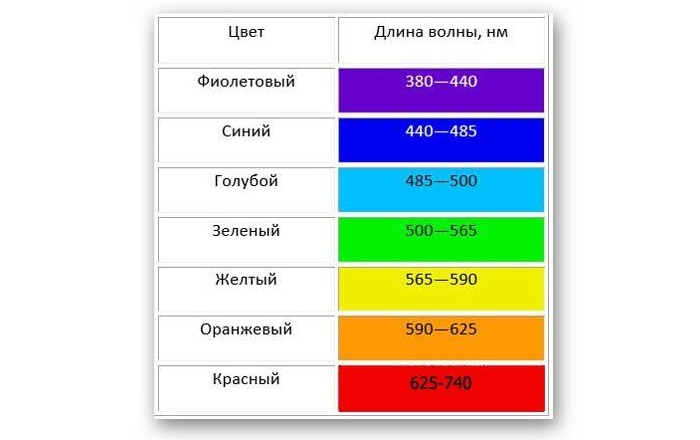
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
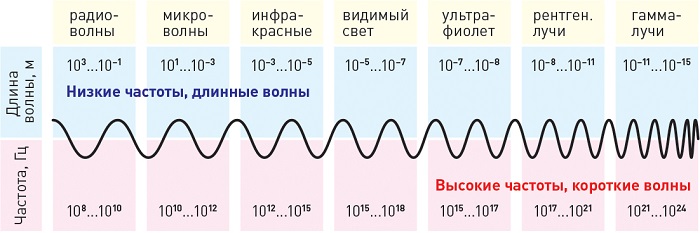
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
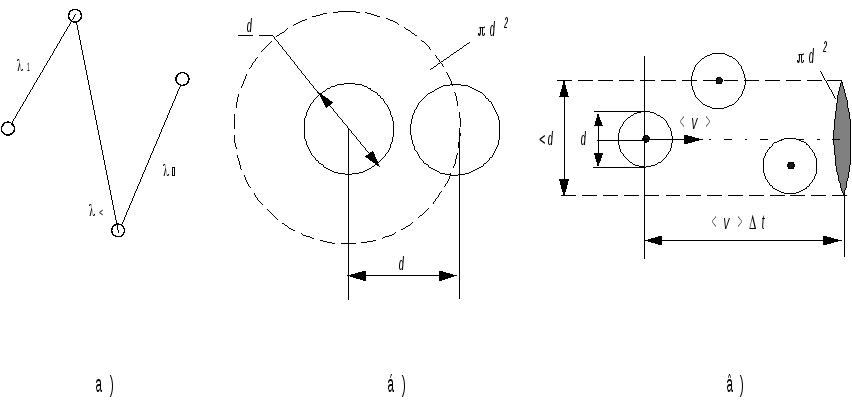
Рис. 19.1
Молекулы газа,
находясь в тепловом движении, непрерывно
сталкиваются друг с другом. Между двумя
последовательными соударениями молекулы,
двигаясь равномерно и прямолинейно,
проходят некоторые расстояния, называемые
длинами свободных пробегов
(рис. 19.1.а). Эти расстояния могут быть
самыми разными, то есть
— случайная величина. Поэтому
вводят понятие средней длины свободного
пробега <>,
под которой понимают среднее расстояние,
проходимое молекулой между двумя
последовательными столкновениями со
средней арифметической скоростью <V>.
Будем
считать, что молекулы газа представляют
собой шарики диаметром d.
Минимальное расстояние
(рис.19.1.б), на
которое могут сблизиться при столкновении
центры двух молекул, также равно d.
Это расстояние
называется эффективным диаметром
молекулы.
Круг радиусом d
с центром в центре рассматриваемой
молекулы площадью d2
называется эффективным
сечением молекулы.
Если
молекула за некоторый промежуток времени
t
претерпевает в среднем <V>
столкновений, то средняя длина ее
свободного пробега равна
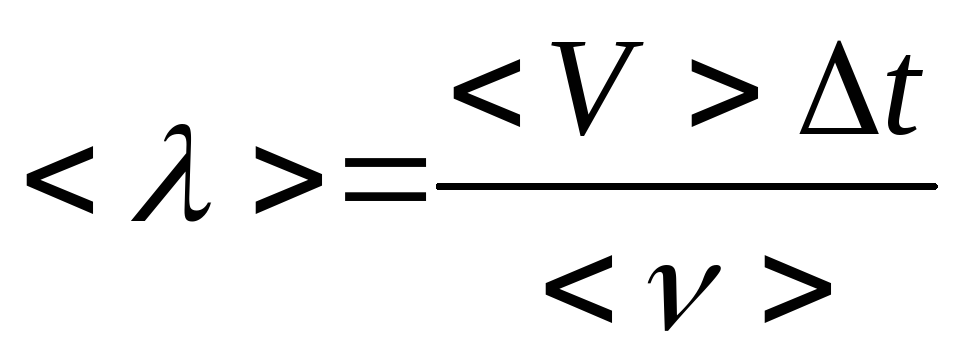
(19.1)
Предположим
для простоты, что движется только одна
рассматриваемая молекула, а остальные
неподвижны. Кроме того, ломаную траекторию
молекулы мысленно спрямим и будем
считать движение молекул условно
прямолинейным (рис.19.1.в).
Тогда за время t
эта молекула претерпит <>
столкновений, равное числу молекул,
центры которых лежат в прямом цилиндре
с основанием, равным эффективному
сечению молекулы, и высотой, равной
пути, проходимому молекулой за это
время, то есть <V>t:
,
где
n
— концентрация молекул, V
— объем цилиндра.
Учитывая,
что
,
получим
.
На
самом же деле движутся все молекулы, и
число столкновений определяется не
средней арифметической скоростью
молекул (то есть средней скоростью по
отношению к стенкам сосуда), а средней
скоростью их движения по отношению друг
к другу <Vотн.>,
которая, как можно показать, больше
средней арифметической скорости
раз, то есть
.
Поэтому
при учете движения всех молекул среднее
число столкновений, испытываемых одной
молекулой за некоторый промежуток
времени t,
равно
,
(19.2)
а в единицу времени
.
(19.3)
Подставляя
выражение(19.2) в (19.1), получим выражение
для средней длины свободного пробега
молекулы:
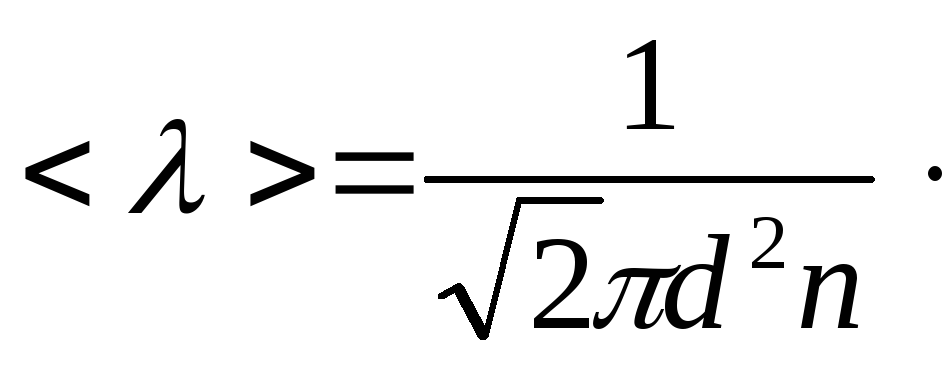
Используется
и иная
форма
записи выражения для <>,
для получения которой нужно в выражение
(19.4) подставить n
из уравнения (15.26), тогда
(19.5)
Из
выражения (19.5) следует, что с
ростом давления газа p
средняя длина свободного пробега
уменьшается.
Для примера укажем, что при нормальных
условиях (p105Па,
Т=273К) молекулы
кислорода движутся со средней скоростью
порядка 500 м/с, имеют среднюю длину
свободного пробега около 2*10-7м
и совершают приблизительно 2,5.109
столкновений в секунду каждая. В табл.19.1
приведены значения <>
для молекул кислорода при Т
=293 К и различных давлениях.
Таблица
19.1
|
<> |
P |
|
|
м |
Па |
мм.рт.ст. |
|
6,21*10-8 |
1,012*105 |
760 |
|
4,72*10-5 |
1,333*102 |
1 |
|
4,72*10-3 |
1,333 |
10-2 |
|
4,72*10-1 |
1,333*10-2 |
10-4 |
|
4,72*102 |
1,333*10-5 |
10-7 |
Как
следует из таблицы, при малых давлениях
значение <>
может быть больше размеров области
(сосуда), в которой находится газ; в этом
случае молекулы движутся от одной стенки
сосуда до другой практически без
столкновений друг с другом.
Физическим
вакуумом называется состояние газа,
при котором средняя длина свободного
пробега его молекул соизмерима с
линейными размерами сосуда, содержащего
газ.
Из
сказанного следует, что понятие
вакуума относительно.
Чем больше размер сосуда, тем меньше
давление, при котором наступает состояние
вакуума, и наоборот. Например, для газа,
заключенного в пористых телах с диаметром
пор менее 10-7м,
состояние при атмосферном давлении уже
можно считать вакуумом, так как молекулы
газа будут проходить сквозь эти поры,
ударяясь о их стенки и не сталкиваясь
друг с другом. В электронной лампе,
размеры которой порядка нескольких
сантиметров, состояние вакуума наступает
при давлении 10-7Па,
а в электронно-лучевой трубке с линейными
размерами в десятки сантиметров вакуум
наступает при давлении порядка 10-4
Па.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 43. Диффузия
Средняя длина свободного пробега
Есть еще возможность описать столкновения молекул, не вводя для этого времени между столкновениями. Можно определить, далеко ли успеет уйти частица между столкновениями. Если мы знаем, что среднее время между столкновениями равно τ, а средняя скорость молекул равна v, то очевидно, что среднее расстояние между столкновениями, которое мы обозначим буквой l, равно произведению τ и v. Это расстояние между столкновениями обычно называют длиной свободного пробега:
В этой главе мы не будем уточнять, какого рода среднее мы имеем в виду в каждом случае. Существующие разные средние — среднее, корень из среднего квадрата и т. д.— приблизительно равны и отличаются только множителями, близкими к единице. Поскольку для получения правильных множителей необходим подробный анализ, нам нет смысла очень уж стараться уточнять, какое именно среднее используется в том или ином случае. Мы хотим еще предупредить читателей, что используемые для обозначения физических величин алгебраические символы (например, l для длины свободного пробега) не являются общепринятыми просто потому, что об этом никто еще специально не договаривался.
Вероятность того, что молекула испытает столкновение, пройдя расстояние dx, равна dx/l, как вероятность столкновения за короткий промежуток времени dt равна dt/τ. Призвав на помощь те же аргументы, что и раньше, читатель сможет показать, что вероятность того, что молекула пройдет по крайней мере расстояние x, прежде чем испытает следующее столкновение, равна е-х/l.
Среднее расстояние, которое молекула проходит между столкновениями (длина свободного пробега l), зависит от количества молекул, ее окружающих, и от того, какого «размера» эти молекулы, т. е. от того, насколько уязвимую мишень представляют они собой. «Размеры» мишени при столкновениях обычно описывают при помощи «эффективного сечения столкновений»; эта же идея используется и в ядерной физике или в задачах о рассеянии света.
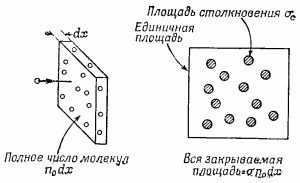
Под «эффективным сечением столкновения» понимается площадь, в которую должен попасть центр частицы, если она должна столкнуться с заданной молекулой. Если молекулы выглядят как маленькие шарики (классическая картина), то следует ожидать, что σс=π(r1 +r2)2, где r1 и r2— радиусы двух сталкивающихся молекул. Вероятность того, что наша частица столкнется с какой-нибудь молекулой, равна отношению площади, покрываемой рассеивающими молекулами, к полной площади, принятой нами за единицу. Таким образом, вероятность столкновения на пути dx равна σcn0dx:
Мы уже отметили раньше, что вероятность столкновения на пути dx может быть записана в терминах длины свободного пробега l как dx/l. Сравнивая это с (43.10), можно связать длину свободного пробега с эффективным сечением столкновения:
Это равенство легче запомнить, если записать его так:
Эта формула говорит, что если частица проходит путь l внутрь рассеивателя, в котором молекулы могут как раз покрыть всю площадь, то в среднем происходит одно столкновение. В цилиндре высотой l, поставленном на основание единичной площади, содержится n0l рассеивателей; если каждый из них занимает площадь σс, то полная площадь, покрытая ими, равна n0lσс, а это как раз единичая площадь. Конечно, молекулы не покрывают всей площади целиком, потому что часть молекул прячется за соседние молекулы. Поэтому некоторые молекулы пройдут между столкновениями большее, чем l, расстояние. Ведь это только в среднем молекулам между столкновениями дается ровно столько времени, чтобы они смогли пройти расстояние l. Измеряя длину свободного пробега l, можно определить эффективное сечение рассеяния σс и сравнить этот результат с расчетами, основанными на детальной теории строения атомов. Но это уже совсем другая тема! А пока вернемся к проблеме неравновесных состояний.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
Задача 1
Чему равна длина волны де Бройля электрона при скорости 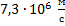
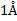
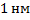
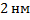
Дано: 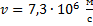
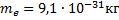
Найти: 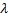
Решение
Для решения задачи применяем уравнение де Бройля:
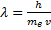
где 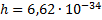
Подставляем в данное уравнение числовые данные:
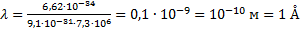
Ответ: 1.
Задача 2
Найти среднюю длину волны атома водорода при температуре 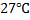
Дано: 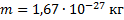
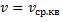
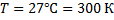
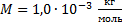
Найти: 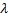
Решение
Уравнение корпускулярно-волнового дуализма де Бройля:
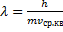
где 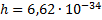
Из курса молекулярной физики известно, что средняя квадратичная скорость равна:
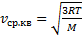
где 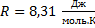
Следовательно, длина волны равна:
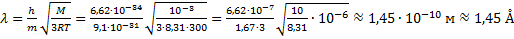
Ответ:
Задача 3
Найти длину волны электрона, ускоренного разностью потенциалов 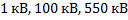
Дано: 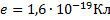
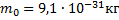
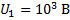
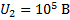
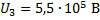
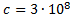
Найти: 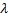
Решение
Для решения задачи применяем уравнение де Бройля:
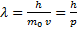
Из курса электродинамики известна формула работы электрического поля, которая идет на повышение кинетической энергии электрона:
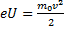
Из этого уравнения выражаем скорость, которую получает электрон в электрическом поле:
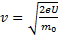
Если провести расчёт, то можно увидеть что при напряжении 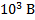
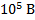
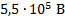
1. Вычислим длину волны для первого напряжения.
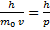
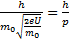
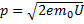
Подставляем его в уравнение де Бройля:
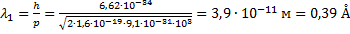
2. Для выведения формулы импульса в релятивистском случае вспомним выражение полной энергии из раздела «Основы теории относительности».
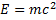
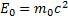
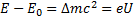
То есть ускоряющее электрическое поле совершило работу 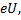
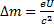
Если 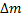
Если 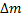
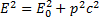
Из этого выражения необходимо выразить импульс p:
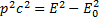
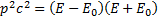
Так как
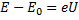
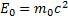
То:
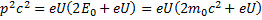
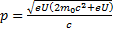
Подставляем выражение для импульса в уравнение де Бройля:
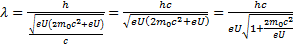
В данную формулу подставляем физические постоянные:
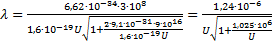
Мы получили формулу вычисления длины волны электрона в релятивистском случае при любом значении напряжения.
3. Для напряжения 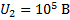
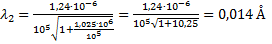
Для напряжения 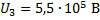
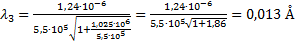
Ответ: