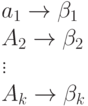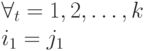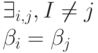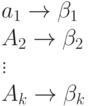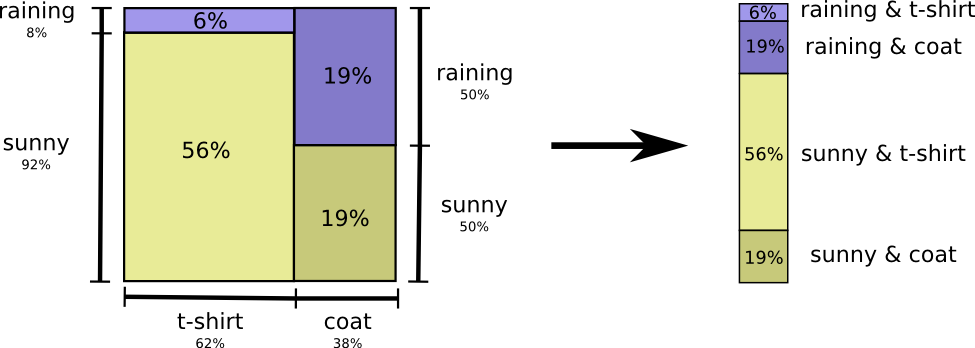Как найти среднюю длину кодовых слов

Неравномерное кодирование. Средняя длина кодирования

В приведенных выше
примерах кодирования все кодовые слова
имели одинаковую длину. Однако это не
является обязательным требованием.
Более того, если вероятности появления
сообщений заметно отличаются друг от
друга, то сообщения с большой вероятностью
появления лучше кодировать короткими
словами, а более длинными словами
кодировать редкие сообщений. В результате
кодовый текст при определенных условиях
станет в среднем короче.

Показателем
экономичности или эффективности
неравномерного кода является не длина
отдельных кодовых слов, а «средняя»
их длина, определяемая равенством:

где
—
кодовое слово, которым закодировано
сообщение,
а—
его длина,—
вероятность сообщения,—
общее число сообщений источника.
Для краткости записи формул далее могут
использоваться обозначенияи.
Заметим, что обозначение средней длины
кодирования черезподчеркивает
тот факт, что эта величина зависит как
отисточника
сообщений
,
так и от способа кодирования.

Наиболее экономным
является код с наименьшей средней длиной
.
Сравним на примерах экономичность
различных способов кодирования одного
и того же источника.

Пусть источник
содержит 4 сообщения
с
вероятностями.
Эти сообщения можно закодировать
кодовыми словами постоянной длины,
состоящими из двух знаков, в алфавитев
соответствии с кодовой таблицей.

	00
	01
A_3	10
A_4	11

Очевидно, что для
представления (передачи) любой
последовательности в среднем потребуется
2 знака на одно сообщение. Сравним
эффективность такого кодирования с
описанным выше кодированием словами
переменной длины. Кодовая таблица для
данного случая может иметь следующий
вид.

	0
	1
	10
	11

В этой таблице, в
отличие от предыдущей, наиболее частые
сообщения
икодируются
одним двоичным знаком. Для последнего
варианта кодирования имеем

в то время как для
равномерного кода средняя длина
(она
совпадает с общей длиной кодовых слов).
Из рассмотренного примера видно, что
кодирование сообщений словами различной
длины может дать суще-ственное (почти
в два раза) увеличение экономичности
кодирования.

При использовании
неравномерных кодов появляется проблема,
которую поясним на примере последней
кодовой таблицы. Пусть при помощи этой
таблицы кодируется последовательность
сообщений
,
в результате чего она преобразуется в
следующий двоичный текст: 010110. Первый
знак исходного сообщения декодируется
однозначно — это.
Однако дальше начинается неопределенность:или.
Это лишь некоторые из возможных вариантов
декодирования исходной последовательности
знаков.

Необходимо отметить,
что неоднозначность декодирования
слова появилась несмотря на то, что
условие однозначности декодирования
знаков (инъективность кодового
отображения) выполняется.

Существо проблемы
— в невозможности однозначного выделения
кодовых слов. Для ее решения следовало
бы отделить одно кодовое слово от
другого. Разумеется, это можно сделать,
но лишь используя либо паузу между
словами, либо специальный разделительный
знак, для которого необходимо особое
кодовое обозначение. И тот, и другой
путь, во-первых, противоречат описанному
выше способу кодирования слов путем
конкатенации кодов
знаков,
образующих слово, и, во-вторых, приведет
к значительному удлинению кодового
текста, сводя на нет преимущества
использования кодов переменной длины.

Решение данной
проблемы заключается в том, чтобы иметь
возможность в любом кодовом тексте
выделять отдельные кодовые слова без
использования специальных разделительных
знаков. Иначе говоря, необходимо, чтобы
код удовлетворял следующему требованию:
всякая последовательность кодовых
знаков может быть единственным образом
разбита на кодовые слова. Коды, для
которых последнее требование выполнено,
называются однозначно декодируемыми
(иногда их называют кодами без запятой).

Рассмотрим код
(схему алфавитного кодирования)
,
заданный кодовой таблицей

и различные слова,
составленные из элементарных кодов.

Определение.
Код
называется
однозначно декодируемым, если

то есть любое слово,
составленное из элементарных кодов,
единственным образом разлагается на
элементарные коды.

Если таблица кодов
содержит одинаковые кодовые слова, то
есть если

то код заведомо не
является однозначно декодируемым (схема
не является разделимой). Такие коды
далее не рассматриваются.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Кодирование Хаффмана (часть 1 и 2)

Дата публикации 20 авг 2017

| Редактировалось 10 янв 2018

Кодирование Хаффмана. Часть 1.
Вступление
Здравствуй, дорогой читатель! В данной статье будет рассмотрен один из способов сжатия данных. Этот способ является достаточно широко распространённым и заслуживает определённого внимания. Данный материал рассчитан по объёму на три статьи, первая из которых будет посвящена алгоритму сжатия, вторая — программной реализации алгоритма, а третья ― декомпрессии. Алгоритм сжатия будет написан на языке C++, алгоритм декомпрессии ― на языке Assembler.
Однако, перед тем, как приступить к самому алгоритму, следует включить в статью немного теории.
Немного теории
Компрессия (сжатие) ― способ уменьшения объёма данных с целью дальнейшей их передачи и хранения.
Декомпрессия ― это способ восстановления сжатых данных в исходные.
Компрессия и декомпрессия могут быть как без потери качества (когда передаваемая/хранимая информация в сжатом виде после декомпрессии абсолютно идентична исходной), так и с потерей качества (когда данные после декомпрессии отличаются от оригинальных). Например, текстовые документы, базы данных, программы могут быть сжаты только способом без потери качества, в то время как картинки, видеоролики и аудиофайлы сжимаются именно за счёт потери качества исходных данных (характерный пример алгоритмов ― JPEG, MPEG, ADPCM), при порой незаметной потере качества даже при сжатии 1:4 или 1:10.
Выделяются основные виды упаковки:

Десятичная упаковка предназначена для упаковки символьных данных, состоящих только из чисел. Вместо используемых 8 бит под символ можно вполне рационально использовать всего лишь 4 бита для десятичных и шестнадцатеричных цифр, 3 бита для восьмеричных и так далее. При подобном подходе уже ощущается сжатие минимум 1:2.

Относительное кодирование является кодированием с потерей качества. Оно основано на том, что последующий элемент данных отличается от предыдущего на величину, занимающую в памяти меньше места, чем сам элемент. Характерным примером является аудиосжатие ADPCM (Adaptive Differencial Pulse Code Modulation), широко применяемое в цифровой телефонии и позволяющее сжимать звуковые данные в соотношении 1:2 с практически незаметной потерей качества.

Символьное подавление — способ сжатия информации, при котором длинные последовательности из идентичных данных заменяются более короткими.

Статистическое кодирование основано на том, что не все элементы данных встречаются с одинаковой частотой (или вероятностью). При таком подходе коды выбираются так, чтобы наиболее часто встречающемуся элементу соответствовал код с наименьшей длиной, а наименее частому ― с наибольшей.

Кроме этого, коды подбираются таким образом, чтобы при декодировании можно было однозначно определить элемент исходных данных. При таком подходе возможно только бит-ориентированное кодирование, при котором выделяются разрешённые и запрещённые коды. Если при декодировании битовой последовательности код оказался запрещённым, то к нему необходимо добавить ещё один бит исходной последовательности и повторить операцию декодирования. Примерами такого кодирования являются алгоритмы Шеннона и Хаффмана, последний из которых мы и будем рассматривать.
Конкретнее об алгоритме
Как уже известно из предыдущего подраздела, алгоритм Хафмана основан на статистическом кодировании. Разберёмся поподробнее в его реализации.
Пусть имеется источник данных, который передаёт символы [math](a_1, a_2, …, a_n)[/math] с разной степенью вероятности, то есть каждому [math]a_i[/math] соответствует своя вероятность (или частота) [math]P_i(a_i)[/math], при чём существует хотя бы одна пара [math]a_i[/math] и [math]a_j[/math] ,[math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] не равны. Таким образом образуется набор частот [math]{P_1(a_1), P_2(a_2),…,P_n(a_n)}[/math], при чём [math]displaystyle sum_{i=1}^{n} P_i(a_i)=1[/math], так как передатчик не передаёт больше никаких символов кроме как [math]{a_1,a_2,…,a_n}[/math].
Наша задача ― подобрать такие кодовые символы [math]{b_1, b_2,…,b_n}[/math] с длинами [math]{L_1(b_1),L_2(b_2),…,L_n(b_n)}[/math], чтобы средняя длина кодового символа не превышала средней длины исходного символа. При этом нужно учитывать условие, что если [math]P_i(a_i)>P_j(a_j)[/math] и [math]ine j[/math], то [math]L_i(b_i)le L_j(b_j)[/math].
Хафман предложил строить дерево, в котором узлы с наибольшей вероятностью наименее удалены от корня. Отсюда и вытекает сам способ построения дерева:
1. Выбрать два символа [math]a_i[/math] и [math]a_j[/math], [math]ine j[/math], такие, что [math]P_i(a_i)[/math] и [math]P_j(a_j)[/math] из всего списка [math]{P_1(a_1),P_2,…,P_n(a_n)}[/math] являются минимальными.
2. Свести ветки дерева от этих двух элементов в одну точку с вероятностью [math]P=P_i(a_i)+P_j(a_j)[/math], пометив одну ветку нулём, а другую ― единицей (по собственному усмотрению).
3. Повторить пункт 1 с учётом новой точки вместо [math]a_i[/math] и [math]a_j[/math], если количество получившихся точек больше единицы. В противном случае мы достигли корня дерева.
Теперь попробуем воспользоваться полученной теорией и закодировать информацию, передаваемую источником, на примере семи символов.
Разберём подробно первый цикл. На рисунке изображена таблица, в которой каждому символу [math]a_i[/math] соответствует своя вероятность (частота) [math]P_i(a_i)[/math]. Согласно пункту 1 мы выбираем два символа из таблицы с наименьшей вероятностью. В нашем случае это [math]a_1[/math] и [math]a_4[/math]. Согласно пункту 2 сводим ветки дерева от [math]a_1[/math] и [math]a_4[/math] в одну точку и помечаем ветку, ведущую к [math]a_1[/math], единицей, а ветку, ведущую к [math]a_4[/math],― нулём. Над новой точкой приписываем её вероятность (в данном случае ― 0.03) В дальнейшем действия повторяются уже с учётом новой точки и без учёта [math]a_1[/math] и [math]a_4[/math].

После многократного повторения изложенных действий выстраивается следующее дерево:

По построенному дереву можно определить значение кодов [math]{b_1,b_2,…,b_n}[/math], осуществляя спуск от корня к соответствующему элементу [math]a_i[/math], при этом приписывая к получаемой последовательности при прохождении каждой ветки ноль или единицу (в зависимости от того, как именуется конкретная ветка). Таким образом таблица кодов выглядит следующим образом:

i b_i L_i(b_i)

1 011111 6

2 1 1

3 0110 4

4 011110 6

5 010 3

6 00 2

7 01110 5

Теперь попробуем закодировать последовательность из символов.
Пусть символу [math]a_i[/math] соответствует (в качестве примера) число [math]i[/math]. Пусть имеется последовательность 12672262. Нужно получить результирующий двоичный код.
Для кодирования можно использовать уже имеющуюся таблицу кодовых символов [math]b_i[/math] при учёте, что [math]b_i[/math] соответствует символу [math]a_i[/math]. В таком случае код для цифры 1 будет представлять собой последовательность 011111, для цифры 2 ― 1, а для цифры 6 ― 00. Таким образом, получаем следующий результат:

Данные 1 2 6 7 2 2 6 2 Длина кода

Исходные 001 010 110 111 010 010 110 010 24 бит

Кодированные 011111 1 00 01110 1 1 00 1 19 бит

В результате кодирования мы выиграли 5 бит и записали последовательность 19 битами вместо 24.
Однако это не даёт полной оценки сжатия данных. Вернёмся к математике и оценим степень сжатия кода. Для этого понадобится энтропийная оценка.
Энтропия ― мера неопределённости ситуации (случайной величины) с конечным или с чётным числом исходов. Математически энтропия формулируется как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятых с обратным знаком:

[math]H(X)=-displaystyle sum_{i=1}^{n}P_icdot log_d (P_i)[/math].

Где [math]X[/math] ― дискретная случайная величина (в нашем случае ― кодовый символ), а [math]d[/math] ― произвольное основание, большее единицы. Выбор основания равносилен выбору определённой единицы измерения энтропии. Так как мы имеем дело с двоичными цифрами, то в качестве основания рационально выбрать [math]d=2[/math].
Таким образом, энтропию для нашего случая можно представить в виде:

[math]H(b)=-displaystyle sum_{i=1}^{n}P_i(a_i)cdot log_2 (P_i(a_i))[/math].

Энтропия обладает замечательным свойством: она равна минимальной допустимой средней длине кодового символа [math]overline{L_{min}}[/math] в битах. Сама же средняя длина кодового символа вычисляется по формуле

[math]overline{L(b)}=displaystyle sum_{i=1}^{n}P_i(a_i)cdot L_i(b_i)[/math].

Подставляя значения в формулы [math]H(b)[/math] и [math]overline{L(b)}[/math], получаем следующий результат: [math]H(b)=2,048[/math], [math]overline{L(b)}=2,100[/math].
Величины [math]H(b)[/math] и [math]overline{L(b)}[/math] очень близки, что говорит о реальном выигрыше в выборе алгоритма. Теперь сравним среднюю длину исходного символа и среднюю длину кодового символа через отношение:

[math]frac{overline{L_{src}}}{L(b)}=frac{3}{2,1}=1,429[/math].

Таким образом, мы получили сжатие в соотношении 1:1,429, что очень неплохо.
И напоследок, решим последнюю задачу: дешифровка последовательности битов.
Пусть для нашей ситуации имеется последовательность битов:

001101100001110001000111111

Необходимо определить исходный код, то есть декодировать эту последовательность.
Конечно, в такой ситуации можно воспользоваться таблицей кодов, но это достаточно неудобно, так как длина кодовых символов непостоянна. Гораздо удобнее осуществить спуск по дереву (начиная с корня) по следующему правилу:
1. Исходная точка ― корень дерева.
2. Прочитать новый бит. Если он ноль, то пройти по ветке, помеченной нулём, в противном случае ― единицей.
3. Если точка, в которую мы попали, конечная, то мы определили кодовый символ, который следует записать и вернуться к пункту 1. В противном случае следует повторить пункт 2.
Рассмотрим пример декодирования первого символа. Мы находимся в точке с вероятностью 1,00 (корень дерева), считываем первый бит последовательности и отправляемся по ветке, помеченной нулём, в точку с вероятностью 0,60. Так как эта точка не является конечной в дереве, то считываем следующий бит, который тоже равен нулю, и отправляемся по ветке, помеченной нулём, в точку [math]a_6[/math], которая является конечной. Мы дешифровали символ ― это число 6. Записываем его и возвращаемся в исходное состояние (перемещаемся в корень).
Таким образом декодированная последовательность принимает вид.

Данные 001101100001110001000111111 Длина кода

Кодированные 00 1 1 0110 00 01110 00 1 00 011111 1 27 бит

Исходные 6 2 2 3 6 7 6 2 6 1 2 33 бит

В данном случае выигрыш составил 6 бит при достаточно небольшой длине последовательности.
Вывод напрашивается сам собой: алгоритм прост. Однако следует сделать замечание: данный алгоритм хорош для сжатия текстовой информации (действительно, реально мы используем при набивке текста примерно 60 символов из доступных 256, то есть вероятность встретить иные символы близка к нулю), но достаточно плох для сжатия программ (так как в программе все символы практически равновероятны). Так что эффективность алгоритма очень сильно зависит от типа сжимаемых данных.
Постскриптум
В этой статье мы рассмотрели алгоритм кодирования по методу Хаффмана, который базируется на неравномерном кодировании. Он позволяет уменьшить размер передаваемых или хранимых данных. Алгоритм прост для понимания и может давать реальный выигрыш. Кроме этого, он обладает ещё одним замечательным свойством: возможность кодировать и декодировать информацию «на лету» при условии того, что вероятности кодовых слов правильно определены. Хотя существует модификация алгоритма, позволяющая изменять структуру дерева в реальном времени.
В следующей части статьи мы рассмотрим байт-ориентированное сжатие файлов с использованием алгоритма Хаффмана, реализованное на C++.
Кодирование Хаффмана. Часть 2
Вступление
В прошлой части мы рассмотрели алгоритм кодирования, описали его математическую модель, произвели кодирование и декодирование на конкретном примере, рассчитали среднюю длину кодового слова, а также определили коэффициент сжатия. Кроме этого, были сделаны выводы о преимуществах и недостатках данного алгоритма.
Однако, помимо этого неразрешёнными остались ещё два вопроса: реализация программы, сжимающей файл данных, и программы, распаковывающей сжатый файл. Первому вопросу и посвящена настоящая статья. Поэтому следует заняться проектированием.
Проектирование
Первым делом необходимо посчитать частоты вхождения символов в файл. Для этого опишем следующую структуру:

// Структура для подсчёта частоты символа

Эта структура будет описывать каждый символ из 256. ch ― сам ASCII-символ, freq ― количество вхождений символа в файл. Поле table ― указатель на структуру:

Как видно, TTable ― это описатель узла с разветвлением по нулю и единице. При помощи этих структур в дальнейшем и будет осуществляться построение дерева компрессии. Теперь объявим для каждого символа свою частоту и свой узел:

Попробуем разобраться, каким образом будет осуществляться построение дерева. На начальной стадии программа должна осуществить проход по всему файлу и подсчитать количество вхождений символов в него. Помимо этого, для каждого найденного символа программа должна создать описатель узла. После этого из созданных узлов с учётом частоты символов программа строит дерево, размещая узлы в определённом порядке и устанавливая между ними связи.
Построенное дерево хорошо для декодирования файла. Но для кодирования файла оно неудобно, потому что неизвестно, в каком направлении следует идти от корня, чтобы добраться до необходимого символа. Для этого удобнее построить таблицу преобразования символов в код. Поэтому определим ещё одну структуру:

// Описатель кодового символа

Здесь opcode ― кодовая комбинация символа, а len — её длина (в битах). И объявим таблицу из 256 таких структур:

Зная кодируемый символ, можно определить его кодовое слово по таблице. Теперь перейдём непосредственно к подсчёту частот символов (и не только).
Подсчёт частот символов
В принципе, это действие не составляет труда. Достаточно открыть файл и подсчитать в нём число символов, заполнив соответствующие структуры. Посмотрим реализацию этого действия.
Для этого объявим глобальные дескрипторы файлов:

in ― файл, из которого осуществляется чтение несжатых данных.
out ― файл, в который осуществляется запись сжатых данных.
assemb ― файл, в который будет сохранено дерево в удобном для распаковки виде. Так как распаковщик будет написан на ассемблере, то вполне рационально дерево сделать частью распаковщика, то есть представить его в виде инструкций на Ассемблере.
Первым делом необходимо проинициализировать все структуры нулевыми значениями:

// Подсчёт частот символов

int i; // переменная цикла

int count=0; // вторая переменная цикла

DWORD TotalCount=0; // размер файла.

// Инициализация структур

После этого мы подсчитываем число вхождений символа в файл и размер файла (конечно, не самым идеальным способом, но в примере нужна наглядность):

// Подсчёт частот символов (по-символьно)

while (!feof(in)) // пока не достигнут конец файла

if (i!=EOF) // если не конец файла

Freq[i].freq++; // частота ++

TotalCount++; // размер ++

Так как код неравномерный, то распаковщику будет проблематично узнать число считываемых символов. Поэтому в таблице распаковки необходимо зафиксировать его размер:

// «Сообщаем» распаковщику размер файла

fprintf(assemb, «coded_file_size:n dd %8lxhnn«, TotalCount);

После этого все используемые символы смещаются в начало массива, а неиспользуемые затираются (путём перестановок).

// смещаем все неиспользуемые символы в конец

while (i<count) // пока не достигли конца

if (Freq[i].freq==0) // если частота 0

Freq[i]=Freq[—count]; // то копируем запись из конца

i++; // всё ОК — двигаемся дальше.

И только после такой «сортировки» выделяется память под узлы (для некоторой экономии).

// Выделяем память под узлы

Freq[i].table=new TTable; // создаём узел

Freq[i].table—>left=0; // без соединений

Freq[i].table—>right=0; // без соединений

Freq[i].table—>ch=Freq.ch; // копируем символ

Freq[i].freq=Freq.freq; // и частоту

Таким образом, мы написали функцию первоначальной иницализации системы, или, если смотреть на алгоритм в первой части статьи, «записали используемые символы в столбик и приписали к ним вероятности», а также для каждого символа создали «отправную точку» ― узел ― и проинициализировали её. В поля left и right записали нули. Таким образом, если узел будет в дереве последним, то это будет легко увидеть по left и right, равным нулю.
Создание дерева
Итак, в предыдущем разделе мы «записали используемые символы в столбик и приписали к ним вероятности». На самом деле, мы приписали к ним не вероятности, а числители дроби (то есть количество вхождений символов в файл). Теперь надо построить дерево. Но для того, чтобы это сделать, необходимо найти минимальный элемент в списке. Для этого вводим функцию, в которую передаём два параметра ― количество элементов в списке и элемент, который следует исключить (потому что искать будем парами, и будет очень неприятно, если мы от функции дважды получим один и тот же элемент):

// поиск узла с наименьшей вероятностью.

int FindLeast(int count, int index)

DWORD min=(index==0) ? 1 : 0; // элемент, который считаем

for (i=1; i<count; i++) // цикл по массиву

if (i!=index) // если элемент не исключён

if (Freq[i].freq<Freq[min].freq) // сравниваем

min=i; // меньше минимума — запоминаем

return min; // возвращаем индекс минимума

Поиск реализован несложно: сначала выбираем «минимальный» элемент массива. Если исключаемый элемент ― 0, то берём в качестве минимума первый элемент, в противном случае минимумом считаем нулевой. По мере прохождения по массиву сравниваем текущий элемент с «минимальным», и если он окажется меньше, то его помечаем как минимальный.
Теперь, собственно говоря, сама функция построения дерева:

// Функция построения дерева

int ind1, ind2; // индексы элементов

TTable *table; // указатель на «новый узел»

while (count>1) // цикл, пока не достигли корня

ind1=FindLeast(count,—1); // первый узел

ind2=FindLeast(count,ind1); // второй узел

table=new TTable; // создаём новый узел

table—>ch=—1; // не конечный

table—>left=Freq[ind1].table; // 0 — узел 1

table—>right=Freq[ind2].table; // 1 — узел 2

Freq[ind1].ch=—1; // модифицируем запись о

Freq[ind1].freq+=Freq[ind2].freq; // частоте для символа

Freq[ind1].table=table; // и пишем новый узел

if (ind2!=(—count)) // если ind2 не последний

Freq[ind2]=Freq[count]; // то на его место

// помещаем последний в массиве

Таблица кодовых символов
Итак, дерево в памяти мы построили: попарно брали два узла, создавали новый узел, в который записывали на них указатели, после чего второй узел удаляли из списка, а вместо первого узла писали новый с разветвлением.
Теперь возникает ещё одна проблема: кодировать по дереву неудобно, потому что необходимо точно знать, по какому пути находится тот или иной символ. Однако проблема решается довольно просто: создаётся ещё одна таблица ― таблица кодовых символов ― в неё и записываются битовые комбинации всех используемых символов. Для этого достаточно однократно рекурсивно обойти дерево. Заодно, чтобы повторно его не обходить, можно в функцию обхода добавить генерацию ассемблерного файла для дальнейшего декодирования сжатых данных (см. раздел «Проектирование«).
Собственно, сама функция не сложна. Она должна приписывать к кодовой комбинации 0 или 1, если узел не конечный, в противном случае добавить кодовый символ в таблицу. Помимо всего этого, сгенерировать ассемблерный файл. Рассмотрим эту функцию:

// Функция рекурсивного обхода дерева

void RecurseMake(TTable *tbl, DWORD opcode, int len)

fprintf(assemb,«opcode%08lx_%04x:n«,opcode,len); // метку в файл

if (tbl—>ch!=—1) // узел конечный

Opcodes[tbl—>ch].opcode=(opcode>>mod); // сохраняем код

Opcodes[tbl—>ch].len=len; // и его длину (в битах)

// и создаём соответствующую метку

fprintf(assemb,» db %03xh,0ffh,0ffh,0ffhnn«,tbl—>ch);

opcode>>=1; // освобождаем место под новый бит

len++; // увеличиваем длину кодового слова

// делаем ссылки на метки символов

fprintf(assemb,» dw opcode%08lx_%04xn«,opcode,len);

fprintf(assemb,» dw opcode%08lx_%04xnn«,opcode|0x80000000,len);

RecurseMake(tbl—>left,opcode,len);

RecurseMake(tbl—>right,opcode|0x80000000,len);

// удаляем узел (он уже не нужен)

Помимо всего прочего, после прохождения узла функция удаляет его (освобождает указатель). Теперь разберёмся, что за параметры передаются в функцию.

tbl ― узел, который надо обойти.

opcode ― текущее кодовое слово. Старший бит должен быть всегда свободен.

len ― длина кодового слова.

В принципе, функция не сложнее «классического факториала» и не должна вызывать трудностей.
Битовый вывод
Вот мы и добрались до не самой приятной части нашего архиватора, а именно ― до вывода кодовых символов в файл. Проблема состоит в том, что кодовые символы имеют неравномерную длину и вывод приходится осуществлять побитовый. В этом поможет функция PutCode. Но для начала объявим две переменные ― счётчик битов в байте и выводимый байт:

OutBits увеличивается на один при каждом выводе бита, OutBits==8 сигнализирует о том, что OutChar следует сохранить в файл.

// получаем длину кодового слова и само кодовое слово

outcode=Opcodes[ch].opcode; // кодовое слово

len=Opcodes[ch].len; // длина (в битах)

while (len>0) // выводим по-битно

// Цикл пока переменная OutBits занята не полностью

while ((OutBits<8) && (len>0))

OutChar>>=1; // освобождаем место

OutChar|=((outcode&1)<<7); // и в него помещаем бит

outcode>>=1; // следующий бит кода

len—; // уменьшаем длину

OutBits++; // количество битов выросло

// если используются все 8 бит, то сохраняем их в файл

fputc(OutChar,out); // сохраняем в файл

Помимо этого, нужно организовать что-то вроде «fflush», то есть после вывода последнего кодового слова OutChar не поместится в выходной файл, так как OutBits!=8. Отсюда появляется ещё одна небольшая функция:

// «Очистка» буфера битов

// Если в буфере есть биты

OutChar>>=8—OutBits; // сдвигаем

fputc(OutChar,out); // и сохраняем в файле

Вызываем помощников
Все рассмотренные ранее функции не являются основными. Но с их помощью можно проиллюстрировать простой порядок действий:
1. Выписать все элементы в столбик и приписать вероятности.
2. Построить дерево по полученному столбику.
3. Записать кодовую таблицу символов.
4. По кодовой таблице закодировать исходные данные.
Собственно говоря, вот и функция, которая выполняет эти действия:

// Создание сжатого файла

// выписать все элементы в столбик и приписать вероятности

// записать кодовую таблицу символов

RecurseMake(Freq[0].table,0,0);

// закодировать по кодовой таблице исходные данные

while ((ch=fgetc(in))!=EOF)

EndPut(); // «очистить буфер»

Мейн
Всё, все функции готовы. Осталось только реализовать функцию main. Необходимо определить, какие она должна получить аргументы. А всё очень просто ― имя исходного файла, имя закодированного файла, а также имя файла, в который будет помещена таблица. Лично я всю операцию по открытию/закрытию файлов решил возложить на main. И вот как это выглядит:

// Определение типов данных

typedef unsigned char BYTE;

typedef unsigned int WORD;

typedef unsigned long DWORD;

typedef unsigned char BYTE;

typedef unsigned short WORD;

typedef unsigned int DWORD;

// Ахтунг! Главная функция!

void main(int argc, char *argv[])

// поочереди открываем/закрываем файлы

if ((in=fopen(argv[1],«rb+»))!=0)

if ((out=fopen(argv[2],«wb+»))!=0)

if ((assemb=fopen(argv[3],«wb+»))!=0)

// дошли до момента, когда можно делать код

printf(«Compressed successfuln«);

printf(«Can’t open assembler table file %sn«,

printf(«Can’t create file %sn«,argv[2]);

printf(«Can’t open file %sn«,argv[1]);

printf(«Usage: XARCH source output asm-file»);

Постскриптум
Вот и эта статья подошла к своему логическому завершению. В принципе, здесь представлен вполне рабочий код. Однако стоит заметить, что этот код не всегда способен работать. Например, если частоты символов обладают следующей закономерностью: 0.5, 0.25, 0.125, 0.0625, то есть у каждого символа вероятность его появления обратнопропорциональна степени двойки. В таком случае максимальная длина символа составит 255 бит, что никак не поместится в переменную типа DWORD. Поэтому для таких особых случаев придётся немного поднапрячься и усложнить генерацию кодовой таблицы.
Да, чуть не забыл. Провёл бенчмарк, сжав эту статью. Получил отношение 1:1.41, что довольно-таки неплохо.
P.P.S.
Позволю себе немного пофилософствовать. Сначала я не знал C++ и говорил: «C++ это — язык программирования». Потом, когда стал его изучать, я всячески его хвалил: «он может то, может это, а вот это — вообще класс, это супер язык». Но помере набора опыта С++ стал для меня «просто языком программирования». Почувствуйте разницу между этими тремя утверждениями.
Скачать исходный код к статье

i	b_i	L_i(b_i)
1	011111	6
2	1	1
3	0110	4
4	011110	6
5	010	3
6	00	2
7	01110	5

Данные	1	2	6	7	2	2	6	2	Длина кода
Исходные	001	010	110	111	010	010	110	010	24 бит
Кодированные	011111	1	00	01110	1	1	00	1	19 бит

Данные	001101100001110001000111111	Длина кода
Кодированные	00	1	1	0110	00	01110	00	1	00	011111	1	27 бит
Исходные	6	2	2	3	6	7	6	2	6	1	2	33 бит

SadKo
Владимир Садовников

Регистрация:: 4 июн 2007

Публикаций:: 8

Joint Source-Channel Coding and Decoding

Michel Kieffer, Pierre Duhamel, in Academic Press Library in Mobile and Wireless Communications, 2014

Joint source-channel variable-length codes

JSC-VLC construction methods can be categorized according to the way prefix, suffix, and distance properties, average codeword length, etc., enter the process. On one extreme are methods that guarantee some properties at each step of the construction. At the other extreme, one considers an exhaustive list of codebooks, whose properties are examined to find the best one.

Bidirectional or Reversible Variable-Length Codes (RVLCs), introduced in [57], are instantaneously decodable both in the forward and backward directions (they satisfy the fix-free condition). RVLC design generally aims to minimize the average codeword length, see, e.g., [188,187,114,181,211,117,88], usually without accounting for constraints on the free distance.

Several extensions of the design techniques for RVLCs to the construction of VLCs with larger free distance have been considered. A simple extension of [187] to VLCs with free distance greater than or equal to 2 is given in [113,117]. This is done by imposing a minimum distance between codewords of the same length. In [184], the synthesis of even-weight VLCs is considered. This guarantees minimum distance 2 or more between sequences of codewords.

Two techniques for building JSC-VLCs with a free distance larger than 2 have been proposed in [30,17]. The first starts with a channel code, whose codewords are shortened while preserving some distance property. The second progressively builds codewords ensuring some diverging distance, i.e., the distance between prefixes, which lower bounds the distance between codewords. These techniques were improved in terms of complexity by Lamy and Paccaut [110] and Wang et al. [211]. In [130], a genetic algorithm-based code design is proposed, which maximizes the compression efficiency while satisfying a lower bound on the free distance. This approach complements the free distance lower bound in [30,17] with a real-valued correction term involving a dissimilarity measure of codewords limiting the free distance bound and the codeword occurrence probability. The SAT-based approach proposed in [171,6] may also incorporate constraints on the diverging, converging, and block distances of codewords. This allows to obtain codes with the requested distance property (the lower bound is guaranteed to be satisfied), but not necessarily the code with the optimum coding efficiency. The code optimization process is formulated as a mixed integer linear programming problem in [80]. A fixed code redundancy is considered. The constraint on the free distance of the code is formulated using [50].

For a given redundancy, a branch-and-prune search algorithm is proposed in [51] to find the VLC with largest free distance. The search criterion is the exact free distance (instead of a lower bound), which may be evaluated for JSC-VLCs using the techniques presented in [50]. For more efficient branch pruning in the proposed search algorithm, several free distance bounds for VLCs are introduced.

In [200], the search tree proposed by Huang et al. [88] is used in conjunction with the exact free distance evaluation technique proposed in [50] to build the VLC of minimum redundancy satisfying some free distance constraint. Several heuristics are provided to limit the search complexity.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123964991000121

Information Theory

Ali Grami, in Introduction to Digital Communications, 2016

9.3 Source Coding Theorem

Source coding, as shown in Figure 9.4, is a process by which the output of a DMS is converted into a sequence of bits, while meeting the requirement of being uniquely decodable. The objective is to minimize the average number of bits per source symbol by reducing the redundancy of the information source. Assuming the binary codeword assigned to the symbol m_i, with the probability p_i, has length l_i bits, and the number of source symbols is K, the average codeword length of the source encoder is then defined as follows:

Figure 9.4. Source encoding.

(9.10)L¯=∑i=1Kpili

Let L_min denote the minimum possible value of the average codeword length L¯. We then define the code efficiency η of the source encoder as follows:

(9.11)η=LminL¯≤1

For a very efficient code, we have η→1. The fundamental question is how to determine L_min. Shannon’s source coding theorem can provide the answer to this question. This theorem may be stated as follows: For a DMS of entropy H(X), the average codeword length L¯ for any distortionless source encoding is bounded as follows:

(9.12)HX≤L¯

Accordingly, the entropy H(X) of a DMS provides a fundamental limit on the average number of bits per source symbol, furthermore L¯ can be made as close to H(X) as desired for some suitably chosen code. This theorem only gives the necessary and sufficient condition for the existence of source codes. However, it fails to provide an algorithm for the design of source codes that can realize the performance predicted by this theorem. Note that with Lmin=HX, we may write the code efficiency as follows:

(9.13)η=HXL¯≤1

The source entropy provides a limit at which the source output can be compressed, where above the source entropy, it is possible to design such a source code, and below it, no source code can exist. Given a DMS of entropy H(X), the average codeword length L¯ of a prefix-free code is bounded as follows:

(9.14)HX≤L¯<HX+1

Furthermore, the equality is satisfied if and only if each symbol probability is an integer power of 12. If blocks of n bits are encoded, that is we employ n^th-order extension codes, the average codeword length of the extended code L¯n is then as follows:

(9.15)HX≤L¯n<HX+1n

For n=1, (9.15) becomes (9.14). It is important to highlight the fact that when n→∞, we get L¯n→HX, as desired. In other words, in a DMS, by increasing the encoding/decoding complexity caused by the large number of source symbols in the extension code, the average codeword length can be reduced to approach the source entropy.

Example 9.7

A source emits five equally-likely symbols x₁, x₂, x₃, x₄, and x₅, that is we have Px1=Px2=Px3=Px4=Px5=0.2. Find the source entropy H(x). Find fixed-length codes when n=1, n=2, and n=3. Determine the average number of bits for each case, and comment on the results.

Solution

Figure 9.5 shows the codewords for all three codes. Using (9.4), we calculate the source entropy, we thus have HX=5−0.2log20.2≌2.322 bits.

Figure 9.5. Extension codes for Example 9.7: (a) n=1 and 5 codewords, (b) n=2 and 25 codewords, and (c) n=3 and 125 codewords.

For n=1, each codeword has three bits and there are five codewords, each with a probability of 0.2=0.21. The average codeword length when n=1 is thus as follows: L¯1=3×5×0.2=3 bits.

For n=2, each codeword has five bits and there are 25 codewords, each with a probability of 0.04=0.22. The average codeword length when n=2 is thus as follows: L¯2=5×25×0.04=5 bits. However, for n=2, each 5-bit codeword represents two symbols, we therefore have on average 2.5=52 bits representing a symbol.

For n=3, each codeword has seven bits, there are 125 codewords and each with a probability of 0.008=0.23. The average codeword length when n=3 is thus as follows: L¯3=7×125×0.008=7 bits. However, for n=3, each 7-bit codeword represents three symbols, we therefore have on average 2.333≅73 bits representing a symbol.

We can thus conclude, as the source coding theorem indicates, that as n increases, the average codeword length approaches the source entropy, as reflected below:

L¯1=3>L¯2=2.5>L¯3=2.333>Hx=2.322

For n=3, the average codeword length is already almost equal to the source entropy. Thus, there is no need to employ an extension code with n=4, especially as n is increased, the code complexity is significantly increased.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780124076822000090

Lossless compression methods

David R. Bull, Fan Zhang, in Intelligent Image and Video Compression (Second Edition), 2021

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

A generic model for lossless encoding is shown in Fig. 7.2. This comprises a means of mapping the input symbols from the source into codewords. In order to provide compression, the symbol to codeword mapper must be conditioned by a representative probability model. A probability model can be derived directly from the input data being processed, from a priori assumptions, or from a combination of both. It is important to note that compression is not guaranteed – if the probability model is inaccurate, then no compression or even data expansion may result. As discussed in Chapter 3, the ideal symbol-to-code mapper will produce a codeword requiring log2⁡(1Pi) bits.

Figure 7.2. Generic model of lossless coding.

7.2.2 Entropy, efficiency, and redundancy

As described in Chapter 3, H is known as the source entropy, and represents the minimum number of bits per symbol required to code the signal. For a given encoder which codes a signal at an average rate (i.e., an average codeword length) l‾, the coding efficiency can be defined as

(7.1)E=Hl‾.

Thus, if we code a source in the most efficient manner and the code is unambiguous (uniquely decodable), then the rate of the code will equal its entropy.

A coding scheme can also be characterized by its redundancy, R:

(7.2)R=l‾−HH⋅100%.

7.2.3 Prefix codes and unique decodability

We noted earlier that Morse code needs spaces to delineate between its variable-length codewords. In modern digital compression systems we cannot afford to introduce a special codeword for “space,” as it creates overhead. The way we overcome this is to use what are referred to as prefix codes. These have the property of ensuring that no codeword is the prefix of any other, and hence (in the absence of errors) that each codeword is uniquely decodable. Consider the alternative codes for the four-letter alphabet {a1,a2,a3,a4} in Table 7.1.

Table 7.1. Alternative codes for a given probability distribution.

Letter	Probability	C₁	C₂	C₃
a1	0.5	0	0	0
a2	0.25	0	1	10
a3	0.125	1	00	110
a4	0.125	10	11	111
Av. length	1.125	1.25	1.75

Let us examine the three codes in this table. We can see that, in the case of C₁, there is ambiguity as a2a3=a1a3. Similarly for C₂, a1a1=a3. In fact, only C₃ is uniquely decodable and this is because it is a prefix code, i.e., no codeword is formed by a combination of other codewords. Because of this, it is self-synchronizing – a very useful property. The question is, how do we design self-synchronizing codes for larger alphabets? This is addressed in the next section.

Example 7.2

Coding redundancy

Consider a set of symbols with associated probabilities and codewords as given in the table below. Calculate the first order entropy of the alphabet and the redundancy of the encoding.

Symbol	Probability	Codeword
s0	0.06	0110
s1	0.23	10
s2	0.30	00
s3	0.15	010
s4	0.08	111
s5	0.06	0111
s6	0.06	1100
s7	0.06	1101

Solution

1. Average codeword length

The table is repeated below, including the average length of each codeword. The average length l‾ in this case is 2.71 bits/symbol.

Symbol	Prob.	Code	Av. length
s0	0.06	0110	0.24
s1	0.23	10	0.46
s2	0.30	00	0.60
s3	0.15	010	0.45
s4	0.08	111	0.24
s5	0.06	0111	0.24
s6	0.06	1100	0.24
s7	0.06	1101	0.24
Overall average length	2.71

2. First order entropy

The first order entropy for this alphabet is given by

H=−∑Plog2⁡P=−(0.06×log2⁡0.06+0.023×log2⁡0.23+0.3×log2⁡0.3+…+0.06×log2⁡0.06)=2.6849bits/symbol.

3. Redundancy

The redundancy of this encoding is

R=l‾−HH×100=2.71−2.68492.6849≈1%.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128203538000165

Lossless Compression Methods

David R. Bull, in Communicating Pictures, 2014

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

A generic model for lossless encoding is shown in Figure 7.2. This comprises a means of mapping the input symbols from the source into codewords. In order to provide compression, the symbol to codeword mapper must be conditioned by a representative probability model. A probability model can be derived directly from the input data being processed, from a priori assumptions or from a combination of both. It is important to note that compression is not guaranteed—if the probability model is inaccurate then no compression or even data expansion may result. As discussed in Chapter 3, the ideal symbol to code mapper will produce a codeword requiring log2(1/Pi) bits.

Figure 7.2. Generic model of lossless coding.

7.2.2 Entropy, efficiency, and redundancy

As described in Chapter 3, H is known as the source entropy, and represents the minimum number of bits per symbol required to code the signal. For a given encoder which codes a signal at an average rate (i.e. an average codeword length) l‾, the coding efficiency can be defined as:

(7.1)E=Hl‾

Thus, if we code a source in the most efficient manner and the code is unambiguous (uniquely decodable) then the rate of the code will equal its entropy.

A coding scheme can also be characterized by its redundancy, R:

(7.2)R=l‾-HH·100%

7.2.3 Prefix codes and unique decodability

We noted earlier that Morse code needs spaces to delineate between its variable length codewords. In modern digital compression systems we cannot afford to introduce a special codeword for “space” as it creates overhead. The way we overcome this is to use what are referred to as prefix codes. These have the property of ensuring that no codeword is the prefix of any other, and hence (in the absence of errors) that each codeword is uniquely decodable. Consider the alternative codes for the four-letter alphabet {a1,a2,a3,a4} in Table 7.1.

Table 7.1. Alternative codes for a given probability distribution.

Letter	Probability	C₁	C₂	C₃
a1	0.5	0	0	0
a2	0.25	0	1	10
a3	0.125	1	00	110
a4	0.125	10	11	111

Average length	1.125	1.25	1.75

Let us examine the three codes in this table. We can see that, in the case of C₁, there is ambiguity as a2a3=a1a3. Similarly for C₂, a1a1=a3. In fact, only C₃ is uniquely decodable and this is because it is a prefix code, i.e. no codeword is formed by a combination of other codewords. Because of this, it is self-synchronizing—a very useful property. The question is, how do we design self-synchronizing codes for larger alphabets? This is addressed in the next section.

Example 7.2 Coding redundancy

Consider a set of symbols with associated probabilities and codewords as given in the table below. Calculate the first order entropy of the alphabet and the redundancy of the encoding.

Symbol	Probability	Codeword
s0	0.06	0110
s1	0.23	10
s2	0.3	00
s3	0.15	010
s4	0.08	111
s5	0.06	0111
s6	0.06	1100
s7	0.06	1101

Solution

1.

Average codeword length

The table is repeated below including the average length of each codeword. The average length l‾ in this case is 2.71 bits/symbol.

Symbol	Probability	Code	Average length
s0	0.06	0110	0.24
s1	0.23	10	0.46
s2	0.3	00	0.6
s3	0.15	010	0.45
s4	0.08	111	0.24
s5	0.06	0111	0.24
s6	0.06	1100	0.24
s7	0.06	1101	0.24

Overall average length	2.71

2.

First order entropy

The first order entropy for this alphabet is given by:

H=-∑Plog2P=-(0.06×log20.06+0.023×log20.23+0.3×log20.3+⋯+0.06×log20.06)=2.6849bits/symbol

3.

Redundancy

The redundancy of this encoding is:

R=l‾-HH×100=2.71-2.68492.6849≈1%

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780124059061000076

Digital Image Compression

John W. Woods, in Multidimensional Signal, Image, and Video Processing and Coding (Second Edition), 2012

Information Measure

Assume that a source has M messages to send to a remote location. We could say that the amount of information is M or we could use any monotonic increasing function of M to measure the information. Now consider two independent sources, the first one with M messages and the second one also with M messages. The total number of messages is now the square M². On the other hand, one feels intuitively that the amount of information has only doubled here. If we adopt a logarithmic measure of information, then the amounts of information in the two cases are log₂ M and 2log₂ M, respectively, consistent with a doubling of information.

In our seemingly digital world, we transmit bits and so may like to represent information in terms of bits. For M messages, we would need about log₂ M bits to represent them; for example, for M = 8, we represent each message with a symbol consisting of a binary string of 3 = log₂ 8 bits. These binary symbols would be sent over a channel, and then the receiver would perform the inverse transformation back to the message set, such that receiving the binary string 010, the receiver would output the message 3. More generally, if two independent sources had different message numbers, say M₁ and M₂, then their total or combined information would be, in terms of our logarithmic measure, log₂ M₁ + log₂ M₂, and information would be an additive quantity expressed in bits. This is essentially the information concept of Hartley [27] that existed prior to Shannon’s classic work [28], Claude Shannon being considered the father of information theory. We see some limitations in Hartley’s approach; for example, what if the two sources are not independent? Certainly in the extreme case where two sources are totally dependent, the combined and single information should be the same. In between, we would expect a good measure of combined information to increase as the dependence between two sources decreases, reaching the additive (double) value in the limit of total independence of the sources.

Message	Symbol	Message	Symbol
1	000	5	100
2	001	6	101
3	010	7	110
4	011	8	111

There is another problem with Hartley’s measure log₂ M, in that there is no reason to believe that it is the smallest number of bits necessary for a general source with M messages. In the interests of compression and efficiency, we want a measure of the least amount of bits necessary to represent or store a message source. Now, considering again just one source with M messages, Hartley’s information measure represents each message with the same number of bits log₂ M. If all the messages are equally likely, this is reasonable, but what if they are not? Let’s take the case of a source of M messages {m₁, m₂, … , m_M} with probabilities p₁, p₂, … , p_M satisfying p_i ≥ 0, for each i and ∑i=1Mpi=1. Again, our intuition tells us that improbable messages carry more information than probable ones. One could say that it is no news when it snows in Alaska! So some kind of increasing function of 1/p_i may be a good measure of information. Interestingly, in the case where all M messages are equally likely, we have 1/p_i = M, and thus we can match Hartley’s information measure with log₂(1/p_i) bits for each message.

Definition 9.A–1 Source Entropy

The overall average information or entropy of source X then becomes

H(X)≜∑i=1Mpilog1pi=E[log1p(X)].

The Shannon information measure source entropy was first presented in his classic paper [28], where he showed this entropy to be the unique measure satisfying some simple continuity and compound message properties like what we have just explored. We will take Shannon’s entropy as our information measure in this course.

We usually choose 2 as our logarithm base (i.e., log = log₂), and we speak of bits. However, other choices are sometimes used. For example, for four-value logic, it would be convenient to measure information using log₄, and we could speak of ‘quads.’ Sometimes for mathematical simplicity the logarithm base is chosen as e, giving natural logarithms (i.e., log = ln), and we speak of nats. Converting between two scales (e.g., nats and bits) is simple. Just use the relation log₂ x = ln x/ln 2. Then H in bits equals H in nats divided by ln 2 = 0.69315, or equivalently multiplied by log₂ e = 1.44267. Note that H in bits is larger than H in nats (by about 44%) because the base 2 is smaller than the base e.

Example 9.A–1 Discrete Message Source

Again, we take the case of a source of M messages {m₁, m₂, … , m_M} with probabilities p₁, p₂, … , p_M satisfying p_i ≥ 0, for each i and ∑i=1Mpi=1. In particular, we take M = 4 with probabilities as given in the following table:

Then the information per symbol becomes

− log p₁	− log p₂	− log p₃	− log p₄
1	2	3	3

and we can construct binary strings to represent the messages, called source codewords, using the tree structure in Figure 9.A–1.

Calculating the average codeword lengthl¯, we find for this example

l¯=12×1+14×2+18×3+18×3=1.75 bits

Note that the individual codeword lengths are equal to − logp_i, and so the average codeword length is equal to the entropy here. In the general case, this is not so. It only occurs here because this source is dyadic; that is, all individual probabilities are of the form p_i = 2^−k for some positive integer k.

Figure 9.A–1. A convienent tree structure to calculate binary codewords given message probabilities.

We note that Shannon’s entropy, here 1.75 bits, is less than Hartley’s information measure of 2 bits and that this efficiency is achieved in this simple example by the variable-length binary codewords shown. Here are some properties of entropy.

Lemma 1 Entropy

For any source (random variable) X, we have H(X) ≥ 0.

Proof

Consider a probability p. We know 0 ≤ p ≤ 1, and so log₂ p ≥ 0. Then H(X)=Elog1p≥0.

Entropy is a measure of uncertainty. Consider a random variable X taking on M fixed values. If one of the values has probability 1, then all the remaining M − 1 values have probability zero, and H = 1 log₂ 1 + 0 log₂ ∞ = 0 since we take 0 log₂ ∞ at its limiting value limk→∞1klog2k=0. In fact, the maximum value of the entropy occurs when all the probabilities are equal (i.e., pi=1M where H=∑i=1M1Mlog2M=log2M).). We have the following theorem.

Theorem 9.A–1 Bounds on Entropy

For a random variable taking on M discrete values, we have the following bounds on entropy:

0≤H(X)≤log2M,

where the upper bound occurs when all values are equally likely and the minimum value 0 occurs when any one of the M values has probability 1.

Proof

The upper limit follows since log is a concave function (i.e., ∑pilog1pi≤log∑pi1pi=logM).).

Given two random variables X and Y, we can define joint and conditional entropy, respectively, as

H(X,Y)=∑x,yp(x,y)log1p(x,y)andH(Y|X)=∑x,yp(x,y)log1p(y|x).

We then have the following theorem.

Theorem 9.A–2 Chain Rule for Entropy

For any two random variables X and Y, we have

H(X,Y)=H(X)+H(Y|X).

Proof

Result is immediate upon substitution of the various definitions and recalling the chain rule for probabilities, we have p(x, y) = p(x)p(y|x).

Now, when the random variables are independent, i.e., p(y|x) = p(y), we have H(X,Y) = H(X) + H(Y). Note that the chain rule can be extended to N random variables by repeated application, so we also have

H(X1,X2,…,XN)=H(X1)+H(X2|X1)+H(X3|X1,X2)+⋯,

and in the case where the X_i are jointly independent, this simplifies to H(X₁, X₂, … , X_N) = H(X₁) + H(X₂) + H(X₃) + ⋯⋅

A most important quantity in information theory is mutual information between random variables X and Y, defined as

I(X;Y)≜∑x,yp(x,y) logp(x,y)p(x)p(y).

We speak of the mutual information between X and Y since it easily follows that I(X;Y) = I(Y;X). Mutual information is related to entropy as

(9.A–1)I(X;Y)=H(X)−H(X|Y),

which follows immediately from the definitions and the fact that p(x,y)p(x)p(y)=p(x|y)p(x). In words, we say that the mutual information between X and Y is equal to the uncertainty (entropy) of X less the uncertainty that remains in X given that Y is known. Thus, if X is the input to a communications channel (link) and Y is its output, it seems that I(X;Y) might actually measure the amount of information carried by Y about X. In fact, the channel coding theorem actually proves this and shows that the channel capacity (suitably defined) can be obtained by maximizing the mutual information.

Theorem 9.A–3 Mutual Information and Entropy

0≤I(X;Y)≤H(X),H(X|Y)≤H(X).

Proof

By (9.A–1), both of these two equations will be true if we can show mutual information I(X;Y) ≥ 0, because entropy and hence conditional entropy are always nonnegative. To show that mutual information is always positive, we proceed as

I(X;Y)=∑x,yp(x,y) logp(x,y)p(x)p(y)=(log e)∑x,yp(x,y) lnp(x,y)p(x)p(y).

Now, since ln x ≤ x − 1 for x > 0, we can say that ln1x≥1−x there. Substituting x with p(x)p(y)p(x,y), we then obtain

∑x,yp(x,y)lnp(x,y)p(x)p(y)≥∑x,yp(x,y)[1−p(x)p(y)p(x,y)]=∑x,yp(x,y)−∑x,yp(x)p(y)=1−1=0,

as was to be shown.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123814203000096

Performance improvement methods

Shigeyuki Takano, in Thinking Machines, 2021

6.2.2.2 Side-effect on inference accuracy

Table 6.4 [129] shows the error rates under a fixed-point precision with different combinations of numerical representation on the inference and training. Under non-convergence at a 16-bit fixed-point used for training, a 16-bit numerical representation is insufficient for training because of the small fraction of gradient parameters used in the calculation. In addition, the need for floating-point precision for training is demonstrated, and a fixed-point precision for training increases the error. This result supports a mixed precision architecture.

Table 6.4. Impact of fixed-point computations on error rate [129].

Inference	Training	Error [%]
Floating-Point	Floating-Point	0.82
Fixed-Point (16 bits)	Floating-Point	0.83
Fixed-Point (32 bits)	Floating-Point	0.83
Fixed-Point (16 bits)	Fixed-Point (16 bits)	(no convergence)
Fixed-Point (16 bits)	Fixed-Point (32 bits)	0.91

Table 6.5 [179] shows the accuracy of the inference on several neural network models with different fixed-point precision levels ranging from 2-bit to 8-bit combinations of activations, and the parameters of the convolution layer and fully connected layer. A decrease in accuracy of the inference ranging from 0.1 to 2.3 points is shown. This is a serious problem of the quantization. It seems that a neural network model having a relatively lower complexity does not have an impact on the inference accuracy when changing to an architecture with a lower numerical precision.

Table 6.5. CNN models with fixed-point precision [179].

Neural Network Model	Layer Outputs [Bits]	Conv Params [Bits]	FC Params [Bits]	FP32 Baseline Accuracy [%]	Fixed-Point Accuracy [%]
LeNet (Exp1)	4	4	4	99.1	99.0 (98.7)
LeNet (Exp2)	4	2	2	99.1	98.8 (98.0)
Full CIFAR-10	8	8	8	81.7	81.4 (80.6)
SqueezeNet (top-1)	8	8	8	57.7	57.1 (55.2)
CaffeNet (top-1)	8	8	8	56.9	56.0 (55.8)
GoogLeNet (top-1)	8	8	8	68.9	66.6 (66.1)

Table 6.6 shows the inference accuracy for AlexNet with a combination of activation (A) and weight (W) [265]. The top-1 accuracy is decreased by a superfluous quantization, such as a 1-bit activation and weight. At lower than a 4-bit quantization, the accuracy of the inference is easily decreased. This indicates that more quantization on the weight rather than on the activation has a greater impact on the inference accuracy. This means that a quantization of the parameters should be careful applied to suppress errors in the inference, implying that the training needs a quantization error interpolation as a regularization term of the cost function.

Table 6.6. AlexNet top-1 validation accuracy [265].

	32b A	8b A	4b A	2b A	1b A [%]
32b W	57.2	54.3	54.4	52.7	–
8b W	–	54.5	53.2	51.5	–
4b W	–	54.2	54.4	52.4	–
2b W	57.5	50.2	50.5	51.3	–
1b W	56.8	–	–	–	44.2

Fig. 6.11 shows the accuracy against the average codeword length per network parameter after network quantization for a 32-layer ResNet [135]. A codeword is equivalent to the bit width for the parameter. By quantizing more aggressively, i.e., less than 7-bit, the accuracy of the inference decreases. In addition, an aggressive quantization for the activation rather than the parameters introduces more errors. Both with and without fine-tuning show that a Hessian-weighted k-means quantization method achieves the best accuracy for the observed network model. The fine-tuning can suppress the decrease in accuracy under a lower numerical precision.

Figure 6.11. Accuracy vs. average codeword length [135].

Fig. 6.12 shows an error with a floating-point, 2-bit direct quantization of all weights, and 2-bit direct quantization only on the weight groups “In-h1,” “In-h2,” and “In-h4,” on different network sizes [342]. A trend in which a large-scale network can achieve high accuracy is shown. This fact seems to indicate that quantization can be interpolated through deeper networking. The decrease in the accuracy of the inference can be recovered through fine-tuning. Obviously, a network model for a mission critical task cannot have a smaller numerical precision.

Figure 6.12. Sensitivity analysis of direct quantization [342].

Fig. 6.13 shows the effect of a dynamic fixed-point representation on permutation-invariant MNIST, MNIST, and CIFAR-10. Note that the final test errors are normalized, which means that they are divided by the single float test error of the dataset. Fig. 6.13(a) shows the test error rate along with how many bits (excluding the sign) are used for the propagation. It shows that 7-bits (plus the sign-bit) are sufficient for the test evaluations. Fig. 6.13(b) shows a case of parameters updating the weight, in which a dynamic fixed-point needs a relatively narrower bit-width than a traditional fixed-point, at just 11-bits (plus the sign-bit). This approach is also effective in a traditional fixed-point representation.

Figure 6.13. Test error on dynamic fixed-point representation [140].

Research was conducted regarding the inference accuracy of XNOR-Net with weight binarization and both weight and input binarization as the training curve on ImageNet (ILSVRC2012), as shown in Fig. 6.14. The results show that XNOR-Net outperforms a binary connect (BC) and BinaryNeuralNet (BNN), respectively. However, the authors did not compare models having a higher precision, such as a single precision floating-point.

Figure 6.14. Top inference accuracy with XNOR-Net [301].

To summarize, superfluous quantization introduces a remarkable decrease in the accuracy of the inference. We must consider not only a quantization method but also a decrease in the inference accuracy on a neural network model. We should consider which method is better for the targeted neural network model in the case of an embedded solution.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128182796000165

Источник

Неравномерное кодирование. Средняя длина кодирования

В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.

Показателем экономичности или эффективности неравномерного кода является не длина отдельных кодовых слов, а «средняя» их длина, определяемая равенством:

$L(S,c)=sum_{i=1}^{n}p_i*|c(a_i)|$

где c(a_i) — кодовое слово, которым закодировано сообщение a_i , а — его длина, p_i — вероятность сообщения a_i ,— общее число сообщений источника . Для краткости записи формул далее могут использоваться обозначения и . Заметим, что обозначение средней длины кодирования через L(S,c) подчеркивает тот факт, что эта величина зависит как от источника сообщений , так и от способа кодирования .

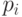
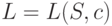
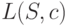
Наиболее экономным является код с наименьшей средней длиной 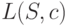L(S,c) . Сравним на примерах экономичность различных способов кодирования одного и того же источника.

Пусть источник содержит 4 сообщения с вероятностями . Эти сообщения можно закодировать кодовыми словами постоянной длины, состоящими из двух знаков, в алфавите в соответствии с кодовой таблицей.

Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.

В этой таблице, в отличие от предыдущей, наиболее частые сообщения A_1 и A_2 кодируются одним двоичным знаком. Для последнего варианта кодирования имеем

в то время как для равномерного кода средняя длина 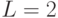L=2 (она совпадает с общей длиной кодовых слов). Из рассмотренного примера видно, что кодирование сообщений словами различной длины может дать суще-ственное (почти в два раза) увеличение экономичности кодирования.

При использовании неравномерных кодов появляется проблема, которую поясним на примере последней кодовой таблицы. Пусть при помощи этой таблицы кодируется последовательность сообщений , в результате чего она преобразуется в следующий двоичный текст: 010110. Первый знак исходного сообщения декодируется однозначно — это A_1 . Однако дальше начинается неопределенность: или . Это лишь некоторые из возможных вариантов декодирования исходной последовательности знаков.

Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.

Существо проблемы — в невозможности однозначного выделения кодовых слов. Для ее решения следовало бы отделить одно кодовое слово от другого. Разумеется, это можно сделать, но лишь используя либо паузу между словами, либо специальный разделительный знак, для которого необходимо особое кодовое обозначение. И тот, и другой путь, во-первых, противоречат описанному выше способу кодирования слов путем конкатенации кодов знаков a_i , образующих слово, и, во-вторых, приведет к значительному удлинению кодового текста, сводя на нет преимущества использования кодов переменной длины.

Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).

Рассмотрим код (схему алфавитного кодирования) , заданный кодовой таблицей

$a_1 to beta_1\ A_2 to beta_2\ vdots\ A_k to beta_k$

и различные слова, составленные из элементарных кодов.

Определение. Код называется однозначно декодируемым, если

$beta_{i_1}, beta_{i_2}, dots, beta_{i_k}=beta_{j_1}, beta_{j_2}, dots, beta_{i_m} Rightarrow k=m$

$forall_t=1,2, dots, k\ i_1=j_1$

то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды.

Если таблица кодов содержит одинаковые кодовые слова, то есть если

$exists_{i,j}, I ne j\ beta_i= beta_j$

то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.

Префиксные коды

Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].

Определение. Код, обладающий тем свойством, что никакое кодовое слово не является началом (префиксом) другого кодового слова, называется префиксным.

Теорема 1. Префиксный код является однозначно декодируемым.

Доказательство. Предположим противное. Тогда существует слово beta которое можно представить двумя разными способами $beta_i=beta_{i1} beta_{i2} dots beta_{ik}=beta_{j1} beta_{j2} dots beta_{jm}$ , причем до номера все подслова в обоих представлениях (разложениях) совпадают, а слова $beta_{i_t}$ и $beta_{j_t}$ различны. 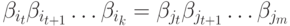Отбросив одинаковые префиксы двух равных слов (представлений), получим совпадающие окончания $beta_{i_t} beta_{i_{t+1}} dots beta_{i_k}=beta_{j_t} beta_{j_{t+1}} dots beta_{j_m}$ , начинающиеся с различных слов. Из-за равенства окончаний первые буквы слов $beta_{i_t}$ и $beta_{j_t}$ должны совпадать. По аналогичной причине должны совпадать и вторые буквы этих слов и т.д. Это означает, что неравенство слов $beta_{i_t}$ и $beta_{j_t}$ может заключаться только в том, что они имеют разную длину и, следовательно, одно из них является префиксом другого. Это противоречит префиксности кода.

Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.

На рис.6.5 а) — дерево, соответствующие коду, у которого все слова имеют одинаковую длину. Кружками помечены те вершины, которые соответствуют кодовым словам. В данном случае это 4 двухбуквенных слова, составляющих второй уровень словарного дерева (универсума). Нетрудно понять, как отражается свойство префиксности или его отсутствие на кодовом дереве. Рассмотрим код, состоящий из слов (0, 10, 111). Это не полный префиксный код, так как к коду можно добавить слово 110, которое получается из слова 11 приписыванием справа 0. Эта операция показана на рис.6.5 б) пунктирным ребром. На рис.6.5 в) показано дерево полного префиксного кода. В данном случае вершины, соответствующие словам префиксного кода, как бы «разрезают» словарный универсум на две части — «верхнюю» и «нижнюю». Если попытаться добавить слово «выше» кодовых слов, то одно из кодовых слов станет префиксом добавляемого слова. Если добавлять слово «ниже» слов префиксного кода, то добавляемое слово окажется префиксом одного из кодовых слов. В обоих случаях нарушается свойство префиксности. На рис.6.5 г) представлено дерево для рассмотренного ранее кода, не обладающего свойством префиксности. Таким образом, если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.

Рис.
6.5.
Деревья различных кодов

Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.

Пример. Код, состоящий из двоичных кодовых слов 1, 10, — не префиксный, но может быть однозначно декодирован. Появление символа 1 означает начало нового кодового слова. Последнее остается справедливым для кода, каждое слово которого есть единица с последующими нулями. Разумеется, подобные коды далеко не самые экономные.

Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.

Источник

Вторая часть перевода лонгрида посвященного визуализации концепций из теории информации. Во второй части рассматриваются энтропия, перекрестная энтропия, дивергенция Кульбака-Лейблера, взаимная информация и дробные биты. Все концепции снабжены прекрасными визуальными объяснениями.

Для полноты восприятия, перед чтением второй части, рекомендую ознакомиться с первой.

Вычисление энтропии

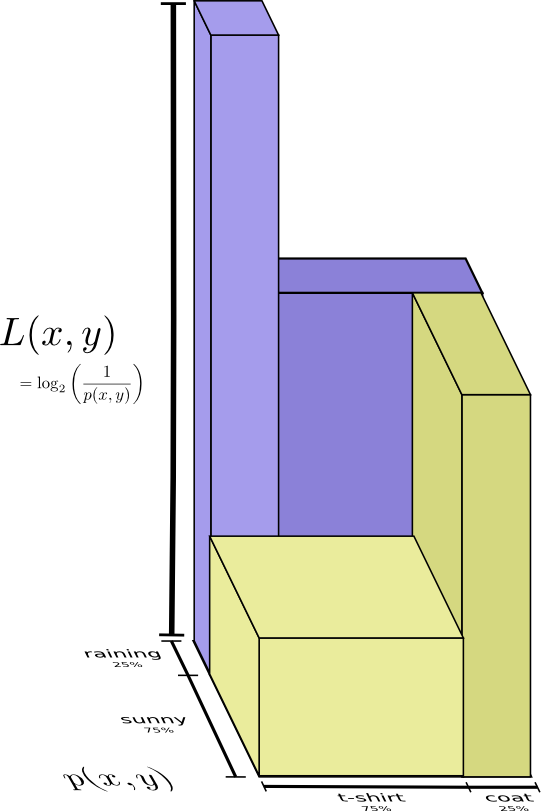
Напомним, что стоимость сообщения длиной

$L$ равна

$frac{1}{2^L}$ . мы можем инвертировать это значение, чтобы получить длину сообщения, которое стоит заданную сумму:

$log_2 (frac{1}{cost})$ . Поскольку мы тратим

$p(x)$ на кодовое слово для

$x$ , длина будет равна

$log_2(frac{1}{p(x)})$ . На рисунке выбор лучших длин кодовых слов.

Ранее мы обсуждали, что существует фундаментальный предел того, насколько коротким может быть среднее сообщение для передачи событий из определенного распределения вероятностей

$p$ . этот предел, средняя длина сообщения при использовании наилучшей системы кодирования, называется энтропией

. Теперь, когда мы знаем оптимальную длину кодовых слов, мы можем ее вычислить!

$H(p)=sum_xp(x)log_2Bigg(frac{1}{p(x)}Bigg)$

(Часто энтропию записывают как

используя равенство

. Мне кажется первая версия более интуитивна поэтому мы продолжим использовать ее.)

Если я хочу сообщить, какое событие произошло, то независимо от того, что я делаю, в среднем мне нужно отправить столько битов.

Среднее количество информации, необходимой для передачи чего-либо, имеет прямые следствия для сжатия. Но есть ли другие причины, по которым мы должны заботиться об этом? Да! Оно описывает мою неопределенность, и дает возможность количественно оценить информацию.

Если бы я знал наверняка, что произойдет, мне вообще не пришлось бы посылать сообщение! Если есть две вещи, которые могут произойти с вероятностью 50%, мне нужно отправить только 1 бит. Но если существует 64 различных события, которые могут произойти с одинаковой вероятностью, мне придется отправить 6 битов. Чем более концентрирована вероятность, тем больше у меня возможностей создать умный код с короткими средними сообщениями. Чем расплывчатее вероятность, тем длиннее должны быть мои сообщения.

Чем неопределеннее результат, тем больше я узнаю в среднем, когда мне сообщают о произошедшем.

Перекрестная энтропия

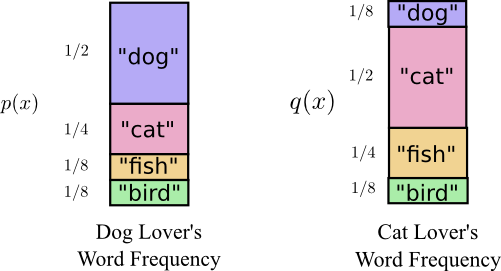
Незадолго до переезда в Австралию Боб женился на Алисе, тоже воображаемой. К моему удивлению, а также к удивлению других персонажей в моей голове, Алиса не была любительницей собак. Она была любительницей кошек. Несмотря на это, они смогли найти общий язык в своей общей одержимости животными и очень ограниченном словарном запасе.

Эти двое используют одни и те же слова, только с разной частотой. Боб все время говорит о собаках, Алиса все время говорит о кошках.

Сначала Алиса посылала мне сообщения, используя код Боба. К сожалению, ее сообщения были длиннее, чем требовалось. Код Боба был оптимизирован под его распределение вероятностей. У Алисы другое распределение вероятностей, и код для нее неоптимален. Средняя длина кодового слова, когда Боб использует свой код, составляет 1,75 бита, когда же его использует Алиса, то 2,25. Было бы еще хуже, если бы эти двое не были так похожи!

Средняя длина сообщения из одного распределения с оптимальным кодом другого распределения называется перекрестной энтропией. Формально мы можем определить перекрестную энтропию следующим образом:

$H_p(q)=sum_xq(x)log_2Bigg(frac{1}{p(x)}Bigg)$

В данном случае речь идет о перекрестной энтропии частоты слов кошатницы Алисы по отношению к частоте слов собачатника Боба.

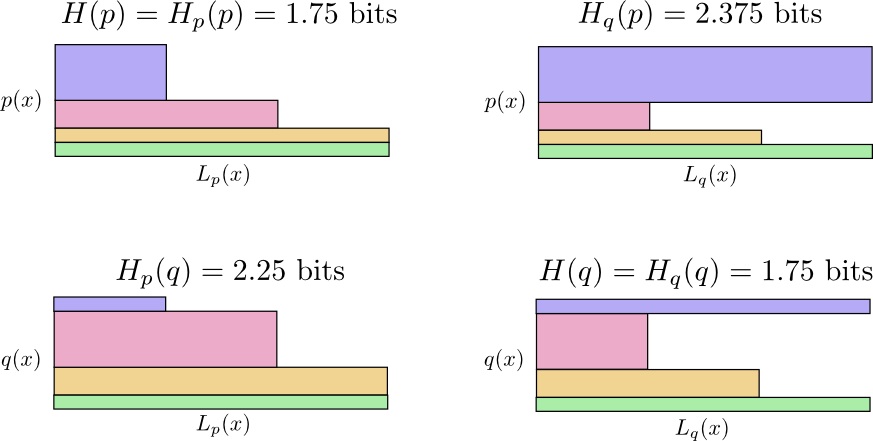
Чтобы снизить стоимость нашей связи, я попросил Алису использовать ее собственный код. К моему облегчению, это снизило ее среднюю длину сообщения. Но это создавало новую проблему: иногда Боб случайно использовал код Алисы. Удивительно, но хуже когда Боб использует код Алисы, чем когда Алиса используют код Боба!

Итак, теперь у нас есть четыре возможности:

Это не так интуитивно, как можно было бы подумать. Например, мы можем видеть, что

. Можем ли мы каким-то образом увидеть, как эти четыре значения соотносятся друг с другом?

На следующей диаграмме каждый подграфик представляет одну из этих 4 возможностей. Иллюстрации визуализируют среднюю длину сообщения. Они организованы в квадрат, так что, если сообщения из одного и того же распределения, диаграммы находятся рядом, а если они используют одни и те же коды, они находятся друг над другом. Это позволяет вам визуально совместить распределения и коды вместе.

Видите почему

такой большой, потому событие отмеченное синим цветом часто встречается при

$p$ , но получает длинное кодовое слово, потому что оно очень редко при

$q$ . С другой стороны, частые события при

$q$ менее распространены при

$p$ , но разница менее резкая, поэтому

немного меньше.

Перекрестная энтропия не является симметричной.

Так, почему вас должна волновать перекрестная энтропия? Перекрестная энтропия дает нам способ выразить, насколько различны два распределения вероятностей. Чем сильнее отличаются распределения

$p$ и

$q$ , тем больше перекрестная энтропия

$p$ относительно

$q$ будет больше энтропии

$p$ .

Аналогично, чем больше

$q$ отличается от

$p$ , тем больше перекрестная энтропия

$q$ относительно

$p$ будет больше энтропии

$q$ .

По-настоящему интересной вещью является разница между энтропией и перекрестной энтропией. Эта разница равна тому насколько длиннее наши сообщения, потому что мы использовали код, оптимизированный для другого распределения. Если распределения одинаковы, то эта разница будет равна нулю. По мере того как отличия увеличиваются, она будет становиться больше.

Мы называем это различие дивергенцией Кульбака-Лейблера, или просто KL-дивергенцией. KL-дивергенция

$p$ относительно

$q$ ,

определяется так:

Самое замечательное в KL-дивергенции то, что она похожа на расстояние между двумя распределениями. Он измеряет, насколько они разные! (Если вы примете эту идею всерьез, вы придете к информационной геометрии.)

Перекрестная энтропия и KL-дивергенция невероятно полезны в машинном обучении. Часто мы хотим, чтобы одно распределение было близко к другому. Например, мы можем хотеть, чтобы предсказанное распределение было близко к основной истине. KL-дивергенция дает нам естественный способ сделать это, и поэтому она проявляется всюду.

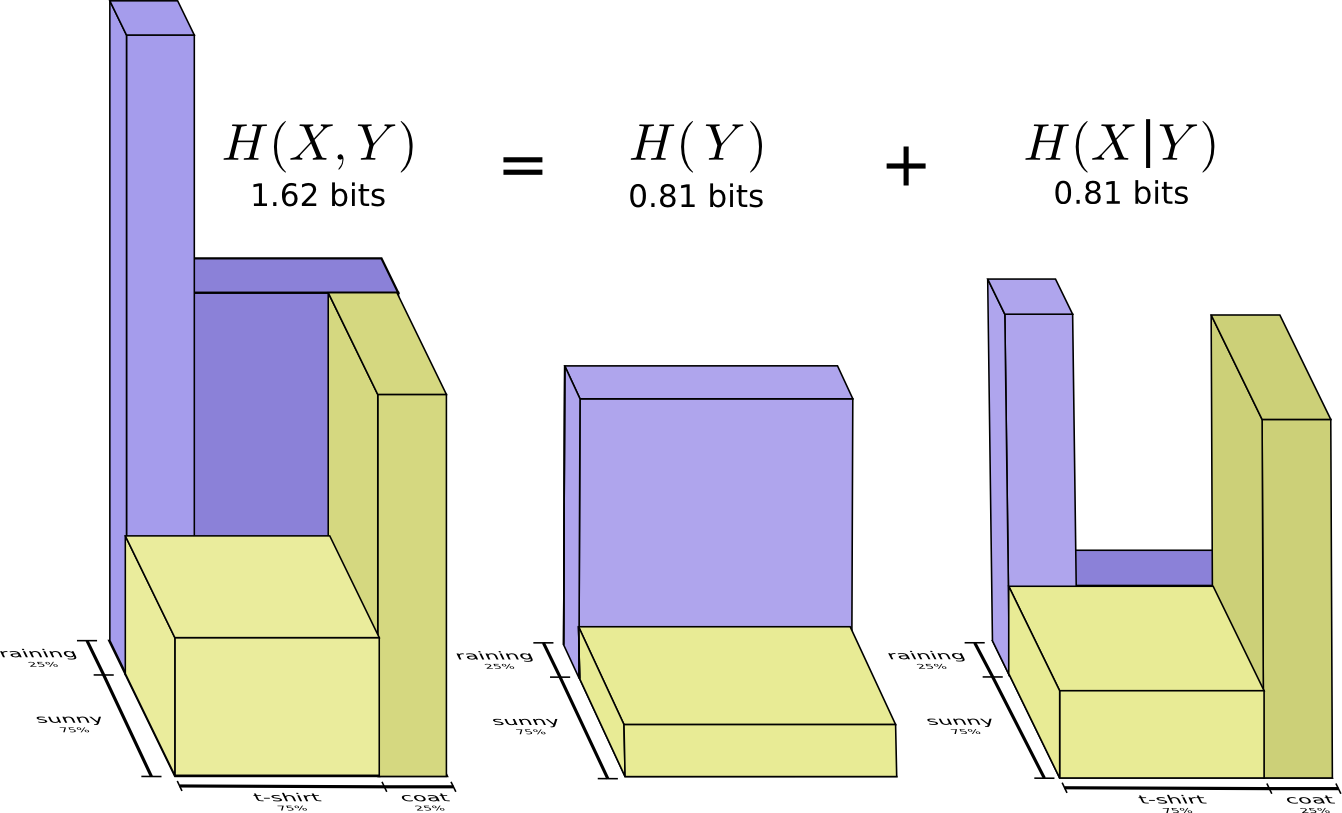
Энтропия и несколько переменных

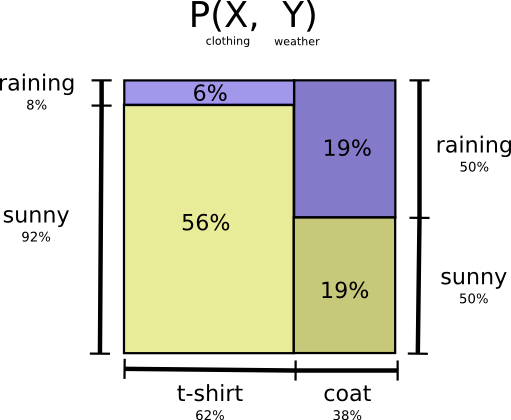
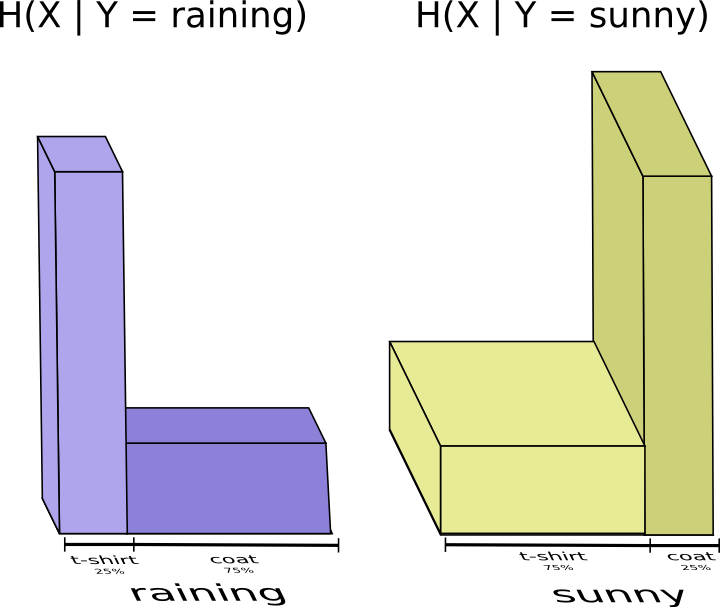
Давайте вернемся к нашему примеру с погодой и одеждой, приведенному ранее:

Моя мама, как и многие родители, иногда беспокоится, что я не одеваюсь соответственно погоде. (У нее есть веские основания для подозрений – я бывает не ношу плащ зимой.) Поэтому она часто хочет знать и погоду, и во что я одет. Сколько битов я должен послать ей, чтобы сообщить об этом?

Самый простой способ подумать об этом — выровнять распределение вероятностей:

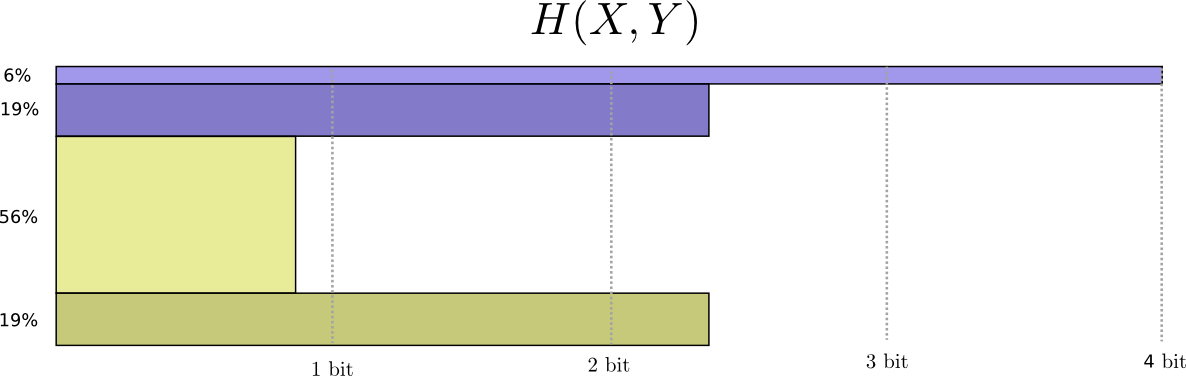
Теперь мы можем вычислить оптимальные кодовые слова для событий с такими вероятностями и вычислить среднюю длину сообщения:

Мы называем это совместной энтропией

$X$ и

$Y$ , определенной следующим образом:

$H(X,Y)=sum_{x,y}p(x,y)log_2bigg(frac{1}{p(x,y)}bigg)$

Оно совпадает с нашим обычным определением, за исключением двух переменных вместо одной.

Немного лучший образ этого, без выравнивания распределения получается если представить длину кодового слова в третьем измерении. Теперь энтропия — это объем!

Но предположим, что моя мама уже знает погоду. Она может посмотреть ее в новостях. Сколько тогда информации мне нужно предоставить?

Похоже, мне нужно отправить информации достаточно, чтобы сообщить какая одежда на мне надета. Но на самом деле мне нужно посылать меньше информации, потому что от погоды сильно зависит то, какую одежду я надену! Давайте рассмотрим случай с дождем и с солнцем отдельно.

В обоих случаях мне не нужно посылать слишком много информации в среднем, потому что погода дает мне хорошее предположение о том, каким будет правильный ответ. Когда солнце, я могу использовать специальный оптимизированный для солнца код, а когда идет дождь, я могу использовать оптимизированный для дождя код. В обоих случаях я посылаю меньше информации, чем если бы я использовал общий код для обоих. Чтобы получить среднее количество информации, которое мне нужно отправить моей матери, я просто сложил эти два случая вместе…

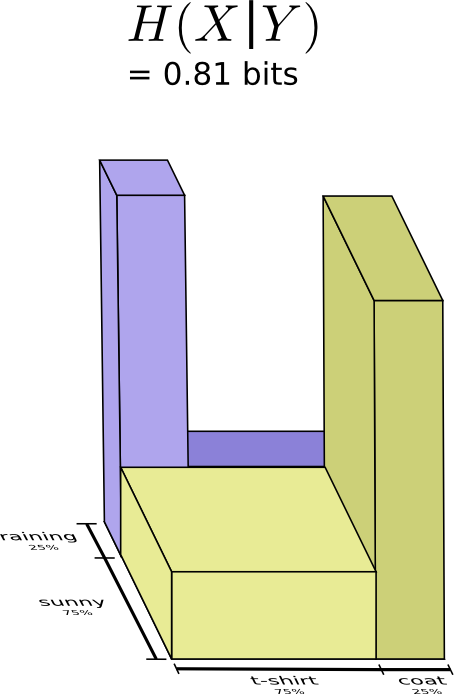
Мы называем это условной энтропией. Если вы формализуете его в уравнение, вы получаете:

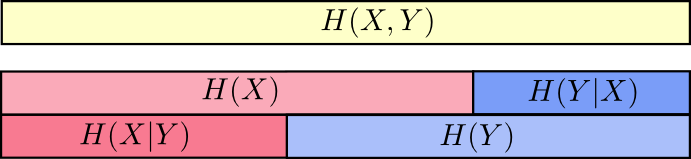
$H(X|Y)=sum_yp(y)sum_xp(x|y)log_2bigg(frac{1}{p(x|y)}bigg)$

$=sum_{x,y}p(x,y)log_2bigg(frac{1}{p(x|y)}bigg)$

Взаимная информация

В предыдущем разделе мы выяснили, что знание одной переменной может означать, что для сообщения значения другой переменной требуется передать меньше информации.

Хороший способ думать об этом — это представить себе количество информации в виде полос. Эти полосы перекрываются, если между ними есть общая информация. Например, некоторая часть информации в

$X$ и

$Y$ общая, поэтому

$H(X)$ и

$H(Y)$ являются перекрывающимися полосами. И поскольку

— это информация обеих переменных, то это объединение полос

$H(X)$ и

$H(Y)$ .

Когда мы думаем о вещах таким образом, многое становится проще увидеть.

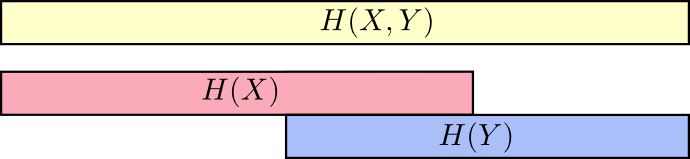
Например, мы уже отмечали, что для передачи информации как

$X$ , так и

$Y$ (“совместная энтропия”,

) требуется больше информации, чем для передачи только

$X$ (“предельная энтропия”,

$H(X)$ ). Но если вы уже знаете

$Y$ , то для передачи

$X$ (“условная энтропия”,

) требуется меньше информации, чем если бы вы этого не знали!

Это звучит сложновато, но если перевести на полосы то все оказывается очень просто.

— это информация, которую мы должны отправить, чтобы сообщить

$X$ тому, кто уже знает

$Y$ , информация в

$X$ , которая также не находится в

$Y$ . Визуально это означает, что

— это часть полосы

$H(X)$ , которая не перекрывается с

$H(Y)$ .

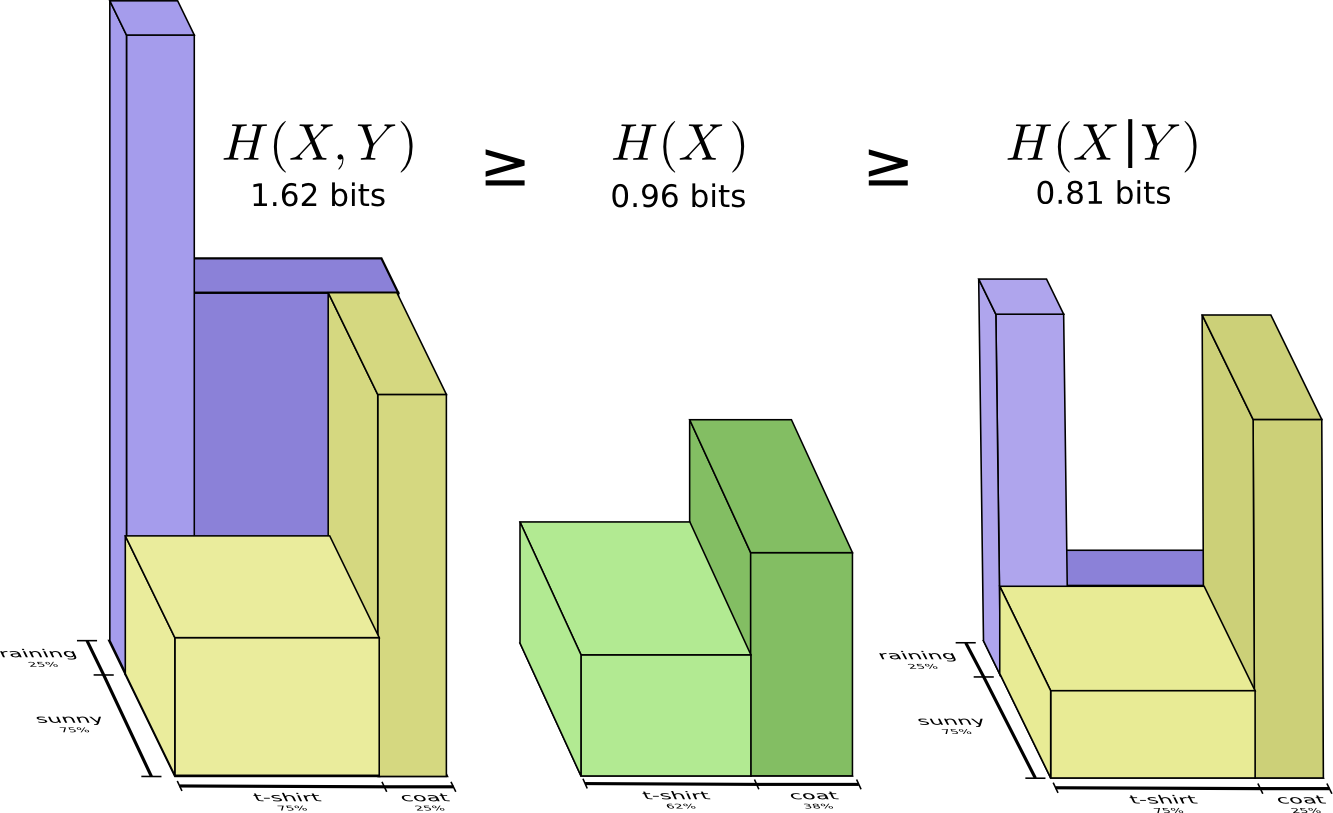
Теперь вы можете прочитать неравенство

прямо на следующей диаграмме.

Другое равенство следующее —

. Т.е. информация в

$X$ и

$Y$ это информация в

$Y$ плюс информация в

$X$ которой нет в

$Y$ .

Опять же, это трудно увидеть в уравнениях, но легко увидеть, если вы думаете в терминах перекрывающихся полос информации.

На этом этапе мы разбили информацию в

$X$ и

$Y$ несколькими способами. Мы знаем информацию в каждой переменной,

$H(X)$ и

$H(Y)$ . Мы знаем объединение информации в обоих

. У нас есть информация, которая находится в одной переменной, но отсутствует в другой,

. Многое из этого, вращается вокруг информации, общей в переменных — пересечения их информации. Мы называем это «взаимной информацией»,

, определяемой как:

Это определение верно, поскольку

содержит две копии взаимной информации, так как она находится и в

$X$ и в

$Y$ , в то время как

содержит только одну копию. (см. предыдущую диаграмму)

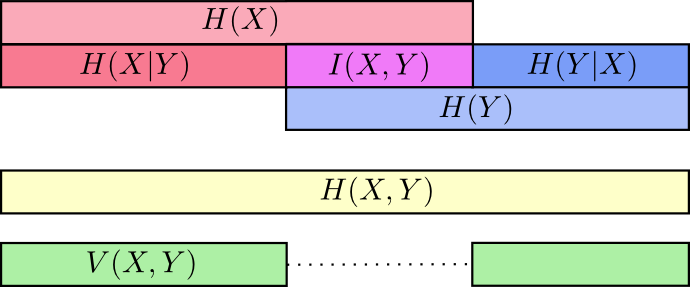
С взаимной информацией тесно связана вариация информации. Вариация информации — это информация, которая не является общей для переменных. Мы можем определить ее так:

Вариация информации интересна тем, что она дает нам метрику, понятие расстояния между различными переменными. Вариация информации между двумя переменными равна нулю, если знание значения одной переменной говорит вам о значении другой и становится больше по мере того, как они становятся более независимыми.

Как это соотносится с KL-дивергенцией, которая также дает нам понятие расстояния? KL-дивергенция это расстояние между двумя распределениями над одной и той же переменной или набору переменных. Напротив, вариация информации дает нам расстояние между двумя совместно распределенными переменными. KL дивергенция — это расхождение между распределениями, вариация информации внутри распределения.

Мы можем свести все это вместе в единую диаграмму, связывающую все эти различные виды информации:

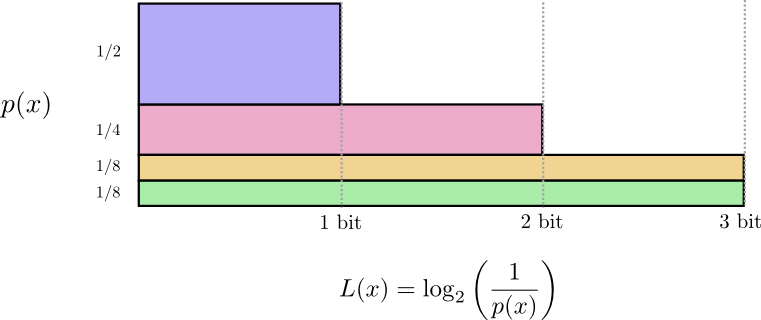
Дробные биты

Очень неинтуитивной вещью в теории информации является то, что мы можем иметь дробные количества битов. Это довольно странно. Что значит половина бита?

Вот простой ответ: часто нас интересует средняя длина сообщения, а не длина какого-либо конкретного сообщения. Если в половине случаев посылается один бит, а в половине случаев — два, то в среднем посылается полтора бита. Нет ничего странного в том, что средние величины могут быть дробными.

Но этим ответом мы уклоняемся от вопроса. Часто оптимальные длины кодовых слов тоже являются дробными. Что это значит?

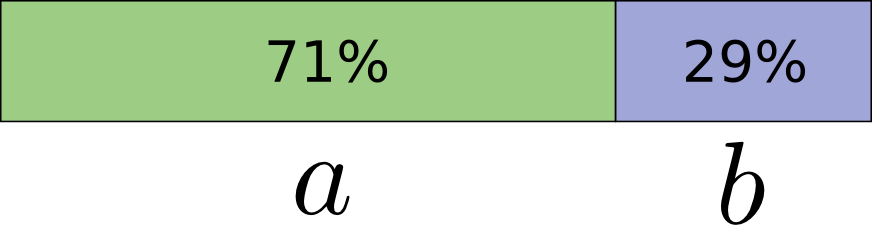
Чтобы быть конкретным, давайте рассмотрим распределение вероятностей, где одно событие,

$a$ , происходит 71% времени, а другое событие,

$b$ , происходит 29% времени.

Оптимальный код будет использовать 0,5 бит для представления

$a$ и 1,7 бита для представления

$b$ . Ну, если мы хотим отправить только одно из этих кодовых слов, такое представление невозможно. Мы вынуждены округлять до целого числа битов и отправлять в среднем 1 бит.

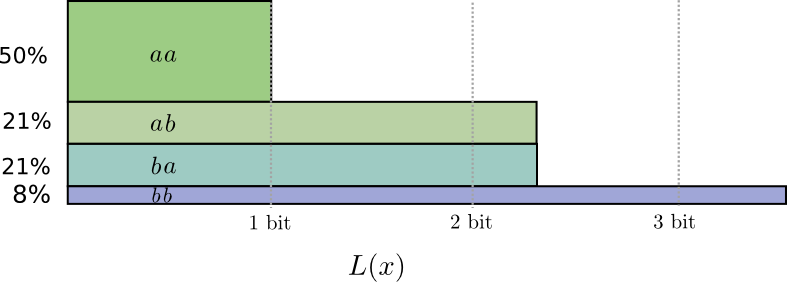
… Но если мы посылаем несколько сообщений одновременно, то оказывается можно сделать лучше. Давайте рассмотрим передачу двух событий из этого распределения. Если бы мы посылали их независимо, нам пришлось бы посылать два бита. Как нам это улучшить?

В половине случаев нам нужно посылать

$aa$ , в 21% случаев —

$ab$ или

$ba$ , а в 8% случаев —

$bb$ . Опять же, идеальный код включает дробные количества битов.

Если мы округлим длины кодовых слов, мы получим что-то вроде этого:

Эти коды дают нам среднюю длину сообщения 1,8 бит. Это меньше, чем 2 бита, когда мы посылаем сообщения независимо. Т.е. в этом случае мы посылаем 0,9 бит в среднем для каждого события. Если бы мы послали больше событий сразу, среднее значение стало бы еще меньше. При

$n$ стремящемся к бесконечности, накладные расходы, связанные с округлением нашего кода, исчезнут, и число битов на кодовое слово сойдется к энтропии.

Далее, обратите внимание, что идеальная длина кодового слова для события

$a$ составляла 0,5 бит, а идеальная длина для кодового слова

$aa$ — 1 бит. Идеальные длины кодовых слов складываются, даже если они дробные! Так что, если мы будем сообщать сразу несколько событий, длины будут складываться.

Как мы видим, существует реальный смысл, для дробные количеств битов информации, даже если фактические коды могут использовать только целые числа.

(На практике люди используют определенные схемы кодирования, которые эффективны в разных случаях. Код Хаффмана, который фактически является тем видом кода, который мы набросали здесь, не очень изящно обрабатывает дробные биты — вы должны группировать символы, как мы это делали выше, или использовать более сложные трюки, чтобы приблизиться к пределу энтропии. Арифметическое кодирование немного отличается, он элегантно обрабатывает дробные биты, чтобы быть асимптотически оптимальным.)

Заключение

Если нас волнует передача информации за минимальное количестве битов, то эти идеи, безусловно, фундаментальны. Если мы заботимся о сжатии данных, теория информации решает основные вопросы и дает нам фундаментально правильные абстракции. Но что, если нам все равно – разве это не экзотика?

Идеи из теории информации появляются во множестве контекстов: машинное обучение, квантовая физика, генетика, термодинамика и даже азартные игры. Практиков в этих областях теория информации заботит не потому, что они хотят сжать информацию. Их заботит то, что это имеет непреодолимую связь с их областью. Квантовую запутанность можно описать энтропией. Многие результаты в статистической механике и термодинамике можно получить, предположив максимальную энтропию о вещах, которых вы не знаете. Выигрыши и проигрыши игрока напрямую связаны с KL-дивергенцией в частности с итерационными сетапами (iterated setups).

Теория информации появляется во всех этих местах, потому что она предлагает конкретные, принципиальные формализации для многих вещей, которые мы должны выразить. Она дает нам способы измерения и выражения неопределенности, насколько различны два набора убеждений и что ответ на один вопрос говорит нам о других: насколько рассеяна вероятность, расстояние между распределениями вероятностей и насколько зависимы две переменные. Существуют ли альтернативные, подобные идеи? Конечно. Но идеи из теории информации чисты, они обладают действительно хорошими свойствами и основываются на принципах. В некоторых случаях эти идеи именно то, что вам нужно, а в других случаях они являются удобным посредником в хаотичном мире.

Машинное обучение — это то, что я знаю лучше всего, так что давайте поговорим об этом одну минуту. Очень распространенным видом задач в машинном обучении является классификация. Предположим, мы хотим посмотреть на картинку и предсказать, будет это изображение собаки или кошки. Наша модель может сказать что-то вроде: “есть 80% вероятности, что это изображение собаки, и 20% вероятности, что это кошка.» Допустим, правильный ответ — собака – насколько хорошо или плохо то, что мы сказали, что вероятность того что это собака 80%? Насколько лучше было бы сказать 85%?

Это важный вопрос, потому что нам нужно некоторое представление о том, насколько хороша или плоха наша модель, чтобы оптимизировать ее для достижения успеха. Что мы должны оптимизировать? Правильный ответ на самом деле зависит от того, для чего мы используем модель: заботимся ли мы только о том, была ли верна наша догадка, или нас волнует, насколько мы уверены в правильном ответе? Насколько это плохо — уверенно ошибаться? На это нет единственного правильного ответа. И часто невозможно узнать правильный ответ, потому что мы не знаем достаточно точно как будет использоваться модель, чтобы формализовать то, что нас в конечном счете волнует. Есть ситуации когда перекрестная энтропия — это именно то, что нас волнует, но это не всегда так. Гораздо чаще мы не знаем точно, что нас волнует, и перекрестная энтропия — действительно хороший прокси.

Информация дает нам сильную новую базу для размышления о мире. Иногда она идеально подходит для данной задачи; в других случаях не совсем, но все же чрезвычайно полезна. Это эссе только поскребло поверхность теории информации – есть основные темы, такие как коды исправления ошибок, которые мы вообще не касались, но я надеюсь, что я показал, что теория информации — это прекрасный предмет, который не должен быть пугающим.

Источник

Неравномерное кодирование. Средняя длина кодирования

Кодирование Хаффмана (часть 1 и 2)

SadKo
Владимир Садовников

Комментарии

Joint Source-Channel Coding and Decoding

Joint source-channel variable-length codes

Information Theory

9.3 Source Coding Theorem

Solution

Lossless compression methods

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

7.2.2 Entropy, efficiency, and redundancy

7.2.3 Prefix codes and unique decodability

Lossless Compression Methods

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

7.2.2 Entropy, efficiency, and redundancy

7.2.3 Prefix codes and unique decodability

Digital Image Compression

Information Measure

Performance improvement methods

6.2.2.2 Side-effect on inference accuracy

Неравномерное кодирование. Средняя длина кодирования

Префиксные коды

Вычисление энтропии

Перекрестная энтропия

Энтропия и несколько переменных

Взаимная информация

Дробные биты

Заключение

Не пропустите также:

Неравномерное кодирование. Средняя длина кодирования

Кодирование Хаффмана (часть 1 и 2)

SadKo Владимир Садовников

Комментарии

Joint Source-Channel Coding and Decoding

Joint source-channel variable-length codes

Information Theory

9.3 Source Coding Theorem

Solution

Lossless compression methods

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

7.2.2 Entropy, efficiency, and redundancy

7.2.3 Prefix codes and unique decodability

Lossless Compression Methods

7.2 Symbol encoding

7.2.1 A generic model for lossless compression

7.2.2 Entropy, efficiency, and redundancy

7.2.3 Prefix codes and unique decodability

Digital Image Compression

Information Measure

Performance improvement methods

6.2.2.2 Side-effect on inference accuracy

Неравномерное кодирование. Средняя длина кодирования

Префиксные коды

Вычисление энтропии

Перекрестная энтропия

Энтропия и несколько переменных

Взаимная информация

Дробные биты

Заключение

Не пропустите также:

SadKo
Владимир Садовников