Как найти средний угол окружности - AvtoShod.ru - решение различных проблем

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Вам будет интересно: Пурпурные бактерии — описание, особенности и интересные факты

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

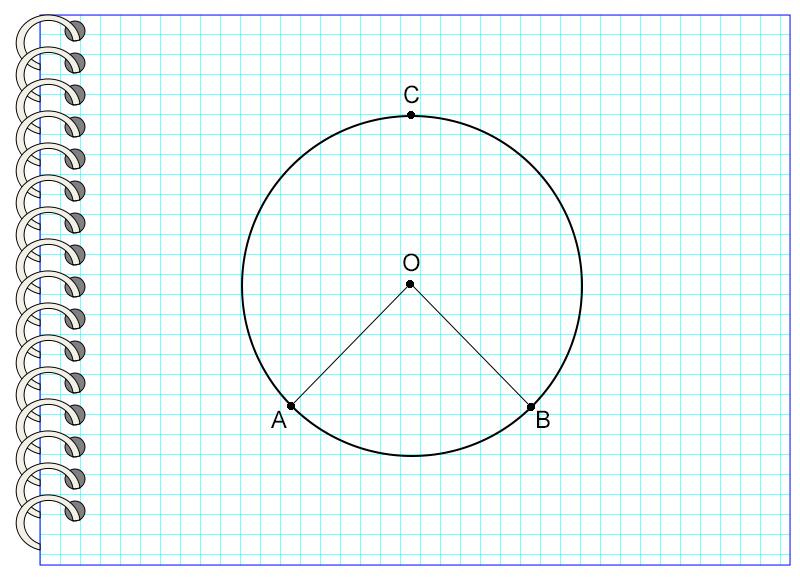
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

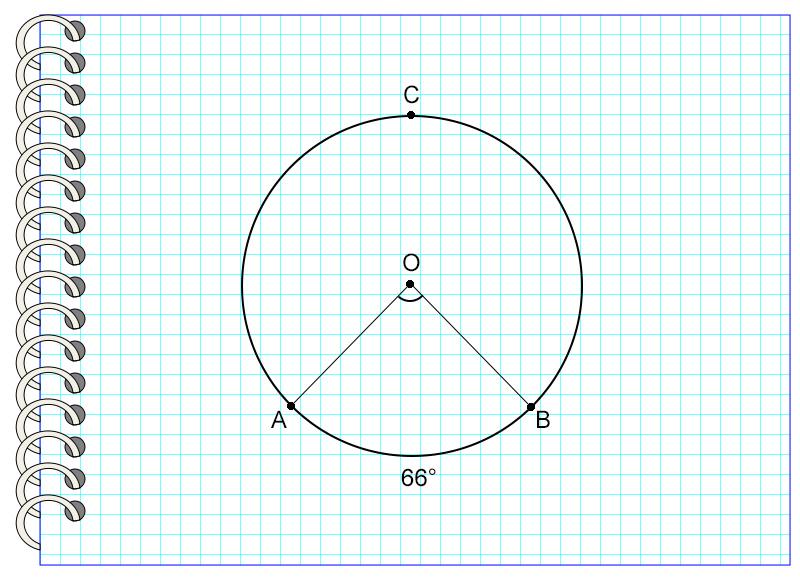
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Вам будет интересно: Площадь боковой поверхности и объем усеченной пирамиды: формулы и пример решения типовой задачи

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

Приведем следующий пример.

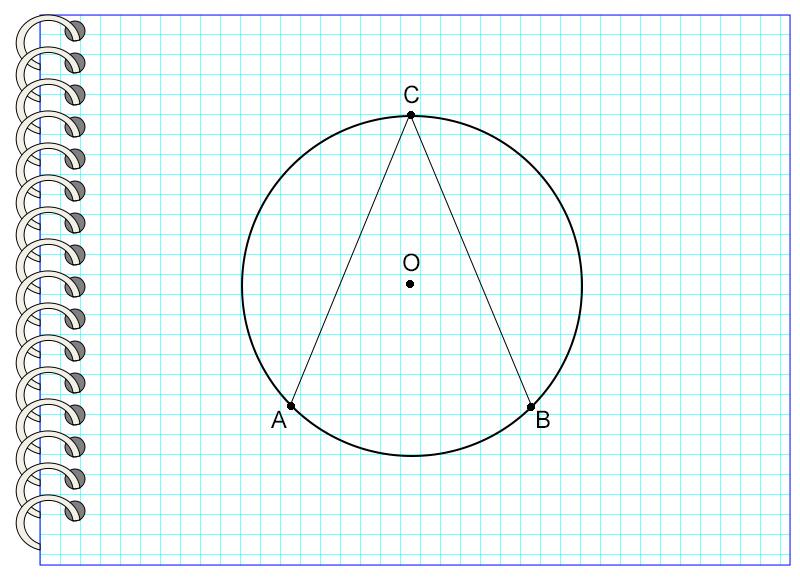
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

Вам будет интересно: Профиль крыла самолета: виды, технические и аэродинамические характеристики, метод расчета и наибольшая подъемная сила

Итак, центральный угол равен градусной мере дуги, на которую он опирается.

На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

Таким образом, центральные углы, опирающиеся на равные дуги, равны.

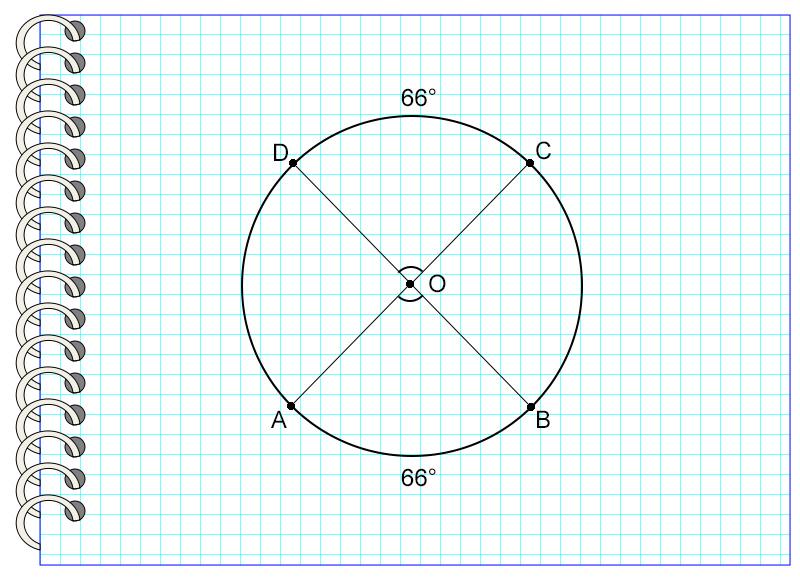
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

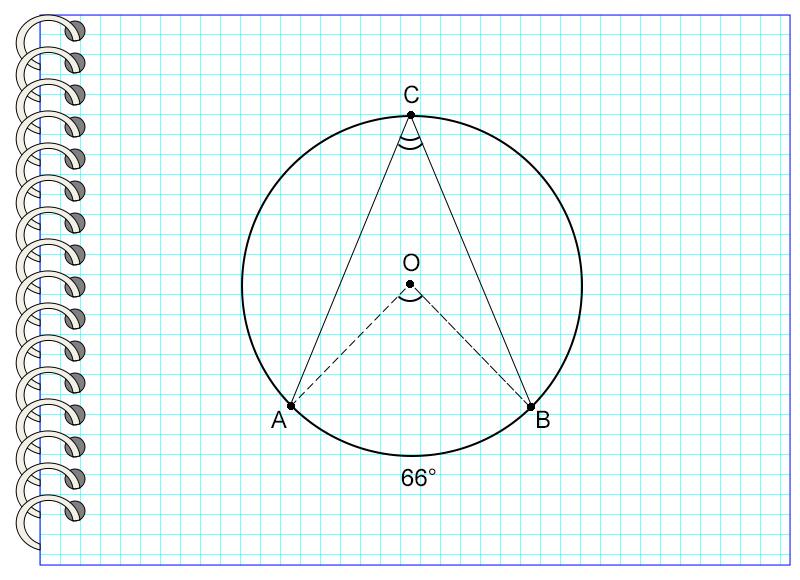
Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

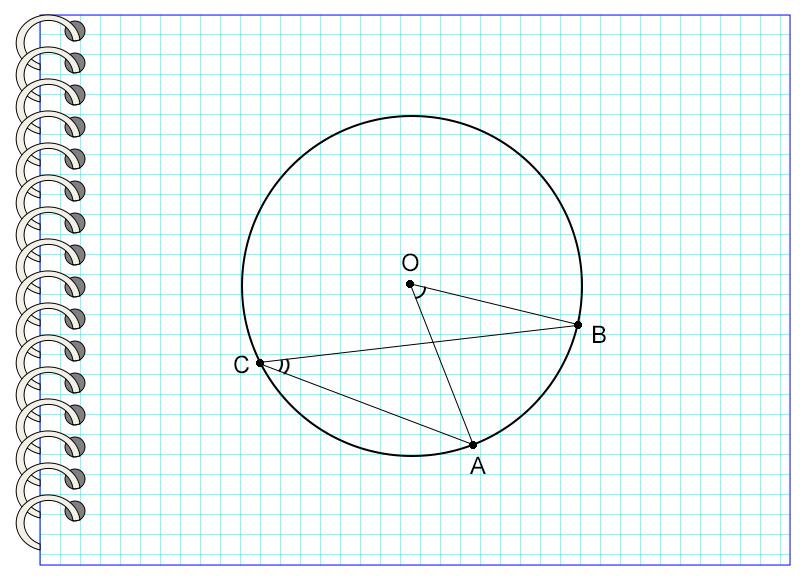
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° — АС — АВ

ВС = 360° — 120° — 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° — 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° — 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

источники:

http://www.resolventa.ru/spr/planimetry/cangle.htm

http://1ku.ru/obrazovanie/44602-ugly-v-okruzhnosti-centralnyj-i-vpisannyj-svojstva-i-sposoby-nahozhdenija/

Источник

msm.ru

Нравится ресурс?
Помоги проекту!

правила раздела Алгоритмы

1. Помните, что название темы должно хоть как-то отражать ее содержимое (не создавайте темы с заголовком ПОМОГИТЕ, HELP и т.д.). Злоупотребление заглавными буквами в заголовках тем ЗАПРЕЩЕНО.
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code…/code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии «срочно надо», заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке

Нахождение среднего угла

Подписаться на тему
Сообщить другу
Скачать/распечатать тему

Сообщ.
#1

,
12.07.07, 11:16

Помогите пожалуйста … уперся в проблему :wall: …

Задача:
Есть набор точек расположенных по отношению к центру координат под разными углами.
Интервал величин 0-360 градусов
Надо найти среднюю величину угла для данных точек

Например:
имеем 3 точки расположеные под углами 359, 1 и 6 градусов соответственно …
глядя на это очевидно что средний угол будет ((359-360) + 1 + 6)/3 = 2 градуса …

Но вот как понять что в случае с 359 величину надо отнимать от 360 чтобы получить -1
а в случае 1 и 6 не надо … ?
И если предположить что углы до какой-то величины считать отрицательными о после какой-то положительными до тогда до какой?

Причем надо знать что угол именно 359 а не 181 градус т.е. просто считать среднее по синусам например не получится …

Спасибо

П/С:
Задача в том чтобы в пространстве Хафа линии сгруппировать по минимальному расстоянию и заменить на одну со средними радиусом и углом

Swindler

Сообщ.
#2

,
12.07.07, 11:20

Цитата maksimz @ 12.07.07, 11:16

Но вот как понять что в случае с 359 величину надо отнимать от 360 чтобы получить -1

смотреть что точка попала в 3 или 4 четверть? тоесть если угол больше 180, то угол =угол -360

maksimz

Сообщ.
#3

,
12.07.07, 11:38

помоему получится та же проблема со сменой знака … т.е. 181, 179 и 174 градуса … среднее 178

а если по четвертям то 181 в 3-ей четверти и значит 181-360=-179 -> (-179+179+174)/3 = 174/3

Добавлено 12.07.07, 11:40
я еёе понимаю как минимальное расстояние посчитать между углами но пока это не помогает

Минимальное расстояние:
Пусть а1 и а2 углы то минимальное расстояние между ними мр=а1-а2 если мр>180 то мр=360-мр

MBo

Сообщ.
#4

,
12.07.07, 14:19

сложить единичные векторы, направленные под нужными углами(Cos(fi[i]), Sin(f[i])), и вычислить угол (направление) результирующего вектора.

AVA12

Сообщ.
#5

,
12.07.07, 14:52

Гм. Если я правильно понял задачу, то решение элементарно:

Строим векторы одинаковой длины, которые образуют с осью заданные углы. Складываем эти векторы. Сумма векторов как раз и задает «средний» азимут.

По-моему, так.

maksimz

Сообщ.
#6

,
12.07.07, 15:16

спасибо
предпоследнее решение вроде работает

Го_

Сообщ.
#7

,
13.07.07, 11:52

Junior

Цитата maksimz @ 12.07.07, 15:16

предпоследнее решение вроде работает

Так получится не средняя величина угла.

Pacific

Сообщ.
#8

,
13.07.07, 15:49

Senior Member

Рейтинг (т): 30

Го_
Ну да: arcsin((sin(30)+sin(45))/2) != (30+45)/2

Тогда нужно складывать именно значения углов, а оси проводить так, чтобы все углы попали в интервал (0, pi). Если оси провести так не удастся, значит, не судьба Хотя… Можно отдельно посчитать средний угол для интервала (0, pi) и средний угол для интервала (pi, 2*pi) и сложить их с соответствующими весовыми коэффициентами. Нужно требовать от автора строгое определение того, что нужно вычислить. Тогда он и сам разберется :yes:

Еще один прикол: какой будет средний угол для углов 0 и 180? Он может быть равен 90 (если мы их рассматриваем как 0 и 180), и -90 (если мы их рассматриваем как 0 и -180). Направления прямо противоположные

Сообщение отредактировано: Pacific — 13.07.07, 16:01

maksimz

Сообщ.
#9

,
18.07.07, 13:38

На самом деле про «предпоследнее решение которое вроде работает» это о том что оно решает мою проблему … а проблема смотри П/С первого сообщения

На сколько я его понял надо посчитать сумму синусов и сумму косинусов для углов среднее для которых надо найти и угол которому соответствуют полученые значения и есть искомый т.е. если имеем sum(sin(a)) и sum(cos(a)) то а это искомый угол и лично я решил что могу найти его как:
а=arctg(sum(sin(a))/sum(cos(a)))

Может я и ошибаюсь но подсчитав по нескольким вариантам получил то что и надо … отсюда и «вроде работает»

По поводу 0 и 180 … точки в пространстве Хафа (получаемого после преобразования Хафа на некотором изображении)
насколько я понимаю задаются полярными координатами т.е. если имеем 2 точки расположенные к центру под 0 и под 180 это означает что они соответствуют 2м параллельным прямым расположенным по разные стороны от центра и соответственно вопрос о том можно ли их объединить в одну сводится к сумме расстояний между ними и при условии что можно то средний угол я и не нахожу вообще

а переношу добавляемую точку в тот же квадрант в котором находится точка к которой я её добавляю

т.е. да я согласен что проблему не описал полностью … но полного описания как оказалось и не требовалось …

Сообщение отредактировано: maksimz — 18.07.07, 13:39

Velas

Сообщ.
#10

,
30.05.17, 20:53

maksimzСтолкнулся с вашей древней задачей о нахождении среднего значения между направлениями.
Решение:(Вы уж просите, я геодезист)
1. считаем, что направление это это угол (левый угол), отсчитываемый от точки северва по часовой стрелке и изменяющийся от 0 до 359.999(9);
2. исходя из 1 считаем, что существует предел в 360 градусов, но направление может быть только 0, однако из-за арифметических действий
возникает переполнение.;
3. Есть 2 или более направления — веер направлений, кол-во N. Приведём их к общему началу FirsnAl. В результате получим веер направлений в
котором любое направление Al[i] находится в пределах 0<=Al < Lim(360). Берём среднее Meam. Окончательный результат — Meam + First.

Var
BеерDirect : Array(1..N) of real;
tmp : Array(1..N) of real;
First : Real;
Summ : Real;
Meam : Real;
i : Integer;

//много лишнего, но для наглядности
//если считаете в радианах используйте масшабиррование и длинные целые.
Summ :=0;
First := BеерDirec;
for i := 1 to N do
begin
tmp[i] := BeepDirect[i] — First;
if tmp[i] <= 360 them
tmp[i] + 360;
Summ := Summ + tmp[i];
end;
Meam := Summ/N
Result := Meam + First;

1напр = 359 -359 = 0
2рапр = 001 -359 = 358 +360 = 2 / 2 = 1 + 359 = 0

MBo

Сообщ.
#11

,
31.05.17, 03:36

Velas
Что получится для примера автора 359, 1 и 6 градусов?
Или для углов 45, 315, 315?

amk

Сообщ.
#12

,
31.05.17, 16:02

Программа не работает.

После исправления ошибок будет работать, если углы лежат в пределах полукруга

Summ :=0;

First := BеерDirect[1];

for i := 1 to N do

begin

tmp := BeepDirect[i] — First;

if tmp[i] > 180 then

tmp = tmp — 360;

Summ := Summ + tmp;

end;

Result := Summ/N + First;

Если направления лежат большим веером то, во-первых, затруднительно вообще определить, что есть среднее направление.
Первый вариант, дающий такое же решение для узких секторов, выбрать направление, минимизирующее сумму квадратов отклонений от него заданных углов. Но для некоторых наборов таких минимумов может быть несколько.
Другой. для каждого направления взять единичный направляющий вектор и в качестве среднего взять направление их суммы (если она отличается от нуля). Для малых разбросов результат почти совпадает.

Velas

Сообщ.
#13

,
31.05.17, 20:29

Ну да ‘апечатка’. First — это минимальное направление из веера(в общем случае любое). Отсортируем список
(или массив так проще для восприятия информации человеком, но не обязательно) измерений Имеем:359°—-(1)
359°—-)1)
1°——(4)
4°—-(359)
вычитаем из всех по 359—(1)
0°——(0)
2°——(3)
5°——(358)
ищем среднее
(0°+2°+ 5°)/3 = 2°20’00»—{(0+3+358)/3 = 361/3 = (361-360)/3 = 0°20’00»}
складываем с 359°—(1)
1°20’00»————(1°20’00»)

по другому прибавим ко всем направлениям по 1° (дополнение до 0°)
0°
2°
5°
ищем среднее
(0°+2°+ 5°)/3 = 2°20’00»
складываем с 359°
1°20’00»

направления это не углы т.к.
1 угол = 2°
2 угол = 3°
среднее
(2°+ 3°)/2 := 2°30’00»

Для
Что получится для примера автора 359, 1 и 6 градусов?
Или для углов 45, 315, 315?

Добавлено 31.05.17, 20:40
Разорвал текст, извините бывает.
Для MBo
Что получится для примера автора 359, 1 и 6 градусов?
Или для углов 45, 315, 315?

Углы Среднее = (45+315+315)/3 =255
направления = {((45-45)+(315-45)+(315-45))/3+45 = (0+270+270)/3+45 = 180/3+45 = 105°

Velas

Сообщ.
#14

,
31.05.17, 21:27

Схемка показывает, как измеряются направления

Прикреплённый файл____________________________________________________l.pdf (51,62 Кбайт, скачиваний: 308)

MBo

Сообщ.
#15

,
01.06.17, 04:04

Цитата

Для MBo
Или для углов 45, 315, 315?

Углы Среднее = (45+315+315)/3 =255
направления = {((45-45)+(315-45)+(315-45))/3+45 = (0+270+270)/3+45 = 180/3+45 = 105°

В обоих случаях арифметика подвела, получится и там, и там 225, но это не так важно.

Если ветер день дул на северо-восток, а два дня на северо-запад, то у тебя в среднем получится направление на юго-запад :wacko: :-?

Автор же описал, какие результаты для него (и в большинстве практических применений) адекватны, а в данном случае выходит вовсе не то.

0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)

0 пользователей:

Предыдущая тема
Алгоритмы
Следующая тема

[ Script execution time: 0,0836 ] [ 17 queries used ] [ Generated: 25.05.23, 03:02 GMT ]

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Средний угол

Добавлено: 15 мар 2017, 12:11

Начинающий

Зарегистрирован:
15 мар 2017, 12:01
Сообщений: 8
Cпасибо сказано: 0
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Задача состоит в том, что нужно найти средний угол угол на определённом расстоянии
[math]anglevarphi[/math] увеличивается от [math]0^{circ}[/math] на [math]L_0[/math] до [math]180^{circ}[/math] на [math]L_1[/math]
То есть
[math]anglevarphi(L_0) = 0^{circ}[/math]
[math]anglevarphi(L_1) = 180^{circ}[/math]

Вернуться к началу

Znatniy	Заголовок сообщения: Re: Средний угол Добавлено: 15 мар 2017, 12:52
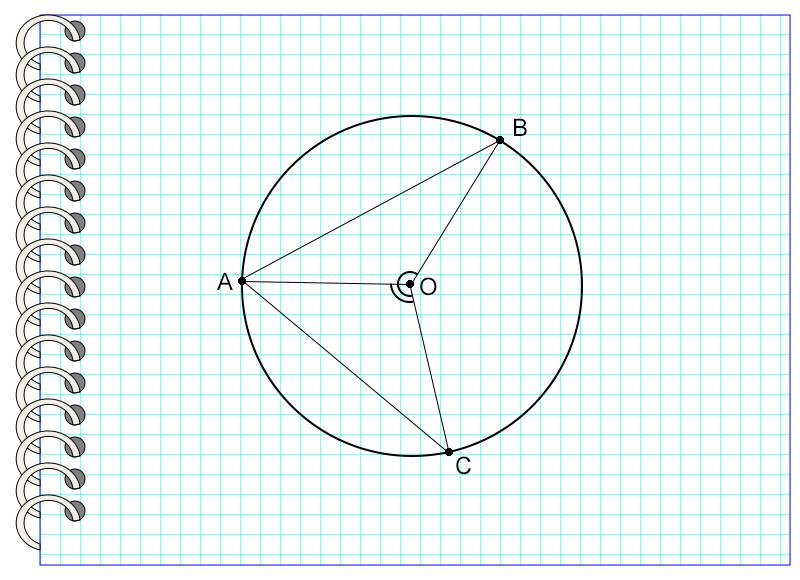
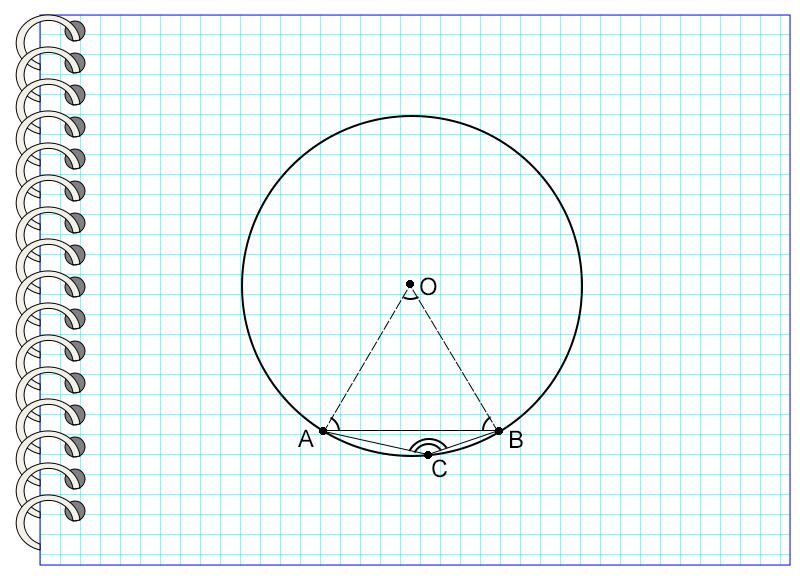
	Иллюстрации к задаче
Вернуться к началу

Znatniy	Заголовок сообщения: Re: Средний угол Добавлено: 15 мар 2017, 16:20
	Да, вы всё правильно поняли. Я не знаю, как решить эту задачу точно и математически верно
Вернуться к началу

Znatniy	Заголовок сообщения: Re: Средний угол Добавлено: 15 мар 2017, 16:40
	Не совсем так. Под средним углом я подразумеваю угол, который будет на всём этом интервале Я решал эту задачу графически, рисовал окружности, определял углы и расстояния. По полученным значениям построил график в экселе, получил функцию в виде полинома, проинтегрировал её и получил [math]approx138^{circ}[/math] И нет, угол [math]2 pi slash 3[/math] на расстоянии 0,89 R
Вернуться к началу

Andy	Заголовок сообщения: Re: Средний угол Добавлено: 15 мар 2017, 16:45
	Znatniy Такое объяснение Znatniy писал(а): Под средним углом я подразумеваю угол, который будет на всём этом интервале непонятно. Поэтому попробуйте объяснить иначе. Думаю, что интегрирование здесь не нужно.
Вернуться к началу

Andy	Заголовок сообщения: Re: Средний угол Добавлено: 15 мар 2017, 16:51
	Znatniy Znatniy писал(а): И нет, угол [math]2 pi slash 3[/math] на расстоянии 0,89 R Как Вы это установили? Предложенной мной формуле Вы не доверяете? Что ж, проверьте графически. Вспомните и примените теорему о катете прямоугольного треугольника, лежащем против угла в [math]30^{circ}.[/math]
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Средний объем в форуме Математическая статистика и Эконометрика	atobor	3	341	27 сен 2014, 00:31
Средний процент. 2 вопроса в форуме Математическая статистика и Эконометрика	Kotoff	2	221	13 авг 2020, 10:28
Средний радиус Земли в форуме Размышления по поводу и без	Avgust	37	901	18 мар 2020, 22:38
Средний возраст java ООП в форуме Информатика и Компьютерные науки	Katrina7	7	662	26 дек 2017, 19:25
Средний за 4 года уровень инфляции в форуме Экономика и Финансы	eprY	6	2111	05 янв 2014, 13:33
Средний процент продажи акций в форуме Математическая статистика и Эконометрика	shinshilla	0	530	10 ноя 2015, 12:33
Определить средний размер капитальных затрат в форуме Математическая статистика и Эконометрика	ens0nik	3	468	22 сен 2015, 18:43
Определить средний за 4 года уровень инфляции в форуме Экономика и Финансы	DanOO7	10	1975	16 апр 2014, 14:22
Шловикова Вадима Земли радиус средний в форуме Палата №6	Vadim Shlovikov	0	210	08 апр 2020, 17:57
Найти оценки зная их количество и средний бал в форуме Информатика и Компьютерные науки	RanokVechir	3	149	10 сен 2020, 13:48

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Усреднение углов… Опять

Я хочу вычислить среднее значение из набора углов, который представляет исходный азимут (от 0 до 360 градусов) — (аналогично направлению ветра)

Я знаю, что это обсуждалось ранее (несколько раз). Принятым ответом было вычислить единичные векторы по углам и взять угол их среднего.

Однако этот ответ определяет среднее не интуитивным способом. Среднее значение 0, 0 и 90 будет atan( (sin(0)+sin(0)+sin(90)) / (cos(0)+cos(0)+cos(90))) = atan(1/2)= 26,56 град

Я ожидаю, что среднее значение 0, 0 и 90 будет 30 градусов.

Поэтому я думаю, что было бы справедливо задать вопрос еще раз: как бы вы рассчитали среднее значение, поэтому такие примеры дадут интуитивный ожидаемый ответ.

Изменить 2014:

Задав этот вопрос, я разместил статью о CodeProject, в которой предлагается тщательный анализ. В статье рассматриваются следующие справочные задачи:

Приведенное время суток [00:00-24:00) для каждого рождения, произошедшего в США в 2000 году. Рассчитать среднее время рождения при рождении.
При наличии множества измерений направления от стационарного передатчика к стационарному приемнику с использованием методики измерения с обернутой нормальной распределенной ошибкой — оцените направление.
Учитывая мультимножество оценок азимута между двумя точками, сделанных «обычными» людьми (при условии, что они подверглись усеченной усеченной нормальной распределенной ошибке) — Оцените направление.

2009-11-28 19:19

11
ответов

Решение

Спасибо всем за то, что помогли мне увидеть мою проблему более четко.

Я нашел то, что искал. Это называется метод Мицуты.

Входы и выходы находятся в диапазоне [0..360).

Этот метод хорош для усреднения данных, которые были отобраны с использованием постоянных интервалов выборки.

В этом методе предполагается, что разница между последовательными выборками составляет менее 180 градусов (что означает, что если мы не будем производить выборку достаточно быстро, изменение дискретизированного сигнала на 330 градусов будет неправильно определено как изменение на 30 градусов в другом направлении и будет вставить ошибку в расчет). Теорема отсчетов Найквиста – Шеннона?

Вот код C++:

double AngAvrg(const vector<double>& Ang)
{
    vector<double>::const_iterator iter= Ang.begin();

    double fD   = *iter;
    double fSigD= *iter;

    while (++iter != Ang.end())
    {
        double fDelta= *iter - fD;

             if (fDelta < -180.) fD+= fDelta + 360.;
        else if (fDelta >  180.) fD+= fDelta - 360.;
        else                     fD+= fDelta       ;

        fSigD+= fD;
    }

    double fAvrg= fSigD / Ang.size();

    if (fAvrg >= 360.) return fAvrg -360.;
    if (fAvrg <  0.  ) return fAvrg +360.;
                       return fAvrg      ;
}

Это объясняется на странице 51 по адресу http://www.epa.gov/scram001/guidance/met/mmgrma.pdf

Спасибо Маре за отправку ссылки в качестве комментария.

Если данные выборки являются постоянными, но наше устройство для выборки имеет неточность с распределением фон Мизеса, будет уместным вычисление единичных векторов.

2009-12-01 19:11

[Обратите внимание, что вопрос ОП (но не заголовок), по-видимому, изменился на довольно специализированный вопрос («… среднее ПОСЛЕДОВАТЕЛЬНОСТИ углов, где каждое последующее сложение не отличается от скользящего среднего более чем на определенную величину».) — см. @MaR комментарий и мой.Мой следующий ответ касается названия ОП и основной части обсуждения и ответов, связанных с ним.]

Это не вопрос логики или интуиции, а определения. Это обсуждалось на SO раньше без какого-либо реального консенсуса. Углы должны быть определены в пределах диапазона (который может быть от -PI до +PI, или от 0 до 2*PI или может быть от -Inf до +Inf. Ответы будут разными в каждом случае.

Мир «угол» вызывает путаницу, поскольку это означает разные вещи. Угол зрения представляет собой величину без знака (и обычно это PI > theta > 0. В этом случае могут быть полезны «нормальные» средние значения. Угол поворота(например, общее вращение, если фигуристка) может или не может быть подписан и может включать в себя тета> 2* пи и тета <-2 * пи.

Здесь определяетсяугол = направление, для которого требуются векторы. Если вы используете слово «направление» вместо «угол», вы поймете намерение ОП (кажущийся оригинальным), и это поможет отойти от скалярных величин.

Википедия показывает правильный подход, когда углы определяются кругово, так что

theta = theta+2*PI*N = theta-2*PI*N

Ответом для среднего является НЕ скаляр, а вектор. ОП может не чувствовать, что это интуитивно понятно, но это единственный полезный правильный подход. Мы не можем переопределить квадратный корень из -4, чтобы он был равен -2, потому что это более наглядно — это должно быть +-2*i. Точно так же среднее значение подшипников -90 градусов и +90 градусов — это вектор нулевой длины, а не 0,0 градусов.

Википедия ( http://en.wikipedia.org/wiki/Mean_of_circular_quantities) имеет специальный раздел и состояния (Уравнения LaTeX и их можно увидеть в Википедии):

Большинство обычных средних значений терпят неудачу на круглых величинах, таких как углы, дневное время, дробные части действительных чисел. Для этих величин вам нужно среднее значение круговых величин.

Поскольку среднее арифметическое не является эффективным для углов, можно использовать следующий метод для получения как среднего значения, так и показателя дисперсии углов:

Переведите все углы в соответствующие точки на единичной окружности, например, α в (cosα,sinα). То есть конвертировать полярные координаты в декартовы. Затем вычислите среднее арифметическое этих точек. Полученная точка будет лежать на диске устройства. Переведите эту точку обратно в полярные координаты. Угол является разумным средним из входных углов. Результирующий радиус будет 1, если все углы равны. Если углы равномерно распределены по окружности, то результирующий радиус будет равен 0, а круговое среднее отсутствует. Другими словами, радиус измеряет концентрацию углов.

Учитывая углы alpha_1,dots,alpha_n, среднее значение вычисляется как
M alpha = operatorname{atan2}left(frac{1}{n}cdotsum_{j=1}^n
sinalpha_j,
frac{1}{n}cdotsum_{j=1}^n
cosalpha_jright)

используя вариант функции арктангенса atan2, или
M alpha = argleft(frac{1}{n}cdotsum_{j=1}^n
Ехр ( CDOT alpha_j) справа)

используя комплексные числа.

Обратите внимание, что в вопросе OP угол 0 является чисто произвольным — нет ничего особенного в том, что ветер приходит от 0, а не к 180 (за исключением того, что в этом полушарии на велосипеде холоднее). Попробуйте изменить 0,0,90 на 289, 289, 379 и посмотрите, как простая арифметика больше не работает.

(Есть некоторые распределения, где углы 0 и PI имеют особое значение, но они здесь не входят в объем).

Вот некоторые интенсивные предыдущие обсуждения, которые отражают текущее распространение взглядов:-)

http://mathforum.org/library/drmath/view/53924.html

Как вы рассчитываете среднее значение для набора циклических данных?

http://forums.xkcd.com/viewtopic.php?f=17&t=22435

http://www.allegro.cc/forums/thread/595008

2009-11-28 21:15

Что это вообще значит для среднего источника подшипников? Начните с ответа на этот вопрос, и вы приблизитесь к тому, чтобы определить, что вы подразумеваете под средним углом.

На мой взгляд, угол с касательной, равной 1/2, является правильным ответом. Если у меня есть единичная сила, толкающая меня в направлении вектора (1, 0), другая сила, толкающая меня в направлении вектора (1, 0), и третья сила, толкающая меня в направлении вектора (0, 1).), то результирующая сила (сумма этих сил) — это сила, толкающая меня в направлении (1, 2). Это векторы, представляющие подшипники 0 градусов, 0 градусов и 90 градусов. Угол, представленный вектором (1, 2), имеет касательную, равную 1/2.

Отвечая на ваше второе редактирование:

Допустим, мы измеряем направление ветра. Наши 3 измерения были 0, 0 и 90 градусов. Поскольку все измерения одинаково надежны, почему наша лучшая оценка направления ветра не должна составлять 30 градусов? установка его на 25,56 градусов — это смещение в сторону 0…

Хорошо, вот проблема. Единичный вектор с углом 0 не обладает такими же математическими свойствами, как действительное число 0. Использование обозначений 0v чтобы представить вектор с углом 0, обратите внимание, что

0v + 0v = 0v

ложно, но

0 + 0 = 0

верно для реальных чисел. Так что если 0v представляет ветер с единичной скоростью и углом 0, то 0v + 0v ветер с удвоенной единицей скорости и углом 0. А потом, если у нас есть третий вектор ветра (который я буду представлять с помощью обозначения 90v), который имеет угол 90 и единичную скорость, то ветер, возникающий из суммы этих векторов, имеет уклон, потому что он движется с удвоенной частотой вращения в горизонтальном направлении, но только с единичной скоростью в вертикальном направлении.

user45914

29 ноя ’09 в 18:08
2009-11-29 18:08

2009-11-29 18:08

Это неверно на каждом уровне.

Векторы добавляются в соответствии с правилами сложения векторов. «Интуитивный, ожидаемый» ответ может быть не таким интуитивным.

Возьмите следующий пример. Если у меня есть один единичный вектор (1, 0) с источником в (0,0), который указывает в направлении +x, и другой (-1, 0), который также имеет начало в (0,0), который указывает в -x-направление, каким должен быть «средний» угол?

Если я просто добавлю углы и разделю на два, я могу утверждать, что «среднее» составляет либо +90, либо -90. Как вы думаете, какой из них должен быть?

Если я добавлю векторы в соответствии с правилами сложения векторов (компонент за компонентом), я получу следующее:

(1, 0) + (-1, 0) = (0, 0)

В полярных координатах это вектор с нулевой величиной и нулевым углом.

Так каким должен быть «средний» угол? У меня есть три разных ответа для простого случая.

Я думаю, что ответ заключается в том, что векторы не подчиняются той же интуиции, что и числа, потому что они имеют величину и направление. Может быть, вам лучше описать, какую проблему вы решаете.

Какое бы решение вы ни выбрали, я бы посоветовал вам основывать его на векторах. Так будет всегда правильно.

user37213

28 ноя ’09 в 19:33
2009-11-28 19:33

2009-11-28 19:33

Изменить: Эквивалентный, но более надежный алгоритм (и более простой):

разделить углы на 2 группы, [0-180) и [180-360)
численно среднее значение обеих групп
усредните 2 средних по группе с правильным взвешиванием
если произошло завертывание, исправить на 180˚

Это работает, потому что усреднение чисел работает «логически», если все углы находятся в одном и том же полукруге. Затем мы откладываем получение ошибки обтекания до самого последнего шага, где ее легко обнаружить и исправить. Я также добавил некоторый код для обработки случаев с противоположными углами. Если средние значения противоположны, мы отдаем предпочтение полусфере, в которой было больше углов, а в случае равных углов в обоих полушариях мы возвращаемся None потому что никакой средний не будет иметь смысла.

Новый код:

def averageAngles2(angles):
    newAngles = [a % 360 for a in angles];
    smallAngles = []
    largeAngles = []
    # split the angles into 2 groups: [0-180) and [180-360)
    for angle in newAngles:
        if angle < 180:
            smallAngles.append(angle)
        else:
            largeAngles.append(angle)
    smallCount = len(smallAngles)
    largeCount = len(largeAngles)
    #averaging each of the groups will work with standard averages
    smallAverage = sum(smallAngles) / float(smallCount) if smallCount else 0
    largeAverage = sum(largeAngles) / float(largeCount) if largeCount else 0
    if smallCount == 0:
        return largeAverage
    if largeCount == 0:
        return smallAverage
    average = (smallAverage * smallCount + largeAverage * largeCount) / 
        float(smallCount + largeCount)
    if largeAverage < smallAverage + 180:
        # average will not hit wraparound
        return average
    elif largeAverage > smallAverage + 180:
        # average will hit wraparound, so will be off by 180 degrees
        return (average + 180) % 360
    else:
        # opposite angles: return whichever has more weight
        if smallCount > largeCount:
            return smallAverage
        elif smallCount < largeCount:
            return largeAverage
        else:
            return None

>>> averageAngles2([0, 0, 90])
30.0
>>> averageAngles2([30, 350])
10.0
>>> averageAngles2([0, 200])
280.0

Вот немного наивный алгоритм:

убрать все углы откоса из списка
взять пару углов
поверните их в первый и второй квадрант и усредните их
повернуть средний угол назад на ту же величину
для каждого оставшегося угла усредните таким же образом, но с последовательно увеличивающимся весом до составного угла

некоторый код на Python (шаг 1 не реализован)

def averageAngles(angles):
    newAngles = [a % 360 for a in angles];
    average = 0
    weight = 0
    for ang in newAngles:
        theta = 0
        if 0 < ang - average <= 180:
            theta = 180 - ang
        else:
            theta = 180 - average
        r_ang = (ang + theta) % 360
        r_avg = (average + theta) % 360
        average = ((r_avg * weight + r_ang) / float(weight + 1) - theta) % 360
        weight += 1
    return average

user73681

28 ноя ’09 в 19:35
2009-11-28 19:35

2009-11-28 19:35

Вот ответ, который я дал на этот же вопрос:

Как вы рассчитываете среднее значение для набора циклических данных?

Это дает ответы в соответствии с тем, что ОП говорит, что он хочет, но внимание должно быть уделено этому:

«Я также хотел бы подчеркнуть, что хотя это истинное среднее углов, в отличие от векторных решений, это не обязательно означает, что это решение, которое вы должны использовать, среднее значение соответствующих единичных векторов вполне может быть значением, которое вы на самом деле следует использовать «.

2010-09-06 13:52

На мой взгляд, речь идет об углах, а не векторах. По этой причине среднее значение 360 и 0 действительно равно 180. Среднее значение за один оборот и без поворотов должно быть половиной оборота.

2009-11-28 19:38

Возможно, вы могли бы представить углы как кватернионы и взять среднее значение этих кватернионов и преобразовать их обратно в угол.

Я не знаю, дает ли это вам то, что вы хотите, потому что кватернионы — это скорее вращения, чем углы. Я также не знаю, даст ли это вам что-то отличное от векторного решения.

Кватернионы в 2D упрощаются до комплексных чисел, так что я думаю, что это просто векторы, но, возможно, какой-нибудь интересный алгоритм усреднения кватернионов, например http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20070017872_2007014421.pdf при упрощении до 2D будет вести себя лучше, чем просто векторное среднее.

2009-12-01 21:19

Вы можете сделать это: скажем, у вас есть набор углов в массиве angleЗатем для вычисления массива сначала выполните: angle[i] = angle[i] mod 360Теперь выполните простое среднее по массиву. Поэтому, когда у вас есть 360, 10, 20, вы в среднем 0, 10 и 20 — результаты интуитивно понятны.

2009-11-28 19:34

Ну вот! Ссылка https://www.wxforum.net/index.php?topic=8660.0

def avgWind(directions):
    sinSum = 0
    cosSum = 0
    d2r = math.pi/180 #degree to radian
    r2d = 180/math.pi
       
    for i in range(len(directions)):
        sinSum += math.sin(directions[i]*d2r)
        cosSum += math.cos(directions[i]*d2r)
      
    return ((r2d*(math.atan2(sinSum, cosSum)) + 360) % 360)
a= np.random.randint(low=0, high=360, size=6)
print(a)
avgWind(a)

2020-11-06 07:08

Что плохого в том, чтобы принимать набор углов в качестве реальных значений и просто вычислять среднее арифметическое этих чисел? Тогда вы получите интуитивный (0+0+90)/3 = 30 градусов.

Редактировать: Спасибо за полезные комментарии и указание, что углы могут превышать 360. Я считаю, что ответом может быть обычное среднее арифметическое значение, уменьшенное по модулю 360: мы суммируем все значения, делим на количество углов и затем вычитаем / добавляем кратное 360, так что результат лежит в интервале [0..360).

2009-11-28 19:24

Я думаю, что проблема связана с тем, как вы относитесь к углам больше 180 (и к углам больше 360). Если вы уменьшите углы до диапазона от +180 до -180, прежде чем добавить их к общему значению, вы получите нечто более разумное:

int AverageOfAngles(int angles[], int count)
{
    int total = 0;
    for (int index = 0; index < count; index++)
    {
        int angle = angles[index] % 360;
        if (angle > 180) { angle -= 360; }
        total += angle;
    }

    return (int)((float)total/count);
}

user33686

28 ноя ’09 в 19:41
2009-11-28 19:41

2009-11-28 19:41

Источник

План урока:

Центральный угол и градусная мера дуги

Вписанный угол

Углы между хордами и секущими

Теорема о произведении отрезков хорд

Задачи на квадратной решетке

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Решение.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Ответ: 120°.

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠OCA = ∠OAC = α

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

⋃BC = 2α

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN — ⋃MN = 180° — 70° = 110°

Ответ: 110°.

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Ответ: 63°.

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Решение.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Решение.

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Решение.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

α/2 + β/2 = (α + β)/2

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

Ответ: 40°.

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Ответ: 44°.

Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

AK*KD = CK*BK

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Решение.

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

AM*MB = CM*MD

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Ответ: 3,8.

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

∠ABC = 90°:2 = 45°

Ответ: 45°.

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Ответ: 135°.

Задание. Чему равен ∠AВС на рисунке?

Решение.

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

Источник

Доказательства теорем об углах, связанных с окружностью

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Что такое центральный угол?

Чем вписанный угол отличается от центрального?

Чему равен центральный угол

Как найти вписанный угол

Где могут встретиться задачи на эту тему? Их виды и способы решения

Углы, опирающиеся на одну дугу

Углы, опирающиеся на разные дуги одной окружности

Задачи, основанные на соотношении дуг

Кто сейчас на конференции

Усреднение углов… Опять

11 ответов

Центральный угол и градусная мера дуги

Вписанный угол

Углы между хордами и секущими

Теорема о произведении отрезков хорд

Задачи на квадратной решетке

Не пропустите также:

11
ответов