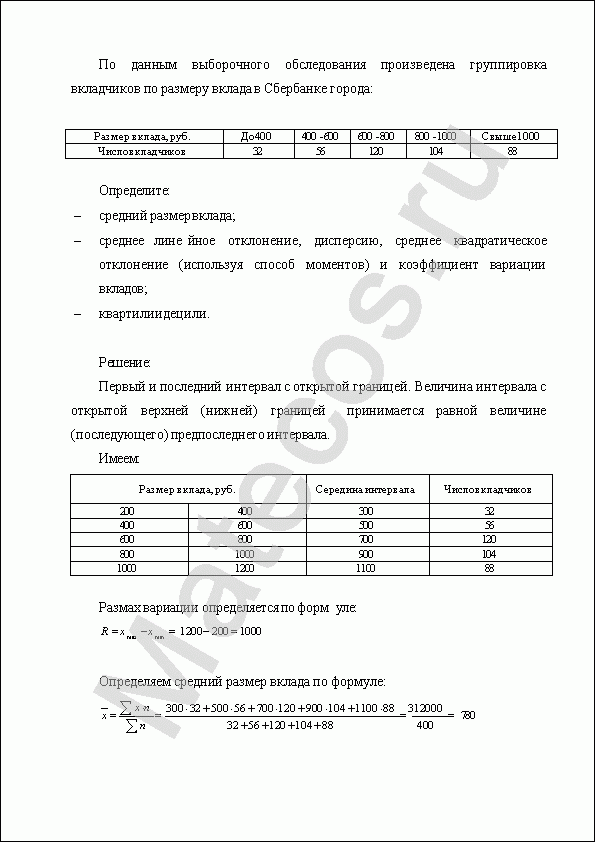
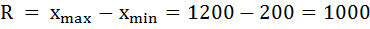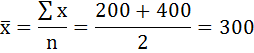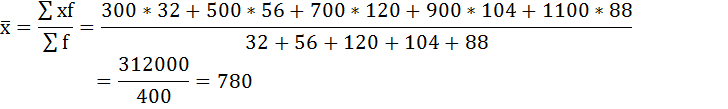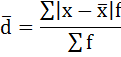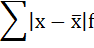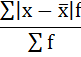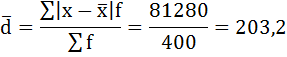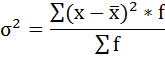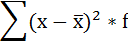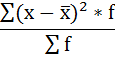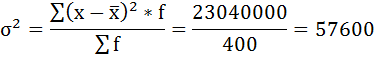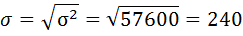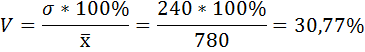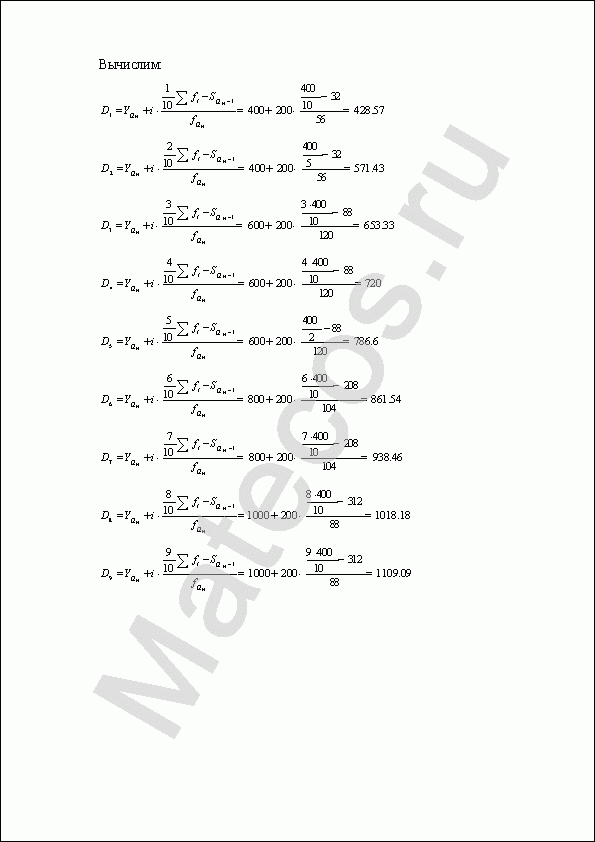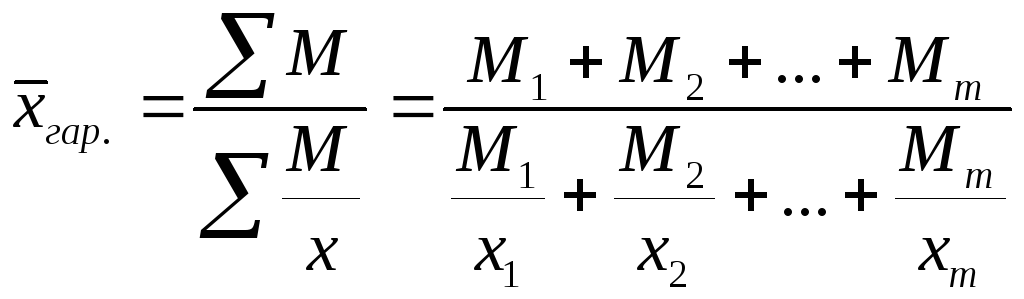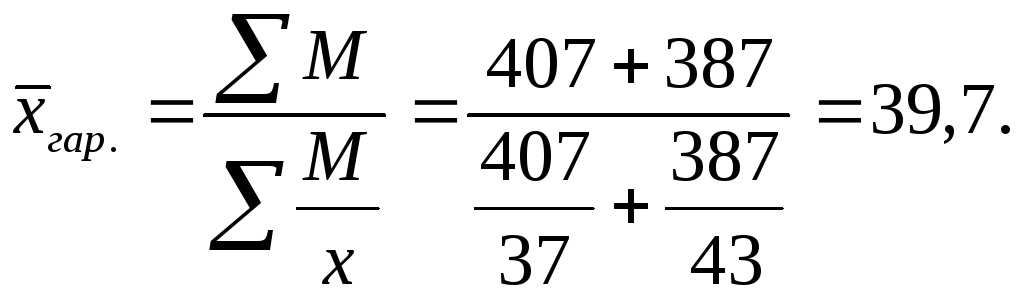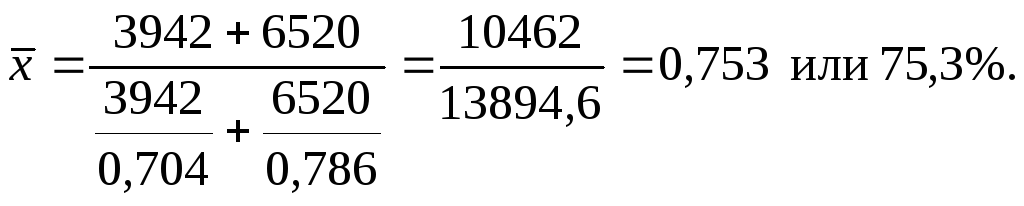По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Номер задачи: S-56
Решение: бесплатно
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400-600 | 600-800 | 800-1000 | Свыше 1000 |
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
-
средний размер вклада;
-
среднее линейное отклонение, дисперсию, среднее квадратическое отклонение (используя способ моментов) и коэффициент вариации вкладов;
-
квартили и децили.
Похожие работы:
Задачи по статистике с решением — Средние величины
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:


|
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
|
1 2 3 4 5 |
18 18 19 20 19 |
6 7 8 9 10 |
20 19 19 19 20 |
11 12 13 14 15 |
22 19 19 20 20 |
16 17 18 19 20 |
21 19 19 19 19 |
Если сгруппировать данные, то получим ряд распределения:


2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт., Хi |
18 |
19 |
20 |
21 |
22 |
Всего |
|
Число рабочих, fi |
2 |
11 |
5 |
1 |
1 |
20 |


3. Задача на вычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет. |
Число рабочих, чел., fi |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
ИТОГО: |
200 |


4. Задача на вычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
|
Группы рабочих по оплате труда у.е. |
Число рабочих, чел. |
Середина интервала, хi |
|
До 500 |
5 |
450 |
|
500-600 |
15 |
550 |
|
600-700 |
20 |
650 |
|
700-800 |
30 |
750 |
|
800-900 |
16 |
850 |
|
900 и более |
14 |
950 |
|
Итого: |
100 |
— |

Задача 5. Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий |
Середина интервалов, х |
|
Хi*f |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
Итого: |
25 |
— |
— |
0 |
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i— величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I, получим новый вариационный ряд распределения новых вариантов хi. Средняя арифметическая их новых вариантов- момент первого порядка m i= 

Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
|
Предприятие |
Численность промышленно- производственного персонала, чел |
Месячный фонд заработной платы, тыс руб. |
Средняя заработная плата, руб. |
|
А |
1 |
2 |
3 |
|
1 2 3 |
540 275 458 |
564,84 332,75 517,54 |
1046 1210 1130 |
|
ИТОГО: |
1 273 |
1415,13 |
? |
Определить среднюю з/п по всем предприятиям.
Решение:
Составим логическую формулу средней: средняя з/п по всем предприятиям =
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной:

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.


3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
|
№ магазина |
Цена моркови., руб за кг. |
Выручка от реализации, руб. |
|
1 2 3 |
17 20 24 |
3060 2800 1920 |
|
Итого: |
— |
7780 |
Решение.
Логическая формула средней: средняя цена моркови =
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
|
Вид вклада |
Октябрь |
Ноябрь |
||
|
Число вкладов, тыс., f |
Средний размер вклада, руб., x |
Сумма вкладов, млн. руб., F |
Средний размер вклада, x |
|
|
До востребования Срочный |
10 8 |
350 400 |
4,07 3,87 |
370 430 |
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:


2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:


2) решение по средней арифметической взвешенной



Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3)
Информация о вкладах в банке для расчета средних значений
|
Октябрь |
Ноябрь |
|||
|
Вид |
Число f |
Средний тыс. х |
Сумма млн. М |
Средний размер вклада, тыс. х |
|
До |
10 |
35 |
4,07 |
37 |
|
Срочный |
8 |
40 |
3,87 |
43 |
В
октябре известен средний размер вкладов
каждого вида х
и количество вкладов f.
Следовательно, для расчета среднего
размера вклада по двум видам применяем
формулу средней арифметической
взвешенной, тыс. руб.:
В ноябре известен средний размер вкладов
каждого вида, а количество вкладов не
известно, но зато имеются данные об
общих суммах вкладов.
Путем
деления сумм вкладов М каждого вида на
их средний размер вклада х
можно определить веса – число вкладов
по их видам f,
а затем определить средний размер вклада
по двум видам по формуле средней
арифметической.
Однако,
если в расчете использовать среднюю
гармоническую, то отпадает необходимость
предварительного расчета весов –
размеров вкладов по каждому виду,
поскольку эта операция заложена в саму
формулу. Средняя гармоническая взвешенная
применяется, когда статистическая
информация не содержит частот f
по отдельным единицам совокупности, а
представлена как произведение xf.
Чтобы исчислить среднюю, обозначим
xf=М,
откуда f=w/x. Преобразуем формулу средней
арифметической так, чтобы по имеющимся
данным x
и М можно было исчислить среднюю.
В
формулу средней арифметической взвешенной
вместо xf
подставим
М, вместо f
– отношение М/x
и получим формулу средней гармонической
взвешенной:
Итак, средний
размер вклада в ноябре по двум их видам
находим по формуле средней гармонической
взвешенной, тыс. руб.:
Пример
5. В результате
проверки двух партий муки потребителям
установлено, что в первой партии муки
высшего сорта было 3942 кг., что составляет
70,4% общего веса муки этой партии. Во
второй партии муки высшего сорта было
6520 кг., что составляет 78,6% общего веса
муки этой партии. Определите процент
муки высшего сорта в среднем по первой
и второй партиям вместе.
Решение
Средний процент
муки высшего сорта по двум партиям
определяем по формуле средней гармонической
взвешенной:
Средняя геометрическая
Пример
1.
Предположим, Вы внесли деньги в банк на
срочный депозит, процент по которому
ежегодно изменяется в зависимости от
ставки рефинансирования ЦБ. После
каждого года сумма, равная процентному
приросту, добавляется к сумме счета.
Например, первоначальная сумма вклада
составила 100 денежных единиц. За первый
Вы получили 5% дохода по вкладу, за второй
7%, за третий 9% и за 4-й – 10%. Каков средний
уровень дохода по вкладу за 4 года?
Можно
сложить вычислить среднюю арифметическую
величину дохода:.
Верно ли это?
Ведем
следующие условные обозначения: P
– первоначальная сумма вклада,
— доход по вкладу в первый, второй, третий
и четвертый годы соответственно (в долях
единиц), F – сумма вклада по истечении
четырех лет.
Если
первоначальная сумма вклада — Р,
то после первого года она возрастает и
становится
.
В конце второго года эта сумма составит
.
В конце третьего года:.
По истечении четырех лет сумма составит
Если
необходимо определить средний процент
дохода i,
который даст сумму дохода F
по истечении четырех лет, при прибавлении
ежегодного накопленного прироста к
сумме вклада, то это будет величина,
которая определится из следующего
уравнения:
Решение этого
уравнения находится по формуле:
,
где (i+1)
— геометрическая средняя из (1+i1
),(1+i2),(1+i3),(1+i4)).
Средний
процент дохода по вкладу равен
,
что отличается от результата, полученного
по средней арифметической.
Общий вид формулы средней геометрической
невзвешенной:
Средней геометрической взвешенной:
(5.12)
Согласно правилу
мажорантности средней, расчет по средней
арифметической завышает результат, чем
длиннее период расчета, тем больше будет
ошибка.
Пример 2. В результате инфляции за
первый год цена товара возросла в два
раза к предыдущему году, а за второй год
еще в три раза к уровню предыдущего
года. Ясно, что за два года цена возросла
в 6 раз. Каков средний темп роста цены
за год? Арифметическая средняя здесь
непригодна, поскольку, если за год цена
выросла бы в (2+3)/2=2,5 раза, то за два года
цена выросла бы в 2,5 *2,5 = 6,25, а не в 6 раз.
Геометрическая средняя даст правильный
ответ:раза.
Геометрическая
средняя дает наиболее правильный по
содержанию результат осреднения, если
задача состоит в нахождении такого
значения признака, который качественно
был бы равно удален как от максимального,
так и от минимального значения признака.
Пример
3. Максимальный
выигрыш в лотерее составляет миллион
рублей, а минимальный – сто рублей.
Какую величину можно считать средней
между миллионом и сотней? Арифметическая
средняя явно непригодна, так как
составляет 500050 рублей, а это, как и
миллион, крупный, а никак не средний
выигрыш. Геометрическая средняя в этом
случае дает наиболее правильный с точки
зрения экономики и логики ответ:
руб.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Задача №6. Расчёт показателей вариации
- Определите:
- Решение:
- Задача по статистике S-15
- Номер задачи: S-15
- Решение: бесплатно
- По следующим данным о распределении 100 работников банка по величине месячной заработной платы определите среднюю заработную плату (используя способ моментов), приходящуюся на одного работника, моду и медиану.
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
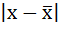 |
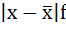 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
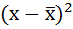 |
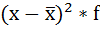 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Источник
Задача по статистике S-15


Номер задачи: S-15
Решение: бесплатно
По следующим данным о распределении 100 работников банка по величине месячной заработной платы определите среднюю заработную плату (используя способ моментов), приходящуюся на одного работника, моду и медиану.
| Группы работников по величине месячной заработной платы, долл. | Число рабочих, в процентах к итогу |
| 500-600 | 10 |
| 600-700 | 15 |
| 700-800 | 20 |
| 800-900 | 25 |
| 900-1000 | 15 |
| 1000-1100 | 10 |
| Более 1100 | 5 |
| Итого: | 100 |

Если Вы нашли, что искали, но решили набрать эту задачку самостоятельно, хочу немного облегчить Вам работу.
Ниже выкладываю «голый» текст задачи. Останется добавить формулы и графики.
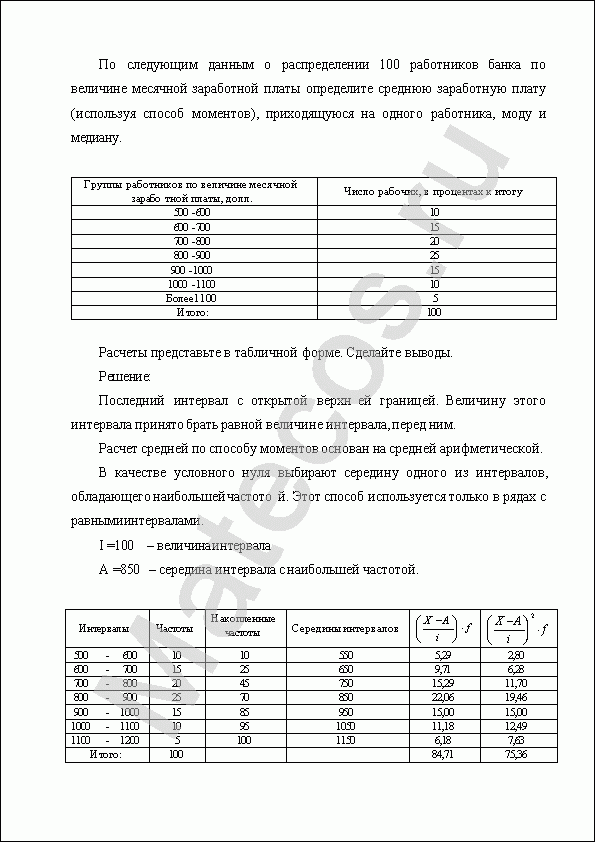
По следующим данным о распределении 100 работников банка по величине месячной заработной платы определите среднюю заработную плату (используя способ моментов), приходящуюся на одного работника, моду и медиану.
Группы работников по величине месячной заработной платы, долл.
Число рабочих, в процентах к итогу
Расчеты представьте в табличной форме. Сделайте выводы.
Последний интервал с открытой верхней границей. Величину этого интервала принято брать равной величине интервала, перед ним.
Расчет средней по способу моментов основан на средней арифметической.
В качестве условного нуля выбирают середину одного из интервалов, обладающего наибольшей частотой. Этот способ используется только в рядах с равными интервалами.
I = 100 – величина интервала
A = 850 – середина интервала с наибольшей частотой.
m1 — момент первого порядка,
m2 — момент второго порядка.
Среднее квадратическое отклонение свидетельствует о том, что рассматриваемая величина в среднем отклоняется от средней величины на 18,97.
Вычислим моду и медиану:
Мода – наиболее часто встречающееся значение признака в совокупности.
Для интервального ряда распределения, сразу можно указать только интервал, где будут находиться мода и медиана.
Для определения их величины используют формулы:
Медианным называется интервал, которому соответствует значение накопленной частоты большей полусуммы всех частот.
Источник
Adblock
detector