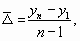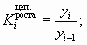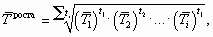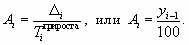Крайне неудобно анализировать множество значений за ряд периодов, поэтому целесообразнее вычислять средний показатель роста (убыли) определенного параметра. Средний темп роста является показателем статистической динамики для анализа явлений и процессов (интенсивности изменения и скорости роста) в различных областях жизнедеятельности: финансовой сфере, сфере производства и торговли, статического анализа и пр.
Коэффициент, отражающий средний за ряд периодов рост показателя в процентном измерении.
Структура формулы:
- значение на начало измерения;
- значение в конце измерения;
- промежуточные показания, через равные интервальные моменты.
T‾=n−1TсрT1100%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%
Tср=∑1nTkntext{Tср}=sum _1^n frac{T_k}{n}
где T1T_1 – начальное значение показателя,
TkT_k – значение показателя за период k(1…n)k (1…n),
nn – число периодов расчета,
Tсрtext{Tср} – среднее значение показателя.
Алгоритм расчета:
- Определение периода сравнения nn;
- Вычисление суммы параметров за период nn;
- Нахождение среднего параметра путем деления суммы (п.2) на число периодов nn;
- Вычисление среднего темпа роста как корень степени n−1n-1 от частного среднего и начального T$$ на 100%.100%.
Определить средний темп роста прибыли фирмы по следующим данным:
| Месяц | Сумма |
|---|---|
| Январь | 142000 руб. |
| Февраль | 146000 руб. |
| Март | 136000 руб. |
| Апрель | 151000 руб. |
| Май | 163000 руб. |
| Июнь | 113000 руб. |
| Июль | 122000 руб. |
| Август | 125000 руб. |
| Сентябрь | 132000 руб. |
| Октябрь | 156000 руб. |
| Ноябрь | 167000 руб. |
| Декабрь | 178000 руб. |
Решение
- Период n=12n = 12;
- Сумма прибыли за год:
142000+146000+136000+151000+163000+113000+122000+125000+132000+156000+167000+178000=1731000142000+146000+136000+151000+163000+113000+122000+125000+132000
+156000+167000+178000 = 1731000 руб.
- Средняя прибыль за год:
Tср=173100012=144250text{Tср}=173100012=144250руб.
- Средний темп роста:
T‾=14425014200011100%=1,00143⋅100%=100,143%overline{T}=sqrt[11]{frac{144250}{142000}}100%=1,00143cdot100%=100,143%
Ответ: Средний темп роста прибыли составил $100,143%$ в год.
Найти значение выручки в апреле, если известно, что в январе было заработано 6132 тыс. руб., в феврале – 5861 тыс. руб., в марте – 6318 тыс. руб. Показатель среднего темпа роста за 4 месяца — 113%.
Решение
- Средний темп роста
T‾=n−1TсрT1100%=113%overline {T}=^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}100%=113%
n−1TсрT1=1,13^{n-1} sqrt{frac{text{Tср}}{text{T}_1}}=1,13
4−1Tср6132=1,13^{4-1} sqrt{frac{text{Tср}}{6132}}=1,13
Tср6132=1,133frac{text{Tср}}{6132}=1,13^3
Tср6132=1,4429frac{text{Tср}}{6132}=1,4429
Tср=8847,86text{Tср}=8847,86 тыс. руб.
- Средняя выручка (XX – выручка за апрель):
Tср=∑1nTkn=8847,86text{Tср}=sum _1^n frac{T_k}{n}=8847,86
∑1nTk4=8847,86frac{sum_{1}^{n}T_k}{4}=8847,86
6132+5861+6318+X4=8847,866132+5861+6318+X4=8847,86
6132+5861+6318+X=35391,446132+5861+6318+X=35391,44
X=35391,44−6132−5861−6318=17080,44X=35391,44-6132-5861-6318=17080,44 тыс. руб.
Ответ: Выручка в апреле 17080,4417080,44 тыс. руб.
Средний темп роста является многогранным показателем, позволяющим наглядно отразить результаты изменения тех или иных экономических данных. По результатам анализа компания может оценить динамику роста, выявить влияющие факторы и спрогнозировать будущие показатели с учетом сезонных изменений.
Тест по теме «Формула среднего темпа роста»
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста
Средний уровень ряда в статистике
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
где у — абсолютные уровни ряда;
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
t1,… tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
где у1,…,уn — уровни периода, за который делается расчет;
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
где у1,…,уn — уровни рядов динамики;
t — интервал времени между смежными уровнями
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
где n — число степенных абсолютных приростов в исследуемом периоде.
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
где n — число цепных коэффициентов роста;
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Средний
абсолютный прирост (или средняя скорость
роста) —
средняя арифметическая из показателей
скорости роста за отдельные промежутки
времени.
Формула
расчета среднего абсолютного прироста:
где n —
число уровней ряда;
—
абсолютные изменения по сравнению с
предшествующим уровнем. Средний
абсолютный прирост показывает, на
сколько единиц увеличивался или
уменьшался уровень по сравнению с
предыдущим в среднем за единицу времени.
Характеризует среднюю абсолютную
скорость роста (или снижения) уровня,
является интервальным показателем,
вычисляя средний абсолютный прирост,
указывают:
1) за
какой календарный период исчислен
средний прирост;
2) в
расчете на какую единицу времени он
исчислен.
Средний
коэффициент роста —
показатель, вычисляемый по формуле
средней геометрической из показателей
коэффициентов роста за отдельные
периоды: ,
гдеK,K,…Kn-1, —
коэффициенты роста по сравнению с
уровнем предшествующего периода; n —
число уровней ряда.
Средний
темп роста
— средний коэффициент роста, выраженный
в процентах: Т
= К100
%, где K-.
средний годовой коэффициент роста.
Средний
темп прироста (или снижения),
выраженный 8 процентах, показывает, на
сколько процентов увеличивался (или
снижался) уровень по сравнению с
предыдущим в среднем за единицу времени.
Средний темп прироста характеризует
среднюю интенсивность роста.
Метод
расчета среднего уровня ряда
динамики зависит
от характера показателя, лежащего в
основе ряда, т. е. от вида временного
ряда:
1) средний
уровень интервального
ряда динамики абсолютных величин с
равностоящими уровнями рассчитывается
по формуле простой
средней
арифметической:
где n —
число фактических уровней за
последовательные равные отрезки времени;
2) средний
уровень интервального
ряда с разностоящими уровнями исчисляется
по формуле средней арифметической
взвешенной:
где t —
число периодов времени, в течение которых
уровень не изменялся;
3) средний
уровень моментного
ряда с равностоящими уровнями исчисляется
по формуле средней хронологической:
4) средний
уровень моментного ряда с разностоящими
уровнями исчисляется по формуле.
37. Статистика качества жизни населения: понятие, источники статистических данных.
Качество
жизни населения
— это степень удовлетворения материальных,
духовных и социальных потребностей
человека.
Качество жизни
населения напрямую зависит от ее уровня.
С ростом уровня жизни населения будет
расти доход населения, следовательно,
обеспеченность населения материальными
благами будет повышаться, и качество
жизни также будет расти.
Под
«качеством жизни» в широком смысле
понимается удовлетворенность населения
своей жизнью с точки зрения различных
потребностей и интересов.
Это понятие охватывает характеристики
и индикаторы уровня жизни как экономической
категории, условия труда и отдыха,
жилищные условия, социальную обеспеченность
и гарантии, охрану правопорядка и
соблюдение прав личности,
природно-климатические условия,
показатели сохранения окружающей среды,
наличие свободного времени и возможности
хорошо его использовать, наконец,
субъективные ощущения покоя, комфортности
и стабильности.
В
наше время даже без данных статистики
видно, что переход всей экономики нашей
страны на рыночные формы хозяйствования
совершается в основном за счет социальной
сферы, что наглядно проявляется в
ухудшении демографической ситуации и
падении уровня и качества жизни
большинства населения. Все больше людей
теряют здоровье, снижается основной
показатель страны, такой как рождаемость,
большими темпами сокращается
продолжительность жизни, но самое
главное – стареет население России, а
с ним и рабочая сила.
Это
просто объедение двух понятий.
Уровень
и качество жизни населения напрямую
зависит от возможностей людей удовлетворять
свои потребности, а как известно, для
удовлетворения постоянных первичных
потребностей человеку нужен постоянный
определенный доход. Основным доходом
населения Российской Федерации является
заработная плата.
Заработная
плата – составляющая дохода работника,
полученная им в ходе трудовой деятельности.
Помимо заработной платы уровень дохода
и качество жизни населения зависит от
социального обеспечения, доступности
материальных, духовных благ и услуг, а
также уровня образования основных масс
населения страны и др.
Применение
статистики в изучении уровня и качества
жизни населения позволяет решать
множество задач, главной из которых
является получение статистических
данных об уровне и качестве жизни
населения с целью их повышения.
Перед
статистикой уровня жизни населения
стоят следующие задачи:
-
разработка
системы показателей, объективно,
достоверно и всестороннее характеризующих
уровень и качество жизни населения; -
статистический
анализ динамики уровня и качества жизни
населения; -
выявление
обстоятельств, оказывающих влияние на
изменение уровня и качества жизни
населения; -
определение
основных тенденций и закономерностей
изменения уровня и качества жизни
населения; -
анализ
разрозненности показателей уровня и
качества жизни населения по регионам; -
определение
уровня удовлетворения потребностей
жителей страны в материальных ресурсах
и услугах по сопоставлению с установленными
нормами потребления; -
усовершенствование
системы источников для сбора статистической
информации об уровне и качестве жизни
населения; -
определение
показателей уровня и качества жизни
населения, которые будут связаны между
собой.
Для
решения последней задачи в 1992 г. в
Центре экономической конъюнктуры и
прогнозирования была предложена система
основных показателей уровня жизни
населения:
-
обобщающие
показатели; -
доходы
населения; -
потребление
и расходы населения; -
денежные
сбережения населения; -
накопленное
имущество и жилище; -
социальная
дифференциация населения; -
малообеспеченные
слои населения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
9.2. Показатели ряда динамики
При анализе динамического ряда рассчитываются следующие показатели:
- средний уровень динамического ряда;
- абсолютные приросты: цепные и базисные, средний абсолютный прирост;
- темпы роста: цепные и базисные, средний темп роста;
- темпы прироста: цепные и базисные, средний темп прироста;
- абсолютное значение одного процента прироста.
Цепные и базисные показатели вычисляются для характеристики изменения уровней динамического ряда и различаются между собой базами сравнения: цепные рассчитываются по отношению к предыдущему уровню (переменная база сравнения), базисные — к уровню, принятому за базу сравнения (постоянная база сравнения).
Средние показатели представляют собой обобщенные характеристики ряда динамики. С их помощью сравнивают интенсивность развития явления по отношению к различным объектам, например по странам, отраслям, предприятиям и т.д., или периодам времени.
9.2.1. Средний уровень ряда динамики
Конкретное числовое значение статистического показателя, относящееся к моменту или периоду времени, называется уровнем ряда динамики и обозначается через yi (где i — показатель времени).
Методика расчета среднего уровня зависит от вида динамического ряда, а именно: является ли он моментным или интервальным, с равными или неравными временными промежутками между соседними датами.
Если дан интервальный ряд динамики абсолютных или средних величин с равными периодами времени, то для расчета среднего уровня применяется формула средней арифметической простой:
где y1, y2, yi, …, yn — уровни динамического ряда;
п — число уровней ряда.
Пример 9.2. По данным таблицы определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект за полугодие:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб | 106 | 108 | 108 | 111 | 110 | 112 |
Если временные промежутки интервального динамического ряда неравны, то значение среднего уровня находят по формуле средней арифметической взвешенной, в которой в качестве весов используют длину временных периодов, соответствующих уровням ряда динамики (ti)
Пример 9.3. По данным, представленным в таблице, определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект:
| Месяц | Январь | Февраль | Март | II квартал | III квартал | IV квартал |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб. | 106 | 110 | 138 | 150 | 160 | 140 |
В моментных рядах динамики с одинаковыми временными промежутками между датами средний уровень ряда рассчитывается по формуле средней хронологической простой
где yn — значения показателя на конец рассматриваемого периода.
Пример 9.4. По приведенным ниже данным о размере денежных средств на счете вкладчика на начало каждого месяца определим средний размер вклада в I квартале 2006 г.:
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.04.06 |
|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 000 | 147 289 | 151 870 | 148 500 |
Средний уровень моментного ряда динамики равен:
Хотя I квартал включает три месяца (январь, февраль, март), в расчете должны быть использованы четыре уровня ряда (включая данные на 1 апреля). Это легко доказать. Действительно, если исчислять средние уровни по месяцам, то получим:
в январе
в феврале
в марте
Рассчитанные средние образуют интервальный ряд динамики с равными временными промежутками, в котором средний уровень исчисляется, как мы видели выше, по формуле средней арифметической простой:
Аналогично, если требуется рассчитать средний уровень моментного ряда динамики с равными интервалами между датами за первое полугодие, то в качестве последнего уровня в формуле средней хронологической простой следует взять данные на 1 июля, а если за год — данные на 1 января следующего года.
В моментных рядах динамики с неравными промежутками между датами для определения среднего уровня применяется формула средней хронологической взвешенной:
где ti — длина временного периода между двумя соседними датами.
Пример 9.5. По данным о запасах товаров на начало месяца определим средний размер товарных запасов в 2006 г.
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.07.06 | 01.09.06 | 01.12.06 | 01.01.07 |
|---|---|---|---|---|---|---|---|
| Запасы товаров, тыс. руб. | 1 320 | 1 472 | 1 518 | 1 300 | 1 100 | 1 005 | 920 |
Средний уровень ряда равен:
Расстояние между датами
Если имеется полная информация о значениях моментного статистического показателя на каждую дату, то среднее значение этого показателя за весь период исчисляется по формуле средней арифметической взвешенной:
где yi — значения показателя
ti — длина периода, в течение которого это значение статистического показателя оставалось неизменным.
Если мы дополним пример 9.4 информацией о датах изменения денежных средств на счете вкладчика в I квартале 2006 г., то получим:
- остаток денежных средств на 1 января — 132 000 руб.;
- января выдано — 19 711 руб.;
- 28 января внесено — 35 000 руб.;
- 20 февраля внесено — 2000 руб.;
- 24 февраля внесено — 2581 руб.;
- 3 марта выдано — 3370 руб. (в марте других изменений не происходило).
Итак, с 1 по 4 января (четыре дня) значение показателя оставалось равным 132 000 руб., с 5 по 27 января (23 дня) его значение составило 112 289 руб., с 28 января по 19 февраля (23 дня) — 147 289 руб., с 20 по 23 февраля (четыре дня) — 149 289 руб., с 24 февраля по 2 марта (семь дней) — 151 870 руб., с 3 по 31 марта (29 дней) — 148 500 руб. Для удобства проведения расчетов представим эти данные в таблице:
| Длина периода, дней | 4 | 23 | 23 | 4 | 7 | 29 |
|---|---|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 00 | 112 289 | 147 289 | 149 289 | 151 879 | 148 500 |
По формуле средней арифметической взвешенной находим значение среднего уровня ряда
Как видим, среднее значение отличается от полученного в примере 9.4, оно является более точным, так как в вычислениях использовалась более точная информация. В примере 9.4 были известны лишь данные на начало каждого месяца, при этом не оговаривалось, когда же именно происходили изменения показателя, была применена формула хронологической средней.
В заключение отметим, что расчет среднего уровня ряда теряет свой аналитический смысл в случаях большой изменяемости показателя внутри ряда, а также при резкой смене направления развития явления.
9.2.2. Показатели абсолютного изменения уровней динамического ряда
Абсолютные приросты рассчитываются как разность между двумя значениями соседних уровней динамического ряда (цепные приросты) или как разность между значениями текущего уровня и уровня, принятого за базу сравнения (базисные приросты). Показатели абсолютного прироста имеют те же единицы измерения, что и уровни динамического ряда. Они показывают, на сколько единиц изменился показатель при переходе от одного момента или периода времени к другому.
Базисные абсолютные приросты рассчитывают по формуле
где уi — i-й текущий уровень ряда,
y1 — первый уровень ряда динамики, принятый за базу сравнения.
Формула для определения цепных абсолютных приростов имеет вид
где уi — 1 — уровень, предшествующий i-му уровню динамического ряда.
Средний абсолютный прирост показывает, на сколько единиц в среднем ежемесячно, или ежеквартально, или ежегодно и т.д. изменялось значение показателя в течение рассматриваемого периода времени. В зависимости от того, какими данными мы располагаем, его можно рассчитать следующими способами:
-
— цепные абсолютные приросты показателя;
-
где yn — последний уровень ряда
Пример 9.6. По данным таблицы определим показатели абсолютных приростов размера страхового возмещения, выплаченного страховой компанией.
 |
* Сумма всех рассчитанных цепных абсолютных приростов дает базисный абсолютный прирост последнего периода.
Среднемесячный абсолютный прирост за полугодие равен
Таким образом, в среднем ежемесячно размер выплат страхового возмещения увеличивался на 1,2 тыс. руб.
9.2.3. Показатели относительного изменения уровней динамического ряда
Характеристиками относительного изменения уровней ряда динамики являются коэффициенты и темпы роста значений показателя и темпы их прироста.
Коэффициент роста представляет собой соотношение двух уровней динамического ряда, выраженное в виде простого кратного отношения. Он показывает, во сколько раз изменилось значение показателя в одном периоде (моменте) времени по сравнению с другим. Темп роста — это коэффициент роста, выраженный в процентах. Он показывает, сколько процентов составляет значение показателя в данном периоде, если уровень, с которым проводится сравнение, принять за 100%.
Так же, как и абсолютные приросты, коэффициенты и темпы роста могут быть цепными и базисными.
Цепные коэффициент и темп роста измеряют относительное изменение текущего уровня показателя по сравнению с предшествующим ему уровнем:
коэффициент роста:
темп роста:
Базисные коэффициент и темп роста характеризуют относительное изменение текущего уровня показателя по сравнению с базисным (чаще всего с первым) уровнем:
коэффициент роста
темп роста
Цепные и базисные коэффициенты роста имеют между собой следующую связь:
- произведение всех рассчитанных до текущего периода цепных коэффициентов роста дает базисный коэффициент роста текущего периода:
- деление базисного коэффициента роста текущего периода на базисный коэффициент роста предшествующего периода дает цепной коэффициент роста текущего периода:
Средние темп роста и коэффициент роста в динамических рядах с равноотстоящими уровнями рассчитываются по формуле средней геометрической простой


Эти формулы могут быть приведены к следующему виду:
Для того чтобы определить, на сколько процентов текущий уровень показателя больше или меньше значения предшествующего или базисного уровня, рассчитываются темпы прироста. Они исчисляют путем вычитания 100% из соответствующих темпов роста:
Средний темп прироста рассчитывается аналогичным образом: из среднего темпа роста вычитаются 100%:
Пример 9.7. В таблице приведены рассчитанные коэффициенты роста, темпы роста и прироста показателя, характеризующего среднемесячный размер выплаченного компанией страхового возмещения за период с января по июнь.
| Месяц | Средний размер выплаченного страхового возмещения, тыс. руб., yi | Коэффициент роста | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. руб. | |||
|---|---|---|---|---|---|---|---|---|
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| Январь | 106 | — | 1 | — | 100 | — | — | — |
| Февраль | 108 | 1,019 | 1,019 | 101,9 | 101,9 | 1,9 | 1,9 | 1,06 |
| Март | 108 | 1,000 | 1,000 | 100,0 | 101,9 | 0 | 1,9 | 1,08 |
| Апрель | 111 | 1,028 | 1,047 | 102,8 | 104,7 | 2,8 | 4,7 | 1,08 |
| Май | 110 | 0,991 | 1,038 | 99,1 | 103,8 | -0,9 | 3,8 | 1,11 |
| Июнь | 112 | 1,018 | 1,057 | 101,8 | 105,7 | 1,8 | 5,7 | 1,10 |
По формуле средней геометрической простой определим среднемесячный коэффициент роста показателя за период с февраля по июнь:
или
Средний темп роста, соответственно, равен 101,1%. Следовательно, в среднем ежемесячно размер выплат страхового возмещения увеличивался в 1,011 раза, или на 1,1%.
Если известны средние темпы (или коэффициенты) роста за некоторые неравные отрезки времени, то средний темп роста за весь период исчисляется по формуле средней геометрической взвешенной:
где Тi — средний темп роста за i-й период времени;
ti — длина i-го периода.
Пример 9.8. Среднегодовые коэффициенты роста числа страховых компаний в одной из областей России составили за период 1991-1995 гг. — 1,18; 1995-2000 гг. — 1,24; 2000-2004 — 1,56. Определим среднегодовой коэффициент роста числа страховых компаний за весь период с 1991 по 2004 гг.
Решение:
Таким образом, за период с 1991 по 2004 гг. среднегодовой темп роста числа страховых компаний в одной из областей России составил 131,1%, соответственно, среднегодовой темп прироста — 31,1%.
Для более полного анализа динамики расчет цепных показателей роста и прироста уровней динамического ряда часто сопровождаются указаниями абсолютных значений 1% прироста.
Абсолютное значение 1% прироста (Аi) определяется как отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени:
В последней графе таблицы примера 9.7 рассчитаны цепные абсолютные значения 1% прироста.

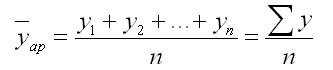
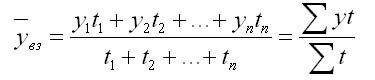
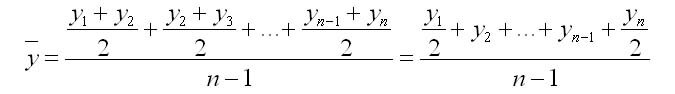
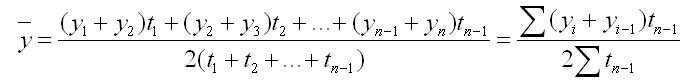
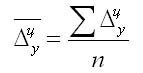
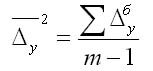
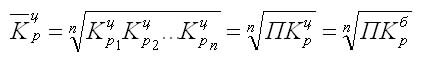
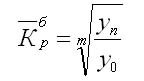
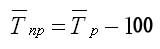
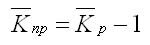






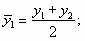






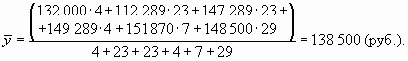

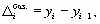

 — цепные абсолютные приросты показателя;
— цепные абсолютные приросты показателя;