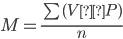Как найти среднее значение признака биология - AvtoShod.ru

Среднее значение признака и методы вычисления этой величины

Полученные
при обследовании значения признаков
характеризуют каждую конкретную особь
в отдельности. Общие свойства совокупности
оценивают с помощью средней величины,
которую обозначают в биометрии буквой
M или
.
Этот показатель используется для
характеристики однородных групп
животных по какому-либо признаку,
сравнения отдельных стад и пород, оценки
предприятий, хозяйств и конкретных
специалистов. Так, например, если в одном
хозяйстве средний удой на корову
составляет 3000 кг, а в другом — 4000 кг, то
по среднему значению признака видно,
где лучше стадо.

Различают
несколько методов вычисления средней
арифметической величины. Наиболее
простой, который используют в основном
для малых выборок — метод
суммирования:
складывают все значения вариант и делят
их

сумму
на объем выборки. В математическом
выражении это выглядит так:

∑V
где ∑ — знак суммирования,

M
= ─── ; V — значения вариант,

n
n — объем выборки.

Для
примера найдем с помощью этого метода
среднюю живую массу 10 гусей, кг: 5,6
7,0 6,3 7,4 8,0 6,7 6,4 6,9 6,1 6,8

5,6
+ 7,0 + 6,3 + 7,4 + 8,0 + 6,7 + 6,4 + 6,9 + 6,1 + 6,8 67,1

M
= ────────────────────────────────
= ─── = 6,71 кг.

10
10

В
случаях, когда значения признака имеют
разные частоты (вес) или в каждой группе
уже известны средние показатели, среднюю
арифметическую величину определяют
методом
взвешивания:
каждое значение признака умножают на
его частоту, полученные произведения
суммируют и делят на объем выборки.
Среднюю взвешенную величину вычисляют
по формуле:

p₁V₁
+ p₂V₂
+ p_nV_n
∑рV где М — средняя взвешенная,

M
= ───────────── = ────; p
— частоты,

p₁
+ p₂
+ p_n
∑p V — варианты.

Для
примера вычислим этим методом среднюю
жирность молока коровы Зорьки за лактацию
(табл.3).

3.
Продуктивность коровы Зорька по месяцам
лактации

Месяцы

Удой,
кг (р)

Жирность

молока,
%

1%
молоко, кг

(рV)

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

Январь

247

621

720

723

608

510

501

435

434

170

∑р
= 4969

3,6

3,4

3,6

3,5

3,8

3,7

4,0

4,2

889

2226

2448

2603

2222

1938

1854

1609

1736

714

∑рV
= 18156

В
этом примере за конкретное значение
признака (V) взят процент жира в молоке
коров, а за частоту (р) — месячный удой.

∑рV
18155

M
= ──── = ──── = 3,65(%)

∑р
4969

При
группировке цифрового материала в
вариационный ряд среднюю арифметическую
величину удобно вычислять методом
условных отклонений по
формуле:

∑рa
где A — условно среднее
значение

M
= A + i ──── ; i — классовый интервал

n
р — частота, а — условное откл.

n
— объем выборки

Используя
этот метод, вычислим среднюю длину
шерсти овец породы прекос по следующим
данным: (см)

7,5
8,5 8,0 8,0 9,0 10,0 8,5 10,0 7,0 6,0 7,5 9,0
10,0 8,0

9,0
10,0 7,0 9,5 8,5 8,0 10,0 7,5 8,5 9,0 8,0 9,5
8,5 8,0

10,0
12,0 11,0 9,0 8,5 8,0 8,5 9,0 11,0 7,0 9,0 8,5

n
= 40

Для
построения вариационного ряда находим
минимальное и макси-мальное значения
признака, определяем лимит, устанавливаем
число классов и величину классового
промежутка.

1.
min
= 6,0; max
= 12,0; lim
= 12,0 — 6,0 = 6,0

2.
Число классов — 6

lim
6,0

3.
Классовый промежуток i = ──────────
= ─── = 1,0 (см).

число
классов 6

Схема
расчета приведена в таблице 4.

4.
Алгоритм вычисления средней арифметической
величины методом условных отклонений

Границы
классов

(
Vн. — Vк.)

Средние
знач.

класса
(Vср.)

Частота

(р)

Условные
откл. (а)

р×а

6,0
– 6,9

7,0
– 7,9

А
8,0
– 8,9

9,0
– 9,9

10,0
– 10,9

11,0
– 12,0

6,5

7,5

8,5

9,5

10,5

11,5

n=40

-2

-1

-2

-6

∑рa
= 22

После
построения вариационного ряда выделяем
условно среднее значение признака — A.
Обычно это среднее значение класса с
максимальной частотой. В нашем примере
A = 8,5. Затем проставляем условные
отклонения (а), которые показывают, на
сколько классовых промежутков каждый
из классов отклоняется от условно
среднего или нулевого класса. Вверх от
нулевого идут отрицательные отклонения,
вниз — положительные. После заполнения
таблицы находим для каждого класса
произведение частот (р) на отклонения
(а) и их сумму ( ∑ра). Теперь по формуле
находим среднее значение признака:

∑рa
22

М
= A
+ i
───── = 8,5 + 1,0 ─── = 9,05 (см)

n
40

Кроме
средней арифметической величины
среднее значение признака характеризуют
средняя геометрическая (G), средняя
квадратическая (S), средняя гармоническая
(H), мода (Мо) и медиана (Ме). Сведения об
этих величинах и их использовании можно
найти в специальной литературе по
биометрии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

ЛАБОРАТОРНАЯ
РАБОТА № 2

Выявление
изменчивости организмов.

Цель:
познакомить учащихся с модификационной изменчивостью и ее

статистическими
закономерностями, выработать умение строить вариационный ряд, вариационную
кривую и находить среднюю величину признака

Ход
работы.

·
выполните задания, предложенные вам на
карточке

Оформление
результатов:

·
полученные данные занесите в таблицу

·
вычислите среднюю величину признака:

Σ
(v p)

M = ————,

где
M
– средняя величина признака

n
— общее число вариант

·
начертите вариационную кривую

Сделайте вывод о
том,

какая
закономерность модификационной изменчивости вами обнаружена.

Задания на карточках:

Задание
1. Измерили рост учеников в 3-б классе, значение (в см) получились

следующие

110, 115, 112,
115, 114, 112, 113, 110, 113, 115, 112, 110, 115, 112, 110.

Составьте
вариационный ряд, начертите вариационную кривую, найдите среднюю величину
признака.

Задание
2. Определили массу учеников в 3-б классе, значение (в см)

Получились следующие

25, 27, 24, 30,
26, 25, 26, 25, 24, 30, 24, 24, 26, 26, 27.

Составьте
вариационный ряд, начертите вариационную кривую, найдите среднюю величину
признака

Изучение
модификационной изменчивости у растений, построение вариационного ряда и кривой

[ ]

09.05.2010,
11:27

Лабораторная
работа
(к теме «Основы генетики»)

Изучение модификационной
изменчивости у растений, построение вариационного ряда и кривой

Цель: показать статистические
закономерности модификационной изменчивости на примере использования
математических методов в биологии.

Оборудование: клубни картофеля,
линейка, простой карандаш.

Ход работы:
Построение вариационного ряда и кривой изменчивости количества почек-глазков
на клубнях картофеля.
1. Подсчитайте количество почек-глазков на клубнях картофеля (10).
2. Расположите их в порядке нарастания величины данного признака, обозначьте
цифрами наиболее часто встречающиеся величины признака получите вариационный
ряд.
3. запишите полученные данные вариационного ряда в таблицу:
N V P E M

Где N – общее число вариант вариационного ряда;
V – варианта;
P – частота встречаемости вариант;
E – знак суммирования;
M – средняя величина признака.
4. Постройте графическое выражение (вариационную кривую) изменчивости
признака – количество почек-глазков на клубнях картофеля.
С этой целью:
— по оси абсцисс отложите на одинаковом расстоянии отдельные варианты
количество почек-глазков на клубнях картофеля в нарастающем порядке;
— по оси ординат отложите числовые значения, соответствующие частоте
повторяемости каждой варианты (количество почек-глазков на клубнях
картофеля);
— по горизонтальной оси восстановите перпендикуляры до уровня,
соответствующего частоте повторяемости каждой варианты;
— точки пересечения перпендикуляров с линиями, соответствующими частоте
вариант, соедините прямыми.
5. определите среднюю величину указанного признака — количество почек-глазков
на клубнях картофеля, используя для этой цели формулу:

M = Е (V Р) / N
6. Проведите сравнение цифровых данных вариационной кривой и сделайте вывод о
частоте встречаемости почек-глазков определенного количества.

Ответьте на вопросы:

1. Как называется полученная вами
линия?
2. С каким числом почек-глазков наиболее часто встречаются клубни?
Выводы:
1. Длина вариационного ряда свидетельствует о …
2. Графическим выражением модификационной изменчивости признака является…
3. Пределы вариационной изменчивости признака ограничены…
Ответы на вопросы:

1. Как называется полученная вами
линия? (вариационная кривая признака – числа почек-глазков на клубне
картофеля)
2. С каким числом почек-глазков наиболее часто встречаются клубни картофеля?

Выводы:
1. Длина вариационного ряда свидетельствует о разнообразии условий среды –
чем разнообразнее условия среды, тем шире модификационная изменчивость.
2. Графическим выражением модификационной изменчивости признака является
вариационная кривая.
3. Пределы вариационной изменчивости признака ограничены генотипом и
передаются по наследству.

Цель:

Ознакомиться с
явлением модификационной изменчивости и его статистическими закономерностями,
выработать умение строить вариационный ряд и график изменчивости изучаемого
признака.

Ход работы:

1. Определение явления
изменчивости.

1.1. Рассмотреть предлагаемые
изображения листьев определенного растения (шелковицы). Определить особенности
их строения, характерные для всех экземпляров, а также те, которыми они
различаются между собой.

1.2. Определить какие признаки из
приведенных в таблице являются характерными для всех изученных объектов
(неизменяемые признаки), а ка-кими они различаются между собой (изменяемые
признаки).

2. Построение вариационной кривой.

2.1. Подсчитать число случаев
встречи определенного значения ширины листовой пластинки березы (результаты
измерений находятся в прилагаемой таблице). При этом результаты измерений
должны быть объединены в клас-сы шириной два миллиметра.

2.2. Рассмотреть и проанализировать
график, построенный по результатам проведенных измерений. Сделать вывод о
статистических закономерностях изменчивости.

3. Построение вариационной кривой
по антропометрическим данным.

3.1. Ученики выбирают под контролем
учителя или без него некоторые ко-личественные признаки внешнего строения
человека (например, рост) и проводят измерения этих признаков у одноклассников.
Возможен выбор раз-ных признаков для разных учеников, на усмотрение учителя.

3.2. Результаты проведенных
измерений вносятся в предлагаемую сценари-ем таблицу.

3.3. По введенным данным строится
вариационная кривая. Необходимо про-анализировать, соответствует ли
закономерность распределения выбранного признака закономерности, выявленной в
предыдущей части работы.

4. Сделать общий вывод о
изменчивости и ее закономерностях.

Работа
рекомендуется для индивидуального выполнения. Возможен режим группового
выполнения при демонстрации через проектор с комментариями учителем хода
выполнения.

Модификационная изменчивость многих признаков растений, животных и
человека подчиняется общим закономерностям. Эти закономерности выявляются на
основании анализа проявления признака у группы особей (n). Степень выраженности
изучаемого признака у членов выборочной совокупности различна. Каждое
конкретное значение изучаемого признака называют вариантой и
обозначают буквой v. Частота встречаемости отдельных вариант
обозначается буквой p. При изучении изменчивости признака в
выборочной совокупности составляется вариационный ряд, в котором особи
располагаются по возрастанию показателя изучаемого признака.

Например, если взять 100 колосьев пшеницы (n = 100),
подсчитать число колосков в колосе (v) и число колосьев с данным
количеством колосков, то вариационный ряд будет выглядеть следующим образом.

Варианта (v)	14	15	16	17	18	19	20
Частота встречаемости (p)	2	7	22	32	24	8	5

Вариационная кривая

На основании вариационного ряда строится вариационная
кривая — графическое отображение частоты
встречаемости каждой варианты.

Среднее значение признака встречается чаще, а вариации,
значительно отличающиеся от него, — реже. Это называется «нормальным
распределением». Кривая на графике
бывает, как правило, симметричной.

Среднее значение признака подсчитывается по формуле:

где М — средняя величина признака; ∑(v·p)
— сумма произведений вариант на их частоту встречаемости; n —
количество вариант.

В данном примере среднее значение признака (числа колосков в
колосе) равно 17,13.

Знание закономерностей модификационной изменчивости имеет большое
практическое значение, поскольку позволяет предвидеть и заранее планировать
степень выраженности многих признаков организмов в зависимости от условий
внешней среды.

Источник

A stem-and-leaf plot is a type of plot that displays data by splitting up each value in a dataset into a stem and a leaf.

This tutorial explains how to calculate the mean, median, and mode of a stem-and-leaf plot.

Example: Mean, Median & Mode of Stem-and-Leaf Plot

Suppose we have the following stem-and-leaf plot that shows the height of 19 different plants:

Mean:

To find the mean of this dataset, we can add up all of the individual values and divide by the total sample size of 19:

Mean = (11+12+13+26+26+30+31+31+42+45+46+51+52+61+78+82+82+93+94) / 19 = 47.68.

The mean turns out to be 47.68. This is the average value of the dataset.

Median:

To find the median of this dataset, we can write out all of the individual values in order and identify the value that lies directly in the middle:

11, 12, 13, 26, 26, 30, 31, 31, 42, 45, 46, 51, 52, 61, 78, 82, 82, 93, 94

The median turns out to be 45. This is the value located directly in the middle of the dataset.

Mode:

To find the mode of this dataset, we can identify the values that occur most often:

11, 12, 13, 26, 26, 30, 31, 31, 42, 45, 46, 51, 52, 61, 78, 82, 82, 93, 94

This dataset has two modes: 26 and 82. Each of these values occurs twice in the dataset while every other value only occurs once.

Additional Resources

Stem and Leaf Plot Generator
How to Create a Stem-and-Leaf Plot in Excel
How to Create Back to Back Stem-and-Leaf Plots
How to Make a Stem and Leaf Plot with Decimals

Источник

Помогите рассчитать среднюю величину выраженности по формуле M = V * P / n, где М — средняя величина , V — размер, P — частота встречаемости 1)Надо подставить вот это : (РАЗМЕР СЕМЕЧКИ)1, 1 (32)(КОЛ — ВО) 0, 9 (9) 1, 4 : (6) 1, 2 (21) 1, 3(16) 1, 5(1) 1, 0(13) 0, 8(2) 2)Построить вариационную кривую кто разбирается помогите.

На этой странице сайта размещен вопрос Помогите рассчитать среднюю величину выраженности по формуле M = V * P / n, где М — средняя величина , V — размер, P — частота встречаемости 1)Надо подставить вот это : (РАЗМЕР СЕМЕЧКИ)1, 1 (32)(КОЛ -? из категории
Биология с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.

Источник

Пример выполненной лабораторной работы № 3

«Изучение изменчивости. Построение вариационного ряда и кривой».

Цель: познакомиться с закономерностями модификационной изменчивости, выработать умения строить вариационный ряд и график изменчивости изучаемого признака; вычислять среднюю величину признака, определять норму реакции

Оборудование: ростомер, рулетка, карандаш, линейка

Ход работы:

Измерьте рост каждого школьника в классе с точностью до сантиметра, округлив цифры.
Расположите данные в порядке нарастания величины признака, получите вариационный ряд и запишите данные вариационного ряда в таблицу.

Каждое конкретное значение изучаемого признака называют вариантой V

Таблица № 1

№

Vвариант
(рост
см)

Сгруппируйте полученные цифры, которые отличаются друг от друга на 5 см. (например, 150-155 см, 156-160 см, 161-165 см. ).

Подсчитайте количество учеников входящих в каждую группу и заполните таблицу.

Частота встречаемости отдельных вариант обозначается буквой P

Таблица № 2

V варианта рост (см) 150 -155 156 -160 161 -165 166 -170 171 -175 176 — 180 181 -186

Р частота встречаемости
(количество учащихся)

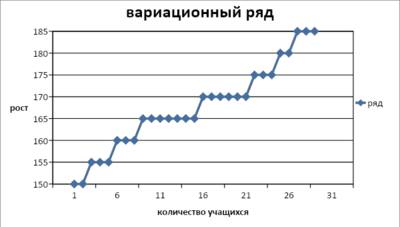
5. Постройте вариационный ряд.

С этой целью:

— по оси абсцисс отложите на одинаковом расстоянии количество учащихся;

— по оси ординат отложите числовые значения признака (рост)

Пример:

6. Постройте вариационную кривую

На основании вариационного ряда строится вариационная кривая — графическое отображение частоты встречаемости каждой варианты.

С этой целью:
— по оси абсцисс отложите на одинаковом расстоянии отдельные варианты роста в нарастающем порядке;
— по оси ординат отложите числовые значения, соответствующие частоте повторяемости каждой варианты

Пример:

7. Вычислите среднюю величину признака (средний рост учеников).

Среднее значение признака встречается чаще, а вариации, значительно отличающиеся от него, — значительно реже. Это называется нормальным распределением.

M – среднее значение признака

V – значение варианты

P – частота встречаемости варианты

n – общее число вариант вариационного ряда

8. Определите норму реакции и широту нормы реакции.

Норма реакции ________

Определите широту нормы реакции для этого из максимального значения признака вычислите минимальное.

max-min= __________

Выводы:

1. Длина вариационного ряда свидетельствует о …………………………………………………………………………………………………

2. Графическим выражением модификационной изменчивости признака является……………………………………………………………………

3. Пределы вариационной изменчивости признака ограничены……………………………………………………………………………………………..

Источник

V варианта рост (см)	150 -155	156 -160	161 -165	166 -170	171 -175	176 — 180	181 -186
Р частота встречаемости (количество учащихся)

Среднее значение признака и методы вычисления этой величины

Example: Mean, Median & Mode of Stem-and-Leaf Plot

Additional Resources

Не пропустите также: