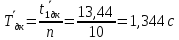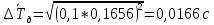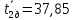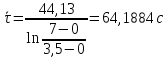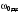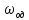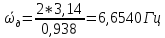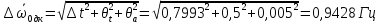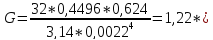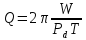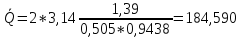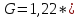В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F — частота (Гц) , v — скорость распространения колебаний в среде (м/с) , λ — длина волны (м) .
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T — период колебаний (с) , F — частота (Гц) .
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F — частота (Гц) , T — период колебаний (с) .
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω — циклическая частота (радиан в секунду) , F — обычная частота (Гц)
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F — обычная частота (Гц) , ω — циклическая частота (радиан в секунду) .
Задание по обработке
результатов
-
Статистическая обработка измеренных
значений. Определить по данным
таблиц 1 и 2 средние значения интервалов
времени
,
,
и
.
Определить погрешности этих величин
с доверительной вероятностью P
= 95%.
Таблица 1
|
N |
1 |
2 |
3 |
4 |
5 |
|
|
9,51 |
9,35 |
9,51 |
9,33 |
9,49 |
|
|
13,53 |
13,3 |
13,29 |
13,56 |
13,52 |
|
|
37,76 |
39,21 |
37,28 |
38,37 |
37,85 |
|
|
44,3 |
44,82 |
45,32 |
44,13 |
43,89 |
Определим средние значения



Формула расчета СКО
Формула случайной доверительной
погрешности результата измерений
Приборная погрешность
Полные погрешности результатов измерений
вычисляются по формуле
и равны:
Значит,

равны:
с
Сведем все вычисленные значения в
Таблицу 2
Таблица 2
|
Среднее |
Результат, |
|
|
|
|
|
|
|
|
|
|
|
|
-
Определение периода колебаний
маятника. Пользуясь методом
переноса погрешностей, для диска без
кольца и с кольцом рассчитайте средние
значения и полные погрешности периода
колебаний
.
Проведем расчеты для диска без кольца:
Расчетная формула

где n=10.
Пользуясь значениями, найденными в
пункте 1 (Таблица 2), вычислим
Полная погрешность
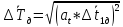
где
Значит, среднее значение периода
колебания диска без кольца

а полная погрешность периода колебаний
составляет 0,0015 с
с
Проведем расчеты для диска с кольцом:
Расчетная формула

где n=10.
Пользуясь значениями, найденными в
пункте 1 (Таблица 2), вычислим
Полная погрешность

где
Значит, среднее значение периода
колебания диска с кольцом
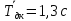
а полная погрешность периода колебаний
составляет 0,2 с.
3. Определение момента инерции
маятника. Определить момент
инерции маятника по формуле
,

где
– момент инерции кольца. Вычислить
погрешность
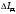
пользуясь правилами расчета погрешностей
косвенных измерений. Рассчитать значение
момента инерции диска маятника, исходя
из его размеров и плотности материала.
Сравнить полученный результат с
экспериментальным значением.
Пользуясь расчетами пунктов 1 и 2 определим
среднее значение момента инерции
маятника

которое рассчитывается по формуле
Погрешность измерений момента инерции
равна

Произведем расчет инерции диска маятника,
исходя из его размеров и плотности
материала. Расчетная формула

где
– плотность материала,
— толщина диска маятника,
— диаметр диска маятника
4. Определение времени затухания
маятника. Пользуясь методом
переноса погрешностей, для диска без
кольца и с кольцом рассчитайте средние
значения и полные погрешности времени
затухания
маятника и погрешность
при P = 95%. Время
затухания вычисляется по формуле

Определим время затухания маятника
без кольца
Воспользуемся значениями
и

расчитаными в пункте 1 (Таблица 2)
Рассчитаем среднее значение времени
затухания маятника
Полная погрешность времени затухания
маятника без кольца вычисляется по
формуле
Значит, время затухания маятника без
кольца равно
с
Определим время затухания маятника
с кольцом
Воспользуемся значениями
и

расчитаными в пункте 1 (Таблица 2)
Рассчитаем среднее значение времени
затухания маятника
Полная погрешность времени затухания
маятника с кольцом вычисляется по
формуле
Значит, время затухания маятника с
кольцом равно

5. Определение собственной частоты
колебаний гармонического осциллятора.
Пользуясь выражениями
и
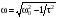
определить собственные частоты
и
колебаний для диска без кольца и с
кольцом. Вычислить их погрешности.
Собственные частоты
и
можно вычислить по формуле

6,6539 Гц

4,6726 Гц
Погрешность
Погрешность
6. Определение коэффициента
кручения и модуля сдвига материала
подвеса. Найти коэффициент кручения
и погрешность k.
Рассчитать среднее значение модуля
сдвига G.
Коэффициент кручения можно рассчитать
по формуле
Рассчитаем модуль сдвига

где l – длина подвеса,
а d – диаметр подвеса
1011 1/м3
7. Определение полной энергии,
мощности потерь и добротности маятника.
Пользуясь соответствующими
соотношениями, определить средние
значения указанных величин.
Полная энергия маятника W
рассчитывается по формуле
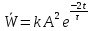
где A – конечная амплитуда
Мощность потерь
расчитывается по формуле
Добротность маятника
расчитывается по формуле
Дж
8. В соответствии с уравнением
затухающих колебаний построить графики
зависимости угла сдвига и амплитуды
колебаний от времени для одного из
наблюдений.
9. Графики
Вывод:
Выполнив данную лабораторную работу,
мы провели исследование динамики
колебательного движения крутильного
маятника, и получили такие значения :
с ω0д=7±1 Гц
Tдк=1,344±0,017 с
ω0дк=4,7±0,9 Гц
k=0,449±0,013
1011 1/м3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F — частота (Гц), v — скорость распространения колебаний в среде (м/с), λ — длина волны (м).
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T — период колебаний (с), F — частота (Гц).
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F — частота (Гц), T — период колебаний (с).
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω — циклическая частота (радиан в секунду), F — обычная частота (Гц)
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω / (2π), где F — обычная частота (Гц), ω — циклическая частота (радиан в секунду).
Цель работы: вычислить ускорение свободного падения из формулы для периода колебаний математического маятника:
Для этого необходимо измерить период колебания и длину подвеса маятника. Тогда из формулы (1) можно вычислить ускорение свободного падения:
Средства измерения:
1) часы с секундной стрелкой;
2) измерительная лента (Δл = 0,5 см).
Материалы: 1) шарик с отверстием; 2) нить; 3) штатив с муфтой и кольцом.
Порядок выполнения работы
1. Установите на краю стола штатив. У его верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3—5 см от пола.
2. Отклоните маятник от положения равновесия на 5—8 см и отпустите его.
3. Измерьте длину подвеса мерной лентой.
4. Измерьте время Δt 40 полных колебаний (N).
5. Повторите измерения Δt (не изменяя условий опыта) и найдите среднее значение Δtср.
6. Вычислите среднее значение периода колебаний Tср по среднему значению Δtср.
7. Вычислите значение gcp по формуле:
8. Полученные результаты занесите в таблицу:
|
Номер опыта |
l, м |
N |
Δt, с |
Δtср, с |
 |
 |
9. Сравните полученное среднее значение для gcp со значением g = 9,8 м/с2 и рассчитайте относительную погрешность измерения по формуле:
Изучая курс физики вам часто приходилось использовать в решении задач и других расчетах значение ускорения свободного падения на поверхности земли. Вы принимали значение g = 9,81 м/с2, то есть с той точностью, которой вполне достаточно для производимых вами расчетов.
Целью данной лабораторной работы является экспериментальное установление ускорения свободного падения с помощью маятника. Зная формулу периода колебания математического маятника Т =
можно выразить значение g через величины, доступные простому установлению путем эксперимента и рассчитать g с некоторой точностью. Выразим
где l — длина подвеса, а Т — период колебаний маятника. Период колебаний маятника Т легко определить, измерив время t, необходимое для совершения некоторого количества N полных колебаний маятника
Математическим маятником называют груз, подвешенный к тонкой нерастяжимой нити, размеры которого много меньше длины нити, а масса — много больше массы нити. Отклонение этого груза от вертикали происходит на бесконечно малый угол, а трение отсутствует. В реальных условиях формула
имеет приблизительный характер.
Рассмотрим такое тело (в нашем случае рычаг). На него действуют две силы: вес грузов P и сила F (упругости пружины динамометра), чтобы рычаг находился в равновесии и моменты этих сил должны быть равны по модулю меду собой. Абсолютные значения моментов сил F и P определим соответственно:
В лабораторных условиях для измерения с некоторой степенью точности можно использовать небольшой, но массивный металлический шарик, подвешенный на нити длиной 1-1,5 м (или большей, если есть возможность такой подвес разместить) и отклонять его на небольшой угол. Ход работы целиком понятен из описания ее в учебнике.
Средства измерения: секундомер (Δt = ±0,5 с); линейка или измерительная лента (Δl = ±0,5 см)
Выполнение работы:
|
№ опыта |
1, м |
N |
t, с |
tср, с |
Тср |
gср, м/с2 |
|
1 |
1,5 |
40 |
100 |
|||
|
2 |
1,5 |
40 |
98 |
99 |
2,475 |
9,657 |
|
3 |
1,5 |
40 |
99 |
Вычисления:
Погрешность:
Как найти средний период колебаний?
На этой странице находится вопрос Как найти средний период колебаний?. Здесь же – ответы на него,
и похожие вопросы в категории Физика, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

 ,
, ,
,
 .
. ,
, ,
, ,
,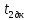 ,c
,c









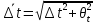



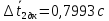





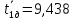








 .
.