In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, …, an, the geometric mean is defined as
or, equivalently, as the arithmetic mean in logscale:
Most commonly the numbers are restricted to being non-negative, to avoid complications related to negative numbers not having real roots, and frequently they are restricted to being positive, to enable the use of logarithms.
For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, 
![{displaystyle {sqrt[{3}]{4cdot 1cdot 1/32}}=1/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfd83c4a9ce55b2c53c47b9b32e0e99cf2b92bd8)
The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or interest rates of a financial investment over time. It also applies to benchmarking, where it is particularly useful for computing means of speedup ratios: since the mean of 0.5x (half as fast) and 2x (twice as fast) will be 1 (i.e., no speedup overall).
The geometric mean can be understood in terms of geometry. The geometric mean of two numbers, 






The geometric mean is one of the three classical Pythagorean means, together with the arithmetic mean and the harmonic mean. For all positive data sets containing at least one pair of unequal values, the harmonic mean is always the least of the three means, while the arithmetic mean is always the greatest of the three and the geometric mean is always in between (see Inequality of arithmetic and geometric means.)
Calculation[edit]
The geometric mean of a data set 
[3]
The above figure uses capital pi notation to show a series of multiplications. Each side of the equal sign shows that a set of values is multiplied in succession (the number of values is represented by «n») to give a total product of the set, and then the nth root of the total product is taken to give the geometric mean of the original set. For example, in a set of four numbers 



![{textstyle 24^{frac {1}{4}}={sqrt[{4}]{24}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebf902fd3a756ded31adb6422871b0f871873ab3)
Iterative means[edit]
The geometric mean of a data set is less than the data set’s arithmetic mean unless all members of the data set are equal, in which case the geometric and arithmetic means are equal. This allows the definition of the arithmetic-geometric mean, an intersection of the two which always lies in between.
The geometric mean is also the arithmetic-harmonic mean in the sense that if two sequences (

and
where 




Replacing the arithmetic and harmonic mean by a pair of generalized means of opposite, finite exponents yields the same result.
Relationship with logarithms[edit]
The geometric mean can also be expressed as the exponential of the arithmetic mean of logarithms.[4] By using logarithmic identities to transform the formula, the multiplications can be expressed as a sum and the power as a multiplication:
When 
- As:
- alternatively, use any positive real number base, for both the logarithms and the number you are raising to the power of the arithmetic mean of the individual logarithms at that same base.
additionally, if negative values of the 
where m is the number of negative numbers.
This is sometimes called the log-average (not to be confused with the logarithmic average). It is simply computing the arithmetic mean of the logarithm-transformed values of 



Related to the above, it can be seen that for a given sample of points 
,
whereas the arithmetic mean is the minimizer of
.
Thus, the geometric mean provides a summary of the samples whose exponent best matches the exponents of the samples (in the least squares sense).
The log form of the geometric mean is generally the preferred alternative for implementation in computer languages because calculating the product of many numbers can lead to an arithmetic overflow or arithmetic underflow. This is less likely to occur with the sum of the logarithms for each number.
Comparison to arithmetic mean[edit]
The geometric mean of a non-empty data set of (positive) numbers is always at most their arithmetic mean. Equality is only obtained when all numbers in the data set are equal; otherwise, the geometric mean is smaller. For example, the geometric mean of 2 and 3 is 2.45, while their arithmetic mean is 2.5. In particular, this means that when a set of non-identical numbers is subjected to a mean-preserving spread — that is, the elements of the set are «spread apart» more from each other while leaving the arithmetic mean unchanged — their geometric mean decreases.[5]
Average growth rate[edit]
In many cases the geometric mean is the best measure to determine the average growth rate of some quantity. (For example, if in one year sales increases by 80% and the next year by 25%, the end result is the same as that of a constant growth rate of 50%, since the geometric mean of 1.80 and 1.25 is 1.50.) In order to determine the average growth rate, it is not necessary to take the product of the measured growth rates at every step. Let the quantity be given as the sequence 




Application to normalized values[edit]
The fundamental property of the geometric mean, which does not hold for any other mean, is that for two sequences 

This makes the geometric mean the only correct mean when averaging normalized results; that is, results that are presented as ratios to reference values.[6] This is the case when presenting computer performance with respect to a reference computer, or when computing a single average index from several heterogeneous sources (for example, life expectancy, education years, and infant mortality). In this scenario, using the arithmetic or harmonic mean would change the ranking of the results depending on what is used as a reference. For example, take the following comparison of execution time of computer programs:
Table 1
| Computer A | Computer B | Computer C | |
|---|---|---|---|
| Program 1 | 1 | 10 | 20 |
| Program 2 | 1000 | 100 | 20 |
| Arithmetic mean | 500.5 | 55 | 20 |
| Geometric mean | 31.622 . . . | 31.622 . . . | 20 |
| Harmonic mean | 1.998 . . . | 18.182 . . . | 20 |
The arithmetic and geometric means «agree» that computer C is the fastest. However, by presenting appropriately normalized values and using the arithmetic mean, we can show either of the other two computers to be the fastest. Normalizing by A’s result gives A as the fastest computer according to the arithmetic mean:
Table 2
| Computer A | Computer B | Computer C | |
|---|---|---|---|
| Program 1 | 1 | 10 | 20 |
| Program 2 | 1 | 0.1 | 0.02 |
| Arithmetic mean | 1 | 5.05 | 10.01 |
| Geometric mean | 1 | 1 | 0.632 . . . |
| Harmonic mean | 1 | 0.198 . . . | 0.039 . . . |
while normalizing by B’s result gives B as the fastest computer according to the arithmetic mean but A as the fastest according to the harmonic mean:
Table 3
| Computer A | Computer B | Computer C | |
|---|---|---|---|
| Program 1 | 0.1 | 1 | 2 |
| Program 2 | 10 | 1 | 0.2 |
| Arithmetic mean | 5.05 | 1 | 1.1 |
| Geometric mean | 1 | 1 | 0.632 |
| Harmonic mean | 0.198 . . . | 1 | 0.363 . . . |
and normalizing by C’s result gives C as the fastest computer according to the arithmetic mean but A as the fastest according to the harmonic mean:
Table 4
| Computer A | Computer B | Computer C | |
|---|---|---|---|
| Program 1 | 0.05 | 0.5 | 1 |
| Program 2 | 50 | 5 | 1 |
| Arithmetic mean | 25.025 | 2.75 | 1 |
| Geometric mean | 1.581 . . . | 1.581 . . . | 1 |
| Harmonic mean | 0.099 . . . | 0.909 . . . | 1 |
In all cases, the ranking given by the geometric mean stays the same as the one obtained with unnormalized values.
However, this reasoning has been questioned.[7]
Giving consistent results is not always equal to giving the correct results. In general, it is more rigorous to assign weights to each of the programs, calculate the average weighted execution time (using the arithmetic mean), and then normalize that result to one of the computers. The three tables above just give a different weight to each of the programs, explaining the inconsistent results of the arithmetic and harmonic means (Table 4 gives equal weight to both programs, the Table 2 gives a weight of 1/1000 to the second program, and the Table 3 gives a weight of 1/100 to the second program and 1/10 to the first one). The use of the geometric mean for aggregating performance numbers should be avoided if possible, because multiplying execution times has no physical meaning, in contrast to adding times as in the arithmetic mean. Metrics that are inversely proportional to time (speedup, IPC) should be averaged using the harmonic mean.
The geometric mean can be derived from the generalized mean as its limit as 
Geometric mean of a continuous function[edit]
If ![{displaystyle f:[a,b]to (0,infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e9bf1b3d84aa538bedd5481abc3eadbba6cd12)
For instance, taking the identity function 

Applications[edit]
Proportional growth[edit]
The geometric mean is more appropriate than the arithmetic mean for describing proportional growth, both exponential growth (constant proportional growth) and varying growth; in business the geometric mean of growth rates is known as the compound annual growth rate (CAGR). The geometric mean of growth over periods yields the equivalent constant growth rate that would yield the same final amount.
Suppose an orange tree yields 100 oranges one year and then 180, 210 and 300 the following years, so the growth is 80%, 16.6666% and 42.8571% for each year respectively. Using the arithmetic mean calculates a (linear) average growth of 46.5079% (80% + 16.6666% + 42.8571%, that sum then divided by 3). However, if we start with 100 oranges and let it grow 46.5079% each year, the result is 314 oranges, not 300, so the linear average over-states the year-on-year growth.
Instead, we can use the geometric mean. Growing with 80% corresponds to multiplying with 1.80, so we take the geometric mean of 1.80, 1.166666 and 1.428571, i.e. ![{displaystyle {sqrt[{3}]{1.80times 1.166666times 1.428571}}approx 1.442249}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da9a200d95bde041252664366636b41eb7fb036)
Financial[edit]
The geometric mean has from time to time been used to calculate financial indices (the averaging is over the components of the index). For example, in the past the FT 30 index used a geometric mean.[8] It is also used in the recently introduced «RPIJ» measure of inflation in the United Kingdom and in the European Union.
This has the effect of understating movements in the index compared to using the arithmetic mean.[8]
[edit]
Although the geometric mean has been relatively rare in computing social statistics, starting from 2010 the United Nations Human Development Index did switch to this mode of calculation, on the grounds that it better reflected the non-substitutable nature of the statistics being compiled and compared:
- The geometric mean decreases the level of substitutability between dimensions [being compared] and at the same time ensures that a 1 percent decline in say life expectancy at birth has the same impact on the HDI as a 1 percent decline in education or income. Thus, as a basis for comparisons of achievements, this method is also more respectful of the intrinsic differences across the dimensions than a simple average.[9]
Not all values used to compute the HDI (Human Development Index) are normalized; some of them instead have the form 
The equally distributed welfare equivalent income associated with an Atkinson Index with an inequality aversion parameter of 1.0 is simply the geometric mean of incomes. For values other than one, the equivalent value is an Lp norm divided by the number of elements, with p equal to one minus the inequality aversion parameter.
Geometry[edit]
The altitude of a right triangle from its right angle to its hypotenuse is the geometric mean of the lengths of the segments the hypotenuse is split into. Using Pythagoras’ theorem on the 3 triangles of sides (p + q, r, s ), (r, p, h ) and (s, h, q ),
In the case of a right triangle, its altitude is the length of a line extending perpendicularly from the hypotenuse to its 90° vertex. Imagining that this line splits the hypotenuse into two segments, the geometric mean of these segment lengths is the length of the altitude. This property is known as the geometric mean theorem.
In an ellipse, the semi-minor axis is the geometric mean of the maximum and minimum distances of the ellipse from a focus; it is also the geometric mean of the semi-major axis and the semi-latus rectum. The semi-major axis of an ellipse is the geometric mean of the distance from the center to either focus and the distance from the center to either directrix.
Another way to think about it is as follows:
Consider a circle with radius 


Since the area of the circle and the ellipse stays the same, we have:

The radius of the circle is the geometric mean of the semi-major and the semi-minor axes of the ellipse formed by deforming the circle.
Distance to the horizon of a sphere (ignoring the effect of atmospheric refraction when atmosphere is present) is equal to the geometric mean of the distance to the closest point of the sphere and the distance to the farthest point of the sphere.
The geometric mean is used in both in the approximation of squaring the circle by S.A. Ramanujan[10] and in the construction of the heptadecagon with «mean proportionals».[11]
Aspect ratios[edit]
Equal area comparison of the aspect ratios used by Kerns Powers to derive the SMPTE 16:9 standard.[12] TV 4:3/1.33 in red,
1.66 in orange,
16:9/1.77 in blue,
1.85 in yellow,
Panavision/2.2 in mauve and
CinemaScope/2.35 in purple.
The geometric mean has been used in choosing a compromise aspect ratio in film and video: given two aspect ratios, the geometric mean of them provides a compromise between them, distorting or cropping both in some sense equally. Concretely, two equal area rectangles (with the same center and parallel sides) of different aspect ratios intersect in a rectangle whose aspect ratio is the geometric mean, and their hull (smallest rectangle which contains both of them) likewise has the aspect ratio of their geometric mean.
In the choice of 16:9 aspect ratio by the SMPTE, balancing 2.35 and 4:3, the geometric mean is 



Applying the same geometric mean technique to 16:9 and 4:3 approximately yields the 14:9 (



Paper formats[edit]
The geometric mean is also used to calculate B and C series paper formats. The 






The same principle applies with the C series, whose area is the geometric mean of the A and B series. For example, the C4 format has an area which is the geometric mean of the areas of A4 and B4.
An advantage that comes from this relationship is that an A4 paper fits inside a C4 envelope, and both fit inside a B4 envelope.
Other applications[edit]
- Spectral flatness: in signal processing, spectral flatness, a measure of how flat or spiky a spectrum is, is defined as the ratio of the geometric mean of the power spectrum to its arithmetic mean.
- Anti-reflective coatings: In optical coatings, where reflection needs to be minimised between two media of refractive indices n0 and n2, the optimum refractive index n1 of the anti-reflective coating is given by the geometric mean:
.
- Subtractive color mixing: The spectral reflectance curve for paint mixtures (of equal tinting strength, opacity and dilution) is approximately the geometric mean of the paints’ individual reflectance curves computed at each wavelength of their spectra.[14]
- Image processing: The geometric mean filter is used as a noise filter in image processing.
- Labor compensation: The geometric mean of a subsistence wage and market value of the labor using capital of employer was suggested as the natural wage by Johann von Thünen in 1875.[15]
See also[edit]
- Arithmetic-geometric mean
- Generalized mean
- Geometric mean theorem
- Geometric standard deviation
- Harmonic mean
- Heronian mean
- Heteroscedasticity
- Log-normal distribution
- Muirhead’s inequality
- Product
- Pythagorean means
- Quadratic mean
- Quadrature (mathematics)
- Quasi-arithmetic mean (generalized f-mean)
- Rate of return
- Weighted geometric mean
Notes[edit]
- ^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.
References[edit]
- ^ Matt Friehauf, Mikaela Hertel, Juan Liu, and Stacey Luong «On Compass and Straightedge Constructions: Means» (PDF). UNIVERSITY of WASHINGTON, DEPARTMENT OF MATHEMATICS. 2013. Retrieved 14 June 2018.
- ^ «Euclid, Book VI, Proposition 13». David E. Joyce, Clark University. 2013. Retrieved 19 July 2019.
- ^ «2.5: Geometric Mean». Statistics LibreTexts. 2019-04-20. Retrieved 2021-08-16.
- ^ Crawley, Michael J. (2005). Statistics: An Introduction using R. John Wiley & Sons Ltd. ISBN 9780470022986.
- ^ Mitchell, Douglas W. (2004). «More on spreads and non-arithmetic means». The Mathematical Gazette. 88: 142–144. doi:10.1017/S0025557200174534. S2CID 168239991.
- ^ Fleming, Philip J.; Wallace, John J. (1986). «How not to lie with statistics: the correct way to summarize benchmark results». Communications of the ACM. 29 (3): 218–221. doi:10.1145/5666.5673. S2CID 1047380.
- ^ Smith, James E. (1988). «Characterizing computer performance with a single number». Communications of the ACM. 31 (10): 1202–1206. doi:10.1145/63039.63043. S2CID 10805363.
- ^ a b Rowley, Eric E. (1987). The Financial System Today. Manchester University Press. ISBN 0719014875.
- ^ «Frequently Asked Questions — Human Development Reports». hdr.undp.org. Archived from the original on 2011-03-02.
- ^ Ramanujan, S. (1914). «Modular equations and approximations to π» (PDF). Quarterly Journal of Mathematics. 45: 350–372.
- ^ T.P. Stowell Extract from Leybourn’s Math. Repository, 1818 in The Analyst via Google Books
- ^ a b «TECHNICAL BULLETIN: Understanding Aspect Ratios» (PDF). The CinemaSource Press. 2001. Archived (PDF) from the original on 2009-09-09. Retrieved 2009-10-24.
- ^ US 5956091, «Method of showing 16:9 pictures on 4:3 displays», issued September 21, 1999
- ^ MacEvoy, Bruce. «Colormaking Attributes: Measuring Light & Color». handprint.com/LS/CVS/color.html. Colorimetry. Archived from the original on 2019-07-14. Retrieved 2020-01-02.
- ^ Henry Ludwell Moore (1895). Von Thünen’s Theory of Natural Wages. G. H. Ellis.
External links[edit]
- Calculation of the geometric mean of two numbers in comparison to the arithmetic solution
- Arithmetic and geometric means
- When to use the geometric mean
- Practical solutions for calculating geometric mean with different kinds of data Archived 2010-11-12 at the Wayback Machine
- Geometric Mean on MathWorld
- Geometric Meaning of the Geometric Mean
- Geometric Mean Calculator for larger data sets
- Computing Congressional apportionment using Geometric Mean
- Non-Newtonian calculus website
- Geometric Mean Definition and Formula
- The Distribution of the Geometric Mean
- The geometric mean?
Загрузить PDF
Загрузить PDF
Среднее геометрическое — математическая величина, которую легко спутать с более часто применяемым средним арифметическим. Для вычисления среднего геометрического следуйте методам, приведенным ниже.
-
1
Возьмите два числа, среднее геометрическое которых необходимо найти.
- Например, 2 и 32.
-
2
-
3
Реклама
-
1
Подставьте числа в приведенное уравнение. Если это, скажем, 10 и 15, то подставьте их так, как показано на рисунке.
-
2
Найдите «х». Начните с перемножения крест-накрест, что означает перемножение пар чисел по диагонали и расстановку результатов умножения по разные стороны знака =. Так как х*х = х2, то уравнение приводится к виду к виду: х2 = (результат умножения ваших чисел). Для вычисления «х» извлеките квадратный корень из результата перемножения используемых чисел. Если в результате вычисления корня получится целое число — отлично. Если нет, дайте ответ в виде десятичной дроби или запишите его со знаком корня (в зависимости от того, что требует преподаватель). Ответ, приведенный выше на рисунке, записан в виде упрощенного квадратного корня.
Реклама
-
1
Подставьте числа в приведенное уравнение.Среднее геометрическое = (a1 × a2 . . . an)1/n[3]
- a1 — первое число, a2 — второе число и так далее
- n — общее количество чисел
-
2
Перемножьте числа (a1, a2 и так далее).
-
3
Извлеките корень n степени из полученного числа. Это и будет среднее геометрическое.[4]
Реклама
-
1
Найдите логарифм каждого числа и сложите полученные значения. Найдите клавишу LOG на своем калькуляторе. Затем введите: (первое число) LOG + (второе число) LOG + (третье число) LOG [+ столько чисел, сколько дано] =. Не забудьте нажать «=», или показанный вам результат будет логарифмом последнего введенного числа, а не суммой логарифмов всех чисел.
- Например, log 7 + log 9 + log 12 = 2,878521796
-
2
Разделите результат сложения на общее количество изначально данных чисел. Если вы сложили логарифмы трех чисел, делите полученный результат на три.
- Например, 2,878521796 / 3 = 0,959507265
-
3
Вычислите антилогарифм полученного результата. На калькуляторе нажмите кнопку переключения регистра (активирует функции верхнего регистра — над клавишами), а затем нажмите LOG, чтобы получить значение антилогарифма. Этот результат и будет средним геометрическим.[5]
- Например, antilog 0,959507265 = 9,109766916. Поэтому среднее геометрическое 7, 9, и 12 равно 9,11.
Реклама
Советы
- Различия между средним арифметическим и средним геометрическим:
- Для вычисления среднего арифметического, например, чисел 3, 4 и 18, необходимо их сложить 3 + 4 + 18, а затем разделить на 3 (потому что изначально даны три числа). Ответ равен 25/3 или примерно 8,333; это означает, что если сложить 8,3333 три раза подряд, то ответ будет таким же, как при сложении чисел 3, 4, и 18. Среднее арифметическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при суммировании получился один результат?»
- Напротив, среднее геометрическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при перемножении получился один результат?» Поэтому, чтобы найти среднее геометрическое чисел 3, 4 и 18, мы перемножаем эти числа: 3 x 4 x 18. Получаем 216. Затем мы берем кубический корень из полученного результата перемножения (кубический корень, так как в вычислении участвуют три числа). Ответ будет 6. Другими словами, так как 6 x 6 x 6 = 3 x 4 x 18, то 6 является средним геометрическим чисел 3, 4 и 18.
- Среднее геометрическое всегда меньше или равно среднему арифметическому. Более подробно читайте тут.
- Среднее геометрическое рассчитывается только для положительных чисел. Схема решения различных прикладных задач с использованием среднего геометрического не будет работать в случае наличия отрицательных чисел.
Реклама
Об этой статье
Эту страницу просматривали 131 835 раз.
Была ли эта статья полезной?
Пропорциональные отрезки в прямоугольном треугольнике
В этом уроке познакомимся с понятием «среднее геометрическое» или «среднее пропорциональное» для отрезков, выведем формулы для вычисления высоты и катетов прямоугольного треугольника через понятие среднее пропорциональное, рассмотрим задачу на применение формул.
Решим задачу:
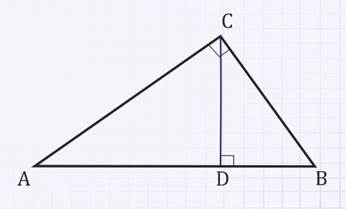
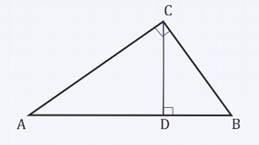
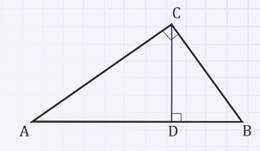
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:
∆АВС – прямоугольный треугольник,
СD – высота, проведенная из вершины С к гипотенузе АВ.
Доказать:
∆АВС ~ ∆АСD;
∆АВС ~ ∆CBD
∆АСD ~ ∆CBD.
Доказательство:
1)Рассмотрим треугольники АВС и АСD.
Так как ∠А–общий,
∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.
2)Рассмотрим треугольники АВС и СВD.
Так как ∠В–общий,
∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.
3)Рассмотрим треугольники АСD и СВD.
Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.
Что и требовалось доказать.
В геометрии в формулировках ряда утверждений и при решении отдельных задач используется понятие «среднее пропорциональное отрезков» или «среднее геометрическое».
Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:
Исходя из доказанной выше задачи, можно выделить два утверждения.
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Для вывода данного утверждения воспользуемся доказанным, а именно, что:
поэтому:
Применяя основное свойство пропорции, получим
2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Также по выше доказанному в задаче:
поэтому:
и, следовательно:
Решим задачу, применяя данные утверждения.
Задача:
Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.
Решение:
Найдем гипотенузу данного прямоугольного треугольника:
Теперь воспользуемся равенством второго утверждения:
Для вычисления второго катета воспользуемся теоремой Пифагора:
или равенством все того же второго утверждения:
Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.
Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей). В общем случае среднее геометрическое рассчитывается по формуле:
То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения
Среднее геометрическое трех чисел – кубический корень из произведения
и т.д.
Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.
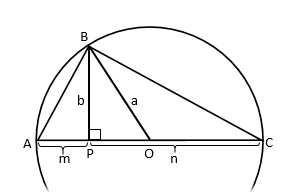
Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.
Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.
Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство
Откуда
Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.
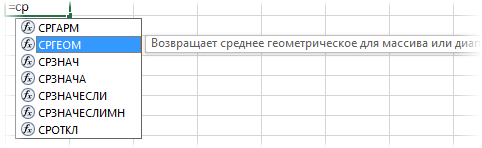
В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.
Все очень просто: вызвали функцию, указали диапазон и готово.
На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.
Ниже видео, как найти среднее геометрическое чисел в Excel.
Поделиться в социальных сетях:
В математике среднее геометрическое — это среднее или среднее значение , которое указывает на центральную тенденцию или типичное значение набора чисел с помощью произведения их значений (в отличие от среднего арифметического, которое использует их сумму). Среднее геометрическое определяется как п — й корень из произведения из п чисел, то есть, для набора чисел х 1 , х 2 , …, х п , среднее геометрическое определяется как
Например, среднее геометрическое двух чисел, скажем 2 и 8, является просто квадратным корнем из их произведения, то есть . В качестве другого примера, среднее геометрическое трех чисел 4, 1 и 1/32 является кубическим корнем из их произведения (1/8), равного 1/2, то есть . Среднее геометрическое применяется только к положительным числам.
Среднее геометрическое часто используется для набора чисел, значения которых предназначены для перемножения или являются экспоненциальными по своей природе, например набор цифр роста: значения человеческого населения или процентные ставки финансовых вложений с течением времени.
Среднее геометрическое можно понять с точки зрения геометрии . Среднее геометрическое двух чисел, и , — это длина одной стороны квадрата , площадь которого равна площади прямоугольника со сторонами длиной и . Точно так же, геометрическое среднее из трех чисел, , , и , длина одного края куба , объем которого такой же , как у параллелепипеда со сторонами, длина которых равна трем заданных чисел.
Среднее геометрическое — одно из трех классических средних пифагорова , вместе со средним арифметическим и гармоническим средним . Для всех положительных наборов данных, содержащих хотя бы одну пару неравных значений, гармоническое среднее всегда является наименьшим из трех средних, в то время как среднее арифметическое всегда является наибольшим из трех, а среднее геометрическое всегда находится посередине (см. Неравенство арифметики и геометрические средства .)
Расчет
Среднее геометрическое значение набора данных определяется как:
На приведенном выше рисунке используется запись с большой буквы, чтобы показать серию умножений. Каждая сторона знака равенства показывает, что набор значений последовательно умножается (количество значений представлено буквой «n»), чтобы получить общий продукт набора, а затем корень n- й степени из общего произведения берется в укажите среднее геометрическое для исходного набора. Например, в наборе из четырех чисел произведение равно , а среднее геометрическое — это корень четвертой степени из 24, или ~ 2,213. Показатель в левой части эквивалентен извлечению корня n- й степени. Например, .
Итерационные средства
Среднее геометрическое значение набора данных меньше среднего арифметического набора данных, если только все элементы набора данных не равны, и в этом случае геометрическое и среднеарифметическое значение равны. Это позволяет определить среднее арифметико-геометрическое , пересечение двух, которое всегда находится между ними.
Среднее геометрическое также является средним арифметически-гармоническим в том смысле, что если определены две последовательности ( ) и ( ):
а также
где — гармоническое среднее предыдущих значений двух последовательностей, тогда и будет сходиться к среднему геометрическому для и .
В этом легко убедиться из того факта, что последовательности сходятся к общему пределу (что можно показать с помощью теоремы Больцано – Вейерштрасса ) и того факта, что среднее геометрическое сохраняется:
Замена арифметического и гармонического среднего парой обобщенных средних противоположных конечных показателей дает тот же результат.
Связь с логарифмами
Среднее геометрическое также может быть выражено как экспонента среднего арифметического логарифмов. Используя логарифмические тождества для преобразования формулы, умножения можно выразить как сумму, а степень как умножение:
Когда 
дополнительно, если разрешены отрицательные значения ,
где m — количество отрицательных чисел.
Иногда это называется логарифмическим средним (не путать с логарифмическим средним ). Это просто вычисление среднего арифметического значений, преобразованных в логарифм (т. Е. Среднего арифметического в логарифмической шкале), а затем использование возведения в степень, чтобы вернуть вычисление к исходному масштабу, т. Е. Это обобщенное f-среднее с . Например, среднее геометрическое 2 и 8 можно рассчитать следующим образом, где — любое основание логарифма (обычно 2 или 10):
В связи с вышеизложенным можно видеть, что для данной выборки точек среднее геометрическое является минимизатором
-
,
тогда как среднее арифметическое является минимизатором
-
.
Таким образом, среднее геометрическое представляет собой сводку выборок, показатель степени которых лучше всего соответствует показателям степени образцов (в смысле наименьших квадратов).
Логарифмическая форма среднего геометрического обычно является предпочтительной альтернативой для реализации на компьютерных языках, потому что вычисление произведения многих чисел может привести к арифметическому переполнению или потере значимости . Это менее вероятно с суммой логарифмов для каждого числа.
Сравнение со средним арифметическим
Среднее геометрическое для непустого набора данных (положительных) чисел всегда равно их среднему арифметическому. Равенство достигается только тогда, когда все числа в наборе данных равны; в противном случае среднее геометрическое меньше. Например, среднее геометрическое 242 и 288 равно 264, а их среднее арифметическое — 265. В частности, это означает, что когда набор неидентичных чисел подвергается сохраняющему среднее значение разбросу, то есть элементам множества «разнесены» больше друг от друга, при этом среднее арифметическое остается неизменным — их среднее геометрическое уменьшается.
Средняя скорость роста
Во многих случаях среднее геометрическое является лучшим показателем для определения средней скорости роста некоторой величины. (Например, если в течение одного года продажи увеличиваются на 80%, а в следующем году на 25%, конечный результат будет таким же, как и при постоянном темпе роста в 50%, поскольку среднее геометрическое 1,80 и 1,25 равно 1,50.) Для определения средней скорости роста необязательно брать произведение измеренных темпов роста на каждом этапе. Пусть количество задается в виде последовательности , где — количество шагов от начального до конечного состояния. Скорость роста между последовательными измерениями и составляет . Среднее геометрическое этих темпов роста тогда просто:
Применение к нормированным значениям
Фундаментальное свойство среднего геометрического, который не имеет места для любого другого среднего значения, является то , что в течение двух последовательностей и одинаковой длины,
Это делает среднее геометрическое единственно правильным средним при усреднении нормализованных результатов; то есть результаты, которые представлены как отношения к контрольным значениям. Это имеет место при представлении производительности компьютера по сравнению с эталонным компьютером или при вычислении единого среднего индекса из нескольких разнородных источников (например, ожидаемая продолжительность жизни, годы образования и младенческая смертность). В этом сценарии использование среднего арифметического или гармонического приведет к изменению ранжирования результатов в зависимости от того, что используется в качестве эталона. Например, возьмем следующее сравнение времени выполнения компьютерных программ:
| Компьютер А | Компьютер B | Компьютер C | |
|---|---|---|---|
| Программа 1 | 1 | 10 | 20 |
| Программа 2 | 1000 | 100 | 20 |
| Среднее арифметическое | 500,5 | 55 | 20 |
| Среднее геометрическое | 31,622. . . | 31,622. . . | 20 |
| Гармоническое среднее | 1.998. . . | 18.182. . . | 20 |
Средние арифметические и геометрические «согласны», что компьютер C самый быстрый. Однако, представляя соответствующим образом нормализованные значения и используя среднее арифметическое, мы можем показать, что любой из двух других компьютеров является самым быстрым. Нормализация по результату A дает A как самый быстрый компьютер согласно среднему арифметическому:
| Компьютер А | Компьютер B | Компьютер C | |
|---|---|---|---|
| Программа 1 | 1 | 10 | 20 |
| Программа 2 | 1 | 0,1 | 0,02 |
| Среднее арифметическое | 1 | 5,05 | 10.01 |
| Среднее геометрическое | 1 | 1 | 0,632. . . |
| Гармоническое среднее | 1 | 0,198. . . | 0,039. . . |
в то время как нормализация по результату B дает B как самый быстрый компьютер согласно среднему арифметическому, но A как самый быстрый согласно среднему гармоническому:
| Компьютер А | Компьютер B | Компьютер C | |
|---|---|---|---|
| Программа 1 | 0,1 | 1 | 2 |
| Программа 2 | 10 | 1 | 0,2 |
| Среднее арифметическое | 5,05 | 1 | 1.1 |
| Среднее геометрическое | 1 | 1 | 0,632 |
| Гармоническое среднее | 0,198. . . | 1 | 0,363. . . |
и нормализация на результат C дает C как самый быстрый компьютер согласно среднему арифметическому, но A как самый быстрый согласно среднему гармоническому:
| Компьютер А | Компьютер B | Компьютер C | |
|---|---|---|---|
| Программа 1 | 0,05 | 0,5 | 1 |
| Программа 2 | 50 | 5 | 1 |
| Среднее арифметическое | 25,025 | 2,75 | 1 |
| Среднее геометрическое | 1.581. . . | 1.581. . . | 1 |
| Гармоническое среднее | 0,099. . . | 0,909. . . | 1 |
Во всех случаях рейтинг, определяемый средним геометрическим, остается таким же, как и рейтинг, полученный с ненормализованными значениями.
Однако это рассуждение было поставлено под сомнение. Давать стабильные результаты не всегда равносильно получению правильных результатов. Как правило, более строго назначать веса каждой из программ, вычислять средневзвешенное время выполнения (используя среднее арифметическое), а затем нормализовать этот результат на одном из компьютеров. В трех приведенных выше таблицах просто присваивается разный вес каждой из программ, объясняя несовместимые результаты средних арифметических и гармонических (первая таблица дает одинаковый вес обеим программам, вторая дает вес 1/1000 второй программе, а третий дает вес 1/100 второй программе и 1/10 первой). По возможности следует избегать использования среднего геометрического для агрегирования показателей производительности, потому что умножение времени выполнения не имеет физического смысла, в отличие от сложения времени, как в среднем арифметическом. Показатели, обратно пропорциональные времени (ускорение, IPC ), следует усреднять с использованием гармонического среднего.
Среднее геометрическое может быть получено из обобщенного среднего, поскольку его предел стремится к нулю. Точно так же это возможно для средневзвешенного геометрического.
Среднее геометрическое непрерывной функции
Если — непрерывная вещественнозначная функция, ее среднее геометрическое на этом интервале равно
Например, взятие тождественной функции на единичном интервале показывает, что среднее геометрическое положительных чисел от 0 до 1 равно .
Приложения
Пропорциональный рост
Среднее геометрическое более подходит, чем среднее арифметическое, для описания пропорционального роста, как экспоненциального роста (постоянный пропорциональный рост), так и переменного роста; в бизнесе среднее геометрическое значение темпов роста известно как совокупный годовой темп роста (CAGR). Среднее геометрическое значение роста за периоды дает эквивалентную постоянную скорость роста, которая дает такую же конечную сумму.
Предположим, апельсиновое дерево дает 100 апельсинов в год, а затем 180, 210 и 300 в последующие годы, поэтому рост составит 80%, 16,6666% и 42,8571% за каждый год соответственно. Используя среднее арифметическое, вычисляется (линейный) средний рост 46,5079% (80% + 16,6666% + 42,8571%, эта сумма затем делится на 3). Однако, если мы начнем со 100 апельсинов и позволим им расти на 46,5079% каждый год, в результате получится 314 апельсинов, а не 300, поэтому линейное среднее значение превышает годовой рост.
Вместо этого мы можем использовать среднее геометрическое. Рост с 80% соответствует умножению с 1.80, поэтому мы возьмем среднее геометрическое 1,80, 1.166666 и 1.428571, то есть ; таким образом, «средний» рост в год составляет 44,2249%. Если мы начнем со 100 апельсинов и позволим их количеству расти на 44,2249% каждый год, в результате получится 300 апельсинов.
Финансовый
Среднее геометрическое время от времени использовалось для расчета финансовых показателей (усреднение проводится по компонентам индекса). Например, в прошлом индекс FT 30 использовал среднее геометрическое. Он также используется в недавно введенном показателе инфляции RPIJ в Соединенном Королевстве и в Европейском Союзе.
Это приводит к занижению динамики индекса по сравнению с использованием среднего арифметического.
Хотя среднее геометрическое используется относительно редко при вычислении социальной статистики, начиная с 2010 года Индекс человеческого развития Организации Объединенных Наций действительно перешел на этот способ расчета на том основании, что он лучше отражает незаменимый характер собираемых и сравниваемых статистических данных:
- Среднее геометрическое снижает уровень взаимозаменяемости между [сравниваемыми] измерениями и в то же время гарантирует, что снижение предполагаемой продолжительности жизни при рождении на 1 процент оказывает такое же влияние на ИЧР, как снижение уровня образования или дохода на 1 процент. Таким образом, в качестве основы для сравнения достижений этот метод также более уважительно относится к внутренним различиям по измерениям, чем к простому среднему.
Не все значения, используемые для расчета ИЧР (индекса человеческого развития) , нормализованы; некоторые из них вместо этого имеют форму . Это делает выбор среднего геометрического менее очевидным, чем можно было бы ожидать в разделе «Свойства» выше.
Равномерно распределенный доход, эквивалентный благосостоянию, связанный с индексом Аткинсона с параметром неприятия неравенства, равным 1,0, является просто геометрическим средним доходом. Для значений, отличных от единицы, эквивалентное значение представляет собой норму Lp, деленную на количество элементов, где p равно единице минус параметр неприятия неравенства.
Геометрия
Высота прямоугольного треугольника от его прямого угла до гипотенузы — это среднее геометрическое длин отрезков, на которые разбита гипотенуза. Используя теорему Пифагора о трех треугольниках со сторонами ( p + q , r , s ) , ( r , p , h ) и ( s , h , q ) ,

В случае прямоугольного треугольника его высота равна длине линии, идущей перпендикулярно от гипотенузы до ее вершины 90 °. Если представить, что эта линия разделяет гипотенузу на два сегмента, среднее геометрическое значение длины этих сегментов равно длине высоты. Это свойство известно как теорема о среднем геометрическом .
В эллипсу , то ось полу-минор представляет собой среднее геометрическое максимальных и минимальных расстояний эллипса от фокуса ; это также среднее геометрическое значение большой полуоси и прямой полуоси . Большая полуось эллипса является средней геометрическим расстоянием от центра до любой направленности и расстояния от центра до любой директрисы .
Расстояние до горизонта в виде шара приблизительно равна среднему геометрическому расстоянию до ближайшей точки сферы , а расстояние до самой дальней точки сферы , когда расстояние до ближайшей точки сферы мало.
Как при приближении квадрата круга согласно С.А. Рамануджану (1914), так и при построении гептадекагона согласно «посланному Т.П. Стоуэллом, зачисленному в Leybourn’s Math. Repository, 1818» , используется среднее геометрическое.
Соотношения сторон
Сравнение равных площадей соотношений сторон, использованных Кернсом Пауэрсом для вывода стандарта SMPTE 16: 9 .
TV 4: 3 / 1,33 в красном, 1,66 в оранжевом, 16: 9 / 1,7 7 синим цветом , 1,85 в желтом, Panavision /2.2 в сиреневом и CinemaScope / 2.35 фиолетового цвета.
Среднее геометрическое использовалось при выборе компромиссного соотношения сторон в фильмах и видео: учитывая два соотношения сторон, их среднее геометрическое обеспечивает компромисс между ними, искажая или обрезая оба в некотором смысле одинаково. Конкретно, два прямоугольника равной площади (с одинаковым центром и параллельными сторонами) с разными соотношениями сторон пересекаются в прямоугольнике, соотношение сторон которого является средним геометрическим, а их корпус (наименьший прямоугольник, который содержит оба из них) также имеет соотношение сторон их среднее геометрическое.
При выборе формата изображения 16: 9 с помощью SMPTE , балансировки 2,35 и 4: 3, было выбрано среднее геометрическое , и поэтому … Это было эмпирически обнаружено Кернсом Пауэрсом, который вырезал прямоугольники с равными площадями и придал им форму, соответствующую каждому из популярных соотношений сторон. При наложении их центральных точек, выровненных, он обнаружил, что все эти прямоугольники с соотношением сторон помещаются во внешний прямоугольник с соотношением сторон 1,77: 1, и все они также покрывают меньший общий внутренний прямоугольник с тем же соотношением сторон 1,77: 1. Значение, найденное Пауэрсом, является в точности средним геометрическим для крайних соотношений сторон, 4: 3 (1,33: 1) и CinemaScope (2,35: 1), что по совпадению близко к ( ). Промежуточные соотношения не влияют на результат, только два крайних соотношения.

Применение того же метода среднего геометрического к 16: 9 и 4: 3 приблизительно дает соотношение сторон 14: 9 ( …), которое также используется в качестве компромисса между этими соотношениями. В этом случае 14: 9 — это в точности среднее арифметическое числа и , поскольку 14 — это среднее значение 16 и 12, в то время как точное геометрическое среднее — это всего лишь два разных средства , арифметическое и геометрическое, приблизительно равны, поскольку оба числа достаточно близки к друг друга (разница менее 2%).
Спектральная плоскостность
В обработке сигналов , спектральная плоскостности , мера того , насколько плоским или остроконечный спектр есть, определяются как отношение среднего геометрического спектра мощности к его среднему арифметическому.
Антибликовые покрытия
В оптических покрытиях, где отражение должны быть сведено к минимуму между двумя средами преломления п 0 и п 2 , оптимальным показателем преломлением п 1 из антибликового покрытия даются геометрическим средним: .
Субтрактивное смешение цветов
Спектральный коэффициент отражения кривой для краски смесей (равного колеровочной прочности, непрозрачности и разбавления ) составляет примерно среднее геометрическое отдельных кривых отражения красок , вычисленных на каждой длине волны их спектров .
Обработка изображений
Средний геометрический фильтр используется в качестве фильтра шума в обработке изображений .
Смотрите также
- Среднее арифметико-геометрическое
- Обобщенное среднее
- Геометрическая теорема о среднем
- Стандартное геометрическое отклонение
- Гармоническое среднее
- Среднее геронское
- Гетероскедастичность
- Гиперболические координаты
- Логнормальное распределение
- Неравенство Мюрхеда
- Продукт
- Пифагорейские средства
- Квадратичное среднее
- Квадратура (математика)
- Квазиарифметическое среднее ( обобщенное f-среднее )
- Норма прибыли
- Среднее геометрическое взвешенное
Примечания и ссылки
внешние ссылки
- Вычисление среднего геометрического двух чисел по сравнению с арифметическим решением
- Средние арифметические и геометрические
- Когда использовать среднее геометрическое
- Практические решения для расчета среднего геометрического с различными типами данных
- Среднее геометрическое в MathWorld
- Геометрическое значение среднего геометрического
- Калькулятор среднего геометрического для больших наборов данных
- Расчет пропорционального распределения Конгресса с использованием среднего геометрического
- Сайт неньютоновского исчисления
- Определение среднего геометрического и формула


![{displaystyle left(prod _{i=1}^{n}a_{i}right)^{frac {1}{n}}={sqrt[{n}]{a_{1}a_{2}cdots a_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b67da21f4b58d3121ef21e0c5a9d040a6b65ce)

![{displaystyle left(prod _{i=1}^{n}a_{i}right)^{frac {1}{n}}={sqrt[{n}]{a_{1}a_{2}cdots a_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02ce0b254fa59ff1469815211849e01afb2c2639)



![{displaystyle left(prod _{i=1}^{n}a_{i}right)^{frac {1}{n}}=exp left[{frac {1}{n}}sum _{i=1}^{n}ln a_{i}right];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bebc299146b954703f19c2b6d77dec555813fac7)
![{displaystyle {begin{aligned}left(prod _{i=1}^{n}a_{i}right)^{frac {1}{n}}&={sqrt[{n}]{a_{1}a_{2}cdots a_{n}}}\&=e^{ln(a_{1}a_{2}cdots a_{n})^{1/n}}\&=e^{{frac {1}{n}}left(ln a_{1}+ln a_{2}+cdots +ln a_{n}right)}\&=e^{{frac {1}{n}}sum _{i=1}^{n}ln a_{i}}\{text{geometric mean(}}a{text{)}}&=e^{{text{arithmetic mean(ln(}}a{text{))}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c20284ee16e7627c22ce1c8388d96a3c08771f)
![{displaystyle left(prod _{i=1}^{n}a_{i}right)^{frac {1}{n}}=left(left(-1right)^{m}right)^{frac {1}{n}}exp left[{frac {1}{n}}sum _{i=1}^{n}ln left|a_{i}right|right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/598e2e9ba9f34556b6e603997e98453114daa329)
![{displaystyle b^{{frac {1}{2}}left[log _{b}(2)+log _{b}(8)right]}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464b46540b9c48ef7d26669a6b08b330425a017f)






![{displaystyle {text{GM}}[f]=exp left({frac {1}{b-a}}int _{a}^{b}ln f(x)dxright)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd70a2776c189e5361b786a6e5121c57addfe52b)














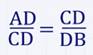
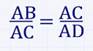
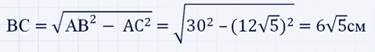
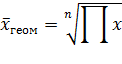
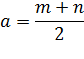
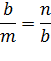
![{ displaystyle left ( prod _ {i = 1} ^ {n} x_ {i} right) ^ { frac {1} {n}} = { sqrt [{n}] {x_ {1} x_ {2} cdots x_ {n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026cae6801f672b9858d55935ec7397183dc3a36)

