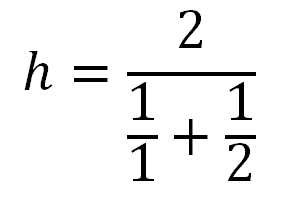Среднее гармоническое
Среднее гармоническое — один из способов определения среднего значения числового ряда (наряду с медианой и средним арифметическим). Мы сделали калькулятор, который может рассчитать среднее гармоническое двух, трех — да любого количества чисел.
Рассчитывается среднее гармоническое по простой формуле и является обратной величиной к среднему от обратных к числам.
Среднее гармоническое удобно применять для решения задач, которые начинаются словами «первую половину пути автомобиль проехал со скоростью…». Например, первую половину пути автомобиль проехал со скоростью 60 км/ч вторую 90 км/ч. Найдите среднюю скорость. Просто введите в калькулятор два числа — 60 и 90 и получите ответ — 72 км/ч.
Калькулятор среднего гармонического
Как найти среднее гармоническое чисел
Лучше показать это на примере. Найдем среднее гармоническое двух чисел 1 и 2. Подставив значения в формулу получим такое выражение:
Здесь в числителе количество чисел (2), а в знаменателе сами числа. В результате расчета получаем, что среднее геометрическое чисел 1 и 2 равно 1,6666… или 1,(6).
Ваша оценка
[Оценок: 163 Средняя: 3.2]
Среднее гармоническое Автор admin средний рейтинг 3.2/5 — 163 рейтинги пользователей
Download Article
Download Article
The harmonic mean is a way to calculate the mean, or average, of a set of numbers. Using the harmonic mean is most appropriate when the set of numbers contains outliers that might skew the result. Most people are familiar with calculating the arithmetic mean, in which the sum of values is divided by the number of values. Calculating the harmonic mean is a little more complicated. If working with a small set of numbers you may be able to solve by hand using the formula. Otherwise, you can easily use Microsoft Excel to find the harmonic mean.
-
1
Set up the formula for the harmonic mean. The formula is
, where is the number of values in the set of numbers, and , , are the values in the set.[1]
-
2
Determine the values you need to find the harmonic mean for. This can be any set of numbers.[2]
- For example, you may need to find the harmonic mean for the numbers 10, 12, 16, and 8.
Advertisement
-
3
Plug the value of
into the formula. This will equal the number of values in your set.
- For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4:
- For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4:
-
4
Plug the values your are averaging into your formula. You will take the reciprocal of each number and add them in the denominator of the formula. Remember, when you take the reciprocal of a whole number, you turn the number into a fraction by placing a 1 in the numerator and the whole number in the denominator.[3]
Advertisement
-
1
Add the fractions in the denominator. You can use a calculator, or add them up by hand. If you are not using a calculator, remember to find a common denominator first. To learn more about adding fractions, read Add Fractions.
- For example:
- For example:
-
2
Divide the numerator by the denominator. Remember that dividing by a fraction is the same as multiplying by its reciprocal.[4]
-
3
Convert to a decimal to find the harmonic mean of your set of numbers. To convert a fraction to a decimal, divide the numerator by the denominator.[5]
Advertisement
-
1
Enter the values into your spreadsheet. Make sure to only place one value in each cell.
- For example, if you need to find the harmonic mean of 10, 12, 16, and 8, you might type each of these values into a separate cell in the spreadsheet, cells A1-A4.
-
2
Enter the function for the harmonic mean. The function is HARMEAN(number 1, [number 2]…).[6]
To select the function, begin typing “=HARMEAN” into a blank cell of the spreadsheet, then double-click on the function when it pops up.- For example, type “=HARMEAN” into cell A5 of your spreadsheet and double-click on the function.
-
3
Highlight the cells containing the values you are averaging. Hit the enter key. Excel will calculate the harmonic mean for you and display it in the spreadsheet.
- For example, highlight cells A1-A4 of your spreadsheet and hit enter. Excel will calculate 10.78652 as the harmonic mean.
Advertisement
Add New Question
-
Question
What are the harmonic means of 5, 6 and 7?
3/(1/5+1/6+1/7) = 3/(42/210 + 35/210 + 30/210 ) = 3/( 107/210) = 3 x 210/107= 630/107 = 5.89
-
Question
What is the harmonic mean of x1,x2,x3.xn?
This is just asking for the formula: n/(1/x1 + 1/x2 + 1/x3 +…+1/xn)
-
Question
Can you tell me the harmonic mean of 0 2 4 6?
There’s no harmonic mean when zero is one of the values in the set. That’s because the formula would have 1/0 as one of the terms in the denominator, and 1/0 is infinity and not usable.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate the harmonic meaning, start by determining the number of values in your set of numbers. For example, if you’re working with 10, 12, 16, and 8, you have 4 numbers, so the value is 4. Then, rewrite the numbers you’re working with as denominators over the number 1. For example, if you’re working with 10, 12, 16, and 8, write them as 1/10, 1/12, 1/16, and 1/8. Then, divide 4 by the sum of the fractions to find the harmonic mean. To calculate the harmonic meaning using a calculator, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 147,421 times.
Reader Success Stories
-
Monahil Monahil
Jul 17, 2017
«Very useful and helpful. You must read this article. It is a very simple way of solving problems.»
Did this article help you?
Среднее гармоническое
- Главная
- /
- Математика
- /
- Арифметика
- /
- Среднее гармоническое
Чтобы найти среднее гармоническое нескольких чисел воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Среднее гармоническое:
0
Округление ответа:
Просто введите положительные числа и получите среднее гармоническое этих чисел. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».
Теория
Средним гармоническим H(X1,…,Xn) двух и более чисел является обратная величина к среднему арифметическому их обратных.
Формула
| H(x1,…,xn) | = | n |
| 1⁄x1 + 1⁄x2 + … + 1⁄xn |
Примеры
Для чего служит средняя гармоническая чисел? К примеру, для определения средней скорости:
Среднее гармоническое двух чисел
Представим, что автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути — со скоростью 20 км/ч. И нам надо определить его среднюю скорость. Для этого нам понадобится найти среднее гармоническое для двух чисел: 80 и 20.
| H(80, 20) | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Таким образом, средняя скорость автомобиля равна 32 км/ч.
Среднее гармоническое трех чисел
Если же наш автомобиль треть пути ехал со скоростью 80 км/ч, треть — со скоростью 20 км/ч и треть со скоростью 8 км/ч, то его среднюю скорость определяем так:
H(80, 20,  |
= | 3 | = | 3 | = 16 км/ч |
| 1⁄80 + 1⁄20 + 1⁄8 | 0.0125 + 0.05 + 0.125 |
См. также
Онлайн калькулятор для расчета среднего гармонического двух, трех, четырех и более чисел. Средняя гармоническая величина ( или Среднее гармоническое ) получается от деления числа данных величин на сумму величин обратных данным.
Формулы для нахождения среднего гармонического: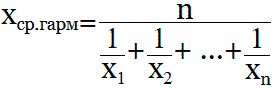 
Формула средней гармонической взвешенной:
×
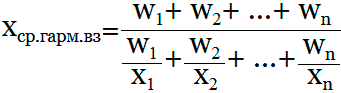
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
Смотрите также
Что такое гармоническое среднее?
Гармоническое среднее — это величина, обратная среднему арифметическому обратных величин, т. е. среднее значение, рассчитанное путем деления количества наблюдений в данном наборе данных на сумму его обратных величин (1/Xi) для каждого наблюдения в данном наборе данных.
Оглавление
- Что такое гармоническое среднее?
- Формула гармонического среднего
- Примеры
- Пример №1
- Пример #2
- Пример №3
- Использование и актуальность
- Рекомендуемые статьи
Формула гармонического среднего
Гармоническое среднее = n / ∑ [1/Xi]
- Можно видеть, что это обратное нормальное среднее значение.
- Среднее гармоническое для нормального среднего равно ∑ x / n, поэтому, если формула меняется на противоположную, она становится n / ∑ x. Тогда все значения знаменателя, которые нужно использовать, должны быть обратными, т. е. для числителя остается «n», а для знаменателя, значений или наблюдений за ними, нам нужно использовать обратные значения.
- Полученное значение всегда будет меньше среднего или среднего арифметического. Среднее арифметическое Среднее арифметическое означает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений. Подробнее.
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы Excel гармонического среднего здесь — Шаблон Excel для формулы среднего гармонического значения
Пример №1
Рассмотрим набор данных из следующих чисел: 10, 2, 4, 7. Затем вам необходимо рассчитать среднее гармоническое, используя обсуждавшуюся выше формулу.
Решение:
Используйте следующие данные для расчета.
Гармоническое среднее = n / ∑ [1/ Xi ]
= 4/(1/10 + 1/2 + 1/4 + 1/7)
= 4 / 0,99
Пример #2
Г-н Виджай является биржевым аналитиком в JP Morgan. Его менеджер попросил его определить коэффициент P/E индекса, который отслеживает цены акций компании W, компании X и компании Y.
Компания W сообщает о доходах в размере 40 миллионов долларов и рыночной капитализации в 2 миллиарда долларов. Компания X сообщает о 3 миллиардах долларов и рыночной капитализации в 9 миллиардов долларов; Компания Y сообщает о прибыли в размере 10 миллиардов долларов и рыночной капитализации в 40 миллиардов долларов. Затем рассчитайте среднее гармоническое для отношения P/E индекса.
Решение:
Используйте следующие данные для расчета.
Во-первых, мы рассчитаем соотношение P/EОтношение P/EОтношение цены к прибыли (PE) измеряет относительную стоимость корпоративных акций, т. е. является ли она недооцененной или переоцененной. Он рассчитывается как отношение текущей цены на акцию к прибыли на акцию. читать далее.
Коэффициент P/E по сути (рыночная капитализацияРыночная капитализацияРыночная капитализация — это рыночная стоимость акций компании, находящихся в обращении. Она рассчитывается как произведение общего количества акций в обращении и цены каждой акции. Подробнее / прибыль).
- P/E компании W = (2 миллиарда долларов) / (40 миллионов долларов) = 50
- P/E компании X = (9 миллиардов долларов) / (3 миллиарда долларов) = 3
- P/E компании Y = (40 миллиардов долларов) / (10 миллиардов долларов) = 4
Расчет значения 1/X
- Компания W = 1/50 = 0,02
- Компания Х= 1/3 = 0,33
- Компания Y= 1/4 = 0,25
Расчет можно сделать следующим образом,
Гармоническое среднее = n / ∑[1/ Xi]
- =3/(1/50 + 1/3 + 1/4)
- =3/0,60
Пример №3
Рей, житель северной Калифорнии, профессиональный спортивный байкер, едет на пляж из своего дома в воскресенье вечером около 17:00 по восточному поясному времени. Он едет на своем спортивном велосипеде со скоростью 50 миль в час в течение 1-й половины пути и со скоростью 70 миль в час во время 2-й половины пути от дома до пляжа. Какова будет его средняя скорость?
Решение:
Используйте следующие данные для расчета.
В этом примере Рей отправился в путешествие с определенной скоростью, и здесь среднее значение будет основано на расстоянии.
Расчет следующий,
Здесь мы можем вычислить среднее гармоническое для средней скорости спортивного мотоцикла Рея.
Гармоническое среднее = n / ∑[1/ Xi]
- =2/(1/50 + 1/70)
- =2/0,03
Средняя скорость спортивного мотоцикла Рея — 58,33.
Использование и актуальность
Гармонические средние, как и другие средние формулы, имеют несколько применений. Они в основном используются в финансах для определенных средних данных, таких как мультипликаторы цен. Например, финансовые мультипликаторы, такие как отношение P/E, не должны усредняться с использованием нормального среднего или среднего арифметического, потому что эти средние значения смещены в сторону больших значений. Можно также использовать гармонические средства для определения определенного типа паттернов, таких как последовательности Фибоначчи, которые маркетологи используют в техническом анализе.
Среднее гармоническое также имеет дело со средними единицами, такими как скорости, отношения или скорость и т. Д. Кроме того, важно отметить, что на него влияют экстремальные значения в данном наборе данных или данном наборе наблюдений.
Среднее гармоническое определено жестко и основано на всех значениях или наблюдениях в данном наборе данных или выборке, и оно может быть пригодным для дальнейшей математической обработки. Как и среднее геометрическое, среднее гармоническое также не сильно зависит от наблюдений или колебаний выборки. Это будет придавать большее значение небольшим значениям или небольшим наблюдениям, и это будет полезно только тогда, когда этим небольшим значениям или этим небольшим наблюдениям необходимо придать больший вес.
Рекомендуемые статьи
Эта статья была руководством по гармоническому среднему и его определению. Здесь мы обсудим формулу для расчета среднего гармонического, а также примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:
- МЕДИАНА Формула ExcelMEDIAN Функция ExcelMEDIAN в Excel дает медиану заданного набора чисел. МЕДИАНА Определяет расположение центра группы чисел в статистическом распределении.Подробнее
- ФормулаФормулаУравнение средневзвешенного значения — это статистический метод, определяющий среднее значение путем умножения весов на их соответствующее среднее значение и получения его суммы. Это среднее значение, в котором веса присваиваются отдельным значениям, определяющим относительную важность каждого наблюдения. Средневзвешенное значение = ∑ni=1 (xi*wi)/∑ni=1wi подробнее о Средневзвешенное значение
- Среднее по сравнению с медианнымСреднее по сравнению с. MedianMean — это среднее значение заданных чисел. Он суммирует числа и делит их на количество чисел, которое дает нам среднее значение. С другой стороны, медиана возвращает среднее число из всего набора данных.Подробнее
- Медиана Формула МедианаФормула медианы в статистике используется для определения среднего числа в наборе данных, упорядоченном в порядке возрастания. Медиана = {(n+1)/2}поток больше