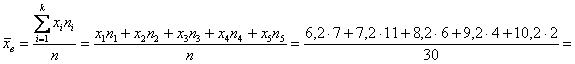Как оценить среднее значение и медиану любой гистограммы
17 авг. 2022 г.
читать 2 мин
Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
По оси X гистограммы отображаются интервалы значений данных, а по оси Y указано, сколько наблюдений в наборе данных приходится на каждый интервал.
Хотя гистограммы полезны для визуализации распределений, не всегда очевидно, что представляют собой средние и медианные значения, просто взглянув на гистограммы.
И хотя невозможно найти точное среднее и срединное значения распределения, просто взглянув на гистограмму, можно оценить оба значения. В этом руководстве объясняется, как это сделать.
Как оценить среднее значение гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку среднего значения любой гистограммы:
Наилучшая оценка среднего: Σm i n i / N
куда:
- m i : середина i -го бина
- n i : частота i -го бина
- N: общий размер выборки
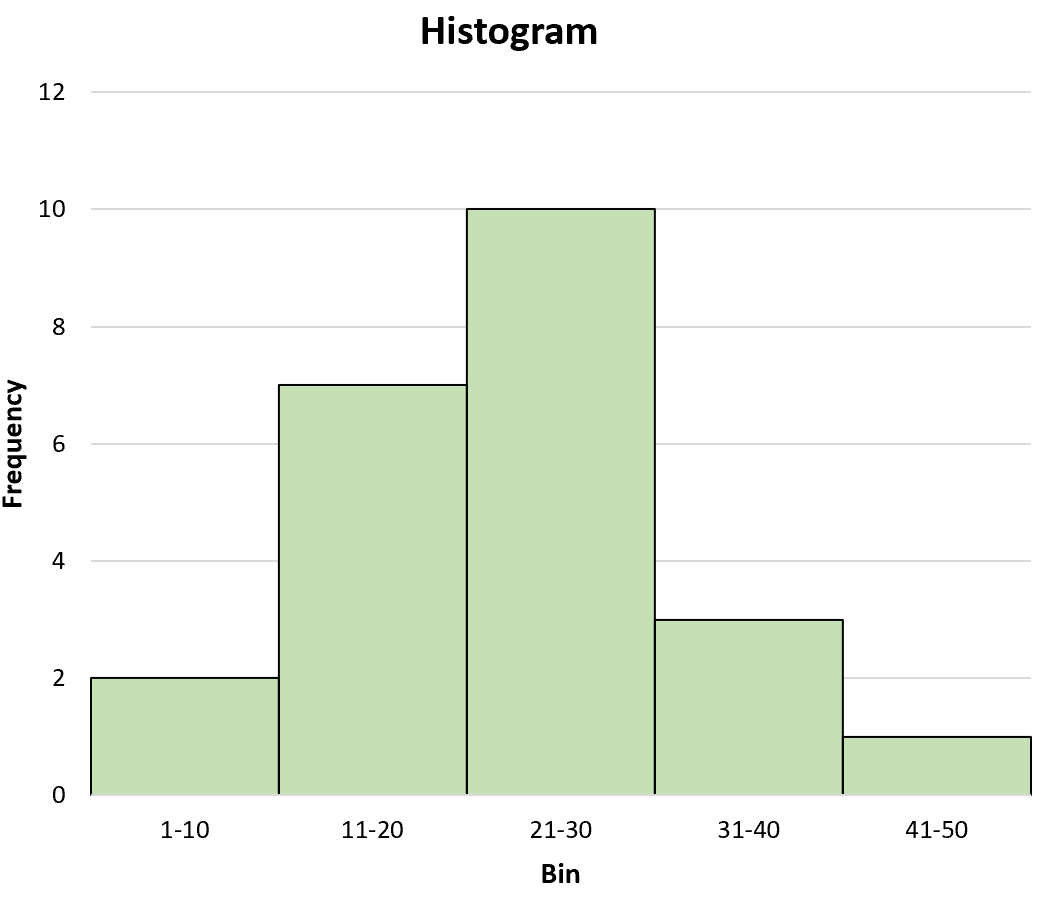
Например, рассмотрим следующую гистограмму:
Наилучшей оценкой среднего значения будет:
Среднее значение = (5,5*2 + 15,5*7 + 25,5*10 + 35,5*3 + 45,5*1) / 23 = 22,89 .
Глядя на гистограмму, это кажется разумной оценкой среднего значения.
Как оценить медиану гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку медианы любой гистограммы:
Наилучшая оценка медианы: L + ((n/2 – F)/f) * w
куда:
- L: Нижний предел средней группы
- n: общее количество наблюдений
- F: кумулятивная частота до средней группы
- f: частота срединной группы
- w: ширина срединной группы
Еще раз рассмотрим следующую гистограмму:
Наилучшей оценкой медианы будет:
Медиана = 21 + ((25/2 – 9)/10) * 9 = 24,15 .
Глядя на гистограмму, это также кажется разумной оценкой медианы.
Связанный: Как оценить стандартное отклонение любой гистограммы
Дополнительные ресурсы
Как найти среднее значение, медиану и моду в диаграммах «стебель-и-листья»
Как рассчитать среднее значение из таблиц частот
Когда использовать среднее значение против медианы
3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?
Начнём опять с ситуации, когда нам даны первичные статические данные:
Пример 10
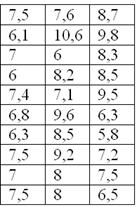
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):
– это в точности числа из Примера 6. Но теперь нам нужно найти среднюю, моду и медиану.
Решение: чтобы найти среднюю по первичным данным, нужно
просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.
Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то,
конечно, забиваем в любую свободную ячейку:
=СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.
Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел
одинаковые, но среди них запросто может найтись так 5-6-7 вариант с одинаковой максимальной частотой, например, частотой 2.
Поэтому модальное значение рассчитывается по сформированному интервальному ряду (см. ниже).
Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем
скобку ) и жмём Enter: . Причём, здесь даже ничего
не нужно сортировать.
Но в Примере 6 я проводил сортировку совокупности по возрастанию (вспоминаем и сортируем), и это хорошая возможность
повторить формальный алгоритм отыскания медианы.
Делим объём выборки пополам:
, и поскольку она состоит из чётного
количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного
ряда:
ден. ед.
Ситуация вторая. Когда даны не первичные данные, а готовый интервальный ряд (что в учебных задачах бывает чаще).
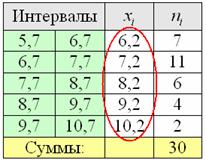
Продолжаем анализировать этот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины интервалов:
– чтобы воспользоваться знакомой формулой дискретного случая:
– и это отличный результат! Расхождение с
более точным значением (), вычисленным по
первичным данным, составило всего 0,04!
Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось
весьма эффективным. Впрочем, с современными программами не составляет особого труда вычислить точное значение даже по
очень большому массиву первичных данных. Если они нам известны 
С другими центральными показателями всё занятнее.
Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в нашей задаче
это интервал с частотой 11, и воспользоваться
следующей страшненькой формулой:
, где:
– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.
Таким образом:
ден. ед. – как видите, «модная» цена на
ботинки заметно отличается от среднего арифметического значения .
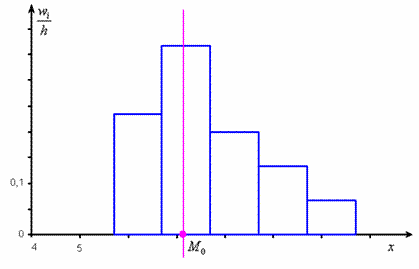
Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот
и отмечу :
откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала
с бОльшей частотой. По той причине, что дешёвых ботинок больше. И, возможно, они тоже вполне себе модные.
Справочно остановлюсь на редких случаях:
– если модальный интервал крайний, то либо
;
– если обнаружатся два смежных модальных интервала, например, и
,
то рассматриваем модальный интервал , при этом
близлежащие интервалы (слева и справа) по возможности тоже укрупняем в два раза;
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым две
или бОльшее количество мод.
Вот такой вот депеш мод 
И медиана. Она рассчитывается чуть по менее страшной формуле. Для её применения
нужно найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две
равные части.
Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты
, здесь же сподручнее рассчитать
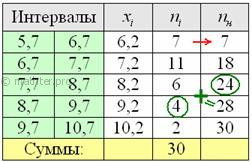
«обычные» накопленные частоты . Вычислительный
алгоритм такой же – первое значение сносим слева (красная стрелка), а каждое следующее получается как сумма
предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):
Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопится» на всех «пройденных»
интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит -ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .
Формула медианы:
, где:
– объём статистической совокупности;
– нижняя граница медианного
интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота
предыдущего интервала.
Таким образом:
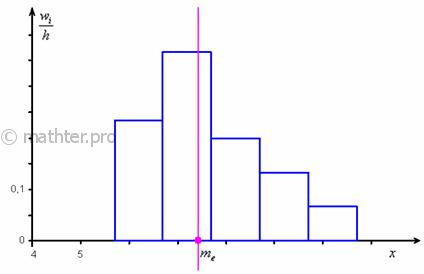
ден. ед. – заметим, что медианное
значение, в отличие от моды, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:
Справочно особые случаи:
– если медианным является крайний левый интервал, то ;
– если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то
объединяем эти интервалы, и по возможности удваиваем предыдущий интервал.
Ответ: ден. ед.
По сравнению с предыдущей задачей ,
центральные показатели оказались заметно отличны друг от друга. Это говорит об асимметрии
(«скошенности») распределения цен, что хорошо видно по гистограмме и совершенно логично –
ботинок низкого и среднего ценового сегмента много, а премиального – мало.
Задание для тренировки:
Пример 11
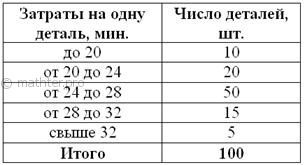
Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено
следующее статистическое распределение:
…да, тот самый завод Петровского 
Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на
калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце книги. Это, кстати, уже
каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.
Что ещё можно сказать по теме?
Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные
совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и
медиана плохо характеризуют положение дел.
В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с
помощью перцентилей.
Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Из чего
автоматически следует, что 2-я квартиль – есть в точности медиана: .
В тяжёлых случаях проводится разбиение на 10 частей – децилями – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по
количеству вариант) частей.
И в очень тяжелых случаях в ход пускается 99 перцентилей .
После разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние и другие
показатели.
В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для
самостоятельного изучения.
Ну а сейчас мы переходим к изучению второй группы статистических показателей:


| Оглавление |
Как определить подходящую меру центральной тенденции?
Время на прочтение
6 мин
Количество просмотров 5.2K

Мера центральной тенденции (measure of central tendency) представляет из себя статистическую величину, которая характеризует целый набор данных одним единственным числом. Ее также называют мерой центрального расположения (measure of central location). Она описывает, как выглядит приблизительный центр набора данных.
Но сам по себе термин “центр” может подразумевать немного разные значения в зависимости от конкретной ситуации. Вы можете считать “центром” среднее арифметическое. Вы также можете назвать “центром” данные, которые просто находятся в середине вашей выборки. А еще вы можете рассматривать в качестве “центра” данные, которые повторяются чаще всего. Все эти центры по-своему характеризуют ваши данные.
Поскольку человеческое понимание “центра” может разниться, статистика позаботилась определить каждый вариант. Таким образом мы имеем следующие общепринятые меры центральной тенденции:
-
Среднее арифметическое.
-
Медиана.
-
Мода.
В этой статье я расскажу, каким образом распределение вашего набора данных играет роль в выборе подходящей меры центральной тенденции. А объяснять я буду это на примере реальных наборов данных.
1. Среднее арифметическое
Среднее арифметическое — это среднее значение всех элементов в наборе данных. Оно рассчитывается как сумма всех значений, деленная на общее количество значений.
Среднее арифметическое = сумма всех значений / общее количество значений
Когда следует использовать среднее арифметическое?
Среднее арифметическое лучше всего использовать для описания данных, которые имеют нормальное распределение. Нормальное распределение — это когда построив график по “значениям” и их “частоте” (количеству появлений каждого значения в наборе данных), вы получаете кривую, по форме напоминающую колокол. Центр этой кривой совпадает со средним арифметическим.
Пример — набор данных с длинами крыльев комнатной мухи
В качестве примера я буду использовать реальный набор данных — это набор данных с длинами крыльев комнатной мухи, который естественным образом имеет нормальное распределение.
Источник набора данных: [Sokal, R.R. and F.J. Rohlf, 1968. Biometry, Freeman Publishing Co., p 109. Original data from Sokal, R.R. and P.E. Hunter. 1955. A morphometric analysis of DDT-resistant and non-resistant housefly strains Ann. Entomol. Soc. Amer. 48: 499-507.]
Набор данных содержит длины крыльев комнатной мухи в миллиметрах. В нем 100 элементов.
Я построил гистограмму (по “значениям” и “количествам повторений этих значений”) этих данных, которую вы можете наблюдать ниже. Если мы проведем по внешним краям столбцов плавную линию, то она образует колоколообразную кривую. Вычислив среднее арифметическое значение этих данных, мы получим 45,5. А теперь давайте поищем на приведенном ниже графике полученное значение 45,5. Он находится прямо по середине.
Колоколообразная кривая со средним значением в центре дает нам четкое понимание, что этот набор данных имеет нормальное распределение.
import numpy as np
import matplotlib.pyplot as plt
data_housefly = np.loadtxt("housefly_wing_length.txt")
plt.hist(data_housefly)
plt.xlabel("Wing length")
plt.ylabel("Number of occurences")
plt.title("Histogram - Housefly wing lengths")
plt.show()Это хороший пример, наглядно демонстрирующий, что для нормально распределенных данных имеет смысл использовать “среднее арифметическое” как меру центральной тенденции.
Когда НЕ стоит использовать среднее арифметическое?
Хотя среднее арифметическое является одной из основных мер центральной тенденции, иногда (на самом деле очень часто) оно наоборот может ввести вас в заблуждение. Данные из реального мира не всегда имеют нормальное распределение. В подавляющем большинстве случаев есть вероятность, что ваши данные ассиметричны.
Ассиметричные данные — это данные, в которых несколько элементов у верхнего или нижнего пределов имеют заметно отличающийся паттерн по сравнению с остальной частью набора данных.
Пример — набор данных с зарплатами игроков NBA
Давайте посмотрим на набор данных с зарплатами игроков NBA. Этот набор данных содержит зарплаты в долларах США за период с 2017 по 2018 годы.
Я построил гистограмму столбца c зарплатой (название столбца “season17_18”).
import numpy as np
import matplotlib.pyplot as plt
data_nba = pd.read_csv("NBA_player_salary.csv")
plt.hist(data_nba.season17_18)
plt.xlabel("Salary in US Dollars")
plt.ylabel("Number of occurrences")
plt.title("NBA Player Salary - Histogram")
plt.show()Глядя на приведенное выше распределение, становится очевидным, что данные распределены не нормально. Из 573 игроков более 300 получают зарплату ниже 2,5 миллионов долларов (из графика выше). Но когда мы вычисляем среднее арифметическое заработной платы, оно составляет 5,85 миллиона долларов.
Как вы считаете, годится ли среднее арифметическое в качестве лучшего представления этих данных в целом?
Уж точно нет. Те немногие игроки, которые получали огромные зарплаты, утащили среднее арифметическое далеко от центра. Это называется асимметрией данных.
Не имеет смысла и говорить о том, что среднее арифметическое, которое составляет 5,85 миллиона, является центром, потому что абсолютное большинство из игроков получили зарплату менее 2,5 миллиона долларов.
Таким образом, в случае подобных асимметрий наборов данных среднее арифметическое хорошим выбором для представления данных не является. Здесь нам может помочь медиана.
2. Медиана
Медиана — это значение, которое находится в центре (прямо посередине), если данные расположены в порядке возрастания или убывания.
Если общее количество значений в наборе данных нечетное, то в центральной позиции будет только одно число. Это и будет наша медиана. Если общее количество значений в наборе данных четное, в центральной позиции будет два значения. В этом случае медиана представляет собой среднее значение этих двух значений.
Когда следует использовать медиану?
Если набор данных асимметричен или содержит выбросы, среднее арифметическое — не лучший способ представления данных. В таком случае как меру центральной тенденции можно использовать медиану. Выбросы не портят медиану. Потому что само название “выбросы” означает, что они располагаются снаружи, либо в нижнем, либо в верхнем диапазоне. В таком случае медиана — это среднее значение, не нарушенное выбросами.
Еще раз давайте рассмотрим ассиметричный набор данных с зарплатами игроков NBA. (Который мы рассматривали в предыдущем разделе “Когда НЕ стоит использовать среднее арифметическое?”). Медиана по зарплате составляет 2,38 миллиона долларов.
Это значение находится в первой столбце. Обратите внимание, что ось X это 10^7. Итак, первый столбик представляет зарплату до 2,5 миллионов. Таким образом, медианное значение 2,38 миллиона лучше всего представляет эти данные, потому что большинство игроков получают зарплату, близкую к этому показателю.
Когда НЕ стоит использовать медиану?
Если и среднее арифметическое, и медиана одного и того же набора данных не сильно отклоняются, то можно использовать обе эти меры. В любом случае расчет среднего арифметического предполагает учет всех элементов данных и их усреднение. Таким образом, логичнее, что среднее арифметическое является более точной мерой (когда среднее арифметическое и медиана не сильно отклоняются).
Как определить, является ли ваш набор данных асимметричным или содержит выбросы?
Самый банальный способ определить, является ли ваш набор данных асимметричным или содержит выбросы, — это вычислить среднее арифметическое и медиану. Если обе меры не сильно отклоняются, то с вашим набором данных все в порядке. И вы сэкономили время, которое в противном случае было бы потрачено на очистку и преобразование данных.
Если среднее арифметическое и медиана очень сильно отклоняются, ваш набор данных асимметричен или содержит выбросы. Следующий шаг — провести исследование с целью выявить и удалить выбросы, если таковые имеются. Или применить какое-либо преобразование, чтобы уменьшить асимметрию в ваших данных, если таковая имеется.
3. Мода
Мода — это значение, которое чаще всего встречается в наборе данных. В гистограмме мода — это значение с самым высоким столбцом.
Если набор данных имеет более одного значения с одинаковой максимальной частотой появления, набор данных имеет мультимодальное распределение, поскольку он имеет несколько мод. Если в наборе данных нет повторяющихся значений, то и моды у него тоже нет.
Когда стоит использовать моду?
Моду можно использовать для анализа часто встречающихся значений как числовых, так и категориальных данных.
Мода — единственная мера центральной тенденции, которую можно использовать с категориальными данными. Для категориальных данных вы не можете вычислить среднее арифметическое или медиану. Мода — единственный выбор в таких случаях.
Пример — Простое перечисление
Ниже приведен учебный набор данных, отражающий любимый вид искусства семерых человек. Построим частотный график (гистограмму).
data_art = [‘music’, ‘painting’, ‘pottery’, ‘painting’, ‘dance’, ‘music’, ‘music’]
import matplotlib.pyplot as plt
data_art = ['music', 'painting', 'pottery', 'painting', 'dance', 'music', 'music']
plt.hist(data_art)
plt.xlabel("Favorite art")
plt.ylabel("Number of occurrences")
plt.title("Histogram of favorite art")
plt.show()Во многих областях машинного обучения возникают функции многих переменных и их производные. Такие производные ещё называют «матричными». На открытом уроке мы поговорим про отличие таких производных от обычных, изучаемых в школе, разберём необходимую теорию, научимся такие производные считать, а также посмотрим, где и как матричные производные используются. Регистрация открыта по ссылке для всех желающих.