Простая формула, чтобы подсчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
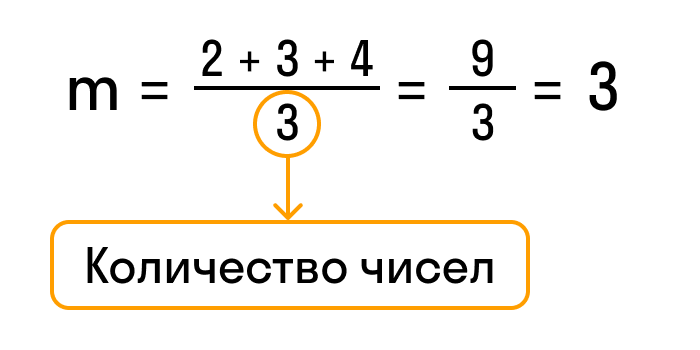
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
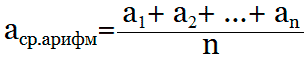
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
http://allcalc.ru/node/1830
http://100urokov.ru/predmety/urok-11-uravneniya-irracionalnye
Содержание
- Простая формула, чтобы подсчитать среднее арифметическое
- Понятие среднего арифметического
- Примеры расчета среднего арифметического
- Среднее арифметическое
- Содержание
- Знакомство со средним арифметическим
- Задачи на нахождение среднего арифметического
- Среднее арифметическое десятичных дробей
- Среднее арифметическое обыкновенных дробей
- Найти среднее арифметическое действительных корней трех квадратных уравнений
- Простая формула, чтобы подсчитать среднее арифметическое
- Понятие среднего арифметического
- Примеры расчета среднего арифметического
- Среднее арифметическое
- Содержание
- Знакомство со средним арифметическим
- Задачи на нахождение среднего арифметического
- Среднее арифметическое десятичных дробей
- Среднее арифметическое обыкновенных дробей
Простая формула, чтобы подсчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Источник
Среднее арифметическое
Содержание
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому – тому, что это такое, как находится и где может пригодиться.
Знакомство со средним арифметическим
Решавр, Вообразавр и Иксератопс собирали грибы. Решавр нашёл $5$ грибов, Вообразавр – $7$, а Иксератопс целых $9$! Друзья решили разделить найденное количество грибов поровну.
Они сложили все грибы в кучку, а потом каждый взял себе равное число грибов, то есть они поделили общее количество на $3$.
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 cdot 2 + 60 + 100 cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
На рисунке 3 изображены три отрезка. Длина отрезка АВ $5.9$ см, отрезка CD – $7.3$ см, а отрезок EF равен среднему арифметическому первых двух отрезков. Какова длина отрезка EF?
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
Теперь решим задачу на нахождение слагаемых. Два кролика ели морковку, серый кролик съел в $1.4$ раза больше морковки, чем белый. Сколько морковки съел каждый, если среднее количество съеденного – $7.5$ морковок?
Начинаем «распутывать» наш пример. Если мы знаем, что среднее арифметическое двух чисел – $7.5$, значит, их сумма – $7.5 cdot 2 = 15$
Примем количество съеденного белым кроликом за $x$, тогда серый съел $1.4 cdot x$. Можно составить уравнение:
$$1.4 cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Сначала найдём значение выражения.
$$1.4 cdot x + x = 2.4 cdot x = 15$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
Значит, наше решение было верным.
Среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Найдём среднее арифметическое дробей $frac<2><3>$ и $frac<4><7>$.
Мы можем выполнить сложение только в том случае, если у обоих слагаемых будет одинаковый знаменатель. Сначала нужно понять, к какому наименьшему общему знаменателю нужно привести эти дроби. Для этого требуется найти число, которое делится и на $3$, и на $7$. Это число будет называться НОК (наименьшее общее кратное). Для чисел $3$ и $7$ это будет произведение этих чисел, $21$.
Для того чтобы вычислить дополнительные множители, нужно разделить НОК на каждый из знаменателей. Таким образом, для $3$ дополнительным множителем будет $7$, а для $7$ это будет $3$.
Умножаем обе части дроби на один и тот же дополнительный множитель.
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
Эту дробь можно сократить, разделив обе части на $2$. У нас получится $frac<13><21>$.
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Разберём ещё пример со смешанными дробями. Найдём среднее арифметическое для дробей $2frac<1><6>$ и $3frac<1><15>$.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
Теперь приведём эти дроби к общему знаменателю. НОК $(15$ и $6) = 30$
Теперь подбираем дополнительные множители и складываем наши дроби.
Мы могли бы выделить целую часть из этой дроби, но нет необходимости, так как мы не закончили вычисления. Для нахождения среднего арифметического разделим полученное число на $2$ (другими словами, умножим дробь на число, обратное делителю, в данном случае $frac<1><2>$).
Если мы захотим поделить $37$ на $60$, у нас получится периодическая дробь: $0.61(6) $
Если нужно записать ответ в виде десятичной дроби, то можно использовать периодическую дробь. В некоторых случаях можно округлить эту дробь, например, $0.61(6) $ приблизительно равно $0.62$
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Источник
Найти среднее арифметическое действительных корней трех квадратных уравнений
Вычисление корней квадратных уравнений
Здравствуйте! Решил попрактиковаться в с++ и написать некое подобие калькулятора, сделал меню.

Нужно найти среднее арефметическое трех квадратов чисел a, b, c
Сделать масивом.Дано 5 действительных чисел. Вычислить сумму квадратных корней модулей этих чисел
Дано 5 действительных чисел. Вычислить сумму квадратных корней модулей этих чисел

Выясните, что больше: среднее арифметическое или среднее геометрическое трех положительных чисел.
22.02.2015, 10:00 Найти среднее арифметическое действительных корней трех квадратных уравнений
Напрасно кропал свои вирши
Товарищ Виет
Он был неплохой математик,
Но слабый поэт
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Всем здрасте помогите плиз. Дается два вещественных числа. Найти среднее арифметическое их.
Среднее арифметическое трех чисел
Нужно создать программу в которой вводятся 3 числа и находится среднее арифметическое. Результат.
Найти количество действительных корней квадратного уравнения
не могу найти ошибку.Компилятор ругается Суть задачи : Определить кол-во действительных корней.

Короче препод в универе задал на дом задания .А суть такова : вводишь любые три числа ,если же.
Источник
Простая формула, чтобы подсчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Источник
Среднее арифметическое
Содержание
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому – тому, что это такое, как находится и где может пригодиться.
Знакомство со средним арифметическим
Решавр, Вообразавр и Иксератопс собирали грибы. Решавр нашёл $5$ грибов, Вообразавр – $7$, а Иксератопс целых $9$! Друзья решили разделить найденное количество грибов поровну.
Они сложили все грибы в кучку, а потом каждый взял себе равное число грибов, то есть они поделили общее количество на $3$.
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 cdot 2 + 60 + 100 cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
На рисунке 3 изображены три отрезка. Длина отрезка АВ $5.9$ см, отрезка CD – $7.3$ см, а отрезок EF равен среднему арифметическому первых двух отрезков. Какова длина отрезка EF?
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
Теперь решим задачу на нахождение слагаемых. Два кролика ели морковку, серый кролик съел в $1.4$ раза больше морковки, чем белый. Сколько морковки съел каждый, если среднее количество съеденного – $7.5$ морковок?
Начинаем «распутывать» наш пример. Если мы знаем, что среднее арифметическое двух чисел – $7.5$, значит, их сумма – $7.5 cdot 2 = 15$
Примем количество съеденного белым кроликом за $x$, тогда серый съел $1.4 cdot x$. Можно составить уравнение:
$$1.4 cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Сначала найдём значение выражения.
$$1.4 cdot x + x = 2.4 cdot x = 15$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
Значит, наше решение было верным.
Среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Найдём среднее арифметическое дробей $frac<2><3>$ и $frac<4><7>$.
Мы можем выполнить сложение только в том случае, если у обоих слагаемых будет одинаковый знаменатель. Сначала нужно понять, к какому наименьшему общему знаменателю нужно привести эти дроби. Для этого требуется найти число, которое делится и на $3$, и на $7$. Это число будет называться НОК (наименьшее общее кратное). Для чисел $3$ и $7$ это будет произведение этих чисел, $21$.
Для того чтобы вычислить дополнительные множители, нужно разделить НОК на каждый из знаменателей. Таким образом, для $3$ дополнительным множителем будет $7$, а для $7$ это будет $3$.
Умножаем обе части дроби на один и тот же дополнительный множитель.
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
Эту дробь можно сократить, разделив обе части на $2$. У нас получится $frac<13><21>$.
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Разберём ещё пример со смешанными дробями. Найдём среднее арифметическое для дробей $2frac<1><6>$ и $3frac<1><15>$.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
Теперь приведём эти дроби к общему знаменателю. НОК $(15$ и $6) = 30$
Теперь подбираем дополнительные множители и складываем наши дроби.
Мы могли бы выделить целую часть из этой дроби, но нет необходимости, так как мы не закончили вычисления. Для нахождения среднего арифметического разделим полученное число на $2$ (другими словами, умножим дробь на число, обратное делителю, в данном случае $frac<1><2>$).
Если мы захотим поделить $37$ на $60$, у нас получится периодическая дробь: $0.61(6) $
Если нужно записать ответ в виде десятичной дроби, то можно использовать периодическую дробь. В некоторых случаях можно округлить эту дробь, например, $0.61(6) $ приблизительно равно $0.62$
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Источник
План урока:
Арифметический квадратный корень
Вычисление квадратного корня
Функция квадратного корня
Свойства арифметического квадратного корня
Преобразование выражений с квадратными корнями
Арифметический квадратный корень
Рассмотрим задачу. Нам известно, что длина квадрата равна 14 см. Какова площадь этого квадрата? Из курса геометрии мы знаем, что для ответа на вопрос надо просто умножить сторону саму на себя, то есть возвести ее в квадрат:
S = 14•14 = 196 см2
Теперь рассмотрим обратную задачу. Известно, что площадь квадрата равна 196 см2. Чему равна длина его стороны? Очевидно, что она составляет 14 см. Для нахождения ответа мы произвели действие, обратное возведению во вторую степень. В математике оно называется извлечением квадратного корня, а само число 14 – квадратным корнем из 196.
Так, 5 – это квадратный корень из числа 25, так как
52 = 25
Очень часто квадратный корень является не целым, а дробным числом. Так, корень из 2 примерно равен 1,414213562 (способы вычисления значения корня будут рассмотрены в этом же уроке, но позже).
Отметим, что порою можно указать для числа не один, а сразу два квадратных корня. Они будут отличаться своим знаком, но совпадать по абсолютной величине (модулю). Так число (–5) также является квадратным корнем из 25:
(– 5)2 = – 5•(– 5) = 25
Вообще у любого положительного числа есть 2 квадратных корня, у любого отрицательного числа их вообще нет, и только у нуля есть единственное значение корня – сам нуль. Докажем это.
Пусть есть произвольное число а, для которого надо вычислить квадратный корень. Обозначим этот корень как х. Тогда по определению можно составить уравнение:
х2 = а
Попробуем решить его с помощью графиков. Для этого построим отдельные графики для левой и правой части равенства. Оба графика, и у = а, и у = х2, мы уже строили в 7 классе. В итоге получаем три случая:
Видно, что при а> 0 графики пересекаются в 2 точках, то есть существует два квадратных корня, которые отличаются лишь своими знаками.
Для определенности математики ввели понятие арифметического квадратного корня.
Ещё раз уточним, что у числа может быть два квадратных корня. Например, у числа 25 это –5 и 5:
(– 5)2 = 25
52 = 25
Арифметическим же называют тот квадратный корень, у которого НЕТ знака минус.
Существует специальный символ для арифметического квадратного корня, который именуют знаком радикала, или просто знаком корня. Выглядит он так:
Если надо показать, что, например, арифметический квадратный корень (часто говорят просто корень) из 25 равен 5, то получается такая запись:
Под знаком радикала может стоять и выражение, содержащее переменные величины. Для его обозначения используют термин подкоренное выражение. Так, в записи
выражением х2 + 2х + 2 является подкоренным.
Мы уже поняли, что из отрицательного числа невозможно извлечь квадратный корень, ведь каждое действительное число при умножении на само себя становится неотрицательным. Поэтому если под знаком радикала находится отрицательное число, то говорят, что выражение не имеет смысла (так же как и дробное выражение, у которого в знаменателе стоит ноль). Так, бессмысленны выражения:
Если под корнем находиться переменная, то при одних ее значениях выражение с корнем имеет смысл, а при других нет. Так, выражение
при х = 9 имеет значение, равное двум:
Но если х = 4, то получаем бессмысленное выражение:
Изучая понятие иррационального числа, мы уже сталкивались с корнями. Исторически именно корень из 2 стал первым числом, для которого была доказана его иррациональность. Числа, чей квадратный корень является целым числом, называются полными квадратами. Примерами полных квадратов являются:
- 4 (потому что 22 = 4);
- 9 (32 = 9);
- 16 (42 = 16).
Для всех натуральных чисел, не являющихся полными квадратами, можно доказать, что их квадратные корни – это иррациональные числа.
Стоит отметить, что открытие иррациональностей корней изменило представления древних греков о числах и сыграло огромную роль в развитии математики.
Теперь рассмотрим порядок действий в выражениях с корнями. Сначала всегда производятся операции в скобках, потом под знаком радикала, далее происходит возведение в степень, и лишь потом другие арифметические операции. Например, есть выражение
Покажем последовательность действий, выделяя их красным цветом:
Если в ходе вычислений получили корень не из полного квадрата, то его следует оставить как есть, и продолжать вычисления, например:
Одинаковые корни можно складывать и вычитать друг с другом:
Из определения квадратного корня следует очевидное тождество:
Приведем пример с конкретными числами:
Однако здесь важно учитывать, что под знаком радикала не может находиться отрицательное число. Так, некорректной будет запись
так как под радикалом слева стоит отрицательное число. Но допускается такая запись:
потому что под знаком радикала слева стоит положительная величина (– 3)•( – 3) = 9.
Напомним, что модулем числа называется его величина, взятая без учета знака. Для обозначения модуля используются квадратные скобки:
Можно записать следующее тождество, связывающее модуль числа с его корнем:
Например:
Вычисление квадратного корня
Ранее для выполнения арифметических операций мы использовали метод «столбика». А как производить вычисление квадратного корня? Существует несколько приемов, мы рассмотрим простейший из них.
Очевидно, что чем больше число, тем больше и его квадрат. Например, 5 > 4, поэтому и 52> 42. Значит, справедливо и обратное утверждение: чем больше число, тем больше и его квадратный корень.
Убедиться в этом можно и с помощью графика функции у = х2. Будем отмечать на нем числа и их квадратные корни:
Видно, что чем выше на оси Оу располагается число, тем правее на оси Ох находится его квадратный корень.
Зная это свойство, легко оценить значение корня из любого числа. Продемонстрируем это на примере вычисления значение корня из 2. Нам известно, что
1 < 2 < 4
Значит, можно записать следующие неравенства:
Нам удалось определить, что корень из двух находится между единицей и двойкой, то есть
Теперь определим первую цифру после запятой для корня из двух. Будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3 и т. д, до тех пор пока не получим выражение, большее 2:
1,12 = 1,21
1,22 = 1,44
1,32 = 1,69
1,42 = 1,96
1,52 = 2,25
Теперь мы можем записать неравенства:
Получается, что корень имеет значение, находящееся между 1,4 и 1,5, то есть
Попытаемся определить ещё одну цифру после запятой:
1,412 = 1,999396
1,422 = 2,002225
Отсюда следует, что:
Продолжая подобные вычисления, можно вычислить любое количество знаков после запятой:
Конечно, на практике все вычисления выполняются компьютером, а не вручную. Однако программисты стремятся написать программы так, чтобы они работали как можно быстрее, то есть получали результат, выполняя меньшее количество вычислений. Поэтому на практике чаще используется метод бисекции (деления надвое), который отличается большей эффективностью. Для начала нужно найти очевидную оценку корня, например:
Получили, что корень из 2 находится между 1 и 2. Теперь найдем среднее арифметическое этих двух значений:
(1 + 2)/2 = 1,5
Возведем среднее арифметическое в квадрат:
1,52 = 2,25
Теперь мы можем записать неравенство
То есть искомое нами значение находится между 1 и 1,5. Снова найдем среднее этих двух оценок и возведем его в квадрат:
(1 + 1,5)/2 = 1,25
1,252 = 1,5625
Зная это, можем записать:
На каждом следующем шаге вычислений мы будем всё точнее определять оценки корня, при этом вычислений мы делаем не очень много.
Периодически могут встречаться задания, в которых надо грубо оценить значение квадратного корня.
Пример. Сколько целых чисел на координатной прямой располагается между
Решение: Ближайшие к числу 60 полные квадраты – это 64 и 49, поэтому можно записать:
Также можно оценить и корень из 140:
Получаем, что между корнями располагается четыре числа: 8, 9, 10 и 11:
Ответ: 4
Функция квадратного корня
Каждому числу соответствует не более чем 1 арифметический квадратный корень. Поэтому формула
задает функцию. Исследуем ее.
Так как под знаком радикала может находиться лишь неотрицательное число, то областью определения корня является множество всех неотрицательных чисел. Такова же и область допустимых значений.
Построим график квадратного корня по точкам. Для этого вычислим ее значения в нескольких точках (указана точность до 0,1):
График функции квадратного корня будет выглядеть так:
Отметим, что полученная линия чем-то напоминает обычную параболу функции у = х2, которую «положили набок», то есть повернули против часовой стрелки на 90°, а после убрали одну из ветвей:
И это не случайность. Дело в том, что две эти функции являются обратными друг другу. Действительно, пусть с помощью графика параболы мы хотим найти значение величины а2. Стрелки показывают последовательность действий:
Мы должны найти а на оси Ох, построить от найденной точки вертикальную линию до пересечения с графиком, а потом провести горизонтальную линию. Но если нам надо вычислить корень из положительного числа b, то мы должны действовать в обратном порядке: найти b на вертикальной оси, провести горизонтальную линию до пересечения с параболой, и потом опустить перпендикуляр на горизонтальную ось:
Получается, для вычисления обеих функций можно использовать один график! Но, так как традиционно аргумент функции обозначают буквой х, а саму функцию как у, а также ось Ох располагают горизонтально, то для получения графика обратной функции надо буквально повернуть график основной функции так, чтобы оси Ох и Оу поменялись местами:
Действительно, в результате поворота получили уже знакомый график функции корня из х. Осталось лишь правильно переименовать оси и повернуть цифры в привычное положение.
Взаимное расположение этих графиков можно описать и иначе. Они симметричны относительно прямой линии, которую задает график у = х. Ведь если точка имеет координаты (а; b) принадлежит параболе у = х2, то, по определению корня, точка с обратными координатами (b; а) должна лежать на графике корня. Однако две такие точки будут симметричны относительно линии у = х:
Соответственно, симметричны относительно этой прямой и графики обратных функций:
Исключительно для большей наглядности (чтобы была очевидна симметрия, о которой идет речь), повернем эту картинку на 45°:
Свойства арифметического квадратного корня
Для упрощения некоторых выражений необходимо использовать особые правила работы с корнями. Сформулируем первое из них:
Математически это правило записывается так:
Например:
Тождество работает для любого количества множителей, а также в обратную сторону:
Однако следующее преобразование недопустимо:
Дело в том, что под знаком радикала не может быть отрицательное число! Слева под двумя радикалами стоят отрицательные числа, а справа под корнем находится уже положительная величина (– 2)•(– 32) = 64. В результате выражение слева не имеет смысл, а справа – имеет, поэтому знака равенства между ними быть не может.
Докажем это правило. Для этого возведем во вторую степень выражение
Получили, что по определению корня можно записать:
Следующее свойство касается дробей:
Символически это выглядит так:
Приведем примеры использования этого свойства:
Теперь докажем это правило. Можно записать, что
Значит, по определению верно равенство
Третье правило помогает извлекать корень из числа, возведенного в степень:
где а –действительное число (в том числе и отрицательное), а k – натуральное число.
Это тождество помогает выполнить следующие действия:
Стоит обратить внимание, что в последнем случае под корнем НЕ стоит отрицательное число, так как на самом деле (– 2)10 – это положительное число. Вообще при возведении любого числа в четную степень получается неотрицательное число.
Для доказательства этого факта используем то, что
Зная это, можно выполнить преобразования:
Преобразование выражений с квадратными корнями
Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:
Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:
Обратное действие называют внесением множителя под знак корня:
Пример. Какое число больше
Решение. Внесем множитель под знак корня:
Из двух корней больше тот, у которого больше подкоренное выражение, поэтому
Из этого следует, что
Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:
Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:
Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула разности квадратов:
Рассмотрим несколько задач.
Пример. Найдите наибольшее значение выражения
Решение. По формуле разности квадратов можно записать:
Зная это, заменим знаменатель дроби:
Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять
Пример. Упростите выражение
Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида
называют двойным радикалом.
Существует формула двойного радикала, с помощью которой его можно иногда упростить:
Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя формулу квадрата суммы (х ± у)2 = х2 ± 2ху + у2:
Принципиально важно, что величина а2 – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере. Пусть надо освободиться от внешнего радикала в выражении
Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:
Заметим, что формула двойного радикала полезна в том случае, если выражение а2 – b является полным квадратом.
Корнем 






![sqrt[n]{a} LaTeX formula: sqrt[n]{a}](http://helpy.quali.me/uploads/formulas/0731f1cb60d70120cd50c33712908814158a11c5.1.1.png)

![sqrt[n]{a}=b LaTeX formula: sqrt[n]{a}=b](http://helpy.quali.me/uploads/formulas/96af48bf48ccf20f7d0cf82fc7eb2888f038d3ed.1.1.png)



Неотрицательный корень 



![sqrt[4]{0,0016}=0,2 LaTeX formula: sqrt[4]{0,0016}=0,2](http://helpy.quali.me/uploads/formulas/b2820cc61e931dc782c900930237536f267fa8e1.1.1.png)
![sqrt[3]{1000}=10 LaTeX formula: sqrt[3]{1000}=10](http://helpy.quali.me/uploads/formulas/87f0ddfe065f68272fdeca96e8be1fba95b42200.1.1.png)
Если показатель корня четное число, то подкоренное выражение не может быть отрицательным числом, так как четная степень и положительного и отрицательного числа есть число положительное.
Если показатель корня равен числу 





Если показатель корня нечетное число, то подкоренное выражение может быть положительным числом, отрицательным числом и числом 
Если показатель корня равен числу 

![sqrt[3]{a} LaTeX formula: sqrt[3]{a}](http://helpy.quali.me/uploads/formulas/cd52378aeec567084cd19c17b105310b036f04b7.1.1.png)
![sqrt[3]{8}=2 LaTeX formula: sqrt[3]{8}=2](http://helpy.quali.me/uploads/formulas/b45396844cc5f1cdad94a976d7f541914bed3c67.1.1.png)
![sqrt[3]{-64}=-4 LaTeX formula: sqrt[3]{-64}=-4](http://helpy.quali.me/uploads/formulas/80547f1526e955e793acd87b4529b0ce8efe112f.1.1.png)
Свойства корней:
![sqrt[n]{a}sqrt[n]{b}=sqrt[n]{ab}=(ab)^{frac{1}{n}} LaTeX formula: sqrt[n]{a}sqrt[n]{b}=sqrt[n]{ab}=(ab)^{frac{1}{n}}](http://helpy.quali.me/uploads/formulas/c1d329832928d0d095062c82da68203b65f46160.1.1.png)
![sqrt[n]{sqrt[m]{a}}=sqrt[nm]{a}=a^{frac{1}{nm}} LaTeX formula: sqrt[n]{sqrt[m]{a}}=sqrt[nm]{a}=a^{frac{1}{nm}}](http://helpy.quali.me/uploads/formulas/7a0cfc273bc8f860232e53bb118156f8d150b2fd.1.1.png)
![frac{sqrt[n]{a}}{sqrt[n]{b}}=sqrt[n]{frac{a}{b}}=left ( frac{a}{b} right )^{frac{1}{n}} LaTeX formula: frac{sqrt[n]{a}}{sqrt[n]{b}}=sqrt[n]{frac{a}{b}}=left ( frac{a}{b} right )^{frac{1}{n}}](http://helpy.quali.me/uploads/formulas/6b12d2e89b4bf8086f5c0f98d1e5226cf025bbb2.1.1.png)
![sqrt[2n]{a^{2n}}=left | a right | LaTeX formula: sqrt[2n]{a^{2n}}=left | a right |](http://helpy.quali.me/uploads/formulas/cbd9b90891fcdca819ec0b57a22ff56c301c4728.1.1.png)
![sqrt[2n+1]{a^{2n+1}}=a LaTeX formula: sqrt[2n+1]{a^{2n+1}}=a](http://helpy.quali.me/uploads/formulas/48d600dfe62d7c443aa76c00d36eb0047445ab1d.1.1.png)
При четном значении 





Например: 
![sqrt{sqrt[3]{100}}=sqrt[6]{10^2}=sqrt[3]{10} LaTeX formula: sqrt{sqrt[3]{100}}=sqrt[6]{10^2}=sqrt[3]{10}](http://helpy.quali.me/uploads/formulas/8c13e07cb0b67dd03d4fec8d94ffbe7ac35032bd.1.1.png)
![sqrt[4]{3^4}=3 LaTeX formula: sqrt[4]{3^4}=3](http://helpy.quali.me/uploads/formulas/df474d953f8ccfa86f2870908f92f5b8a0640108.1.1.png)
![sqrt[8]{(-9)^8}=left | -9 right |=9 LaTeX formula: sqrt[8]{(-9)^8}=left | -9 right |=9](http://helpy.quali.me/uploads/formulas/3291a64cfed26eb7123ca357020f0ca34c147edd.1.1.png)
![sqrt[7]{(-21)^7}=-21 LaTeX formula: sqrt[7]{(-21)^7}=-21](http://helpy.quali.me/uploads/formulas/a8caf6ca96fb89ab18981f05cb9ca90b7e285404.1.1.png)
Внесение множителя под знак корня
Если показатель корня нечетное число, то для любого числа 

![asqrt[2n+1]{b}=sqrt[2n+1]{a^{2n+1}b} LaTeX formula: asqrt[2n+1]{b}=sqrt[2n+1]{a^{2n+1}b}](http://helpy.quali.me/uploads/formulas/78df90259f8961606c49bd0078eac0976af88219.1.1.png)
Если 
![asqrt[2n+1]{b}=0 LaTeX formula: asqrt[2n+1]{b}=0](http://helpy.quali.me/uploads/formulas/78509f150ba9e24f4f95e8cb72144f514ccbc5ba.1.1.png)
Например, ![-2asqrt[3]{3}=sqrt[3]{-8a^3cdot 3}=sqrt[3]{-24a^3} LaTeX formula: -2asqrt[3]{3}=sqrt[3]{-8a^3cdot 3}=sqrt[3]{-24a^3}](https://helpy.quali.me/uploads/formulas/aa3ebbbabe8c26479f4a657772c1c0d8e9102b43.1.1.png)
Вынесение множителя из-под знака корня
Если показатель корня нечетное число, то справедливо равенство:
![sqrt[2n+1]{a^{2n+1}b}=acdot sqrt[2n+1]{b} LaTeX formula: sqrt[2n+1]{a^{2n+1}b}=acdot sqrt[2n+1]{b}](http://helpy.quali.me/uploads/formulas/7532c710ca04cfe250e5942c69f6624023900386.1.1.png)
Если показатель корня четное число, то справедливо равенство:
![sqrt[2n]{a^{2n}b}=left | a right |cdot sqrt[2n]{b} LaTeX formula: sqrt[2n]{a^{2n}b}=left | a right |cdot sqrt[2n]{b}](http://helpy.quali.me/uploads/formulas/2c92799900ade24a2dbe78dcdac0beeeaf0d71d4.1.1.png)
Например: ![sqrt[3]{a^5b^{15}c^6}=ab^5c^2 cdot sqrt[3]{a^2} LaTeX formula: sqrt[3]{a^5b^{15}c^6}=ab^5c^2 cdot sqrt[3]{a^2}](https://helpy.quali.me/uploads/formulas/c9fc84aa03ccbac45f289e5fb5368c600cfc62b1.1.1.png)

Сравнение выражений, содержащих корни
1. Если 
![sqrt[n]{a}>sqrt[n]{b} LaTeX formula: sqrt[n]{a}>sqrt[n]{b}](http://helpy.quali.me/uploads/formulas/a282355b0461dc1f9cbb239c831ac5ac69d253a7.1.1.png)

2. Если 

![sqrt[n]{a}>sqrt[m]{a} LaTeX formula: sqrt[n]{a}>sqrt[m]{a}](http://helpy.quali.me/uploads/formulas/ef2056d5c24c8cf29ae48fe5c214ec5e2cf3426d.1.1.png)
![sqrt[4]{2}<sqrt{2} LaTeX formula: sqrt[4]{2}<sqrt{2}](http://helpy.quali.me/uploads/formulas/adc145247e4c0a541475a73a1d40dc6d4462e96b.1.1.png)
3. Если 

![sqrt[n]{a}<sqrt[m]{a} LaTeX formula: sqrt[n]{a}<sqrt[m]{a}](http://helpy.quali.me/uploads/formulas/0d670269ad603e4886bf78a55afa8bc169cfab2e.1.1.png)
![sqrt[4]{0,2}>sqrt{0,2} LaTeX formula: sqrt[4]{0,2}>sqrt{0,2}](http://helpy.quali.me/uploads/formulas/4228339478bab96285d02a2ec0c61dd58732415b.1.1.png)
4. Чтобы сравнить числа ![sqrt[m]{a} LaTeX formula: sqrt[m]{a}](http://helpy.quali.me/uploads/formulas/501e9a776a4845d0b53e8cc1300a46eea417b8d5.1.1.png)
![sqrt[n]{b} LaTeX formula: sqrt[n]{b}](http://helpy.quali.me/uploads/formulas/2e7817394a53bbc1f946448dff14f022f6adeb83.1.1.png)
5. Чтобы сравнить числа 
![sqrt[n]{b} LaTeX formula: sqrt[n]{b}](http://helpy.quali.me/uploads/formulas/2e7817394a53bbc1f946448dff14f022f6adeb83.1.1.png)



![sqrt[n]{a^n} LaTeX formula: sqrt[n]{a^n}](http://helpy.quali.me/uploads/formulas/42d5f00bbffdd213c6a893ebaf1093be9dc7596a.1.1.png)
Степень с действительным показателем
Степени с действительным показателем обладают всеми свойствами степеней с целым показателем. При этом следует помнить, что:
а) степень числа с натуральным показателем имеет смысл для любого основания, так как эта степень определяется с помощью операции умножения;
б) степень с целым отрицательным показателем имеет смысл для любого основания, кроме основания 
в) степень с рациональным показателем определяется с помощью операции извлечения корня, которая всегда выполнима, если основание степени положительное число и не всегда выполнима, если основание степени отрицательное число;
г) степень с любым действительным показателем всегда определена, если ее основание – положительное число.
Среднее арифметическое и среднее геометрическое
Чтобы найти среднее арифметическое нескольких чисел необходимо сумму этих чисел разделить на их количество.
Например, среднее арифметическое чисел 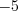



Чтобы найти среднее геометрическое двух положительных чисел, необходимо извлечь корень второй степени из произведения этих чисел. Чтобы найти среднее геометрическое 





![sqrt[4]{3cdot 6cdot 9cdot 8}=sqrt[4]{3cdot 3cdot 9cdot 16}=3cdot 2=6 LaTeX formula: sqrt[4]{3cdot 6cdot 9cdot 8}=sqrt[4]{3cdot 3cdot 9cdot 16}=3cdot 2=6](http://helpy.quali.me/uploads/formulas/32f3b7c81b5ca667fb191c793347379ed15fff77.1.1.png)
Пример 1. Найдите значение выражения ![frac{sqrt[4]{3}}{sqrt{sqrt{48}}}-left ( -0,5^0 cdot sqrt[6]{(-2)^6} right )^2 LaTeX formula: frac{sqrt[4]{3}}{sqrt{sqrt{48}}}-left ( -0,5^0 cdot sqrt[6]{(-2)^6} right )^2](https://helpy.quali.me/uploads/formulas/4190795f22cf624088f5cad8559bec3af54c4771.1.1.png)
Решение. Применяя формулы 1.17 и 1.18, получим 
Ответ: 
Пример 2. Упростите выражение ![frac{sqrt[4]{-16a^4b^5}}{2b} LaTeX formula: frac{sqrt[4]{-16a^4b^5}}{2b}](http://helpy.quali.me/uploads/formulas/8aa72d032eca758cbee319cffd85570a559acbc1.1.1.png)
Решение. Применяя формулу 1.23, получим ![frac{sqrt[4]{-16a^4b^5}}{2b}=frac{2left | a right |cdot left | b right |sqrt[4]{-b}}{2b}=frac{-bleft | a right |sqrt[4]{-b}}{b}=-left | a right |sqrt[4]{-b} LaTeX formula: frac{sqrt[4]{-16a^4b^5}}{2b}=frac{2left | a right |cdot left | b right |sqrt[4]{-b}}{2b}=frac{-bleft | a right |sqrt[4]{-b}}{b}=-left | a right |sqrt[4]{-b}](http://helpy.quali.me/uploads/formulas/c5568793ab79dd8bf8762f2ed67bda449bff57c8.1.1.png)
Ответ: ![-left | a right |sqrt[4]{-b} LaTeX formula: -left | a right |sqrt[4]{-b}](http://helpy.quali.me/uploads/formulas/fc6cff9beb84957618f8a6166b144af5d3a855ca.1.1.png)
Пример 3. Сравните числа: 

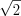
![sqrt[3]{3} LaTeX formula: sqrt[3]{3}](http://helpy.quali.me/uploads/formulas/e2815fa9ade5a36cd9af6c76c1ee2a7005f48271.1.1.png)
Решение. 1. Так как 



2. Так как ![sqrt{2}=sqrt[6]{2^3}=sqrt[6]{8} LaTeX formula: sqrt{2}=sqrt[6]{2^3}=sqrt[6]{8}](http://helpy.quali.me/uploads/formulas/ace719487b9f8f7b1cc8744798615cff9fabe75b.1.1.png)
![sqrt[3]{3}=sqrt[6]{3^2}=sqrt[6]{9} LaTeX formula: sqrt[3]{3}=sqrt[6]{3^2}=sqrt[6]{9}](http://helpy.quali.me/uploads/formulas/7bc52af9ce0947c4f1625de92859345fc124d016.1.1.png)
![sqrt[6]{8}<sqrt[6]{9} LaTeX formula: sqrt[6]{8}<sqrt[6]{9}](http://helpy.quali.me/uploads/formulas/81a9e197820ba14afafd85cd3379cca3a376928d.1.1.png)
![sqrt{2}<sqrt[3]{3} LaTeX formula: sqrt{2}<sqrt[3]{3}](http://helpy.quali.me/uploads/formulas/b028b6427d1d3c2b5059fbd2e041c2272c75af5a.1.1.png)
Пример 4. Упростите выражение ![frac{5sqrt[4]{7sqrt[3]{54}+15sqrt[3]{128}}}{3sqrt[3]{4sqrt[4]{32}}+3sqrt[3]{9sqrt[4]{162}}} LaTeX formula: frac{5sqrt[4]{7sqrt[3]{54}+15sqrt[3]{128}}}{3sqrt[3]{4sqrt[4]{32}}+3sqrt[3]{9sqrt[4]{162}}}](https://helpy.quali.me/uploads/formulas/24b4a6305fc3ea3ee004027fc4c73d792ec61f1a.1.1.png)
Решение. На основании формул 1.17 и 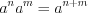
1) ![=5sqrt[4]{2^{frac{1}{3}}cdot 3^4}=5cdot 2^{frac{1}{12}}cdot 3=15cdot 2^{frac{1}{12}} LaTeX formula: =5sqrt[4]{2^{frac{1}{3}}cdot 3^4}=5cdot 2^{frac{1}{12}}cdot 3=15cdot 2^{frac{1}{12}}](http://helpy.quali.me/uploads/formulas/2e0c30c95d9a081fcb42922ed1ecdae29fb5fc10.1.1.png)
2) 
Запишем: 
Ответ: 
1. Среднее арифметическое можно находить как положительных, так и неположительных чисел. Среднее геометрическое чисел находят только в случае, если оба числа положительные.
2. Среднее арифметическое двух положительных чисел 


3. Корни четной степени можно извлекать только из неотрицательных чисел, а нечетной степени – и из отрицательных чисел.
4. Корень 
![sqrt[n]{0}=0 LaTeX formula: sqrt[n]{0}=0](http://helpy.quali.me/uploads/formulas/2e9bcf79de39c3a235d17377ecf0e17ebe118be7.1.1.png)

Найдите среднее арифметическое корней уравнения

Комментарии

ankakundas<br />Ankakundas<br />хорошист<br />ОТВЕТЫ<br /> <br />БАЛЛЫ<br /> <br />БЛАГОДАРНОСТИ<br /> <br />Ответы по<br /> <br /> <br />очень срочно, помогите пожалуйста

очень срочно, помогите пожалуйста

Светило науки — 538 ответов — 0 раз оказано помощи
Среднее арифметическое корней -это сумма корней деленная на их количество, поскольку корень всего 1. то среднее арифметическое будет равно самому корню, то есть среднее арифметическое будет равно 14
Ответ:14


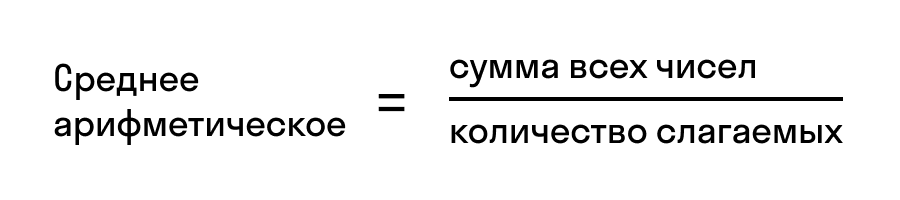

























































































![frac{sqrt[4]{3}}{sqrt[4]{48}}-left ( -1 cdot left | -2 right | right )^2=sqrt[4]{frac{3}{48}}- (-2)^2=sqrt[4]{frac{1}{16}}-4=0,5-4= LaTeX formula: frac{sqrt[4]{3}}{sqrt[4]{48}}-left ( -1 cdot left | -2 right | right )^2=sqrt[4]{frac{3}{48}}- (-2)^2=sqrt[4]{frac{1}{16}}-4=0,5-4=](https://helpy.quali.me/uploads/formulas/e5f0fcb05950d1e40a92115320494f596ef3c8de.1.1.png)
![5sqrt[4]{7sqrt[3]{2cdot 3^3}+15sqrt[3]{2^7}}=5sqrt[4]{7cdot 2^{frac{1}{3}}cdot 3+15cdot 2^{frac{7}{3}}}=5sqrt[4]{2^{frac{1}{3}}(21+15cdot 4)} LaTeX formula: 5sqrt[4]{7sqrt[3]{2cdot 3^3}+15sqrt[3]{2^7}}=5sqrt[4]{7cdot 2^{frac{1}{3}}cdot 3+15cdot 2^{frac{7}{3}}}=5sqrt[4]{2^{frac{1}{3}}(21+15cdot 4)}](http://helpy.quali.me/uploads/formulas/a4d9a537171a662f2085e2e9381f038d821b7d7a.1.1.png)
![3sqrt[3]{2^2 cdot sqrt[4]{2^5}}+3sqrt[3]{3^2 cdot sqrt[4]{2cdot 3^4}}=3cdot 2^{frac{2}{3}}cdot 2^{frac{5}{12}}+3cdot 3 ^{frac{2}{3}}cdot 2^{frac{1}{12}}cdot 3^{frac{1}{3}} LaTeX formula: 3sqrt[3]{2^2 cdot sqrt[4]{2^5}}+3sqrt[3]{3^2 cdot sqrt[4]{2cdot 3^4}}=3cdot 2^{frac{2}{3}}cdot 2^{frac{5}{12}}+3cdot 3 ^{frac{2}{3}}cdot 2^{frac{1}{12}}cdot 3^{frac{1}{3}}](https://helpy.quali.me/uploads/formulas/ff56c5250b69a55f5088a02bacc28aad65455d36.1.1.png)