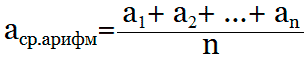Как найти среднее арифметическое чисел с неизвестным

Среднее арифметическое — это число, равное сумме всех чисел множества, делённой на их количество.

Среднее арифметическое двух чисел вычисляется по формуле:

X_ср — среднее арифметическое 2-х чисел;
X₁ — первое число;
X₂ — второе число.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета среднего арифметического двух чисел (среднее между двумя числами). С помощью этого калькулятора вы в один клик сможете рассчитать среднее арифметическое 2-х чисел, если известны исходные числа.

Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.

Смысл коэффициента

Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:

Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.

Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.

Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.

Рассмотрим пару примеров

Расчет средней оценки

Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:

(3 + 3 + 5 + 4) / 4 = 3,75

Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.

Расчет съеденных конфет

Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.

Заключение

Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.

Что такое среднее арифметическое

Средним арифметическим нескольких величин является отношение суммы этих величин к их количеству.

Среднее арифметическое определенного ряда чисел называется сумма всех этих чисел, поделенная на количество слагаемых. Таким образом, среднее арифметическое является средним значением числового ряда.

Чему равно среднее арифметическое нескольких чисел? А равно они сумме этих чисел, которая поделена на количество слагаемых в этой сумме.

Как найти среднее арифметическое число

В вычислении или нахождении среднего арифметического нескольких чисел, нет ничего сложного, достаточно сложить все представленные числа, а полученную сумму разделить на количество слагаемых. Полученный результат и будет средним арифметическим этих чисел.

Рассмотрим этот процесс более подробно. Что же нам нужно сделать для вычисления среднего арифметического и получения конечного результата этого числа.

Во-первых, для его вычисления нужно определить набор чисел или их количество. В этот набор могут входить большие и маленькие числа, и их количество может быть каким угодно.

Во-вторых, все эти числа нужно сложить и получить их сумму. Естественно, если числа несложные и их небольшое количество, то вычисления можно произвести, записав от руки. А если же набор чисел впечатляющий, то лучше воспользоваться калькулятором или электронной таблицей.

И, в-четвертых, полученную от сложения сумму необходимо разделить на количество чисел. В итоге мы получим результат, который и будет средним арифметическим числом этого ряда.

Для чего нужно среднее арифметическое

Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.

Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.

Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.

Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.

Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,

15 + 20 + 25 + 25 + 30 = 115

Теперь разделим эту сумму на количество дней

Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.

Домашнее задание

1.Путем нехитрых вычислений найдите среднее арифметическое число посещаемости учеников вашего класса за неделю.

2. Найдите среднее арифметическое:

3. Решите задачу:

Тема среднего арифметического и среднего геометрического входит в программу математики 6-7 классов. Так как параграф довольно прост для понимания, его быстро проходят, и к завершению учебного года школьники его забывают. Но знания в базовой статистике нужны для сдачи ЕГЭ, а также для международных экзаменов SAT. Да и для повседневной жизни развитое аналитическое мышление никогда не помешает.

Как вычислить среднее арифметическое и среднее геометрическое чисел

Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?

Решение: (11 + 4 + 3) / 3 = 6

В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.

Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.

Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:

Решение: ∛(4 × 2 × = 4

В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое — ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.

Может ли так произойти, что среднее арифметическое станет равным среднему геометрическому?

Конечно, может. Но только в двух случаях. Если имеется ряд чисел, состоящий только либо из единиц, либо из нулей. Примечательно также то, что ответ не зависит от их количества.

Доказательство с единицами: (1 + 1 + 1) / 3 = 3 / 3 = 1 (среднее арифметическое).

∛(1 × 1 × 1) = ∛1 = 1(среднее геометрическое).

Доказательство с нулями: (0 + 0) / 2=0 (среднее арифметическое).

√(0 × 0) = 0 (среднее геометрическое).

Другого варианта нет и быть не может.

Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.

Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.

В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.

Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:

1. Первоначально требуется провести операцию сложения выбранных чисел. Это часто можно сделать, как говорится, вручную, не используя электронную технику.
2. После того как сложение произведено и получен его результат необходимо произвести деление. Данная операция подразумевает разделение суммы двух сложенных чисел на два – количество сложенных чисел. Именно такое действие и позволит получить требуемую величину.

Формула

Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:

В этой формуле применяется следующее обозначение:

А и В – это заранее выбранные числа, для которых необходимо находить значение.

Нахождение значения для трёх

Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:

1. Для этого следует выбрать числа, необходимые в расчёте, и сложить их для получения общей суммы.
2. После того как данная сумма трёх будет найдена, требуется опять совершить процедуру деления. При этом полученную сумму надо разделить уже на три, что соответствует количеству выбранных чисел.

Формула

Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:

В данной формуле принято следующее обозначение:

А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Подсчёт среднего арифметического пяти

Выполнение данной операции потребует проведения определённого алгоритма действий.

1. Прежде всего, надо выбрать пять чисел, для которых будет проходить вычисление среднего арифметического. После данного подбора эти числа, как и в предыдущих вариантах, необходимо просто сложить и получить конечную сумму.
2. Полученную сумму надо будет поделить по их количеству на пять, что и позволит получить требуемое значение.

Формула

Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:

В данной формуле переменные имеют такое обозначение:

А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.

Универсальная формула вычисления

Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического , можно обратить внимание на то, что у них есть общая закономерность.

Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.

Главным при определении формулы является принцип расчёта среднего арифметическог о.

Данный принцип как было видно из приведённых примеров, выглядит таким образом:

1. Производится подсчёт количества чисел, которые заданы для получения требуемого значения. Эта операция может быть проведена как вручную при небольшом количестве чисел, так и при помощи вычислительной техники.
2. Проводится суммирование выбранных чисел. Эта операция в большинстве ситуаций выполняется при помощи вычислительной техники, так как числа могут состоять из двух, трёх и более цифр.
3. Сумма, которая получена в результате сложения выбранных чисел, должна быть поделена на их количество. Данная величина определяется на первоначальном этапе расчёта среднего арифметического.

Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:

Данная формула содержит следующие переменные:

А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.

N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.

Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.

Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.

В математике среднее арифметическое значение чисел (или просто среднее) — это сумма всех чисел в данном наборе, разделенная на их количество. Это наиболее обобщенное и распространенное понятие средней величины. Как вы уже поняли, чтобы найти нужно суммировать все данные вам числа, а полученный результат разделить на количество слагаемых.

Что такое среднее арифметическое?

Давайте рассмотрим пример.

Пример 1 . Даны числа: 6, 7, 11. Нужно найти их среднее значение.

Для начала найдем сумму всех данных чисел.

Теперь разделим получившуюся сумму на количество слагаемых. Так как у нас слагаемых три, соответственно, мы будем делить на три.

Следовательно, среднее значение чисел 6, 7 и 11 — это 8. Почему именно 8? Да потому, что сумма 6, 7 и 11 будет такая же, как трех восьмерок. Это отлично видно на иллюстрации.

Среднее значение чем-то напоминает «выравнивание» ряда чисел. Как видите, кучки карандашей стали одного уровня.

Рассмотрим еще один пример, чтобы закрепить полученные знания.

Пример 2. Даны числа: 3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29. Нужно найти их среднее арифметическое значение.

3 + 7 + 5 + 13 + 20 + 23 + 39 + 23 + 40 + 23 + 14 + 12 + 56 + 23 + 29 = 330

Делим на количество слагаемых (в этом случае — 15).

Следовательно, среднее значение данного ряда чисел равно 22.

Теперь рассмотрим отрицательные числа. Вспомним, как их суммировать. Например, у вас есть два числа 1 и -4. Найдем их сумму.

Зная это, рассмотрим еще один пример.

Пример 3. Найти среднее значение ряда чисел: 3, -7, 5, 13, -2.

Находим сумму чисел.

3 + (-7) + 5 + 13 + (-2) = 12

Так как слагаемых 5, разделим получившуюся сумму на 5.

Следовательно, среднее арифметическое значение чисел 3, -7, 5, 13, -2 равно 2,4.

В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, значение с помощью этой программы.

Для того чтобы посчитать среднее значение ряда чисел, необходимо использовать функцию AVERAGE. Синтаксис для этой функции:
= Average (argument1, argument2, . argument255)
где argument1, argument2, . argument255 — это либо числа, либо ссылки на ячейки (под ячейками подразумеваются диапазоны и массивы).

Чтобы было более понятно, опробуем полученные знания.

1. Введите числа 11, 12, 13, 14, 15, 16 в ячейки С1 — С6.
2. Выделите ячейку С7, нажав на нее. В этой ячейке у нас будет отображаться среднее значение.
3. Щелкните на вкладке «Формулы».
4. Выберите More Functions > Statistical для того, чтобы открыть
5. Выберите AVERAGE. После этого должно открыться диалоговое окно.
6. Выделите и перетащите туда ячейки С1-С6, чтобы задать диапазон в диалоговом окне.
7. Подтвердите свои действия клавишей «ОК».
8. Если вы все сделали правильно, в ячейке С7 у вас должен появиться ответ — 13,7. При нажатии на ячейку C7 функция (= Average (C1: C6)) будет отображаться в строке формул.

Очень удобно использовать эту функцию для ведения учета, накладных или когда вам просто нужно найти среднее значение из очень длинного ряда чисел. Поэтому ее часто используют в офисах и крупных компаниях. Это позволяет сохранять порядок в записях и дает возможность быстро посчитать что-либо (например, средний доход за месяц). Также с помощью Excel можно найти среднее значение функции.

Ответ: каждому досталось по 4 груши.

Пример 2. На курсы английского языка в понедельник пришло 15 человек, во вторник — 10, в среду — 12, в четверг — 11, в пятницу — 7, в субботу — 14, в воскресенье — 8. Найти среднюю посещаемость курсов за неделю.
Решение: Найдем среднее арифметическое:

Ответ: в среднем на курсы английского языка приходило 11 человек в день.

Пример 3. Гонщик ехала два часа со скоростью 120 км/ч и час со скоростью 90 км/ч. Найдите среднюю скорость автомобиля во время гонки.
Решение: Найдем среднее арифметическое скоростей автомобиля за каждый час пути:

Ответ: средняя скорость автомобиля во время гонки была 110 км/ч.

Пример 4. Среднее арифметическое 3 чисел равно 6, а среднее арифметическое 7 других чисел равно 3. Чему равно среднее арифметическое этих десяти чисел?
Решение: Так как среднее арифметическое 3-х чисел равно 6 то их сумма равна 6 · 3 = 18, аналогично сумма оставшихся 7-ми чисел равна 7 · 3 = 21.
Значит сумма всех 10-ти чисел будет 18 + 21 = 39, а среднее арифметическое равно

Среднее арифметическое

Составитель: 
учитель математики МОУ СОШ №26

г.
Ярославля

Мизулина
Т.Н.

2015-2016

Тема
«Среднее арифметическое»   5-6 класс

Результаты:

1. Оперировать понятием среднее арифметическое
   двух и нескольких чисел.
2. Изображать среднее арифметическое на
   координатной прямой.
3. Решать задачи на нахождение среднего
   арифметического двух и нескольких чисел.
4. Находить сумму чисел по среднему
   арифметическому.
5. Читать и извлекать информацию,
   представленную в таблицах и диаграммах.
6. Решать задачи практической направленности и
   уметь интерпретировать полученный результат.
7. Познакомиться со свойствами среднего
   арифметического.

Подбор задач, соответствующих теме «Среднее арифметическое»

1. В таблице показан расход электроэнергии
   некоторой семьёй в течение года:

Найдите
средний ежемесячный расход
электроэнергии этой семьёй.

Решение:

(85+80+74+61+54+34+32+32+62+78+81+83):12=63

Ответ:
среднемесячный расход электроэнергии составляет 63 КВт-ч.

1. На соревнованиях по фигурному катанию судьи
   поставили спортсмену следующие оценки:

5,2   5,4   5,5  
5,4   5,1    5,4    5,5    5,3.

Для полученного
ряда найдите среднее арифметическое. Что характеризует это показание?

Решение:

Заметим, что сумму
этих чисел можно посчитать следующим способом

(5,1+5,2+5,3+5,4*3+5,5*2):8=5,32

Ответ: 5,32 – это
средний балл за выступление спортсмена.

1. Все числа равны между собой. Чему равно их
   среднее арифметическое?

Решение: 

1)Проверить на
примере двух, нескольких чисел.

2)Доказать
утверждение в общем виде.

Пусть неизвестные
числа будут   х, тогда их сумма запишется как     х*n, где
n-это количество чисел, по определению среднего
арифметического получим   (х *n):n=х

Ответ: среднее
арифметическое совпадает с указанным числом в ряду.

1. Пусть а – некоторое число. Вычислите среднее
   арифметическое набора чисел:

а) х  б) х

5. Придумайте
четыре таких числа, что их среднее арифметическое равно:

а)второму по
величине числу;

б)третьему по величине
числу;

в)Полусумме второго
и третьего по величине этих чисел.

Решение:

а) Учащиеся могут
подобрать данный ряд чисел. Но можно предложить и решение в общем виде,
например: обозначим числа a,b,c,d. По условию (a+b+c+d):4=b, тогда a+b+c+d=4b;   a+c+d=3b,
например пусть a=5, c=7,d=9, тогда b=21:3=7.

Ответ : задача
имеет много решений.

б) Аналогично а)

в) Учащиеся также
могут попробовать подобрать ряд чисел, удовлетворяющих условию, таких вариантов
окажется несколько, поэтому можно рассуждать подобным образом как в 
упражнении    а)  придём к выводу, что b+c=a+d.

6. Придумайте 5
таких чисел, что их среднее арифметическое

а) больше четырёх
из них;

б) меньше четырёх
из них.

Решение:

а) 4*a >

теперь можно
подобрать такие числа, например: 1, 2, 3, 4 и 79 и их среднее арифметическое
17,8;

б) аналогично 4*a
<, например 19,15, 17, 20 и  -1 их
среднее арифметическое  14.

1. Отметьте числа, полученные в предыдущей
   задаче на координатной прямой. Укажите положение их среднего
   арифметического. Какую особенность вы заметили?

Указание:

в  задаче речь идёт
о центре равновесия,  положение  которого соответствует   среднему 
арифметическому  ряда чисел,  а также на координатной прямой видна удалённость
чисел от значения среднего арифметического.

Например: 1, 2, 3,
4, 79 и их среднее арифметическое  17, 8

1. Можете ли вы без вычислений указать среднее
   значение набора чисел. Проверьте свои предположения вычислениями:

а) 13, 14, 15,
16,17;

б)16, 17, 18, 19,
20;

в)21, 22, 23, 24,
25;

г)20, 25, 30, 35,
40;

д)22, 24, 26, 28, 30;

е)102, 104, 106,
108, 110.

Ответ: в каждом
случае среднее арифметическое совпадает с третьим числом из ряда.

9. Отметьте числа и
их среднее арифметическое на  числовой прямой:

а) 1, 2, 3, 4;

б) 2, 3, 4, 5;

в) 10, 11, 12, 13.

Какую
закономерность в поведении среднего значения можно заметить в каждом из
случаев?

Ответ: в каждом
случае среднее арифметическое совпадает с полусуммой двух средних чисел.

1. Вычислите средние арифметические наборов
   чисел:

а)2, 4, 7, 8, 9;

б) 20, 40, 70, 80,
90;

в) 200, 400, 700,
800, 900.

Какую
закономерность можно наблюдать в поведении средних значений?

Ответ: в задаче
используется свойство: среднее арифметическое ряда чисел ахравно произведению числа а на среднее
арифметическое ряда х

1. Вычислите среднее арифметическое наборов
   чисел:

а) 10, 20, 35, 40,
45;

б) 13, 23, 38, 43,
48;

г) 7, 13, 28, 33,
38.

Какую
закономерность можно наблюдать в поведении средних значений?

Ответ:  в задаче
используется свойство: среднее арифметическое ряда чисел а+хравно сумме числа а и среднего
арифметического  ряда х

1. При изучении качества продукции, выпущенной
   цехом, определяли число бракованных деталей в каждом из 50 произвольным
   образом выбранных ящиков с одинаковым числом деталей. Получили такую
   таблицу:

Найдите среднее
арифметическое полученного ряда данных. Объясните практический смысл этой
статистической характеристики.

Решение:

(0*8+1*22+2*13+3*5+4*2):50=1,42

Ответ: по 1,42 
бракованной детали было бы в каждом ящике, если бы распределяли детали
равномерно, причём 1,42*50=71 – общее число бракованных деталей во всей партии.

1. В ряду данных, состоящем из 12 чисел,
   наибольшее число увеличили на 6. Изменится ли среднее арифметическое этого
   ряда?

Решение:

Пусть среднее
арифметическое чисел первоначального ряда было х, тогда 12*х – это сумма всех
чисел, получим  (12*х+6):12=х+0,5

Ответ: среднее
арифметическое увеличится на 0,5.

1. В ряду данных, состоящем из 15 чисел,
   наименьшее число уменьшили на 5. Изменится ли среднее арифметическое?

Решение:

(15*х-5):15=х-1/3

Ответ: среднее
арифметическое уменьшится на 1/3.

1. После урока по теме «Статистика» на доске
   осталась таблица:

и ответ: «Ср. арифм.=10».

а) Заполните пустое
место в таблице

б) Может ли в
ответе для среднего арифметического стоять 15?

Решение:

а)  

арифметически:               
10*10=100

                                            
100-20-14=66

                                             
66:3=22

с помощью уравнения:      
обозначим отсутствующее число  х, тогда                  (4*5+7*2+х*3):10=10

          х=22

б) Если среднее
арифметическое будет 15, то

(4*5+7*2+х*3):10=15                     
или           (15*10-20-14):3= 38 

х= 38 не удовлетворяет условию задачи.

Ответ: А)
пропущенное число 22,

             Б) не
может.

1. Проведя учёт бракованных деталей в
   контрольной партии ящиков, составили таблицу, в которой два числа
   оказались стёртыми:

Восстановите их, зная, что ящиков с двумя
бракованными деталями оказалось вдвое больше, чем ящиков с тремя бракованными
деталями, а в среднем в каждом ящике было по 1, 85 бракованных деталей.

Решение:

Пусть ящиков с тремя бракованными деталями
было х, тогда по условию задачи получим    (0*12+1*28+2*2х+3*х+4*7+5*2):(3х+49)=1,85

                          
х=17.

 2*17=34

Ответ: 34 и 17.

1. У группы из 20 учащихся спросили, сколько
   примерно часов в день они тратят на приготовление домашних заданий. Ответы
   представлены на диаграмме, изображённой на рисунке. Сколько времени в день
   в среднем тратит ученик из этой группы на приготовление домашних заданий?

Ответ: 2,4

1. Предприниматель Семён открыл мужскую
   парикмахерскую «Куафер Симон». Семён предлагает следующий прейскурант цен:

А – « Под
нуль»      40 р.

Б –
«Полубокс          50 р.

В –
Канадка              60 р.

Г – «Звезда
рока»     180 р.

Д – « Мамин сын» 
400р.

Будучи человеком
рачительным, Семён ведёт строгий учёт дохода, для чего он завёл специальную
книжку. Вот записи по месяцам за первые полгода:

1)     
Каково среднее количество стрижек в рабочий день?
(В месяце 20 рабочих дней).

2)     
Какой  средний доход от одной стрижки?

3)     
Чему равен среднемесячный доход Семёна?

4)     
Каков чистый среднемесячный заработок Семёна, если
он платит налог в размере 13% от дохода и ежемесячную арендную плату 2000
рублей в месяц?

Решение:

1)     
(165+159+192+163+175+216):120 8,9

2)     
(226*40+316*50+339*60+154*180+35*400):107081,2

3)     
(226*40+316*50+339*60+154*180+35*400): 614483,33

4)     
(86900 – ((226*40+316*50+339*60+154*180+35*400)*
0,13+6*2000)) :6= 10600,5

Ответ:
1) 8,9;

           
2) 81,2 руб.;

           
3) 14483,33 руб.;

           
4) 10600,5 руб.