Загрузить PDF
Загрузить PDF
В любом тесте, проводимом на заданной группе населения, важно подсчитать чувствительность[1]
, специфичность[2]
, положительную прогностическую значимость[3]
и отрицательную прогностическую значимость[4]
для того, чтобы определить, насколько полезен этот тест в диагностике заболевания или особенностей данной группы населения. Если мы хотим использовать этот тест для исследования характерных особенностей у отобранной группы населения, нам необходимо знать:
- С какой вероятностью тест выявит наличие признаков у человека с характерными признаками (чувствительность)?
- С какой вероятностью тест выявит отсутствие признаков у человека без характерных признаков (специфичность)?
- С какой вероятностью у человека с положительным результатом теста на самом деле есть признаки (положительная прогностическая значимость)?
- С какой вероятностью у человека с отрицательным результатом теста на самом деле нет признаков (отрицательная прогностическая значимость)?
Очень важно подсчитать эти значения для того, чтобы определить, полезен ли тест в оценке характерных особенностей заданной группы населения. В этой статье мы покажем, как подсчитать эти значения.
-
1
Постройте выборочную совокупность населения, например, 1000 пациентов в клинике.
-
2
Определите заболевание или признаки, являющиеся объектом исследования, к примеру, сифилис.
-
3
Проведите надежный тест, соответствующий золотому стандарту для того, чтобы определить уровень распространения заболевания или признаков, к примеру, информация о наличии бактерии бледной трепонемы, полученная с помощью темнопольного микроскопа, с учетом клинической картины. Используйте тест, соответствующий золотому стандарту для того, чтобы определить, у кого есть признаки, а у кого нет. Для наглядности предположим, что у 100 испытуемых они есть, а у 900 нет.
-
4
Составьте тест по интересующим вас чувствительности, специфичности, положительной прогностической значимости и отрицательной прогностической значимости населения и протестируйте выборочную совокупность населения. Например, пусть это будет быстрый плазма реагент (RPR) тест на сифилис. Используйте его для выборочного тестирования 1000 человек.
-
5
Из тех, у кого есть признаки (как установлено золотым стандартом), выпишите количество людей с положительными и отрицательными результатами. Таким же образом протестируйте людей, у которых нет признаков (как установлено золотым стандартом). Вы получите четыре цифры. Люди с признаками И положительным результатом являются истинно положительными (ИП). Люди с признаками И отрицательным результатом являются ложноотрицательными (ЛО). Люди без признаков И с положительным результатом являются ложноположительными (ЛП). Люди без признаков И с отрицательным результатом являются истинно отрицательными (ИО). Для наглядности предположим, что вы протестировали на RPR 1000 пациентов. У 95 из 100 пациентов, больных сифилисом, был положительный результат, а у 5 – отрицательный. Из 900 пациентов, не больных сифилисом, у 90 был положительный результат, а у 810 – отрицательный. В этом случае ИП=95, ЛО=5, ЛП=90 и ИО=810.
-
6
Чтобы подсчитать чувствительность, разделите ИП на (ИП+ЛО). В вышеупомянутом случае у нас получится 95/(95+5)= 95%. Чувствительность показывает нам, с какой вероятностью тест покажет положительный результат у человека, имеющего признаки. Среди людей, имеющих признаки, какая доля получит положительный результат? Чувствительность, равная 95% — довольно неплохо.
-
7
Чтобы подсчитать специфичность, разделите ИО на (ЛП+ИО). В вышеупомянутом случае у нас получится 810/(90+810)= 90%. Специфичность показывает нам, с какой вероятностью тест покажет отрицательный результат у человека, не имеющего признаков. Среди людей, не имеющих признаков, какая доля получит отрицательный результат? Специфичность, равная 90% — довольно неплохо.
-
8
Чтобы подсчитать положительную прогностическую значимость (ППЗ), разделите ИП на (ИП+ЛП). В вышеупомянутом случае у нас получится 95/(95+90)= 51.4%. Положительная прогностическая значимость показывает нам, с какой вероятностью человек с положительным результатом будет иметь признаки. Среди людей, имеющих положительный результат, какая доля действительно имеет признаки? ППЗ, равная 51.4%, означает, что если у вас положительный результат, вероятность того, что вы на самом деле больны, равна 51.4%.
-
9
Чтобы подсчитать отрицательную прогностическую значимость (ОПЗ), разделите ИО на (ИО+ЛО). В вышеупомянутом случае у нас получится 810/(810+5)= 99.4%. Отрицательная прогностическая значимость показывает нам, с какой вероятностью человек с отрицательным результатом теста не будет иметь признаков. Среди людей, имеющих отрицательный результат, какая доля действительно не имеет признаков? ОПЗ, равная 99.4%, означает, что если у вас отрицательный результат, вероятность того, что вы не больны, равна 99.4%.
Реклама
Советы
- Хорошие скрининг-тесты имеют высокую чувствительность и помогают выявить больных, у которых есть признаки. Тесты с высокой чувствительностью полезны в дифференциальной диагностике заболеваний или признаков, если они показывают отрицательный результат. («SNOUT»: отклонение чувствительности)
- Точность или эффективность – это процентное соотношение результатов теста, точно установленных тестом, то есть (истинно положительные + истинно отрицательные)/общие результаты теста = (ИП+ИО)/(ИП+ИО+ЛП+ЛО).
- Попробуйте начертить таблицу сопряженности для того, чтобы облегчить себе задачу.
- Помните, что чувствительность и специфичность – это внутренние свойства данного теста, которые не зависят от заданной группы населения, то есть если тест проводиться на разных группах населения, эти две величины должны оставаться без изменений.
- Хорошие контрольные тесты имеют высокую специфичность, таким образом, при тестировании не будет допущено ошибок в выявлении пациентов, имеющих признаки. Тесты с высокой чувствительностью полезны в диагностике заболеваний или признаков, если они показывают положительный результат. («SPIN»: одобрение специфичности)
- С другой стороны, положительная прогностическая значимость и отрицательная прогностическая значимость зависят от уровня распространения признаков среди отобранной группы населения. Чем реже встречаются признаки, тем ниже положительная прогностическая значимость и выше отрицательная прогностическая значимость (так как распространенность ниже в случаях, когда признаки встречаются реже). И наоборот, чем чаще встречаются признаки, тем выше положительная прогностическая значимость и ниже отрицательная прогностическая значимость (так как распространенность выше в случаях, когда признаки встречаются чаще).
- Постарайтесь хорошо понять эти определения.
Реклама
Предупреждения
- Легко допустить ошибки в расчетах по невнимательности. Тщательно проверяйте свои подсчеты. В этом вам поможет таблица сопряженности.
Реклама
Источники
Об этой статье
Эту страницу просматривали 15 516 раз.
Была ли эта статья полезной?
Оценка чувствительности и специфичности диагностических тестов
Еще одна сфера
применения таблицы сопряженности —
сравнение двух диагностических тестов.
На их основе можно оценить специфичность
и чувствительность нового метода.
Чувствительность
(Se)
—
это доля действительно болеющих людей
в обследованной популяции,
которые по результатам теста выявляются
как больные. Чувствительность — это мера
вероятности того, что любой случай
болезни (состояния) будет идентифицирован
с помощью теста. В клинике тест с высокой
чувствительностью полезен для исключения
диагноза, если результат отрицателен.
Специфичность
(Sp)
—
это доля тех, у которых тест отрицателен,
среди всех людей, не имеющих болезни
(состояния). Это мера вероятности
правильной идентификации людей, не
имеющих болезни, с помощью теста. В
клинике тест с высокой специфичностью
полезен для включения диагноза в число
возможных в случае положительного
результата.
Чувствительность
и специфичность нового метода определяется
относительно другого, общепринятого,
который обладает высокой точностью, но
имеет другие недостатки – побочные
эффекты, дороговизну, недоступность и
т.д. Этот другой метод называют «золотым
стандартом».
Таблица 45. Оценка
нового диагностического теста
|
Результат |
Результаты |
|
|
положительный |
отрицательный |
|
|
положительный |
ИП число |
ЛП число |
|
отрицательный |
ЛО число |
ИО число |
Чувствительность

Специфичность

Специфичность
и чувствительность теста являются
выборочными характеристиками, не
являются абсолютными и неизменными и
зависят от объема выборки. Поэтому
полезно определять стандартную ошибку
и доверительный интервал для этих
величин.
Оценка прогностического значения диагностических тестов
Аналогичные
таблицы возникают и при
оценке прогностического значения теста.
Предположим нам необходимо оценить
способность некоторого теста прогнозировать
заболевание.
После
этого определим на основании этого
показателя:
число
истинно-положительных прогнозов (ИП) —
число больных, у которых согласно
значению данного теста могло быть
предсказано заболевание и которые
действительно болеют;
число
ложноположительных (ЛП) прогнозов
(согласно значению данного показателя
предсказывается болезнь, но пациент
оказался здоров);
число
ложноотрицательных (ЛО) прогнозов
(согласно значению данного показателя
предсказывается, что пациент здоров,
но на самом деле он болеет);
число
истинно отрицательных (ИО) прогнозов
(больной должен был быть здоровым и он
действительно здоров).
Таблица 46.
Прогностическая способность теста
|
Прогноз |
Исход |
|
|
неблагоприятный |
благоприятный |
|
|
неблагоприятный |
ИП число |
ЛП число |
|
благоприятный |
ЛО число |
ИО число |
Для
прогностического тетста можно определить
чувствительность и специфичность, а
также распространенность
(prevalence), которая определяется как
отношение числа лиц с наличием заболевания
(или любого другого состояния) ко всей
исследуемой популяции:

Прогностическая
ценность положительного результата
(positive predictive value) — вероятность наличия
заболевания при положительном
(патологическом) результате теста:

Отношение
правдоподобия (likelihood
ratio)
для
положительного результата
показывает во сколько раз вероятность
положительного результата теста у
больных больше, чем у здоровых

Отношение
правдоподобия для отрицательного
результата
показывает во сколько раз вероятность
отрицательного теста у больных больше,
чем у здоровых
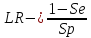
Диагностическая
эффективность
теста выражается процентным отношением
истинных (и положительных, и отрицательных)
результатов теста к общему числу
полученных результатов.

|
Пример.
Таблица 47. Данные Клинический всего присутствует о сутствует ß-гемолитический да ИП(a) 27 ЛП(b) 35 62 нет ЛО(c) 10 ИО(d) 77 87 всего 37 112 149
т.е.
т.е.
т.е.
т.е.
т.е.
т.е.
т.е. |
Контрольное
задание 10:
В
таблице приведены данные о частоте
встречаемости лиц с избытком веса среди
лиц с нормальным и повышенным АД. По
данным из таблицы ответьте на поставленные
вопросы
|
АД |
АД |
|
|
выраж. |
88 |
120 |
|
выраж. |
363 |
1668 |
-
Во
сколько раз чаще повышенное САД
встречается у лиц с выраженным ожирением -
Во
сколько раз увеличивается риск
артериальной гипертонии у лиц, имеющих
избыток веса
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение
В статистике чувствительность теста соответствует его способности давать положительный результат при проверке гипотезы.
другой стороны, специфичность измеряет способность теста давать отрицательный результат, когда гипотеза не подтверждается.
Эти две концепции необходимы для измерения качества проводимого теста, особенно в эпидемиологии.
Оценка теста
Чтобы оценить эти два параметра, необходимо протестировать проверенные случаи и провести тестирование на них. Результаты делятся на четыре категории:
Цель состоит в том, чтобы достичь максимального количества истинно положительных и истинно отрицательных результатов и наименьшего количества ложных положительных и ложных отрицательных результатов. В медицине особенно важно минимизировать количество ложноотрицательных случаев, которые могут иметь серьезные последствия. Однако поиск ложных срабатываний может привести к большему количеству ложных срабатываний.
Результаты можно представить в виде следующей таблицы:
Таким образом, с помощью этой таблицы мы можем измерить специфичность и чувствительность теста.
Чувствительность — это вероятность получения положительного результата при болезни:
Специфичность соответствует вероятности получения отрицательного результата при отсутствии болезни:
Таким образом, в медицине или эпидемиологии обычно цель состоит в том, чтобы иметь высокую чувствительность.
Пример
Если вы пройдете тест, который выявляет болезнь A. Тестируется 1000 пациентов, 500 больных и 500 здоровых.
Мы проводим тест и получаем следующие результаты:
Таким образом, мы можем рассчитать чувствительность и специфичность:
Sensitivity and specificity — The left half of the image with the solid dots represents individuals who have the condition, while the right half of the image with the hollow dots represents individuals who do not have the condition. The circle represents all individuals who tested positive.
Sensitivity and specificity mathematically describe the accuracy of a test which reports the presence or absence of a condition. If individuals who have the condition are considered «positive» and those who don’t are considered «negative», then sensitivity is a measure of how well a test can identify true positives and specificity is a measure of how well a test can identify true negatives:
- Sensitivity (true positive rate) is the probability of a positive test result, conditioned on the individual truly being positive.
- Specificity (true negative rate) is the probability of a negative test result, conditioned on the individual truly being negative.
If the true status of the condition cannot be known, sensitivity and specificity can be defined relative to a «gold standard test» which is assumed correct. For all testing, both diagnostic and screening, there is usually a trade-off between sensitivity and specificity, such that higher sensitivities will mean lower specificities and vice versa.
A test which reliably detects the presence of a condition, resulting in a high number of true positives and low number of false negatives, will have a high sensitivity. This is especially important when the consequence of failing to treat the condition is serious and/or the treatment is very effective and has minimal side effects.
A test which reliably excludes individuals who do not have the condition, resulting in a high number of true negatives and low number of false positives, will have a high specificity. This is especially important when people who are identified as having a condition may be subjected to more testing, expense, stigma, anxiety, etc.
Sensitivity and specificity
The terms «sensitivity» and «specificity» were introduced by American biostatistician Jacob Yerushalmy in 1947.[1]
Sources: Fawcett (2006),[2] Piryonesi and El-Diraby (2020),[3] |
There are different definitions within laboratory quality control, wherein «analytical sensitivity» is defined as the smallest amount of substance in a sample that can accurately be measured by an assay (synonymously to detection limit), and «analytical specificity» is defined as the ability of an assay to measure one particular organism or substance, rather than others.[12] However, this article deals with diagnostic sensitivity and specificity as defined at top.
Application to screening study[edit]
Imagine a study evaluating a test that screens people for a disease. Each person taking the test either has or does not have the disease. The test outcome can be positive (classifying the person as having the disease) or negative (classifying the person as not having the disease). The test results for each subject may or may not match the subject’s actual status. In that setting:
- True positive: Sick people correctly identified as sick
- False positive: Healthy people incorrectly identified as sick
- True negative: Healthy people correctly identified as healthy
- False negative: Sick people incorrectly identified as healthy
After getting the numbers of true positives, false positives, true negatives, and false negatives, the sensitivity and specificity for the test can be calculated. If it turns out that the sensitivity is high then any person who has the disease is likely to be classified as positive by the test. On the other hand, if the specificity is high, any person who does not have the disease is likely to be classified as negative by the test. An NIH web site has a discussion of how these ratios are calculated.[13]
Definition[edit]
Sensitivity[edit]
Consider the example of a medical test for diagnosing a condition. Sensitivity (sometimes also named the detection rate in a clinical setting) refers to the test’s ability to correctly detect ill patients out of those who do have the condition.[14] Mathematically, this can be expressed as:
A negative result in a test with high sensitivity can be useful for «ruling out» disease,[14] since it rarely misdiagnoses those who do have the disease. A test with 100% sensitivity will recognize all patients with the disease by testing positive. In this case, a negative test result would definitively rule out the presence of the disease in a patient. However, a positive result in a test with high sensitivity is not necessarily useful for «ruling in» disease. Suppose a ‘bogus’ test kit is designed to always give a positive reading. When used on diseased patients, all patients test positive, giving the test 100% sensitivity. However, sensitivity does not take into account false positives. The bogus test also returns positive on all healthy patients, giving it a false positive rate of 100%, rendering it useless for detecting or «ruling in» the disease.
The calculation of sensitivity does not take into account indeterminate test results.
If a test cannot be repeated, indeterminate samples either should be excluded from the analysis (the number of exclusions should be stated when quoting sensitivity) or can be treated as false negatives (which gives the worst-case value for sensitivity and may therefore underestimate it).
A test with a higher sensitivity has a lower type II error rate.
Specificity[edit]
Consider the example of a medical test for diagnosing a disease. Specificity refers to the test’s ability to correctly reject healthy patients without a condition. Mathematically, this can be written as:
A positive result in a test with high specificity can be useful for «ruling in» disease, since the test rarely gives positive results in healthy patients.[15] A test with 100% specificity will recognize all patients without the disease by testing negative, so a positive test result would definitively rule in the presence of the disease. However, a negative result from a test with high specificity is not necessarily useful for «ruling out» disease. For example, a test that always returns a negative test result will have a specificity of 100% because specificity does not consider false negatives. A test like that would return negative for patients with the disease, making it useless for «ruling out» the disease.
A test with a higher specificity has a lower type I error rate.
Graphical illustration[edit]
-
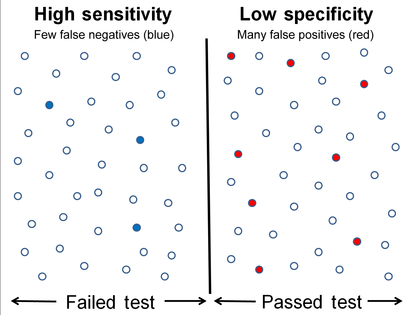
High sensitivity and low specificity
-
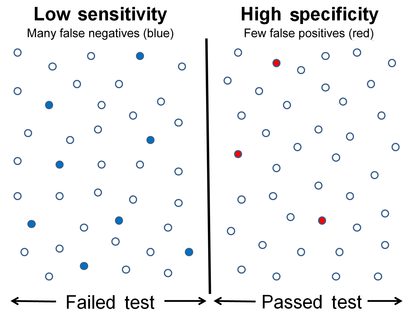
Low sensitivity and high specificity
-
A graphical illustration of sensitivity and specificity
The above graphical illustration is meant to show the relationship between sensitivity and specificity. The black, dotted line in the center of the graph is where the sensitivity and specificity are the same. As one moves to the left of the black dotted line, the sensitivity increases, reaching its maximum value of 100% at line A, and the specificity decreases. The sensitivity at line A is 100% because at that point there are zero false negatives, meaning that all the negative test results are true negatives. When moving to the right, the opposite applies, the specificity increases until it reaches the B line and becomes 100% and the sensitivity decreases. The specificity at line B is 100% because the number of false positives is zero at that line, meaning all the positive test results are true positives.
The middle solid line in both figures that show the level of sensitivity and specificity is the test cutoff point. As previously described, moving this line results in a trade-off between the level of sensitivity and specificity. The left-hand side of this line contains the data points that tests below the cut off point and are considered negative (the blue dots indicate the False Negatives (FN), the white dots True Negatives (TN)). The right-hand side of the line shows the data points that tests above the cut off point and are considered positive (red dots indicate False Positives (FP)). Each side contains 40 data points.
For the figure that shows high sensitivity and low specificity, there are 3 FN and 8 FP. Using the fact that positive results = true positives (TP) + FP, we get TP = positive results — FP, or TP = 40 — 8 = 32. The number of sick people in the data set is equal to TP + FN, or 32 + 3 = 35. The sensitivity is therefor 32 / 35 = 91.4%. Using the same method, we get TN = 40 — 3 = 37, and the number of healthy people 37 + 8 = 45, which results in a specificity of 37 / 45 = 82.2 %.
For the figure that shows low sensitivity and high specificity, there are 8 FN and 3 FP. Using the same method as the previous figure, we get TP = 40 — 3 = 37. The number of sick people is 37 + 8 = 45, which gives a sensitivity of 37 / 45 = 82.2 %. There are 40 — 8 = 32 TN. The specificity therefor comes out to 32 / 35 = 91.4%.
-
A test result with 100 percent sensitivity.
-
A test result with 100 percent specificity.
The red dot indicates the patient with the medical condition. The red background indicates the area where the test predicts the data point to be positive. The true positive in this figure is 6, and false negatives of 0 (because all positive condition is correctly predicted as positive). Therefore, the sensitivity is 100% (from 6 / (6 + 0)). This situation is also illustrated in the previous figure where the dotted line is at position A (the left-hand side is predicted as negative by the model, the right-hand side is predicted as positive by the model). When the dotted line, test cut-off line, is at position A, the test correctly predicts all the population of the true positive class, but it will fail to correctly identify the data point from the true negative class.
Similar to the previously explained figure, the red dot indicates the patient with the medical condition. However, in this case, the green background indicates that the test predicts that all patients are free of the medical condition. The number of data point that is true negative is then 26, and the number of false positives is 0. This result in 100% specificity (from 26 / (26 + 0)). Therefore, sensitivity or specificity alone cannot be used to measure the performance of the test.
Medical usage[edit]
In medical diagnosis, test sensitivity is the ability of a test to correctly identify those with the disease (true positive rate), whereas test specificity is the ability of the test to correctly identify those without the disease (true negative rate).
If 100 patients known to have a disease were tested, and 43 test positive, then the test has 43% sensitivity. If 100 with no disease are tested and 96 return a completely negative result, then the test has 96% specificity. Sensitivity and specificity are prevalence-independent test characteristics, as their values are intrinsic to the test and do not depend on the disease prevalence in the population of interest.[16] Positive and negative predictive values, but not sensitivity or specificity, are values influenced by the prevalence of disease in the population that is being tested. These concepts are illustrated graphically in this applet Bayesian clinical diagnostic model which show the positive and negative predictive values as a function of the prevalence, sensitivity and specificity.
Misconceptions[edit]
It is often claimed that a highly specific test is effective at ruling in a disease when positive, while a highly sensitive test is deemed effective at ruling out a disease when negative.[17][18] This has led to the widely used mnemonics SPPIN and SNNOUT, according to which a highly specific test, when positive, rules in disease (SP-P-IN), and a highly sensitive test, when negative, rules out disease (SN-N-OUT). Both rules of thumb are, however, inferentially misleading, as the diagnostic power of any test is determined by both its sensitivity and its specificity.[19][20][21]
The tradeoff between specificity and sensitivity is explored in ROC analysis as a trade off between TPR and FPR (that is, recall and fallout).[22] Giving them equal weight optimizes informedness = specificity + sensitivity − 1 = TPR − FPR, the magnitude of which gives the probability of an informed decision between the two classes (> 0 represents appropriate use of information, 0 represents chance-level performance, < 0 represents perverse use of information).[23]
Sensitivity index[edit]
The sensitivity index or d′ (pronounced «dee-prime») is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, compared against the standard deviation of the noise distribution. For normally distributed signal and noise with mean and standard deviations 



[24]
An estimate of d′ can be also found from measurements of the hit rate and false-alarm rate. It is calculated as:
- d′ = Z(hit rate) − Z(false alarm rate),[25]
where function Z(p), p ∈ [0, 1], is the inverse of the cumulative Gaussian distribution.
d′ is a dimensionless statistic. A higher d′ indicates that the signal can be more readily detected.
Confusion matrix[edit]
The relationship between sensitivity, specificity, and similar terms can be understood using the following table. Consider a group with P positive instances and N negative instances of some condition. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as well as derivations of several metrics using the four outcomes, as follows:
| Predicted condition | Sources: [26][27][28][29][30][31][32][33][34]
|
||||
| Total population = P + N |
Positive (PP) | Negative (PN) | Informedness, bookmaker informedness (BM) = TPR + TNR − 1 |
Prevalence threshold (PT) = 
|
|
|
Actual condition |
Positive (P) | True positive (TP), hit |
False negative (FN), type II error, miss, underestimation |
True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR |
False negative rate (FNR), miss rate = FN/P = 1 − TPR |
| Negative (N) | False positive (FP), type I error, false alarm, overestimation |
True negative (TN), correct rejection |
False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR |
True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR |
|
| Prevalence = P/P + N |
Positive predictive value (PPV), precision = TP/PP = 1 − FDR |
False omission rate (FOR) = FN/PN = 1 − NPV |
Positive likelihood ratio (LR+) = TPR/FPR |
Negative likelihood ratio (LR−) = FNR/TNR |
|
| Accuracy (ACC) = TP + TN/P + N | False discovery rate (FDR) = FP/PP = 1 − PPV |
Negative predictive value (NPV) = TN/PN = 1 − FOR | Markedness (MK), deltaP (Δp) = PPV + NPV − 1 |
Diagnostic odds ratio (DOR) = LR+/LR− | |
| Balanced accuracy (BA) = TPR + TNR/2 | F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN |
Fowlkes–Mallows index (FM) = 
|
Matthews correlation coefficient (MCC) =  
|
Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP |
- view
- talk
- edit
- A worked example
- A diagnostic test with sensitivity 67% and specificity 91% is applied to 2030 people to look for a disorder with a population prevalence of 1.48%
| Fecal occult blood screen test outcome |
|
||||
| Total population (pop.) = 2030 |
Test outcome positive | Test outcome negative | Accuracy (ACC)
= (TP + TN) / pop. |
F1 score
= 2 × precision × recall/precision + recall |
|
| Patients with bowel cancer (as confirmed on endoscopy) |
Actual condition positive |
True positive (TP) = 20 (2030 × 1.48% × 67%) |
False negative (FN) = 10 (2030 × 1.48% × (100% − 67%)) |
True positive rate (TPR), recall, sensitivity
= TP / (TP + FN) |
False negative rate (FNR), miss rate
= FN / (TP + FN) |
| Actual condition negative |
False positive (FP) = 180 (2030 × (100% − 1.48%) × (100% − 91%)) |
True negative (TN) = 1820 (2030 × (100% − 1.48%) × 91%) |
False positive rate (FPR), fall-out, probability of false alarm
= FP / (FP + TN) |
Specificity, selectivity, true negative rate (TNR)
= TN / (FP + TN) |
|
| Prevalence
= (TP + FN) / pop. |
Positive predictive value (PPV), precision
= TP / (TP + FP) |
False omission rate (FOR)
= FN / (FN + TN) |
Positive likelihood ratio (LR+)
= TPR/FPR |
Negative likelihood ratio (LR−)
= FNR/TNR |
|
| False discovery rate (FDR)
= FP / (TP + FP) |
Negative predictive value (NPV)
= TN / (FN + TN) |
Diagnostic odds ratio (DOR)
= LR+/LR− |
Related calculations
- False positive rate (α) = type I error = 1 − specificity = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- False negative rate (β) = type II error = 1 − sensitivity = FN / (TP + FN) = 10 / (20 + 10) ≈ 33%
- Power = sensitivity = 1 − β
- Positive likelihood ratio = sensitivity / (1 − specificity) ≈ 0.67 / (1 − 0.91) ≈ 7.4
- Negative likelihood ratio = (1 − sensitivity) / specificity ≈ (1 − 0.67) / 0.91 ≈ 0.37
- Prevalence threshold =
≈ 0.2686 ≈ 26.9%
This hypothetical screening test (fecal occult blood test) correctly identified two-thirds (66.7%) of patients with colorectal cancer.[a] Unfortunately, factoring in prevalence rates reveals that this hypothetical test has a high false positive rate, and it does not reliably identify colorectal cancer in the overall population of asymptomatic people (PPV = 10%).
On the other hand, this hypothetical test demonstrates very accurate detection of cancer-free individuals (NPV ≈ 99.5%). Therefore, when used for routine colorectal cancer screening with asymptomatic adults, a negative result supplies important data for the patient and doctor, such as ruling out cancer as the cause of gastrointestinal symptoms or reassuring patients worried about developing colorectal cancer.
Estimation of errors in quoted sensitivity or specificity[edit]
Sensitivity and specificity values alone may be highly misleading. The ‘worst-case’ sensitivity or specificity must be calculated in order to avoid reliance on experiments with few results. For example, a particular test may easily show 100% sensitivity if tested against the gold standard four times, but a single additional test against the gold standard that gave a poor result would imply a sensitivity of only 80%. A common way to do this is to state the binomial proportion confidence interval, often calculated using a Wilson score interval.
Confidence intervals for sensitivity and specificity can be calculated, giving the range of values within which the correct value lies at a given confidence level (e.g., 95%).[37]
Terminology in information retrieval[edit]
In information retrieval, the positive predictive value is called precision, and sensitivity is called recall. Unlike the Specificity vs Sensitivity tradeoff, these measures are both independent of the number of true negatives, which is generally unknown and much larger than the actual numbers of relevant and retrieved documents. This assumption of very large numbers of true negatives versus positives is rare in other applications.[23]
The F-score can be used as a single measure of performance of the test for the positive class. The F-score is the harmonic mean of precision and recall:
In the traditional language of statistical hypothesis testing, the sensitivity of a test is called the statistical power of the test, although the word power in that context has a more general usage that is not applicable in the present context. A sensitive test will have fewer Type II errors.
See also[edit]
- Brier score
- Cumulative accuracy profile
- Discrimination (information)
- False positive paradox
- Hypothesis tests for accuracy
- Precision and recall
- Receiver operating characteristic
- Statistical significance
- Uncertainty coefficient, also called proficiency
- Youden’s J statistic
Notes[edit]
- ^ There are advantages and disadvantages for all medical screening tests. Clinical practice guidelines, such as those for colorectal cancer screening, describe these risks and benefits.[35][36]
References[edit]
- ^ Yerushalmy J (1947). «Statistical problems in assessing methods of medical diagnosis with special reference to x-ray techniques». Public Health Reports. 62 (2): 1432–39. doi:10.2307/4586294. JSTOR 4586294. PMID 20340527. S2CID 19967899.
- ^ Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D.; Jurman G. (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D.; Toetsch N.; Jurman G. (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Chicco D.; Jurman G. (2023). «The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification». BioData Mining. 16 (1). doi:10.1186/s13040-023-00322-4. PMC 9938573.
- ^ Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215.
- ^ Saah AJ, Hoover DR (1998). «[Sensitivity and specificity revisited: significance of the terms in analytic and diagnostic language]». Ann Dermatol Venereol. 125 (4): 291–4. PMID 9747274.
- ^ Parikh, Rajul; Mathai, Annie; Parikh, Shefali; Chandra Sekhar, G; Thomas, Ravi (2008). «Understanding and using sensitivity, specificity and predictive values». Indian Journal of Ophthalmology. 56 (1): 45–50. doi:10.4103/0301-4738.37595. PMC 2636062. PMID 18158403.
- ^ a b Altman DG, Bland JM (June 1994). «Diagnostic tests. 1: Sensitivity and specificity». BMJ. 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
- ^ «SpPin and SnNout». Centre for Evidence Based Medicine (CEBM). Retrieved 18 January 2023.
- ^ Mangrulkar R. «Diagnostic Reasoning I and II». Retrieved 24 January 2012.
- ^ «Evidence-Based Diagnosis». Michigan State University. Archived from the original on 2013-07-06. Retrieved 2013-08-23.
- ^ «Sensitivity and Specificity». Emory University Medical School Evidence Based Medicine course.
- ^ Baron JA (Apr–Jun 1994). «Too bad it isn’t true». Medical Decision Making. 14 (2): 107. doi:10.1177/0272989X9401400202. PMID 8028462. S2CID 44505648.
- ^ Boyko EJ (Apr–Jun 1994). «Ruling out or ruling in disease with the most sensitive or specific diagnostic test: short cut or wrong turn?». Medical Decision Making. 14 (2): 175–9. doi:10.1177/0272989X9401400210. PMID 8028470. S2CID 31400167.
- ^ Pewsner D, Battaglia M, Minder C, Marx A, Bucher HC, Egger M (July 2004). «Ruling a diagnosis in or out with «SpPIn» and «SnNOut»: a note of caution». BMJ. 329 (7459): 209–13. doi:10.1136/bmj.329.7459.209. PMC 487735. PMID 15271832.
- ^ Fawcett, Tom (2006). «An Introduction to ROC Analysis». Pattern Recognition Letters. 27 (8): 861–874. Bibcode:2006PaReL..27..861F. doi:10.1016/j.patrec.2005.10.010. S2CID 2027090.
- ^ a b Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Gale SD, Perkel DJ (January 2010). «A basal ganglia pathway drives selective auditory responses in songbird dopaminergic neurons via disinhibition». The Journal of Neuroscience. 30 (3): 1027–37. doi:10.1523/JNEUROSCI.3585-09.2010. PMC 2824341. PMID 20089911.
- ^ Macmillan NA, Creelman CD (15 September 2004). Detection Theory: A User’s Guide. Psychology Press. p. 7. ISBN 978-1-4106-1114-7.
- ^
Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215. - ^
Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. - ^
Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. - ^
Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. - ^
Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8. - ^
Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17. - ^
Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477. - ^
Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410. - ^
Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003. - ^ Lin, Jennifer S.; Piper, Margaret A.; Perdue, Leslie A.; Rutter, Carolyn M.; Webber, Elizabeth M.; O’Connor, Elizabeth; Smith, Ning; Whitlock, Evelyn P. (21 June 2016). «Screening for Colorectal Cancer». JAMA. 315 (23): 2576–2594. doi:10.1001/jama.2016.3332. ISSN 0098-7484.
- ^ Bénard, Florence; Barkun, Alan N.; Martel, Myriam; Renteln, Daniel von (7 January 2018). «Systematic review of colorectal cancer screening guidelines for average-risk adults: Summarizing the current global recommendations». World Journal of Gastroenterology. 24 (1): 124–138. doi:10.3748/wjg.v24.i1.124. PMC 5757117. PMID 29358889.
- ^ «Diagnostic test online calculator calculates sensitivity, specificity, likelihood ratios and predictive values from a 2×2 table – calculator of confidence intervals for predictive parameters». medcalc.org.
Further reading[edit]
- Altman DG, Bland JM (June 1994). «Diagnostic tests. 1: Sensitivity and specificity». BMJ. 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
- Loong TW (September 2003). «Understanding sensitivity and specificity with the right side of the brain». BMJ. 327 (7417): 716–9. doi:10.1136/bmj.327.7417.716. PMC 200804. PMID 14512479.
External links[edit]
- UIC Calculator
- Vassar College’s Sensitivity/Specificity Calculator
- MedCalc Free Online Calculator
- Bayesian clinical diagnostic model applet
Статистические показатели эффективности теста двоичной классификации 
Чувствительность и специфичность — статистические показатели эффективности бинарной классификации теста, которые широко используются в медицине:
- Чувствительность измеряет долю положительных результатов, которые являются правильно (например, процент больных, у которых правильно определено какое-либо заболевание).
- Специфичность измеряет долю правильно идентифицированных отрицательных результатов (например, процент здоровых людей, которые правильно определены как не имеющие заболевания). какое-то заболевание).
Термины «положительный» и «отрицательный» относятся не к пользе, а к наличию или отсутствию состояния; например, если заболевание является заболеванием, «положительный» означает «больной», а «отрицательный» означает «здоровый».
Во многих тестах, включая диагностические медицинские тесты, чувствительность — это степень, в которой истинные положительные результаты не упускаются из виду, поэтому ложных отрицательных результатов мало, а специфичность — это степень, в которой классифицируются истинно отрицательные результаты. таким образом, ложных срабатываний немного. Чувствительный тест редко упускает из виду истинный положительный результат (например, не показывает ничего неправильного, несмотря на наличие проблемы); конкретный тест редко регистрирует положительную классификацию чего-либо, что не является целью тестирования (например, обнаружение одного вида бактерий и принятие его за другой, близкородственный, который является истинной целью).
Обычно существует компромисс между мерами. Например, в служба безопасности аэропорта, поскольку проверка пассажиров проводится на предмет потенциальных угроз безопасности, сканеры могут быть настроены на включение сигналов тревоги на предметах с низким уровнем риска, таких как пряжки ремня и ключи (низкая специфичность), чтобы увеличить вероятность обнаружения опасных объектов и минимизация риска пропуска объектов, которые действительно представляют угрозу (высокая чувствительность). Идеальный предсказатель будет на 100% чувствительным, что означает, что все больные правильно определены как больные, и на 100% специфичным, что означает, что ни один здоровый человек не будет неправильно идентифицирован как больной.
Термины «чувствительность» и «специфичность» были введены американским биостатистом Джейкобом Йерушалми в 1947 году.
Содержание
- 1 Определения
- 1.1 Применение в скрининговом исследовании
- 1.2 Матрица неточностей
- 2 Чувствительность
- 3 Специфичность
- 4 Графическое изображение
- 5 Медицинские примеры
- 5.1 Порог распространенности
- 5.2 Заблуждения
- 5.3 Индекс чувствительности
- 6 Рабочий пример
- 7 Оценка ошибок в указанной чувствительности или специфичности
- 8 Терминология в поиске информации
- 9 См. также
- 10 Примечания
- 11 Ссылки
- 12 Дополнительная литература
- 13 Внешние ссылки
Определения
В терминологии истина / ложь положительный / отрицательный, истина или ложь относится к присвоенной классификации, которая является правильной или неправильной, а положительная или отрицательная относится к отнесению к положительной или отрицательной категории.
Источники: Fawcett (2006), Powers (2011), Ting (2011), CAWCR D. Chicco G. Jurman (2020), Tharwat (2018). |
Применение к скрининговому исследованию
Представьте себе исследование, оценивающее тест, который проверяет людей на наличие болезни. Каждый человек, проходящий тест, либо болен, либо не болен. Результат теста может быть положительным (классифицируя человека как больного) или отрицательным (классифицируя человека как не болеющего). Результаты тестирования по каждому предмету могут совпадать, а могут и не соответствовать его фактическому статусу. В этой настройке:
- Истинно положительный: Больные люди правильно идентифицированы как больные
- Ложно-положительные: Здоровые люди неправильно определены как больные
- Истинно отрицательные: Здоровые люди правильно определены как здоровые
- Ложноотрицательный: Больные люди неправильно идентифицированы как здоровые
Матрица путаницы
Рассмотрим группу с P положительными случаями и N отрицательными случаями какого-либо состояния. Четыре исхода могут быть сформулированы в таблице 2 × 2 непредвиденных обстоятельств или матрице путаницы следующим образом:
| Истинное условие | |||||
| Общая совокупность | Условие положительное | Состояние отрицательное | Распространенность = Σ Состояние положительное / Σ Общая популяция | Точность (ACC) = Σ Истинно положительное + Σ Истинно отрицательное / Σ Общая популяция | |
| Прогнозируемое состояние | Прогнозируемое состояние. положительное | истинное положительное | ложное положительное,. ошибка типа I | положительное прогнозируемое значение (PPV), точность = Σ истинно положительное / Σ прогнозируемое условие положительный | Коэффициент ложного обнаружения (FDR) = Σ ложноположительный результат / Σ прогнозируемый положительный результат |
| прогнозируемое условие. отрицательный | ложноотрицательный,. ошибка типа II | истинно отрицательный | Коэффициент ложных пропусков (FOR) = Σ ложноотрицательный / Σ прогнозируемое отрицательное условие | отрицательное прогнозируемое значение (NPV) = Σ истинно отрицательное / Σ прогнозируемое отрицательное условие | |
| истинно положительное значение (TPR), Отзыв, Чувствительность, вероятность обнаружения, Мощность = Σ Истинно положительный результат / Σ Положительный результат | Частота ложных срабатываний (FPR), Выпадение, вероятность ложной тревоги = Σ Ложное срабатывание / Σ Условие отрицательное | Положительное отношение правдоподобия (LR +) = TPR / FPR | Диагностическое отношение шансов (DOR) = LR + / LR- | F1оценка = 2 · Точность · Отзыв / Точность + отзыв | |
| Частота ложноотрицательных (FNR), частота пропусков = Σ ложноотрицательные / Σ положительные условия | Специфичность (SPC), избирательность, истинно отрицательная частота (TNR) = Σ Истинно отрицательный / Σ Состояние отрицательное | Отрицательное отношение правдоподобия (LR−) = FNR / TNR |
Чувствительность
Рассмотрим пример медицинского теста для диагностики заболевания. Чувствительность относится к способности теста правильно определять больных, у которых действительно есть данное состояние. В примере с медицинским тестом, используемым для выявления заболевания, чувствительность (иногда также называемая степенью выявления в клинических условиях) теста — это доля людей, у которых положительный результат теста на заболевание, среди тех, у кого есть болезнь. Математически это может быть выражено как:
- чувствительность = количество истинно положительных результатов количество истинных положительных результатов + количество ложных отрицательных результатов = количество истинных положительных результатов общее количество больных людей в популяции = вероятность положительного результата теста при условии, что у пациента есть болезнь { displaystyle { begin {align} { text {чувствительность}} = { frac { text {количество истинных положительных результатов}} {{ text {количество истинных положительных результатов}} + { text {количество ложноотрицательные результаты}}}} \ [8pt] = { frac { text {количество истинных положительных результатов}} { text {общее количество больных людей в популяции}}} \ [8pt] = { text {вероятность положительного результата теста при условии, что пациент болен}} end {align}}}
Отрицательный результат теста с высокой чувствительностью полезен для исключения заболевания. Тест с высокой чувствительностью является надежным, если его результат отрицательный, поскольку он редко ставит неправильный диагноз тем, у кого есть болезнь. Тест со 100% чувствительностью распознает всех пациентов с заболеванием по положительному результату. Отрицательный результат теста окончательно исключает наличие заболевания у пациента. Тем не менее, положительный результат теста с высокой чувствительностью не обязательно полезен для определения болезни. Предположим, что «поддельный» тестовый набор всегда дает положительный результат. При использовании на больных пациентах все пациенты дают положительный результат, что дает 100% чувствительность теста. Однако чувствительность не учитывает ложные срабатывания. Фальшивый тест также дает положительный результат у всех здоровых пациентов, что дает ему 100% ложноположительный результат, что делает его бесполезным для обнаружения или «управления» заболеванием.
Чувствительность — это не то же самое, что точность или положительное прогнозируемое значение (отношение истинных положительных результатов к комбинированным истинным и ложным положительным результатам), что в такой же мере является утверждением о доля действительно положительных результатов в тестируемой популяции, поскольку речь идет о тесте.
При расчете чувствительности не учитываются неопределенные результаты испытаний. Если тест не может быть повторен, неопределенные образцы либо должны быть исключены из анализа (число исключений должно быть указано при цитировании чувствительности), либо их можно рассматривать как ложноотрицательные (что дает наихудшее значение чувствительности и, следовательно, может занижать его.).
Специфичность
Рассмотрим пример медицинского теста для диагностики заболевания. Специфичность относится к способности теста правильно отклонять здоровых пациентов без каких-либо заболеваний. Специфичность теста — это доля здоровых пациентов, у которых известно, что у них нет заболевания, у которых результат теста будет отрицательным. Математически это также может быть записано как:
- специфичность = количество истинных отрицательных результатов; количество истинных отрицательных результатов + количество ложных положительных результатов = количество истинных отрицательных результатов; общее количество здоровых особей в популяции = вероятность отрицательного результата при условии, что пациент хорошо { displaystyle { begin {align} { text {specificity}} = { frac { text {количество истинных отрицаний}} {{ text {количество истинных отрицаний}} + { text {количество ложные срабатывания}}}} \ [8pt] = { frac { text {количество истинно отрицательных результатов}} { text {общее количество здоровых особей в популяции}}} \ [8pt] = { text {вероятность отрицательного теста при условии, что пациент здоров}} end {align}}}
Положительный результат теста с высокой специфичностью полезен для определения болезни. У здоровых пациентов тест редко дает положительные результаты. Положительный результат означает высокую вероятность наличия заболевания.
Тест с более высокой специфичностью имеет более низкую частоту ошибок типа I.
Графическое изображение
Высокая чувствительность и низкая специфичность
Низкая чувствительность и высокая специфичность
Медицинские примеры
В медицинской диагностике чувствительность теста — это способность теста для правильного выявления людей с заболеванием (истинно положительный показатель), тогда как специфичность теста — это способность теста правильно идентифицировать тех, у кого нет заболевания (истинно отрицательный показатель). Если 100 пациентов, о которых известно, что у них есть заболевание, были протестированы, а 43 — положительными, то чувствительность теста составляет 43%. Если 100 тестируются без заболевания, а 96 дают полностью отрицательный результат, то специфичность теста 96%. Чувствительность и специфичность являются независимыми от распространенности характеристиками теста, поскольку их значения присущи самому тесту и не зависят от распространенности заболевания в интересующей популяции. Положительные и отрицательные прогностические значения, но не чувствительность или специфичность, являются значениями, на которые влияет распространенность заболевания в тестируемой популяции. Эти концепции проиллюстрированы графически в этом апплете Байесовская клиническая диагностическая модель, которая показывает положительные и отрицательные прогностические значения в зависимости от распространенности, чувствительности и специфичности.
Порог распространенности
Взаимосвязь между положительной прогностической ценностью скрининговых тестов и его целевой распространенностью пропорциональна — хотя и не линейна во всех случаях, а в одном конкретном случае. Следовательно, существует точка локальных экстремумов и максимальной кривизны, определяемая только как функция чувствительности и специфичности, за пределами которой скорость изменения прогностической ценности положительного теста падает с разной скоростью относительно распространенности заболевания. Эта точка была впервые определена с помощью дифференциальных уравнений Balayla et al. и называется порогом распространенности (ϕ e { displaystyle phi _ {e}}
- ϕ e = a (- b + 1) + b — 1 (a + b — 1) { displaystyle phi _ {e} = { frac {{ sqrt {a (-b + 1)}} + b-1} {(a + b-1)}}}
Где эта точка лежит на кривой экранирования имеет решающее значение для клиницистов и интерпретации положительных результатов скрининговых тестов в режиме реального времени.
Заблуждения
Часто утверждают, что высокоспецифический тест эффективен при лечении болезни при положительном результате, в то время как высокочувствительный тест считается эффективным для исключения болезни при отрицательном результате. Это привело к широко используемым мнемоникам SPPIN и SNNOUT, согласно которым высокоспецифичный тест sp, когда p положительный, управляет при заболевании (SP-P -IN), и высокий тест «senположительный», когда n исходные правила исключают заболевание (SN-N-OUT). Однако оба практических правила вводят в заблуждение, поскольку диагностическая сила любого теста определяется как его чувствительностью, так и его специфичностью.
Компромисс между специфичностью и чувствительностью исследуется в ROC-анализе как компромисс между TPR и FPR (то есть отзывами и последствиями). Придание им равного веса оптимизирует информированность = специфичность + чувствительность-1 = TPR-FPR, величина которой дает вероятность принятия обоснованного решения между двумя классами (>0 представляет надлежащее использование информации, 0 представляет собой шанс -уровневая производительность, <0 represents perverse use of information).
индекс чувствительности
индекс чувствительности или d ‘(произносится как «dee-prime») — это статистика, используемая в сигнале теория обнаружения. Она обеспечивает разделение между средними значениями сигнала и распределениями шума по сравнению со стандартным отклонением распределения шума. Для нормально распределенный сигнал и шум со средним и стандартным отклонениями μ S { displaystyle mu _ {S}}



- d ′ знак равно μ S — μ N 1 2 (σ S 2 + σ N 2) { displaystyle d ‘= { frac { mu _ {S} — mu _ {N}} { sqrt {{ fr ac {1} {2}} ( sigma _ {S} ^ {2} + sigma _ {N} ^ {2})}}}}
Оценка d ‘также может быть получена из измерений частота совпадений и ложных тревог. Он рассчитывается как:
-
- d ‘= Z (частота совпадений) — Z (частота ложных тревог),
где функция Z (p), p ∈ [0,1], является обратной для кумулятивное распределение Гаусса.
d ‘- это безразмерная статистика. Более высокий d ‘указывает на то, что сигнал может быть легче обнаружен.
Рабочий пример
- view
- talk
- Рабочий пример
- Диагностический тест с чувствительностью 67% и специфичностью 91% применяется к 2030 людям для поиска расстройства с распространенность среди населения 1,48%
| Пациенты с раком кишечника. (подтверждено эндоскопией ) | |||||
| Положительное состояние | Отрицательное состояние | Распространенность = (TP + FN) / Total_Population. = (20 + 10) / 2030. ≈ 1,48% | Точность (ACC) = (TP + TN) / Total_Population. = (20 + 1820) / 2030. ≈ 90,64% | ||
| Кал. скрытая. кровь. экран. тест. результат | Результат теста.. положительный | Истинно-положительный . (TP) = 20. (2030 x 1,48% x 67%) | Ложноположительный . (FP) = 180. (2030 x (100 — 1,48%) x (100 — 91%)) | Положительное прогнозируемое значение (PPV), Точность = TP / (TP + FP). = 20 / (20 + 180). = 10% | Коэффициент ложного обнаружения (FDR) = FP / (TP + FP). = 180 / (20 + 180). = 90,0% |
| Тест. результат. отрицательный | Ложно-отрицательный тив . (FN) = 10. (2030 x 1,48% x (100-67%)) | Истинно отрицательный . (TN) = 1820. (2030 x (100 -1,48%) x 91%) | Коэффициент ложных пропусков (FOR) = FN / (FN + TN). = 10 / (10 + 1820). ≈ 0,55% | Прогнозируемое отрицательное значение (NPV) = TN / (FN + TN). = 1820 / (10 + 1820). ≈ 99,45% | |
| TPR, Отзыв, Чувствительность = TP / (TP + FN). = 20 / (20 + 10). ≈ 66,7% | Частота ложных срабатываний (FPR), Fallout, вероятность ложной тревоги = FP / (FP + TN). = 180 / (180 + 1820). = 9,0% | Отношение положительного правдоподобия (LR +) = TPR / FPR. = (20/30) / (180/2000). ≈ 7,41 | Отношение шансов диагностики (DOR) = LR + / LR-. ≈ 20,2 | F1оценка = 2 · Точность · Отзыв / Точность + отзыв. ≈ 0,174 | |
| Уровень ложных отрицательных результатов (FNR), Частота промахов. = FN / (TP + FN). = 10 / (20 + 10). ≈ 33,3% | Специфичность, Избирательность, Истинно отрицательная скорость (TNR) = TN / (FP + TN). = 1820 / (180 + 1820). = 91% | Отношение отрицательного правдоподобия (LR-) = FNR / TNR. = (10/30) / (1820/2000). ≈ 0,366 |
Соответствующие вычисления
- Частота ложноположительных результатов (α) = ошибка типа I = 1 — специфичность = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- Ложноотрицательный результат коэффициент (β) = ошибка типа II = 1 — чувствительность = FN / (TP + FN) = 10 / (20 + 10) = 33%
- Мощность = чувствительность = 1 — β
- Отношение правдоподобия положительное = чувствительность / (1 — специфичность) = 0,67 / (1 — 0,91) = 7,4
- Отношение правдоподобия отрицательное = (1 — чувствительность) / специфичность = (1 — 0,67) / 0,91 = 0,37
- Порог распространенности = PT = TPR (- TNR + 1) + TNR — 1 (TPR + TNR — 1) { displaystyle PT = { frac {{ sqrt {TPR (-TNR + 1)}} + TNR-1} {(TPR + TNR-1)}}}
= 0,19 =>19,1%
Этот гипотетический скрининговый тест (анализ кала на скрытую кровь) правильно выявили две трети (66,7%) пациентов с колоректальным раком. К сожалению, учет показателей распространенности показывает, что этот гипотетический тест имеет высокий уровень ложноположительных результатов и не позволяет надежно идентифицировать рак прямой кишки в общей популяции бессимптомных людей (PPV = 10%).
С другой стороны, этот гипотетический тест демонстрирует очень точное обнаружение людей, свободных от рака (NPV = 99,5%). Таким образом, при использовании для рутинного скрининга колоректального рака у бессимптомных взрослых отрицательный результат дает важные данные для пациента и врача, такие как исключение рака как причины желудочно-кишечных симптомов или успокаивание пациентов, обеспокоенных развитием колоректального рака.
Оценка ошибок в указанной чувствительности или специфичности
Только значения чувствительности и специфичности могут вводить в заблуждение. Необходимо рассчитать чувствительность или специфичность «наихудшего случая», чтобы не полагаться на эксперименты с небольшим количеством результатов. Например, конкретный тест может легко показать 100% чувствительность, если тестируется по золотому стандарту четыре раза, но один дополнительный тест по золотому стандарту, который дал плохой результат, будет означать чувствительность только 80%. Обычный способ сделать это — указать доверительный интервал биномиальной пропорции, часто вычисляемый с использованием интервала оценок Уилсона.
Доверительные интервалы для чувствительности и специфичности могут быть вычислены, давая диапазон значений, в котором правильное значение находится на заданном уровне достоверности (например, 95%).
Терминология в поиске информации
В информационном поиске положительное прогнозное значение называется точность, а чувствительность называется отзыв. В отличие от компромисса между специфичностью и чувствительностью, эти меры не зависят от количества истинных негативов, которое обычно неизвестно и намного превышает фактическое количество релевантных и извлеченных документов. Это предположение об очень большом количестве истинно отрицательных результатов по сравнению с положительными редко встречается в других приложениях.
F-score может использоваться в качестве единственной меры эффективности теста для положительного класса. Оценка F — это среднее гармоническое точности и запоминания:
- F = 2 × точность × точность отзыва + отзыв { displaystyle F = 2 times { frac {{ text {precision} } times { text {вспомнить}}} {{ text {precision}} + { text {вспомнить}}}}}
На традиционном языке проверки статистических гипотез чувствительность теста называется статистической мощностью теста, хотя слово «мощность» в этом контексте имеет более общее использование, которое не применимо в данном контексте. Чувствительный тест будет иметь меньше ошибок типа II.
См. Также
- Оценка по Брайеру
- Кумулятивный профиль точности
- Ложноположительный парадокс
- Дискриминация
- Точность и отзыв
- Статистическая значимость
- Коэффициент неопределенности, также называемый профессиональным мастерством
- Статистика Юдена
Примечания
Ссылки
Далее чтение
Внешние ссылки
- Калькулятор UIC
- Калькулятор чувствительности / специфичности Vassar College
- Бесплатный онлайн-калькулятор MedCalc
- Байесовская модель клинической диагностической модели











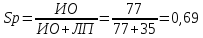




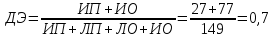





























![{displaystyle {begin{aligned}{text{sensitivity}}&={frac {text{number of true positives}}{{text{number of true positives}}+{text{number of false negatives}}}}\[8pt]&={frac {text{number of true positives}}{text{total number of sick individuals in population}}}\[8pt]&={text{probability of a positive test given that the patient has the disease}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12ec58e26222c7c528150ce69c86e2aa91ddc4c2)
![{displaystyle {begin{aligned}{text{specificity}}&={frac {text{number of true negatives}}{{text{number of true negatives}}+{text{number of false positives}}}}\[8pt]&={frac {text{number of true negatives}}{text{total number of well individuals in population}}}\[8pt]&={text{probability of a negative test given that the patient is well}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d48cee2cea0745bcc29d228f8c2783e4cb34547c)