Нахождение союзной матрицы
Для нахождения союзной матрицы выберите нужный размер исходной матрицы и заполните её элементы.
Другие онлайн калькуляторы
- Транспонирование матрицы
- Нахождение обратной матрицы
- Вычисление определителя матрицы
- Приведение матрицы к треугольному виду
- Возведение матрицы в степень
- Вычисление ранга матрицы
- Нахождение суммы элементов главной диагонали матрицы
- Сложение матриц
- Вычитание матриц
- Умножение матриц
- Умножение матрицы на число
Описание онлайн калькулятора
С помощью данного онлайн калькулятора Вы сможете найти союзную матрицу или проверить правильность своего решения.
Нахождение союзной матрицы выполнимо только в том случае, если матрица является квадратной.
Союзная матрица — это матрица, элементы которых являются алгебраическими дополнениями, соответствующих элементов исходной матрицы.
Описание работы онлайн калькулятора
- Минимальный размер матрицы 2х2;
- Максимальный размер матрицы 10х10;
- В поля ввода значений элементов матриц, можно вводить следующие типы чисел:
- Натуральные (0; 3; 9);
- Отрицательные (-43);
- Десятичные (1,5 или 1.5);
- Дробные (2/3).
- Максимальное количество вводимых символов 7;
- При нажатии кнопки «Вывести результат»
выводится результат требуемой операции.
Свои вопросы по работе данного онлайн калькулятора, Вы всегда можете задать в комментариях.
Онлайн калькулятор. Обратная матрицы методом алгебраических дополнений.
Используя этот онлайн калькулятор для вычисления обратной матрицы методом алгебраических дополнений, вы сможете очень просто и быстро найти обратную матрицу.
Воспользовавшись онлайн калькулятором для вычисления обратной матрицы методом алгебраических дополнений, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисления обратной матрицы, а также закрепить пройденный материал.
Найти обратную матрицу методом алгебраических дополнений
Размер матрицы:
Введите значения Матрицы:
A-1
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса).
Рассмотрим как найти обратную матрицу с помощью алгебраических дополнений.
Обратной матрицей называется матрицы A-1 при умножении на исходную матрицу A получается единичная матрица E.
A·A-1 = A-1 · A = E
Алгоритм нахождения обратной матрицы с помощью алгебраических дополнений:
- Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
- Найти матрицу миноров M.
- Из матрицы M найти матрицу алгебраических дополнений C*.
- Транспонировать матрицу (поменяем местами строки со столбцами) C*, получить матрицу C*T.
- По формуле найти обратную матрицу.
Пример
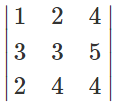
Рассмотрим данный метод на примере. Дана матрицы 3х3:
Найдем определитель (детерминант) матрицы, detA = 12 обратная матрица существует.
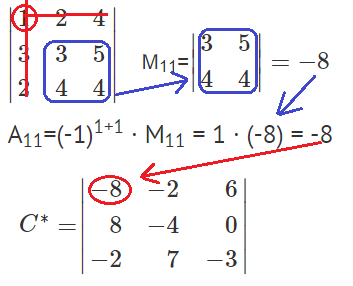
Найдем минор M11 и алгебраическое дополнение A11. В матрице А вычеркиваем строку 1 и столбец 1.
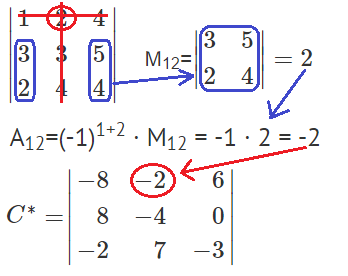
Найдем минор M12 и алгебраическое дополнение A12. В матрице А вычеркиваем строку 1 и столбец 2.
Остальные миноры и алгебраические дополнения находятся аналогично. В итоге получаем матрицу C*.
Найдем транспонированную союзную матрицу алгебраических дополнений C*T.
Найдем обратную матрицу. Ответ:
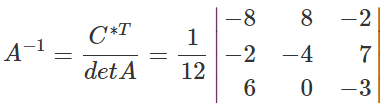
Союзная матрица онлайн
Назначение сервиса. С помощью онлайн калькулятора осуществляется расчет союзной матрицы. Результаты вычислений оформляются в отчете формата Word.
Инструкция. Для получения решения необходимо задать размерность матрицы. Далее в новом диалоговом окне заполните матрицу A.
Размерность матрицы
2345678910
Пример №1. Запишем матрицу в виде:
Главный определитель
∆=2•(9•2-0•8)-(-1•(6•2-0•5))+8•(6•8-9•5)=72
Определитель отличен от нуля, следовательно матрица является невырожденной и для нее можно найти обратную матрицу A-1.
Обратная матрица будет иметь следующий вид:
|
где Aij — алгебраические дополнения.
∆1,1=(9•2-0•8)=18
∆1,2=-(-1•2-8•8)=66
∆1,3=(-1•0-8•9)=-72
∆2,1=-(6•2-0•5)=-12
∆2,2=(2•2-8•5)=-36
∆2,3
=-(2•0-8•6)=48
∆3,1=(6•8-9•5)=3
∆3,2=-(2•8-(-1•5))=-21
∆3,3=(2•9-(-1•6))=24
Союзная матрица (взаимная, присоединённая).
Обратная матрица.
| A-1= |
|
Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.
E=A*A-1=
| (2•18)+(6•66)+(5•(-72)) | (2•(-12))+(6•(-36))+(5•48) | (2•3)+(6•(-21))+(5•24) |
| (-1•18)+(9•66)+(8•(-72)) | (-1•(-12))+(9•(-36))+(8•48) | (-1•3)+(9•(-21))+(8•24) |
| (8•18)+(0•66)+(2•(-72)) | (8•(-12))+(0•(-36))+(2•48) | (8•3)+(0•(-21))+(2•24) |
Пример №2.
Решение.
Главный определитель
∆ = 7∙(6∙3-1∙1)-(-2∙(-2∙3-1∙0.5))+1.5∙(-2∙1-6∙0.5)= 98.5
Транспонированная матрица
Алгебраические дополнения
∆1,1 = (6∙3-1∙1) = 17
∆1,2 = -(-2∙3-0.5∙1) = 6.5
∆1,3 = (-2∙1-0.5∙6) = -5
∆2,1 = -(-2∙3-1∙1.5) = 7.5
∆2,2 = (7∙3-0.5∙1.5) = 20.25
∆2,3 = -(7∙1-0.5∙(-2)) = -8
∆3,1 = (-2∙1-6∙1.5) = -11
∆3,2 = -(7∙1-(-2∙1.5)) = -10
∆3,3 = (7∙6-(-2∙(-2))) = 38
Обратная матрица
Нахождение обратной матрицы с помощью союзной матрицы — КиберПедия
|
Навигация: Главная Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов. .. Оснащения врачебно-сестринской бригады. Интересное: Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 6 из 11Следующая ⇒ Определение Матрица называется союзной к квадратной матрице , если элементы матрицы равны алгебраическим дополнениям соответствующих элементов матрицы . Имеет место следующее свойство: Тогда, если , то , а тогда Таким образом, матрица имеет союзную тогда и только тогда, когда она невырожденная. Пример Задание. Найти обратную матрицу к матрице Решение. Вычисляем определитель матрицы: Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле: Найдем союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы : Таким образом, Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером): Итак, Ответ. КОМПЛЕКСНЫЕ ЧИСЛА Историческая справка Исторически комплексные числа впервые были введены в связи с выведением формулы вычисления корней кубического уравнения . Хотя согласно некоторым источникам, по-видимому, мнимые величины были впервые упомянуты в 1545 году в известном труде «Великое искусство, или об алгебраических правилах» итальянского математика, инженера, философа, медика и астролога Джероламо Кардано (1501 — 1576), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40. Выражения, представимые в виде , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в 16-17 вв. с подачи французского философа, математика, механика, физика и физиолога Рене Декарта (1596-1650), который называл их так, отвергая их реальность. Одним из способов построения множества комплексных чисел состоит в том, что множество действительных чисел расширяют присоединением к этому множеству корня уравнения . Продолжительное время стоял вопрос, является ли множество комплексных чисел замкнутым, то есть все ли операции над комплексными числами являются приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней -ой степени из рассматриваемого комплексного числа была решена в работах английского математика Абрахама де Муавра (1667 — 1754) в 1707 году и английского математика и философа Роджера Котса (1682 — 1716) в 1722 году. Символ для обозначения мнимой единицы предложил швейцарский, немецкий и российский математик и механик Леонардо Эйлер в 1777, взявший для этого первую букву латинского слова «imaginarius» — мнимый. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Понятие комплексного числа Определение Комплексным числом называется выражение вида Например. ⇐ Предыдущая12345678910Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. |
Обратная матрица.
Навигация по странице:
- Определение обратной матрицы
- Свойства обратной матрицы
- Методы вычисления обратной матрицы
- Вычисления обратной матрицы с помощью присоединённой матрицы
- Вычисления обратной матрицы с помощью союзной матрицы
Онлайн калькулятор. Обратная матрица с помощью присоединённой матрицы.
Онлайн калькулятор. Обратная матрица с помощью союзной матрицы.
Определение.
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A-1 = A-1·A = E
Замечание.
Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Свойства обратной матрицы
| ● | |
| ● | (A·B)-1 = A-1·B-1 |
| ● | (A-1)T = (AT)-1 |
| ● | |
| ● | (A-1)-1 = A |
Методы вычисления обратной матрицы
Вычисление обратной матрицы с помощью присоединённой матрицы
Теорема.
Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.
Замечание.
Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.
Пример 1.
Найти обратную матрицу матрицы A
| A = | 2 | 4 | 1 | ||
| 0 | 2 | 1 | |||
| 2 | 1 | 1 |
Решение: Приписываем к матрице A справа единичную матрицу третьего порядка:
| A|E = | 2 | 4 | 1 | 1 | 0 | 0 | ~ | ||
| 0 | 2 | 1 | 0 | 1 | 0 | ||||
| 2 | 1 | 1 | 0 | 0 | 1 |
Преобразуем левую часть полученной матрицы в единичную.
| ~ | 2 | 4 | 1 | 1 | 0 | 0 | ~ | ||
| 0 | 2 | 1 | 0 | 1 | 0 | ||||
| 2 — 2 | 1 — 4 | 1 — 1 | 0 — 1 | 0 — 0 | 1 — 0 |
| ~ | 2 | 4 | 1 | 1 | 0 | 0 | ~ | ||
| 0 | 2 | 1 | 0 | 1 | 0 | ||||
| 0 | -3 | 0 | -1 | 0 | 1 |
Третью строку поделим на (-3) и поменяем местами со второй строкой:
| ~ | 2 | 4 | 1 | 1 | 0 | 0 | ~ | ||
| 0 | 2 | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 |
| ~ | 2 | 4 | 1 | 1 | 0 | 0 | ~ | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | ||||
| 0 | 2 | 1 | 0 | 1 | 0 |
Отнимем он 1-ой строки 2-ую умноженную на 4; от 3-тей строки 2-ую умноженную на 2:
| ~ | 2 — 4·0 | 4 — 4·1 | 1 — 4·0 | 1 — 4·(1/3) | 0 — 4·0 | 0 — 4·(-1/3) | ~ | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | ||||
| 0 — 2·0 | 2 — 2·1 | 1 — 2·0 | 0 — 2·1/3 | 1 — 2·0 | 0 — 2·(-1/3) |
| ~ | 2 | 0 | 1 | -1/3 | 0 | 4/3 | ~ | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | ||||
| 0 | 0 | 1 | -2/3 | 1 | 2/3 |
Отнимем он 1-ой строки 3-ую строку:
| ~ | 2 — 0 | 0 — 0 | 1 — 1 | -1/3 — (-2/3) | 0 — 1 | 4/3 — 2/3 | ~ | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | ||||
| 0 | 0 | 1 | -2/3 | 1 | 2/3 |
| ~ | 2 | 0 | 0 | 1/3 | -1 | 2/3 | ~ | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | ||||
| 0 | 0 | 1 | -2/3 | 1 | 2/3 |
Разделим 1-ую строку на 2:
| ~ | 1 | 0 | 0 | 1/6 | -1/2 | 1/3 | ||
| 0 | 1 | 0 | 1/3 | 0 | -1/3 | |||
| 0 | 0 | 1 | -2/3 | 1 | 2/3 |
| Ответ: A-1 = | 1/6 | -1/2 | 1/3 | ||
| 1/3 | 0 | -1/3 | |||
| -2/3 | 1 | 2/3 |
Вычисление обратной матрицы с помощью союзной матрицы
Определение.
Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.
Пример 1.
Найти обратную матрицу матрицы A
| A = | 2 | 4 | 1 | ||
| 0 | 2 | 1 | |||
| 2 | 1 | 1 |
Решение: Найдем определитель матрицы A:
| det(A) = | 2 | 4 | 1 | = |
| 0 | 2 | 1 | ||
| 2 | 1 | 1 |
= 2·2·1 + 4·1·2 + 1·0·1 — 1·2·2 — 2·1·1 — 4·0·1 = 4 + 8 + 0 — 4 — 2 — 0 = 6
Найдем алгебраические дополнения матрицы A:
| A11 = (-1)1 + 1· | 2 | 1 | = 2·1 — 1·1 = 1 |
| 1 | 1 |
| A12 = (-1)1 + 2· | 0 | 1 | = -(0·1 — 1·2) = 2 |
| 2 | 1 |
| A13 = (-1)1 + 3· | 0 | 2 | = 0·1 — 2·2 = -4 |
| 2 | 1 |
| A21 = (-1)2 + 1· | 4 | 1 | = -(4·1 — 1·1) = -3 |
| 1 | 1 |
| A22 = (-1)2 + 2· | 2 | 1 | = 2·1 — 1·2 = 0 |
| 2 | 1 |
| A23 = (-1)2 + 3· | 2 | 4 | = -(2·1 — 4·2) = 6 |
| 2 | 1 |
| A31 = (-1)3 + 1· | 4 | 1 | = 4·1 — 1·2 = 2 |
| 2 | 1 |
| A32 = (-1)3 + 2· | 2 | 1 | = -(2·1 — 1·0) = -2 |
| 0 | 1 |
| A33 = (-1)3 + 3· | 2 | 4 | = 2·2 — 4·0 = 4 |
| 0 | 2 |
Запишем союзную матрицу:
| Ã = | 1 | 2 | -4 | ||
| -3 | 0 | 6 | |||
| 2 | -2 | 4 |
Найдем обратную матрицу:
|
|
= |
|
| Ответ: A-1 = | 1/6 | -1/2 | 1/3 | ||
| 1/3 | 0 | -1/3 | |||
| -2/3 | 1 | 2/3 |
Онлайн калькуляторы с матрицами.
Упражнения с матрицами.
Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Операции над отношениями
Поскольку бинарные отношения, определенные на паре множеств A и B , являются подмножествами декартова произведения A × B , мы можем выполнять над ними все обычные операции над множествами.
Пусть R и S — два отношения над множествами A и B соответственно.
Пересечение отношений
Пересечение отношений (R cap S) определяется
[R cap S = left{ {left({a,b} right) mid aRb text{and} aSb} right},]
, где (a in A) и (b in B.
Например, пусть (R) и (S) будут отношениями « является другом » и « является коллегой по работе «, определенными на множестве людей (A) (при условии (А = В)). Их пересечением (Rcap S) будет отношение « друг и коллега по работе «.
Если отношения (R) и (S) заданы матрицами ({M_R} = left[ {{a_{ij}}} right]) и ({M_S} = left [ {{b_{ij}}} right],) матрица их пересечения (R cap S) имеет вид
[{M_{R cap S}} = {M_R} * {M_S} = left[ {{a_{ij}} * {b_{ij}}} right],]
, где операция произведения выполняется как поэлементное умножение.
Союз отношений
Аналогично, объединение отношений (R cup S) определяется как
[R cup S = left{ {left( {a,b} right) mid aRb text{или } aSb} right},]
при условии (a in A) и (b in B.)
Например, объединение отношений « меньше » и « равно » на множестве целых чисел будет отношение « меньше или равно ».
Если отношения (R) и (S) заданы матрицами ({M_R} = left[ {{a_{ij}}} right]) и ({M_S} = left [ {{b_{ij}}} right],) объединение отношений (R cup S) задается следующей матрицей:
[{M_{R чашка S}} = {M_R} + {M_S} = left[ {{a_{ij}} + {b_{ij}}} right],]
где сумма элементов вычисляется по правилам
[0 + 0 = 0,;;1 + 0 = 0 + 1 = 1,;;1 + 1 = 1.]
Разница отношений
Разница двух отношений определяется следующим образом:
[R обратная косая черта S = left{ {left( {a,b} right) mid aRb text{а не} aSb} right},]
[S обратная косая черта R = left{ {left( {a,b} right) mid aSb text{а не } aRb} right},]
, где (a in A) и (b in B.)
Предположим, (A = left{ {a,b,c,d} right}) и (B = left{ {1,2,3} right}.) Соотношения (R) и (S) имеют вид
[R = left{ {left( {a,1} right),left( {b,2} right),left({c,3} right),left({ d,1} right)} right},;;S = left{ {left( {a,1} right),left({b,1} right),left ( {c,1} right),left( {d,1} right)} right}.
Тогда различия отношений (R backslash S) и (S backslash R) задаются как
[Rобратная косая черта S = left{ {left({b,2} right),left({c,3} right)} right},;;Sbackslash R = left{ {left( {b,1} right),left( {c,1} right)} right}.]
Симметричная разность отношений
Симметричная разность двух бинарных отношений (R) и (S) — это бинарное отношение, определенное как
[R ,треугольник, S = left( {R cup S} right)backslash left( {R cap S} right),;;text{or}; ;R ,треугольник, S = left( {Rbackslash S} right) cup left( {Sbackslash R} right).]
Пусть (R) и (S) отношения предыдущего примера. Затем
[R ,треугольник, S = left{ {left({b,2} right),left({c,3} right)} right} cup left { { влево ( {b, 1} вправо), влево ( {c, 1} вправо)} вправо } = влево { { влево ( {b, 1} вправо), влево ( {c,1} right),left( {b,2} right),left( {c,3} right)} right}.
Дополнение к бинарному отношению
Предположим, что (R) является бинарным отношением между двумя множествами (A) и (B).. Дополнением (R) над (A) и (B) является бинарное отношение отношение определено как
[ bar R = left{ {left( {a,b} right) mid text{not} aRb} right},]
, где (a in A) и (b in B.)
Например, пусть (A = left{ {1,2} right},) (B = left{ {1,2,3} right}.) Если отношение (R) между множествами (A) и (B) определяется как
[R = left{ {left( {1,2} right),left( {1,3} right),left( {2,2} right),left( { 2,3} справа)} справа},]
, то дополнение (R) имеет вид
[bar R = left{ {left( {1,1} right),left( {2,1} right)} right}.]
Обратное бинарное отношение
Пусть (R) — бинарное отношение на множествах (A) и (B). Обратное отношение или транспонирование (R) над (A) и (B) получается путем переключения порядка элементов: 9{-1}.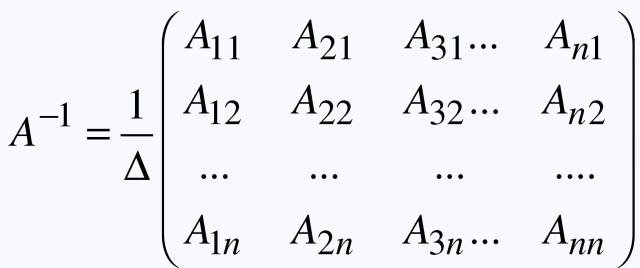
Пустые, универсальные и тождественные отношения
Отношение (R) между множествами (A) и (B) называется пустым отношением, если (R = varnothing.)
Универсальное отношение между множествами (A) и (B,), обозначаемое через (U,), есть декартово произведение множеств: (U = A times B.)
Отношение (R), определенное на множестве (A), называется тождественным отношением (обозначаемым через (I)) если (I = left{ {left( {a,a} справа) середина для всех а в А} справа}.)
Свойства комбинированных отношений
Когда мы применяем рассмотренные выше алгебраические операции, мы получаем комбинированное отношение. Исходные отношения могут обладать определенными свойствами, такими как рефлексивность, симметрия или транзитивность. Вопрос в том, сохранятся ли эти свойства в комбинированном отношении? В таблице ниже показано, какие бинарные свойства сохраняются в каждой из основных операций.
Рисунок 1.
См. решенные проблемы на стр. 2.
Как выполнить объединение и пересечение матриц?… любые кодировки
Вопросы: Как выполнить Matrix Union and Intersection
2022-10-06T09: 15: 39+00: 00 2022-10-06T09: 15: 39+00: 00
1111111111111111111111111111111111111111111111111111111111111119001er
111111111111111111111111111111111111111111111111111119. Предположим, что используется NumPy, учитывая две матрицы anycodings_numpy mat_A и mat_B: значение
свидание 2020-10-16 49.78 2020-10-15 50.30 2020-10-14 50.44 2020-10-13 50.85 2020-10-12 51.42 ... ... 08.01.2014 45.25 2014-01-07 45.18 2014-01-06 45.192014-01-03 45.21 2014-01-02 44.95
[1711 строк x 2 столбца]
значение свидание 2020-10-16 95.0 2020-10-15 95.0 2020-10-14 95.0 2020-10-13 95.0 2020-10-12 95.0 ... ... 2012-08-08 209,0 2012-08-07 209,0 2012-08-06 209,0 2012-08-03 209,0 2012-08-02 209,0
[1361 строк x 2 столбца]
Есть ли эффективный способ получить следующее значение anycodings_numpy?
- союз между
mat_Aиmat_B:- с использованием даты
- заполнение симметричной разницы между
mat_Aиmat_Bсо значением= Нет
- с использованием даты
- пересечение между
mat_Aиmat_B
Админы
PYTHONNUMPYMATRIX
Всего ответов 1
29
Ответы 1: Как выполнить матричное объединение и пересечение
Для пересечения вы можете использовать intersect1d
_, inter, _ = numpy.intersect1d(a[:, 0], b[:, 0], accept_unique =Истина, return_indices=Истина)
Что дает вам индексы a в b и anycodings_matrix наоборот.
И если anycodings_matrix вам не нужно поворачивать, то вы можете сделать anycodings_matrix трижды
_, интер 1, _ = numpy.intersect1d (a [:, 1], b [:, 1], accept_unique = True, return_indices = True) _, no_piv_inter, _ = numpy.intersect1d (inter1, inter2, accept_unique = True, return_indices = True)
Для симметричной разницы существует anycodings_matrix setxor1d
diff = numpy.setxor1d(a[:, 0], b[:, 0], accept_unique=True, return_indices=True)
Есть union1d. Но, похоже, anycodings_matrix не работает в вашем случае, потому что anycodings_matrix не возвращает индексы. Чтобы присоединиться, вы можете использовать anycodings_matrix vstack и unique.
v = numpy.vstack((a, b)) _, уникальный = numpy.unique (v [:, 0], ось = 0, return_index = True) союз = v[уникальный, :]
Затем вы можете заполнить разницу
diff_idx = numpy.in1d(union[:, 0], diff, accept_unique=True) объединение [diff_idx, 0] = Нет
Я не запускал все коды.
Этот способ неэффективен с точки зрения сложности anycodings_matrix. Я считаю, что структура данных anycodings_matrix неверна. Для запрошенной операции anycodings_matrix хэш-таблица, которая является dict в python anycodings_matrix, предпочтительнее. Но эти пустые операции anycodings_matrix должны быть быстрыми по сравнению с циклами anycodings_matrix.
0
2022-10-06T09:15:39+00:00 2022-10-06T09:15:39+00:00 Ссылка для ответа
мРахман
Темы с самым высоким рейтингом
Python — интерполяция значений фрейма данных
Как экспортировать текущее форматированное время из нескольких часовых поясов в текстовый файл
Ошибка реакции: TypeError: props.
Динамическая сортировка вызывает ошибку выражения LINQ невозможно перевести
Как выровнять изображения при любой ориентации изображений
Javascript — изменить значение моего ввода в HTML на результат моей функции, используя событие onclick
Изменить с UID на ANR в запросе LDAP?
Как добавить новый столбец в фрейм данных после каждого n-го столбца и как сохранить имена столбцов, а не индекс?
Как перетащить вместе все узлы и соединения
Проблема флаттера: не удалось разрешить все артефакты для конфигурации ‘: classpath’
Доступ к Spark Значение объекта Row
Могу ли я обновить до Python 3.9 или 3.10 в базе Anaconda (root)?
В Fabricjs. как центрировать подобъекты группы на холсте
Имя файла журнала PowerShell с проблемой даты и времени
Как обернуть контейнер div вокруг таблицы Ckeditor при вставке
Как вставить байты в массив со сдвигом?
Как рассчитать количество строк (и их процент), которые находятся ниже 10-го процентиля столбца в SQL?
Изменение прав пользователя в базе данных Informix
Подпроцесс Python.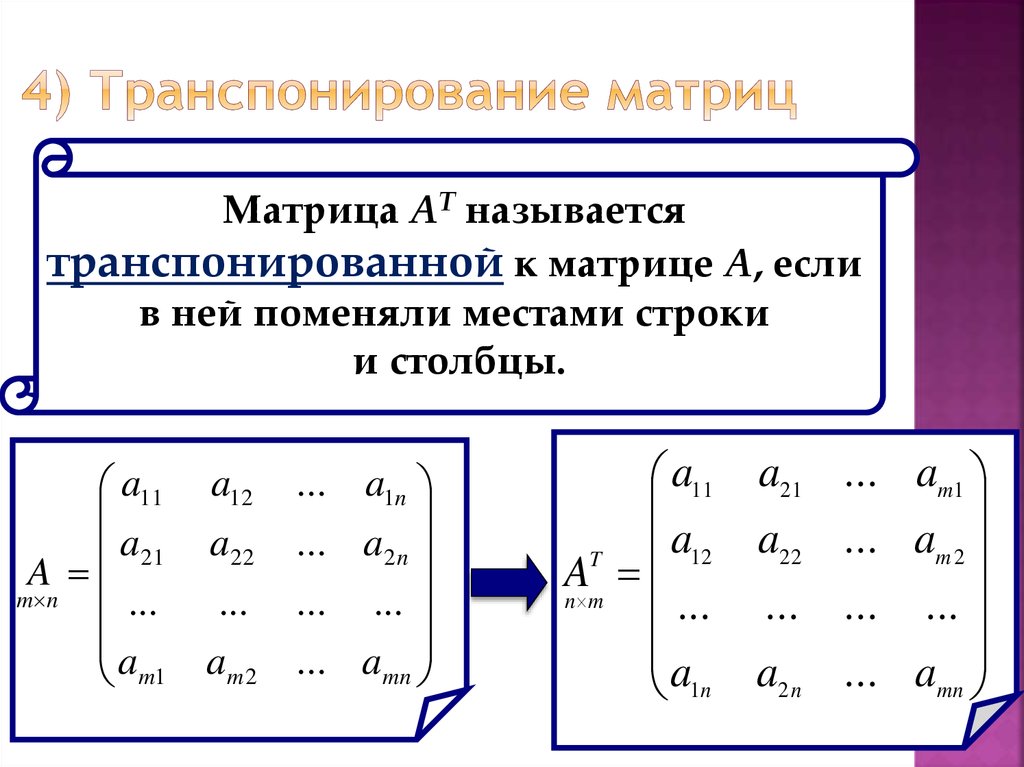
Есть ли способ поделиться переменными среды и секретами между лямбда-функциями в Amplify?
Разбор ПЛАНА ЗАПРОСА для возврата определенных результатов
Firebase, который является правильным способом установки кеша
Переопределить тип элемента в React
Matplotlib, что отображать в цикле с пользовательским вводом
Регистрация Linq.Expression.Optimizer работать по всему миру
Алгоритм топологической сортировки Кана BFS или DFS
Защищенный лист VBA предотвращает замену текста макросом, но ячейки не защищены
Django получает отдельные записи в таблице, кажется, выбирает случайную строку
Приложение Laravel отображает структуру файла laravel при доступе в браузере
Azure AD назначает роль другим пользователям организации
Использование колес с пакетом развертывания aws lambda
FiveM ‘then’ ожидается рядом со ‘=’
Tkinter, Checkbutton, один и тот же код имеет другой результат в def или в одном файле
Понимание использования «ожидания» в асинхронных методах
Как рассчитать процент роста количества клиентов в динамической дате
Использование gitpython для получения текущего хэша не работает при использовании qsub для отправки задания в кластере
Flutter web showDialog с маршрутом (url)
Преобразование JOLT, необходимое для удаления элемента из массива JSON
Отображение неправильных данных в текстовом поле с данными
Как зафиксировать событие изменения диапазона в TinyMCE?
Добавление цифровой подписи к документу Word с использованием формата Open XML в C#
Сравнение значений словаря со списком и возврат ключа
WordPress Archives Title Issue
Импорт файла из папки ресурсов (собственный .
Могу ли я прикрепить сценарий JS в виде текста в электронном письме?
Jenkins: агрегирование результатов построения матрицы
Как обновить пользовательский интерфейс после закрытия PopupMenuItem во флаттере
Как получить PDF-файл из фильтра намерений — Android
Создать новый столбец данных в таблице данных C# и заполнить его строки серийным номером на основе другого столбца в той же таблице данных
Как написать условную явную зависимость в Terraform
Торговые единицы и контракты | UCnet
Калифорнийский университет усердно работает над налаживанием профессиональных отношений и заключением справедливых соглашений с 15 профсоюзами, представляющими более 115 172 наших сотрудников. Университет стремится предоставить одни из самых привлекательных компенсаций, льгот и возможностей, которые делают его предпочтительным работодателем.
Ниже вы найдете подробную информацию о текущих переговорах и существующих трудовых договорах с каждой переговорной единицей.
Пенсионные пособия
На своем заседании в марте 2016 г. Попечительский совет Калифорнийского университета утвердил новую пенсионную программу для будущих сотрудников Калифорнийского университета в рамках более широких усилий по поддержанию передового опыта университета и его долгосрочного финансового благополучия. Программа UC Retirement Choice Program вступила в силу 1 июля 2016 г. для соответствующих требованиям новых сотрудников.
Пенсионные выплаты работникам, представленным профсоюзом, определяются в процессе коллективных переговоров. Калифорнийский университет достиг договоренностей с несколькими профсоюзами о принятии пенсионной программы выбора, как указано регентами. UC будет добросовестно вести переговоры с другими профсоюзами. Пока процесс переговоров не будет завершен, на других членов профсоюзов будут распространяться положения их существующих трудовых договоров о выходе на пенсию.
Продолжаем серию калькуляторов про матрицы, предыдущие калькуляторы: Определитель (детерминант) матрицы, Транспонирование матрицы, Умножение матриц.
Калькулятор ниже находит обратную матрицу с помощью метода Гаусса-Жордана. Раньше он вычислял обратную матрицу через союзную матрицу, но данный способ подходит только для матриц небольшого размера. Немного теории, как водится, под калькулятором.
Обратная матрица
Точность вычисления
Знаков после запятой: 2
Обратная матрица
Несколько определений:
Итак, обратная матрица — такая матрица, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Нахождение обратной матрицы через союзную матрицу выглядит следующим образом:
Союзная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы.
Ну и чтобы два раза не ходить —
Алгебраическое дополнение элемента матрицы A это число
где — определитель матрицы, получающейся из исходной матрицы A путем вычёркивания i -й строки и j -го столбца (дополнительный минор).
Соответственно, данных способ достаточно хорошо подходит для расчета обратных матриц вручную, при условии что размер матрицы 2х2, 3×3, или, максимум, 4×4. Дальше сложность этого метода сильно возрастает, и проще становится применять метод Гаусса-Жордана, но об этом как-нибудь в другой раз.

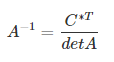
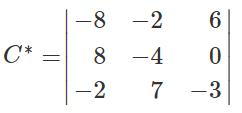
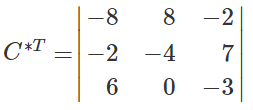



 Итальянский математик Никколо Фонтана Тартальей (1499 — 1557) в первой половине 16 века получил выражение для корня такого уравнения через некоторые параметры, для нахождения которых составляется система. Но было выяснено, что такая система не для всех кубических уравнений имела решение в действительных числах. Это непонятное на то время явление объяснил в 1572 году Рафаэль Бомбелли (1526 — 1572), что по сути было введением комплексных чисел и действий над ними. Но долгое время полученные результаты многими учеными считались сомнительными и лишь в 19 веке после появления трудов немецкого математика, механика, физика, астронома и геодезиста Карла Фридриха Гаусса (1777 — 1855) существование комплексных чисел стало общепризнанным.
Итальянский математик Никколо Фонтана Тартальей (1499 — 1557) в первой половине 16 века получил выражение для корня такого уравнения через некоторые параметры, для нахождения которых составляется система. Но было выяснено, что такая система не для всех кубических уравнений имела решение в действительных числах. Это непонятное на то время явление объяснил в 1572 году Рафаэль Бомбелли (1526 — 1572), что по сути было введением комплексных чисел и действий над ними. Но долгое время полученные результаты многими учеными считались сомнительными и лишь в 19 веке после появления трудов немецкого математика, механика, физика, астронома и геодезиста Карла Фридриха Гаусса (1777 — 1855) существование комплексных чисел стало общепризнанным.

 ..
..
 0
... ...
2012-08-08 209,0
2012-08-07 209,0
2012-08-06 209,0
2012-08-03 209,0
2012-08-02 209,0
0
... ...
2012-08-08 209,0
2012-08-07 209,0
2012-08-06 209,0
2012-08-03 209,0
2012-08-02 209,0
