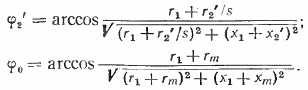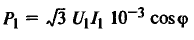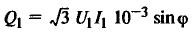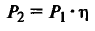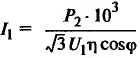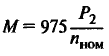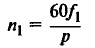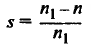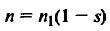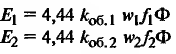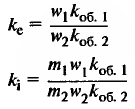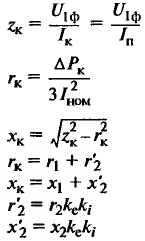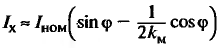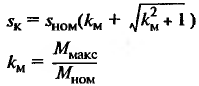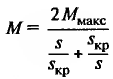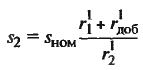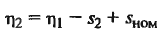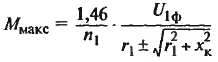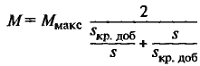Unit Converter
Enter the voltage and the current across the motor into the calculator to determine the motor winding resistance. This calculator can also determine the motor voltage or current when given the other variables.
- Nichrome Resistance Calculator
- Wire Resistance Calculator
- Wire Ampacity Calculator
- Resistivity Calculator
- Solenoid Force Calculator
The following equation is used to calculate the Motor Winding Resistance.
- Where R is the motor winding resistance (ohms)
- V is the voltage (volts)
- I is the current (amps)
To calculate a motor winding resistance, divide the motor voltage by the motor current.
What is Motor Winding Resistance?
Definition:
The motor winding resistance is the resistance inherent in the windings of an electrical machine. The higher the winding resistance, the less current will flow through the windings and thus cause less torque to be produced.
For example, if you are driving a machine that requires a maximum of 5 HP but has 8 HP motors available, you can use a 4-HP motor as long as it has a lower winding resistance than the other 8-HP motors. This will result in your machine operating at its maximum torque output of 5 HP, with only half of the required horsepower being used.
Lower winding resistance results in higher efficiency and better performance in general terms. An adequately designed motor should have an appropriate input voltage range, frequency, and whole-load currents for reliable operation over its service life.
To achieve this, it is necessary to know details about the power losses in the machine, including voltage drop in cables and current loss in windings, and other factors that affect performance and efficiency, such as ambient temperature and air circulation within the motor enclosure.
How to Calculate Motor Winding Resistance?
The most important thing in calculating Motor Winding Resistance is determining what type of windings are in use. This can sometimes be tricky as each manufacturer may use different types for their motors. It is also important to make sure that there are no short circuits in the winding, as this will also result in an incorrect calculation.
Once you have determined which type of windings are in your motor, you can begin calculating Motor Winding Resistance by using the following equations:
For slip ring motors: R = ρ L / (3.5 * N * R s )
Where: R = Resistance (Ω)
L = Length of wire (m)
N = Number of turns per coil
R s = Cross-sectional area (m2)
ρ = Resistivity factor of copper
Рабочие характеристики асинхронного двигателя — зависимости потребляемого тока I1 и мощности Р1, КПД, cos φ и скольжения s от полезной механической мощности P2. Эти характеристики определяются при постоянном напряжении U1 и частоте f1 сети.
Рабочие характеристики асинхронного двигателя могут быть получены экспериментально (опытным путем) и рассчитаны с помощью схемы замещения.
Ниже приводится расчет рабочих характеристик асинхронного двигателя по схеме замещения.
По обмотке статора асинхронной машины протекает многофазная система токов, обычно трехфазная, которая создает в воздушном зазоре машины вращающееся магнитное поле (магнитный поток Ф).
Вращающееся магнитное поле в свою очередь индуктирует (наводит) в проводниках обмотки ротора ЭДС, под действием которой в замкнутой накоротко обмотке ротора протекает ток I2. Этот ток, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение в сторону вращения магнитного поля.
Определим, с какой частотой вращения магнитное поле машины пересекает проводники ротора. Эта частота равна, об/мин:
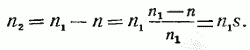
Определим частоту ЭДС f2, которая наводится магнитным полем асинхронной машины в проводниках ротора, Гц:
f2=р n2/60. (10)
Если учесть, что n2=n1s [см. формулу (9)], то можно записать
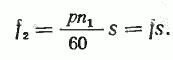
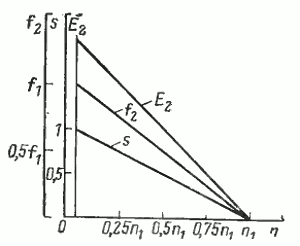
Из формулы (11) видно, что если ротор машины неподвижен (n=0, s=l), то частота ЭДС, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора ЭДС понижается и при синхронной частоте будет равна нулю. На рис. 13 показаны изменения скольжения, частоты и ЭДС в роторе в зависимости от частоты вращения ротора.
Рис. 13. Зависимость скольжения s, частоты f2 и ЭДС, наводимой в роторе, E2 от частоты вращения асинхронного двигателя n
Из закона электромагнитной индукции следует, что при гармоническом изменении магнитного поля наводимая в обмотке ЭДС равна:
E=4,44fwkобФmax, (12)
где f — электрическая частота, Гц; w — число последовательно соединенных витков фазы; kоб — обмоточный коэффициент; Фmax — максимальное значение рабочего потока, сцепленного с обмоткой, Вб.
Знание частоты f2 в роторе дает возможность определить ЭДС ротора Е2 при произвольной частоте вращения (скольжении), В, в виде
E2=4,44f2w2kоб2Фmax, (13)
где w2 — число последовательно соединенных витков обмотки ротора; kоб2 — обмоточный коэффициент ротора.
Подстановка f2 из формулы (11) дает, В,
E2s=4,44f s w2kоб2Фmax=sE2, ( 14)
где Е2 — ЭДС, наводимая в неподвижной обмотке ротора потоком Фmax, В.
Осветим теперь важный для анализа работы асинхронных двигателей вопрос о зависимости вращающегося магнитного потока двигателя от режима работы машины. Для этого, чтобы представить себе эту зависимость, определим вначале, какую ЭДС Е1 наводит этот поток в каждой фазе обмотки статора, В:
E1=4,44fw1kоб1Фmax, (15)
где w1 — число витков одной фазы статора; kоб1 —обмоточный коэффициент обмотки статора.
Напряжение U1, приложенное к статору, уравновешивается ЭДС E1 и падением напряжения I1z1 на внутреннем сопротивлении z1=r1+jx1 обмотки статора (х1— индуктивное сопротивление обмотки, определяемое потоком рассеяния) . При изменении нагрузки двигателя от нуля (холостой ход) до номинальной падение напряжения составляет 5—10 % приложенного. Таким образом, с достаточной для качественного анализа точностью можно полагать, что напряжение U1 полностью компенсируется ЭДС Е1 т. е. .
U1≈E1 (16)
Учитывая формулу (15), нетрудно заключить, что ЭДС и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фmах остается приблизительно постоянным независимо от изменения нагрузки двигателя.
Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие состоит в том, что вторичная магнитная цепь отделена от первичной воздушным зазором, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности, а магнитное поле вращающееся.
Как видно из формулы (14) и рис. 13, ЭДС, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Этот режим называется режимом короткого замыкания (КЗ). Ток статора в этом режиме называется током короткого замыкания и превышает его номинальный ток в 4—7 раз. Асинхронный двигатель в таких условиях нельзя длительно оставлять под полным напряжением из-за перегрева обмоток, который может привести к аварии.
Для определения тока короткого замыкания двигателя делают опыт КЗ. Этот опыт заключается в том, что к двигателю с заторможенным (неподвижным) ротором подводят пониженное напряжение, регулируя которое, устанавливают номинальный ток. Напряжение, подводимое к двигателю в опыте КЗ, оказывается малым (15— 20%) по сравнению с номинальным. На базе этого опыта можно в безопасных для двигателя условиях определить величину тока короткого замыкания /к при номинальном напряжении, А:
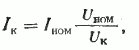
где Uном — номинальное напряжение, В; Uк — напряжение в опыте КЗ при номинальном токе, В; Iном — номинальный ток, А.
Замеряя в этом опыте по ваттметру мощность короткого замыкания Рк, подводимую к одной фазе двигателя, находят также коэффициент мощности в режиме КЗ
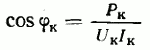
и эквивалентное активное сопротивление статора и ротора двигателя гк в режиме КЗ на одну фазу, Ом,
rк=Pк/Iном2 (19)
Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.
Определив угол φк по значению cosφк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:
хк=rкctgφк (20)
Индуктивное сопротивление хк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.
Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, так как мал вращающийся магнитный поток. Поэтому мощность Рк, которая подводится к машине, почти вся идет на нагрев проводников обмоток статора и ротора. То же самое можно сказать о режиме КЗ при полном напряжении.
Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и асинхронный двигатель подобен трансформатору, но уже в режиме холостого хода (XX). Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.
По обмотке статора при этом проходит ток холостого хода I0, который создает магнитодвижущую силу (МДС), необходимую для создания магнитного потока Фmax. Поскольку в магнитной цепи асинхронного двигателя имеется зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток XX составляет 25—35, а в двигателях малой мощности — 35—60% номинального тока.
Наводимая в неподвижном роторе ЭДС может быть определена по формуле (14), если учесть, что скольжение в этом режиме равно 1. Отношение ЭДС в обмотке статора к ЭДС в обмотке ротора называется коэффициентом трансформации ЭДС и может быть определено по формуле
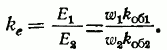
Мощность, потребляемая двигателем в режиме XX при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.
Важно заметить, что режим XX при неподвижном роторе очень близок к режиму, который возникает, когда асинхронный двигатель не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а скольжение примерно равно нулю [см. формулы (4), (9) и рис. 13]. Электродвижущая сила в роторе будет близкой к нулю, и, следовательно, подобно режиму XX при неподвижном роторе практически равен нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном МДС, необходимой для создания магнитного потока Фmax.
При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и вентиляционные. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное поле теперь очень медленно перемещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода оказываются близкими.
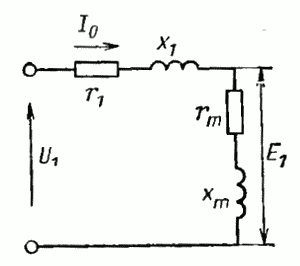
Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 14. Для определения параметров и характеристик двигателя помимо опыта КЗ выполняют опыт XX, во время которого замеряют ток обмотки статора I0 (А) и потребляемую мощность Р0 (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также коэффициент мощности XX:
cosφ0=P0/(UI0). (22)
Рис. 14. Схема замещения первичной цепи (статора) асинхронного двигателя, работающего в режиме холостого хода
Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты XX. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком ЭДС в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по (14). Ток ротора будет, очевидно, зависеть от ЭДС, наводимой в роторе, и сопротивления обмотки ротора, при этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора изменяется так же, как и ЭДС ротора E2s, Ом:
x2s=2πf2L2=s2πf1L2 =sx2, (23)
где L2 — индуктивность обмотки ротора, Гн; х2— индуктивное сопротивление рассеяния обмотки неподвижного ротора при s=l, Ом.
Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:
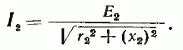
Учитывая (14) и (23), формулу (24) можно записать иначе:
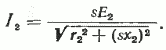
Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима XX при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения ЭДС ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.
Если разделить числитель и знаменатель выражения (25) для тока ротора I2 на s, то получим следующую формулу:
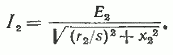
Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как и при вращающемся роторе. Удобство такого преобразования состоит в том, что оно позволяет вместо вращающегося ротора (вращающаяся вторичная электрическая цепь) рассматривать неподвижный ротор (неподвижная вторичная цепь).
Однако изучение процессов, происходящих в асинхронной машине, и расчет ее характеристик можно сделать более удобными, если заменить реальную обмотку ротора эквивалентной с числом витков в фазе и числом фаз, равным им у первичной обмотки (обмотки статора), т. е. вместо обмотки ротора с числом фаз m2, числом витков в фазе w2 и обмоточным коэффициентом kоб2 будем полагать, что обмотка ротора имеет число фаз ти число витков в фазе w1 и обмоточный коэффициент kоб1. Эта замена называется приведением обмотки ротора к обмотке статора. Нетрудно видеть, что магнитный поток Ф в этом случае будет наводить в эквивалентной (приведенной) обмотке ротора ЭДС, равную ЭДС обмотки статора E2‘=E1 (штрихом будем обозначать приведенные величины).
Замена обмотки ротора не должна привести к изменению потребляемой мощности, потерь, магнитодвижущей силы и фазы тока обмотки. Из этого условия определяются приведенные величины тока, активного и индуктивного сопротивлений обмотки ротора .
В соответствии с (13) имеем, В
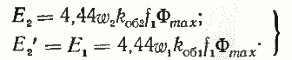
Из формул (27) вытекает отношение между ЭДС приведенной и реальной обмоток заторможенного ротора, которое называется коэффициентом трансформации ЭДС или напряжений. Он равен:
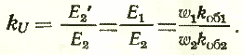
Из условия неизменности магнитодвижущих сил F2‘ =F2 следует, что
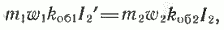
откуда вытекает отношение между токами, которое называется коэффициентом трансформации токов. Он равен:
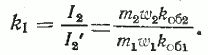
Из условия неизменности потерь в обмотке ротора при приведении следует, что
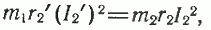
откуда
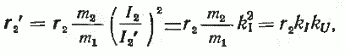
или r2‘=krr2,
где kr=kIkU — коэффициент приведения сопротивлений.
Из условия неизменности фазы тока обмотки ротора следует
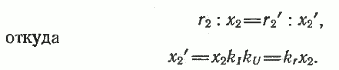
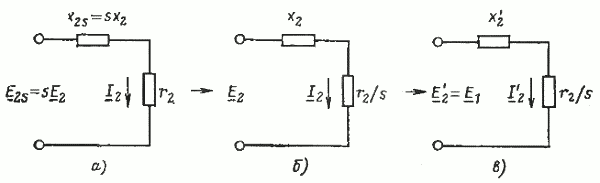
Процесс приведения цепи ротора показан на рис. 15. От схемы замещения обмотки вращающегося ротора (рис. 15,а) переходим к схеме замещения неподвижного ротора (рис. 15,б), а затем приводим обмотку ротора к обмотке статора (рис. 15, в).
Рис. 15. Схемы замещения: а — обмотки вращающегося ротора; б — неподвижного ротора; в — обмотки ротора, приведенной к обмотке статора
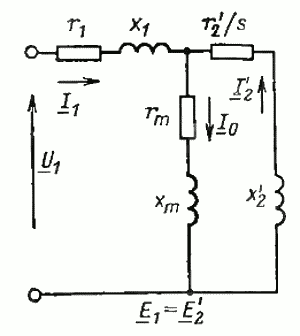
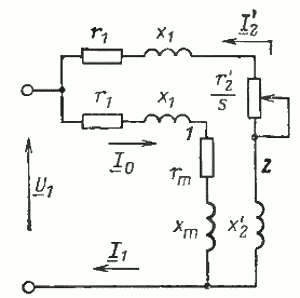
Поскольку теперь ЭДС Е1 первичной обмотки равна ЭДС Е2‘ вторичной обмотки, мы можем соединить электрически соответствующие точки схемы замещения обмотки статора и ротора. В результате получим схему замещения асинхронного двигателя, показанную на рис. 16. Здесь активное сопротивление rm отражает наличие потерь в стали двигателя. Для двигателей средней и большой мощности удобнее пользоваться упрощенной схемой замещения, приведенной на рис. 17.
Рис. 16. Т-образная схема замещения асинхронного двигателя
Рис. 17. Упрощенная Г-образная схема замещения асинхронного двигателя
Используя последнюю схему, легко найти токи и ЭДС в обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте n, по формуле (4)
и вычислить сопротивление r2‘/s в схеме по рис. 17. После этого нетрудно найти ток намагничивания I0 и приведенный ток I2‘ в роторной цепи, А:
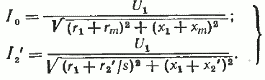
Это дает возможность вычислить электрические потери в обмотке статора трехфазного двигателя (m1=3), Вт:
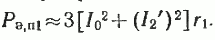
Электрические потери в обмотке ротора (Вт) можно найти, предварительно рассчитав по (30) приведенное сопротивление ротора r2‘ (Ом):
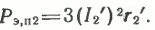
Суммарная активная мощность, передаваемая со статора на ротор, как видно из схемы (рис. 17), будет равна, Вт:
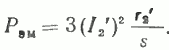
Эта мощность передается на ротор электромагнитным путем и поэтому называется электромагнитной мощностью.
Если из электромагнитной мощности вычесть мощность электрических потерь в обмотке ротора, то получим полную механическую мощность двигателя, Вт:
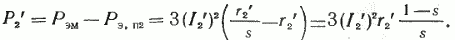
Полная механическая мощность расходуется на вращение приводного механизма (полезная механическая мощность) и на покрытие механических Рмх.п и добавочных Рд.п потерь самого двигателя. Поэтому полезная механическая мощность Р2 будет равна, Вт:
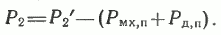
Коэффициент полезного действия двигателя по определению равен отношению отдаваемой (полезной механической) мощности к потребляемой (активной электрической) мощности. Разность между этими мощностями составляют потери в двигателе, равные, Вт:
где Pм.п=m1I02rm — магнитные потери или потери в стали. Таким образом, КПД двигателя равен:
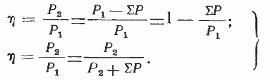
Использование первого или второго выражения для КПД определяется тем, какая из мощностей — P1 или Р2— известна. На практике наиболее часто применяется первое выражение (38).
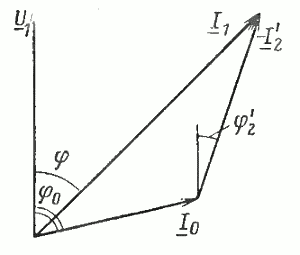
Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора, который равен сумме двух токов. Первый из них — это ток XX, который протекает по цепи 1 (рис. 17) и не изменяется при изменении частоты вращения ротора, второй — ток ротора I2‘, который определяется по (32). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 18. Углы φ2‘, φ0, необходимые для построения, можно найти с помощью схемы замещения (см. рис. 17):
Таким образом, знание параметров схемы замещения (r1, x1, r2‘, х2‘, rm, хm) и приложенного напряжения U1 (напряжение сети) позволяет с помощью приведенных выше формул определить полезную мощность, токи, потери, КПД, коэффициент мощности двигателя при различных скольжениях (частоте вращения).
Рис. 18. Диаграмма токов асинхронного двигателя
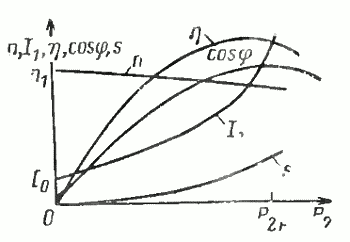
Зависимости потребляемого тока I1 и мощности Р1, КПД, cosφ и скольжения s от полезной механической мощности P2 носят название рабочих характеристик двигателя. Эти характеристики определяются при постоянном напряжении U1 и частоте f1 сети. Пример рабочих характеристик приведен на рис. 19.
Рис. 19. Рабочие характеристики асинхронного двигателя
Рассмотрим рабочие характеристики асинхронного двигателя. При холостом ходе (полезная мощность Р2—0) скольжение s также равно нулю (частота вращения ротора n практически равна синхронной), сопротивление r2/’s равно бесконечности (см. рис. 17) и ток I2‘==0. По обмотке статора протекает ток холостого хода I0. Коэффициент полезного действия η равен нулю, так как равна нулю полезная мощность Р2, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cosφ1=cosφ0).
При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление цепи 2 (см. рис. 17) и увеличивается ток ротора, а следовательно, и ток статоpa. Поскольку увеличивается полезная мощность, растет, КПД двигателя, а также коэффициент мощности.
Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 2—5%.
Поэтому скоростная характеристика n=f(P2) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s=f(P2) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение ЭДС, а также создание тока 1% в обмотке ротора и вращающего электромагнитного момента, под действием которого ротор приходит во вращение.
Характеристика cosφ=f(P2) лежит в области значений, меньших 1, так как асинхронный двигатель всегда потребляет ток I0, почти не зависящий от нагрузки в диапазоне мощностей от Р0 до Р2≈Рном. При XX обычно φ0<0,2, т. е. он содержит большую реактивную составляющую. При увеличении нагрузки cosφ быстро возрастает и достигает максимального значения при мощности Р2≈Р2ном. При увеличении нагрузки выше номинальной cosφ несколько снижается.
Коэффициент полезного действия достигает своего максимального значения при Р2≈ (0,6÷0,8)Р2ном и снижается при дальнейшем росте нагрузки. Поскольку двигатель обычно работает при переменной нагрузке, изменяющейся в пределах (0,6—1)Р2ном, то КПД в этом диапазоне изменения нагрузки должен быть достаточно высок.
Активное сопротивление
фазы обмотки статора двигателя с
короткозамкнутым ротором рассчитывается
так же, как и для двигателя с фазным
ротором.
Активное сопротивление
фазы короткозамкнутого ротора
определяется следующим образом. Как
говорилось выше, за фазу обмотки,
выполненной в виде беличьей клетки,
принимают один стержень и два участка
замыкающих колец (см. рис. 9,35). Токи в
стержнях и замыкающих кольцах
различны, поэтому их сопротивления при
расчете общего сопротивления фазы
должны быть приведены к одному току.
Таким образом, сопротивление фазы
короткозамкнутого ротора r2
является расчетным параметром, полученным
из условия равенства электрических
Рис. 9.51. Коэффициенты
к расчету проводимости
дифференциального
рассеяния:
а — коэффициент Δz в зависимости от
размерных соотношений bш/tzи bш/S;
б — коэффициент k’ в зависимости от
дробной части числа q;
в — коэффициент К’ в зависимости от
укорочения шага обмотки β;
г — коэффициент К»βв зависимости
от укорочения шага обмотки β и дробной
части числа q;
д — коэффициент k’скв зависимости
от соотношенияtz2/tz1и относительного скоса пазов βck
потерь в сопротивлении
r2
от тока I2
и суммарных потерь в стержне и участках
замыкающих колец соответственно от
тока в стержне Ic
и тока в замыкающем кольце Iкл
реальной машины:
(9.166)
где Iс
— ток в стержне ротора; Iкл
— ток в замыкающих кольцах; rC
— сопротивление стержня; rкл
— сопротивление участка замыкающего
кольца, заключенного между двумя
соседними стержнями (см. рис. 9.35).
Ток Iс
называют током ротора и в расчетах
обозначают I2.
Учитывая, что
Iкл
= Iс
/Δ
= I2
/Δ,
(9.167)
где
Δ
= 2sin
— (см.
§ 9.7), из
(9.167), получаем
r2
= rс
+ 2(9.168)
где
rc
=
;
(9.169)
rкл
=
(9.170)
В этих выражениях
Iс
— полная длина стержня, равная расстоянию
между замыкающими кольцами, м; Dкл.ср
— средний диаметр замыкающих колец, м
(см. рис. 9.37):
Dкл.ср
= D2
— hкл;
(9.171)
qc
— сечение стержня, м2;
kr
— коэффициент увеличения активного
сопротивления стержня от действия
эффекта вытеснения тока; при расчете
рабочих режимов в пределах изменения
скольжения от холостого хода до
номинального для всех роторов принимают
kr
= 1; qкл
— площадь поперечного сечения замыкающего
кольца, м2;
рс
и ркл
— соответственно удельные сопротивления
материала стержня и замыкающих колец,
Омм,
при расчетной температуре (см. табл.
5.1).
Сопротивление r2
для дальнейших расчетов должно быть
приведено к числу витков первичной
обмотки. Выражение коэффициента
приведения для сопротивления фазы
короткозамкнутого ротора получают,
подставляя в (9.151) значения m2
= Z2,
w2
= 1/2, kоб2
= 1 и учитывая влияние скоса пазов:

где коэффициент
скоса пазов (по 3.17)
kск
= 2
sin
;
Обычно значения
βск
выражают в долях зубцового деления
ротора tz2.
При скосе пазов ротора на одно зубцовое
деление статора γck
= π2p / Z1.
В этом случае в двигателях с 2р = 2 из-за
малости угла γck
принимают kcк
= 1.
Приведенное
значение активного сопротивления фазы
обмотки короткозамкнутого ротора
r‘2
=
r2
v12.
(9.173)
Индуктивное
сопротивление рассеяния обмотки статора
асинхронного двигателя с короткозамкнутым
ротором
рассчитывается по той же формуле, что
и для статора с фазными роторами, т. е.
x
= 1,58
(9.174)
Входящий в формулу
коэффициент магнитной проводимости
пазового рассеяния λп
определяют в зависимости от конфигурации
пазов по формулам табл. 9.26.
Коэффициент
магнитной проводимости лобового
рассеяния λл
определяется по (9.159).
Коэффициент
магнитной проводимости дифференциального
рассеяния λд1
определяют по формуле
(9.174а)
в которой ξ, находят
следующим образом.
При открытых пазах
статора и отсутствии скоса статора или
ротора
(9.175)
При полузакрытых
или полуоткрытых пазах статора с учетом
скоса пазов

В этих формулах
tz1
и tz2
— зубцовые деления статора и ротора;
ΔZ
определяют по кривой рис. 9.51, a,
kβ
определяют по (9.155) или (9.158); βcк
= βcк/tz2
— скос пазов, выраженный в долях зубцового
деления ротора. При отсутствии скоса
пазов bск
= 0; k’cк
определяют по кривым рис. 9.51, д в
зависимости от tz2/tz1
и βcк
(при отсутствии скоса пазов — по кривой,
соответствующей βск
= 0).
Индуктивное
сопротивление обмотки короткозамкнутого
ротора
определяют по формуле
(9.177)
полученной после
подстановки в (9.152) значений m2
= Z2
и q2
= 1/(2р) обмотки короткозамкнутого ротора
и введения дополнительного слагаемого
λск.
Коэффициент
магнитной проводимости пазового
рассеяния обмотки короткозамкнутого
ротора рассчитывают по приведенным в
табл. 9.27 формулам в зависимости от
конфигурации паза ротора (рис. 9.52).
Таблица 9.27. Расчетные
формулы для определения коэффициентов
магнитной
проводимости пазового рассеяния
короткозамкнутых роторов
|
Рисунок |
Расчетные |
|
9.52, |
|
|
9.52,6 |
|
|
9.52, |
|
|
9.52, |
|
|
9.52, |
|
При расчете
номинального режима двигателя во всех
формулах kд=
1.
При закрытых пазах
ротора любой конфигурации (рис. 9.52, а—д)
в расчетных формулах табл. 9.27 нужно при
шлицах по рис. 9.52, е слагаемые hш
/bш
заменить на 0,3 + 1,12 • 106,
по рис. 9.52, ж — наhш/bш
+ 1,12 • 106, где
— толщина ферромагнитной перемычки
над пазом, м;I2
— ток ротора, А.
Рис. 9.52. К расчету
коэффициентов магнитной проводимости
пазового рассеяния
короткозамкнутых роторов:
а — д — полузакрытые
пазы; е, ж — закрытые пазы
Коэффициент
магнитной проводимости лобового
рассеяния
рассчитывают в зависимости от размеров
и расположения замыкающих колец обмотки
по следующим формулам.
В роторах с литыми
обмотками при замыкающих кольцах,
прилегающих к торцам сердечника ротора
(см. рис. 9.37, б), используют формулу
(9.178)
Если замыкающие
кольца отставлены от торцов ротора (см.
рис. 9.37, а),
как, например, в обмотке, выполненной
из медных или латунных стержней, впаянных
в замыкающие кольца, расчет проводят
по формуле
(9.179)
В этих формулах
Dкл.ср
— средний диаметр замыкающих колец по
(9.171); Δ = 2 sin
πρ/Z2
— коэффициент приведения токов в кольце
к току в стержне; hкл
и bкл
— средние высота и ширина колец (см.
рис. 9.37);
;
— по (9.154).
Коэффициент
магнитной проводимости дифференциального
рассеяния обмотки, короткозамкнутого
ротора
(9.180)
где
(9.181)
ΔZ
находят по кривым рис. 9.51, а.
Как видно из
(9.181), при большом числе пазов ротора,
приходящихся на пару полюсов:
Z2/p
≥ 10, без заметной погрешности можно
принять ξ = 1.
Коэффициент
проводимости скоса,
учитывающий влияние на ЭДС обмотки
ротора скоса пазов,
,
(9.182)
где βск
— скос пазов, выраженный в зубцовых
делениях ротора. При скосе пазов на одно
зубцовое деление ротора βск
= 1; kμ
— коэффициент насыщения магнитной цепи
(по 9.129).
Приведенное к
числу витков обмотки статора индуктивное
сопротивление обмотки короткозамкнутого
ротора
х’2
= х2
γ12
(9.183)
где v12
— по (9.172).
Сопротивление
схемы замещения
rμ
(см. рис. 9.47, а) является расчетным.
Введением его в схему замещения учитывают
влияние потерь в стали статора на
процессы в асинхронной машине, поэтому
значение сопротивления rμ
должно быть принято таким, чтобы
выделяющаяся в нем активная мощность
была равна мощности, затрачиваемой на
потери в стали в реальной машине и
отнесенной к одной фазе. Таким образом,
rμ
= РСТ/(m
I20a
), так как активные потери в стали
определяются активной составляющей
тока холостого хода ,I0а.
Из схемы замещения rμ
=
где

Сопротивление
взаимной индукции обмоток статора и
ротора xμ
по схеме замещения может быть определено
как xμ
= Е1Iμ.
В расчетной практике
параллельное включение сопротивлений
rμ
и хμ
оказалось удобнее заменить последовательно
включенными сопротивлениями r12
и х12
(см. рис. 9.47, 6), значения которых определяют
из условия
откуда
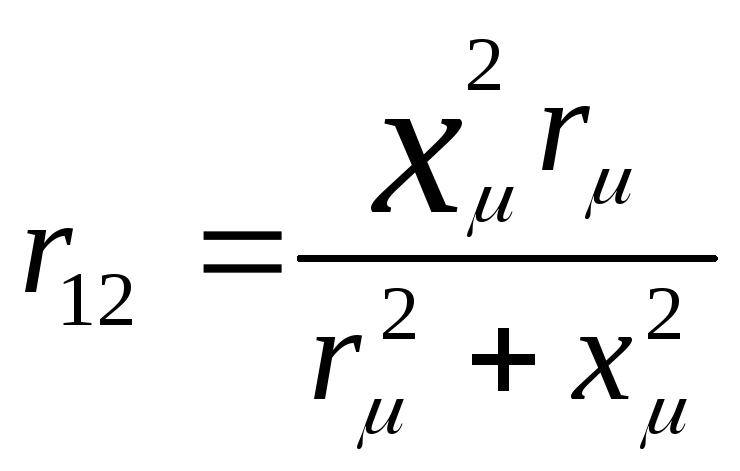
Так как в асинхронных
машинах rμ
≤ xμ,
то х12
≈ хμ,
а r12
<< х12.
В связи с этим значение r1
не играет заметной роли при анализе
процессов в машине, и в расчетах им часто
пренебрегают.
Сопротивления r1
и х12
с достаточной для обычных расчетов
точностью определяют по следующим
формулам:
r12
= Pcт.осн
/
(m I2μ)
; (9.184)
(9.185)
Расчетные формулы основных параметров асинхронных двигателей
В таблице 1 представлены расчетные формулы для определения основных параметров асинхронных двигателей.
В данной таблице собраны все формулы, которые касаются расчета параметров асинхронных двигателей.
Используя формулы из данной таблицы, вам больше не придется искать нужную формулу в различных справочниках.
Таблица 1 — Расчетные формулы для определения основных параметров асинхронных двигателей
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Потребляемая активная мощность из сети, кВт |
|
U1, I1 – линейные значения напряжения, В и тока двигателя, А; cosϕ – коэффициент мощности; |
| Потребляемая реактивная мощность, квар |
|
|
| Полезная мощность на валу, кВт |
|
Ƞ — КПД двигателя; |
| Потребляемый двигателем ток, А |
|
|
| Вращающий момент двигателя, кГм |
|
nном. – номинальная скорость вращения ротора, об/мин; |
| Синхронная скорость вращения магнитного поля, об/мин |
|
f1 – частота питающего тока, Гц; р – число пар полюсов машины; |
| Скольжение двигателя |
|
|
| Скорость вращения ротора при нагрузке, об/мин |
|
|
| ЭДС обмоток статора и ротора, В |
|
kоб.1, kоб.2 – обмоточные коэффициенты статора и ротора, равные произведению коэффициентов укорочения kу шага и распределения обмотки kw; kоб. = kу* kw; |
| Коэффициенты трансформации по напряжению и по току |
|
w1, w2 – числа витков обмоток статора и ротора; m1, m2 – числа фаз в обмотках статора и ротора. У двигателей с фазным ротором. m2 = 3 у двигателей с короткозамкнутым ротором; m2 = z2, т.е. числу пазов в роторе. |
| Параметры схемы замещения |
|
zк, rк, хк – полное, активное и индуктивное сопротивления при КЗ двигателя, Ом; Iп – пусковой ток двигателя, А; ∆Рк – суммарные потери в меди статора и ротора двигателя, Вт; r1, x1 – активное и индуктивное сопротивления обмотки статора, Ом; r2’, x2’ – активные и индуктивные сопротивления ротора, приведенные к обмотке статора, Ом; |
| Ток холостого хода, А |
|
Iном. – номинальный ток двигателя, А |
| Критическое скольжение |
|
sinϕ – коэффициент реактивной мощности; kм – коэффициент перегрузочной способности; |
| Уравнение вращающего момента |
|
Sном. – скольжение при номинальной нагрузке |
| Скольжение двигателя s2 при введении добавочного сопротивления в ротор |
|
|
| КПД двигателя при введении добавочного сопротивления в ротор |
|
|
| Критический максимальный момент, развиваемый в двигательном (+) и генераторном (-) режимах, кГм |
|
U1ф – фазное напряжение, В |
| Уравнение вращающего момента при добавочном сопротивлении в цепи ротора |
|
|
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
активное сопротивление двигателя, полное сопротивление двигателя, реактивное сопротивление двигателя, ток двигателя
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Содержание
- 1 Сопротивление обмоток. Начнем с основ
- 1.1 Электросопротивление, понятие проводимости
- 1.2 Что влияет на величину сопротивления, которое выдает проводник: коротко о материале, размерах и температуре
- 2 Измерение сопротивления обмотки электроприводов
- 2.1 Зачем проверять сопротивление обмоток в электроприводе
- 2.2 Приборы, которыми измеряют сопротивление
- 3 Работа и устройство однофазного асинхронного двигателя
- 3.1 Как происходит запуск
- 3.2 По какому принципу работает
- 3.3 Механизм работы
- 3.3.1 Проверка конденсатора мультиметром
- 3.4 Схема для подключения
- 4 Как определить рабочую и пусковую обмотки, измерив сопротивление их выводов
- 5 Подведем итог
Однофазные двигатели стали популярными из-за низкой стоимости и простых правил эксплуатации. Но они все же требуют к себе немного внимания, например, периодического измерения сопротивления обмоток. К тому же, такая процедура поможет отличить пусковую обмотку от рабочей, если шильдика нет.
Рабочая и пусковая обмотки в однофазном двигателе
Сопротивление обмоток. Начнем с основ
Прежде чем говорить о сопротивлении обмоток статора в однофазном двигателе, нужно иметь понятие о сопротивлении в общем.
Электросопротивление, понятие проводимости
Все тела, пропускающие через себя электроток, могут оказывать этому току некое сопротивление. Свойственное проводникам препятствование тому, чтобы через них проходил ток, и получил название электросопротивления.
Сопротивление металла электричеству объясняется электронной теорией. Двигаясь по проводнику, электроны постоянно встречаются с атомами и остальными электронами. Их взаимодействие между собой приводит к потере некоторого количества энергии со стороны электронов. Они буквально сопротивляются своему движению. Величина сопротивления разных проводников будет разной. Все зависит от их атомного строения.
Таким же образом можно объяснить и сопротивление электрическому току, которое оказывают жидкости и газы. Разница лишь в том, что таких материалах и веществах его оказывают не электроны, а частицы молекул, имеющие определенный заряд.
В вычислениях сопротивление принято обозначать с помощью букв R (r).
Единицей измерения электросопротивления в Международной системе единиц является Ом.
Ом – это сопротивление столба из ртути длиной 106, 3 см и сечением 1 мм2 (при условии, что температура составляет 0° С).
Допустим, сопротивление, оказываемое проводником, равна 4 Ом. Записать это нужно следующим образом: R = 4 Ом; r = 4 Ом.
Чтобы измерять большие электросопротивления, существует официальная единица мегаом. 1 мегаом = 1000 000 Ом.
Чем больше величина электросопротивления конкретного проводника, тем хуже через него проходит электроток. Это правило действует и в обратную сторону. Чем меньше проводник «сопротивляется», тем легче току через него проходить.
Измерение проводимости раствора
Из этого можно сделать логичный вывод: со стороны возможности тока проходить через материал, рассматривают две взаимосвязанные величины: электросопротивление и электропроводность.
Электропроводность говорит о способности вещества или материала к пропусканию тока через себя.
Электропроводность – это обратное значение электросопротивления. Следовательно, выразить ее можно как 1/R. Обозначают ее, как правило, с помощью буквы g.
Что влияет на величину сопротивления, которое выдает проводник: коротко о материале, размерах и температуре
Как мы уже выяснили, величина сопротивления того или иного проводника по большей части зависит от того, из какого материала он сделан. Чтобы охарактеризовать электрическое сопротивление разных веществ, ученые ввели в оборот понятие удельного сопротивления.
Удельное сопротивление – электросопротивление, оказываемое проводником, длина которого 1 м, а площадь поперечного сечения = 1 мм2. Обозначают величину с помощью греческой буквы р. Все материалы, из которых делают проводники, имеют свое удельное сопротивление.
Длина электропроводника имеет непосредственное влияние на его результат его электросопротивления. Высокое сопротивление – высокий показатель. И наоборот.
Обратную пропорциональность сопротивление имеет с площадью поперечного сечения проводника. Толстый проводник будет обладать более низким сопротивлением, чем тонкий, сделанный из того же материала.
Для лучшего понимания данной зависимости можно представить две пары сосудов, которые сообщены между собой. Только вот одна пара имеет тонкую соединяющую их трубку, а другая – толстую. Если обе системы будут заполняться водой, при каких условиях она быстрее перейдет во второй сосуд? Верно, в тех, где трубка толще. Ведь объемная трубка не так сопротивляется воде, как узкая.
По такому же принципу электрический ток легче и быстрее проходит через толстый проводник, ведь он окажет меньшее сопротивление.
Как посчитать сопротивление конкретного проводника? Для этого вам нужно узнать его удельное сопротивление (р), его точную длину в метрах (l) и площадь поперечного сечения (S). Получим:
R = p l / S.
Если ваш проводник имеет круглую форму, площадь его поперечного сечения считают с помощью числа Пи (оно равно 3,14) и диаметра самого проводника (d):
S = Пи х d2 / 4
Длину проводника можно определить, используя площадь поперечного сечения, сопротивление и удельное сопротивление:
l = S R / p.
С помощью данной формулы можно узнать все основные характеристики любого проводника. Для этого нужно, чтобы все остальные величины из формулы были известны.
Если нужно найти площадь сечения, формула выглядит так:
S = p l / R
А вот есть неизвестным параметром является удельное сопротивление, то искать его нужно следующим образом:
р = R S / l
Последняя формула будет полезна в том случае, если вы знаете остальные ее величины: сопротивление и длину проводника, а вот материал нужно найти, ведь определить невооруженным глазом его иногда очень сложно. Полученный результат нужно найти в специальной таблице, которая содержит данные об удельном сопротивлении всех проводников.
Последнее, но не менее важное условие измерения электрического сопротивления – температура воздуха окружающей среды.
Ученые давно выяснили, что повышение температуры воздуха, при котором измеряется сопротивление проводника, связано с повышением его сопротивления. Естественно, с понижением температуры, снижается и величина сопротивления. От материала проводника это явление почти не зависит: при изменении температуры на 1°C, сопротивление изменяется на 0,4%. Значение усредненное и верное только для тех проводников, которые сделаны из чистого металла.
Нужно отметить, что для жидкостей и угля такое правило не работает, зависимость тут обратная: увеличение сопротивления происходит с уменьшением температуры воздуха вокруг.
Электронная теория имеет объяснение и такому явлению. Звучит оно следующим образом: нагреваясь, проводник получает такую тепловую энергию, которая, в конце-концов, поступает ко всем атомам вещества. Результат этого нагревания – более интенсивное движение этих самых атомов. Возрастание движения атомов, в свою очередь, становится причиной большего сопротивления направленному движению свободных электронов. Вместе с этим растет и показатель сопротивления проводника в целом. А вот при понижении температуры условия движения свободных электронов улучшаются, а значит, падает и величина сопротивления.
Сверхпроводимость
Этим можно объяснить еще более интересную возможность проводников – сверхпроводимость.
Сверхпроводимости материалов (т. е. сопротивление которых равно нулю) можно добиться при снижении температуры до абсолютного нуля (нуль по Кельвину) – -273° C. При такой температуре все застывает, в том числе и атомы проводников. Это значит, что препятствовать движению электротока ничего не сможет.
Измерение сопротивления обмотки электроприводов
Электрические двигатели, производимые сегодня, отличаются своей высокой надежностью. Они могут работать десятилетиями, если их грамотно и вовремя обслуживать. В понятие обслуживания однофазного двигателя входит смазка подшипников, их своевременная замена, а также контроль за состоянием обеих обмоток статора.
Зачем проверять сопротивление обмоток в электроприводе
Измерять сопротивление обмоток необходимо, даже если двигатель долгое время стоял без дела. Любые изменения в температурном режиме или влажности помещения могут оказывать влияние на изменчивые свойства машины. Сопротивление может снизиться под влиянием влаги, так что перед подключением мотора к сети обязательно нужна проверка сопротивления обмотки.
Существуют правила технической эксплуатации электрических установок потребителей, которые требуют проведения замеров сопротивления перед включением прибора после ремонта (текущего или капитального), а еще во время плановых испытаний. Они должны проводиться каждые три года.
Сопротивление после любого из ремонтов также помогает понять, насколько качественно была выполнена работа.
Приборы, которыми измеряют сопротивление
Для начала скажем о том, что измерение величины сопротивления всех обмоток проводят относительно корпуса и между самими обмотками.
Механический мегаомметр
Чтобы измерить сопротивление обмоток в статоре однофазного двигателя относительно корпуса используют мегаомметр. Этот прибор позволяет получить наиболее точные результаты, он удобен и компактен. Состоит мегаомметр из собственно омметра и генератора постоянного электротока (он магнитоэлектрический).
Чтобы проверить сопротивление между обмотками, достаточно использовать мультиметр. Вот алгоритм проверки:
- Сначала проверьте, нет ли замыкания на корпус. Помните, что значения на мультиметре всегда приблизительные.
- Переведите мультиметр в режим омметра, установите максимальные значения измерений.
- Один щуп присоедините к корпусу двигателя. Если контакт есть, то можно присоединять и второй. Следите за показаниями.
- Если не заметили сбоев, коснитесь одним из щупов вывода фаз.
- Если изоляция качественная, вы увидите очень высокий показатель на экране. Значение сопротивления может доходить до тысяч мегаом.
Если сопротивление обмоток измеряется в электродвигателе, номинально напряжение которого равно 3000 В (или меньше), нужно использовать мегаомметр, напряжение которого 1000 В. А если номинальное напряжение машины больше 3000 В, то понадобиться тестер, способный выдерживать напряжение 2500 В.
Фазосдвигающий элемент однофазного асинхронного двигателя нужно обязательно отключить от обмотки перед началом их обследования.
Работа и устройство однофазного асинхронного двигателя
Двигатель имеет две фазы, однако работает лишь одна из них. Поэтому его и называют однофазным. Как и любая другая подобная машина, однофазный движок состоит из двух основных частей: статора (статичен) и ротора (подвижен). Их основа – электротехническая сталь. Это асинхронная машина, в которой неподвижная основная обмотка лишь одна (работающая или главная). Она и подключена к источнику переменного тока. Важнейшее преимущество такого электродвигателя – простота строения: ротор представляет замкнутая обмотка по типу беличья клетка. Главный минус – низкое значение пускового момента и коэффициента полезного действия (КПД).
Вращающееся магнитное поле
А вот главным минусом однофазного тока является тот факт, что он не может генерировать вращающееся магнитное поле. Поэтому однофазный двигатель никогда не начнет работу самостоятельно, даже если включить его в сеть.
Для возникновения магнитного поля, которое сможет запустить ротор в работу, статор однофазного двигателя должен быть оборудован двумя обмотками. А еще она должна быть перпендикулярно смещена рабочей фазе.
Чтобы осуществить такой сдвиг важно использовать фазосдвигающие элементы. Ими могут послужить резистор или катушка индукции, но наилучшие показатели двигатель будет выдавать, если в цепь включен конденсатор.
Есть, так называемые, конденсаторные электродвигатели. В них работают обе катушки на протяжении всей работы мотора. Пусковая (вспомогательная) обмотка в них подключена через конденсатор. Их называть однофазными не совсем корректно.
Как происходит запуск
В обмотке подвижной части двигателя индукционный ток может возникать только в том случае, когда силовые линии поля пересекают витки. А для этого скорость вращения поля должна быть немного меньше скорости вращения витков.
Это и стало причиной, по которой двигатель назвали асинхронным.
С увеличением нагрузки на мотор, снижается скорость вращения и повышается его механическая мощность.
По какому принципу работает
- Ток порождает импульсное магнитное поле в статичной части двигателя. Магнитное поле можно рассматривать как два отдельный с одинаковыми амплитудами и частотами.
- Если ротор неподвижен, появляющиеся из-за действия поля моменты равных нулю, хоть и разнонаправленны.
- Если ротор начал движение, соответствующий момент начнет преобладать. Это не даст элементу двигаться в другую сторону.
- Если необходимые механизмы для запуска ротора отсутствуют, запуститься он не сможет, что приводит к возникновению нулевых моментов.
Пуск выполняет магнитное поле, сформированное благодаря присутствию в статоре двух обмоток: рабочей и пусковой. Объем пусковой меньше, чем рабочей. Дополнительная обмотка подключена к сети, как правило, через емкость. Включается она только на момент запуска двигателя. Если мотор обладает небольшой мощностью, пусковая фаза в нем наверняка замкнута накоротко.
Пусковой нажим
Запускает мотор кнопка, которую нужно удерживать 2-3 секунды. В это время двигатель разгоняется до своей нормальной скорости. Когда клавиша отпускается, отключается пусковая обмотка. Двигатель переходит в однофазный режим работы.
Если нажать пусковую кнопку больше, чем на три секунды, изоляция обмотки может перегреться или даже загореться. Это, конечно, приведет к поломке агрегата, а пожар может нести угрозу здоровью и жизни людей. Более продолжительное время пребывания под нагрузкой может послужить причиной к перегреву, возгоранию изоляции и неисправности приспособления.
Для увеличения надежности машины в ее корпус монтируют центробежный выключатель и тепловое реле. Первый механизм нужен для автоматического отключения пусковой обмотки, когда ротор наберет нужную скорость. Второй механизм служит для отключения перегревшихся обмоток.
Механизм работы
Чтобы устройство нормально работало, его необходимо подключить к однофазной сети с напряжением в 220В. То есть, розетки в любой квартире будет достаточно. Поэтому он и получил такое распространение. Однофазный двигатель стоит буквально во всех наших бытовых электроприборах.
Все электродвигатели такого типа можно поделить на еще два подтипа:
- В первом случае вспомогательная обмотка работает через пусковой конденсатор только в момент запуска привода. Когда агрегат набирает нужную скорость вращения, она выключается.
- Второй подвид машин содержит рабочий конденсатор, об этом упоминалось выше. В этой ситуации пусковая обмотка продолжает работу вместе с запустившимся двигателем.
Конденсатор тоже требует проверки сопротивления. Осуществить процедуру можно мультиметром.
Проверка конденсатора мультиметром
Электронный мегаомметр
Понятное дело, что при проверке сопротивления омметру нет равных. Он дает наиболее точные результаты измерения. Это позволяет оценивать целостность диэлектрика. Ведь работоспособность машины зависит от него не меньше, чем от исправности обмоток.
Если вы занимаетесь проверкой дома, точные значения вам ни к чему. Тут главное найти (или не найти) поломку. Мультиметр с этим справляется отлично.
Замеры проводят так:
- мультиметр включают в режим омметра;
- выставляют максимальное значение – бесконечное;
- измеряют величину сопротивления емкости на выводах.
Работа мультиметра в режиме омметра
Возможны следующие результаты:
- Сопротивление меньше бесконечности. Прибор неисправен. Возможно вытек электролит или сломан диэлектрик.
- Сначала заметно небольшое отклонение стрелки, но она вернулась на место. Конденсатор функционирует исправно.
- Стрелка тестера зафиксировалась на одном из значений. Это также говорит о наличии поломки в приборе.
Любой привод можно снять с одного электромотора и подключить к другому. Как пример, двигатель с холодильника (если он исправен) будет отлично функционировать в газонокосилке.
Схема для подключения
Всего существует три схемы, по которым можно подключить однофазный асинхронный двигатель с конденсатором:
- Пусковая обмотка работает через конденсатор, но выключается, когда ротор набирает нормальную скорость.
- Вспомогательная обмотка работает вначале, но подключается через сопротивление.
- Вспомогательная обмотка работает через конденсатор на протяжении всей работы электродвигателя.
Как определить рабочую и пусковую обмотки, измерив сопротивление их выводов
Чтобы измерить величину сопротивления обмоток в однофазном двигателе вам нужен мультиметр, включенный в режиме измерения Ом (омметра).
Провода, выглядывающие из электропривода (любую пару) соединяем с щупами на мультиметре, меряем значение.
Если видите на экране цифру один, повторите измерение с любым другим концом.
Запишите величину сопротивления, которое показала выбранная вами пара. Затем щупы мультиметра (все еще в режиме омметра) цепляйте к двум другим выводам, то есть ко второй паре проводов, произведите замер.
Полученные данные тоже обязательно запишите и сравните с первым результатом.
Сопротивление исправной рабочей обмотки всегда будет показывать меньшее значение, чем у вспомогательной. Допустим, вторая пара проводов, показала сопротивление больше. Тогда можно смело утверждать, что первая пара проводов говорит о принадлежности к рабочей обмотке, а вторая, соответственно, к пусковой. И наоборот.
Обозначьте обе обмотки, чтобы впоследствии, когда снова нужен будет ремонт или обычная проверка, не пришлось проделывать все это снова.
Маркировать концы проводов (выводы) можно по современным стандартам:
- знаками U1-U2 помечают главную обмотку;
- знаками B1-B2 помечают вспомогательную обмотку.
Такие обозначения ставятся в тех случаях, когда из двигателя видно четыре вывода, как в вышеописанной ситуации. Однако, на вашем пути может встретиться двигатель, с тремя выводами. Что вы должны делать в такой ситуации?
Итак, замеры каждого из вывода будут приблизительно такими: 10 Ом, 25 Ом и 15 Ом. После того как завершите эти измерения найдите тот вывод, который с двумя другими выводами покажет 10 и 15 Ом. Это провод от рабочей обмотки. Вывод, показывающий сопротивление 10 Ом тоже главный, а тот, что дал результат 15 Ом – пусковой. Он должен быть соединен со вторым главным с помощью конденсатора.
Иногда первоначальные измерения могут показать 10 Ом, 10 Ом и 20 Ом. Это норма, такие обмотки тоже существуют, их тоже ставят на самые разные бытовые электроприборы. Особенность такого двигателя заключается в том, что какая конкретно обмотка будет выполнять роль вспомогательной, а какая главной абсолютно не важно. Просто одну из них (с ролью вспомогательной) подключают через конденсатор.
Подведем итог
Сопротивление обмоток – важнейший фактор в работе с электродвигателями. Его своевременное измерение (трижды в год и сразу после ремонта), наряду с остальным техобслуживанием, помогает продолжить работу асинхронной однофазной машины.
С помощью мультиметра, работающего в режиме измерения Ом, можно быстро определить, какая обмотка рабочая, а какая пусковая.
Сопротивление также помогает проверить работоспособность и конденсатора, и обмоток.