Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
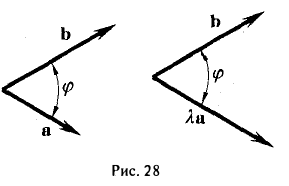
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Линейная алгебра для разработчиков игр
Эта статья является переводом цикла из четырёх статей «Linear algebra for game developers», написанных David Rosen и посвящённых линейной алгебре и её применению в разработке игр. С оригинальными статьями можно ознакомиться тут: часть 1, часть 2, часть 3 и часть 4. Я не стал публиковать переводы отдельными топиками, а объединил все статьи в одну. Думаю, что так будет удобнее воспринимать материал и работать с ним. Итак приступим.
Зачем нам линейная алгебра?
Одним из направлений в линейной алгебре является изучение векторов. Если в вашей игре применяется позиционирование экранных кнопок, работа с камерой и её направлением, скоростями объектов, то вам придётся иметь дело с векторами. Чем лучше вы понимаете линейную алгебру, тем больший контроль вы получаете над поведением векторов и, следовательно, над вашей игрой.
Что такое вектор?
В играх вектора используются для хранения местоположений, направлений и скоростей. Ниже приведён пример двухмерного вектора: 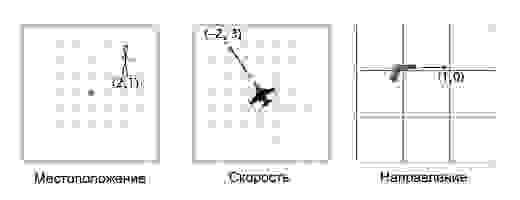
Вектор местоположения (также называемый «радиус-вектором») показывает, что человек стоит в двух метрах восточнее и в одном метре к северу от исходной точки. Вектор скорости показывает, что за единицу времени самолёт перемещается на три километра вверх и на два — влево. Вектор направления говорит нам о том, что пистолет направлен вправо.
Как вы можете заметить, вектор сам по себе всего лишь набор цифр, который обретает тот или иной смысл в зависимости от контекста. К примеру, вектор (1, 0) может быть как направлением для оружия, как показано на картинке, так и координатами строения в одну милю к востоку от вашей текущей позиции. Или скоростью улитки, которая двигается вправо со скоростью в 1 милю в час (прим. переводчика: довольно быстро для улитки, 44 сантиметра в секунду).
Важно отслеживать единицы измерения. Допустим у нас есть вектор V (3,5,2). Это мало что говорит нам. Три чего, пять чего? В нашей игре Overgrowth расстояния указываются в метрах, а скорости в метрах в секунду. Первое число в этом векторе — это направление на восток, второе — направление вверх, третье — направление на север. Отрицательные числа обозначают противоположные направления, на запад, вниз и на юг. Местоположение, определяемое вектором V (3,5,2), находится в трёх метрах к востоку, в пяти метрах вверху и в двух метрах к северу, как показано на картинке ниже.
Итак, мы изучили основы работы с векторами. Теперь узнаем как вектора использовать.
Сложение векторов
Чтобы сложить вектора, нам надо просто сложить каждую их составляющую друг с другом. Например:
(0, 1, 4) + (3, -2, 5) = (0+3, 1-2, 4+5) = (3, -1, 9)
Зачем нам нужно складывать вектора? Наиболее часто сложение векторов в играх применяется для физического интегрирования. Любой физический объект будет иметь вектора для местоположения, скорости и ускорения. Для каждого кадра (обычно это одна шестидесятая часть секунды), мы должны интегрировать два вектора: добавить скорость к местоположению и ускорение к скорости.
Давайте рассмотрим пример с прыжками Марио. Он начинает с позиции (0, 0). В момент начала прыжка его скорость (1, 3), он быстро двигается вверх и вправо. Его ускорение равно (0, -1), так как гравитация тянет его вниз. На картинке показано, как выглядит его прыжок, разбитый на семь кадров. Чёрным текстом показана его скорость в каждом фрейме.
Давайте рассмотрим первые кадры поподробнее, чтобы понять как всё происходит.
Для первого кадра, мы добавляем скорость Марио (1, 3) к его местоположению (0, 0) и получаем его новые координаты (1, 3). Затем мы складываем ускорение (0, -1) с его скоростью (1, 3) и получаем новое значение скорости Марио (1, 2).
Делаем то-же самое для второго кадра. Добавляем скорость (1, 2) к местоположению (1, 3) и получаем координаты (2, 5). Затем добавляем ускорение (0, -1) к его скорости (1, 2) и получаем новую скорость (1, 1).
Обычно игрок контролирует ускорение игрового персонажа с помощью клавиатуры или геймпада, а игра, в свою очередь, рассчитывает новые значения для скоростей и местоположения, используя физическое сложение (через сложение векторов). Это та-же задача, которая решается в интегральном исчислении, просто мы его сильно упрощаем для нашей игры. Я заметил, что мне намного проще внимательно слушать лекции по интегральному исчислению, думая о практическом его применении, которое мы только что описали.
Вычитание векторов
Вычитание рассчитывается по тому-же принципу что и сложение — вычитаем соответствующие компоненты векторов. Вычитание векторов удобно для получения вектора, который показывает из одного местоположения на другое. Например, пусть игрок находится по координатам (1, 2) с лазерным ружьём, а вражеский робот находится по координатам (4, 3). Чтобы определить вектор движения лазерного луча, который поразит робота, нам надо вычесть местоположение игрока из местоположения робота. Получаем:
(4, 3) — (1, 2) = (4-1, 3-2) = (3, 1).
Умножение вектора на скаляр
Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например (3, 4) — вектор, а 5 — это скаляр. В играх, часто бывает нужно умножить вектор на число (скаляр). Например, моделируя простое сопротивление воздуха путём умножения скорости игрока на 0.9 в каждом кадре. Чтобы сделать это, нам надо умножить каждый компонент вектора на скаляр. Если скорость игрока (10, 20), то новая скорость будет:
0.9*(10, 20) = (0.9 * 10, 0.9 * 20) = (9, 18).
Длина вектора
Если у нас есть корабль с вектором скорости V (4, 3), нам также понадобится узнать как быстро он двигается, чтобы посчитать потребность в экранном пространстве или сколько потребуется топлива. Чтобы сделать это, нам понадобится найти длину (модуль) вектора V. Длина вектора обозначается вертикальными линиями, в нашем случае длина вектора V будет обозначаться как |V|.
Мы можем представить V как прямоугольный треугольник со сторонами 4 и 3 и, применяя теорему Пифагора, получить гипотенузу из выражения: x 2 + y 2 = h 2
В нашем случае — длину вектора H с компонентами (x, y) мы получаем из квадратного корня: sqrt(x 2 + y 2 ).
Итак, скорость нашего корабля равна:
|V| = sqrt(4 2 + 3 2 ) = sqrt(25) = 5
Этот подход используется и для трёхмерных векторов. Длина вектора с компонентами (x, y, z) рассчитывается как sqrt(x 2 + y 2 + z 2 )
Расстояние
Если игрок P находится в точке (3, 3), а взрыв произошёл в точке E по координатам (1, 2), нам надо определить расстояние между игроком и взрывом, чтобы рассчитать степень ущерба, нанесённого игроку. Это легко сделать, комбинируя две вышеописанных операции: вычитание векторов и их длину.
Мы вычитаем P — E, чтобы получить вектор между ними. А затем определяем длину этого вектора, что и даёт нам искомое расстояние. Порядок следования операндов тут не имеет значения, |E — P| даст тот-же самый результат.
Расстояние = |P — E| = |(3, 3) — (1, 2)| = |(2, 1)| = sqrt(2 2 +1 2 ) = sqrt(5) = 2.23
Нормализация
Когда мы имеем дело с направлениями (в отличие от местоположений и скоростей), важно, чтобы вектор направления имел длину, равную единице. Это сильно упрощает нам жизнь. Например, допустим орудие развёрнуто в направлении (1, 0) и выстреливает снаряд со скоростью 20 метров в секунду. Каков в данном случае вектор скорости для выпущенного снаряда?
Так как вектор направления имеет длину равную единице, мы умножаем направление на скорость снаряда и получаем вектор скорости (20, 0). Если-же вектор направления имеет отличную от единицы длину, мы не сможем сделать этого. Снаряд будет либо слишком быстрым, либо слишком медленным.
Вектор с длиной равной единице называется «нормализованным». Как сделать вектор нормализованным? Довольно просто. Мы делим каждый компонент вектора на его длину. Если, к примеру, мы хотим нормализовать вектор V с компонентами (3, 4), мы просто делим каждый компонент на его длину, то есть на 5, и получаем (3/5, 4/5). Теперь, с помощью теоремы Пифагора, мы убедимся в том, что его длина равна единице:
(3/5) 2 + (4/5) 2 = 9/25 + 16/25 = 25/25 = 1
Скалярное произведение векторов
Что такое скалярное произведение (записывается как •)? Чтобы рассчитать скалярное произведение двух векторов, мы должны умножить их компоненты, а затем сложить полученные результаты вместе
(a1, a2) • (b1, b2) = a1b1 + a2b2
Например: (3, 2) • (1, 4) = 3*1 + 2*4 = 11. На первый взгляд это кажется бесполезным, но посмотрим внимательнее на это:
Здесь мы можем увидеть, что если вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля.
В основном, с помощью скалярного произведения векторов можно рассчитать, сколько их указывает в одном направлении. И хоть это лишь малая часть возможностей скалярного произведения, но уже очень для нас полезная.
Допустим у нас есть стражник, расположенный в G(1, 3) смотрящий в направлении D(1,1), с углом обзора 180 градусов. Главный герой игры подсматривает за ним с позиции H(3, 2). Как определить, находится-ли главный герой в поле зрения стражника или нет? Сделаем это путём скалярного произведения векторов D и V (вектора, направленного от стражника к главному герою). Мы получим следующее:
V = H — G = (3, 2) — (1, 3) = (3-1, 2-3) = (2, -1)
D•V = (1, 1) • (2, -1) = 1*2 + 1*-1 = 2-1 = 1
Так как единица больше нуля, то главный герой находится в поле зрения стражника.
Мы уже знаем, что скалярное произведение имеет отношение к определению направления векторов. А каково его более точное определение? Математическое выражение скалярного произведения векторов выглядит так:
Где Θ (произносится как «theta») — угол между векторами A и B.
Это позволяет нам найти Θ (угол) с помощью выражения:
Как я говорил ранее, нормализация векторов упрощает нашу жизнь. И если A и B нормализованы, то выражение упрощается следующим образом:
Давайте опять рассмотрим сценарий со стражником. Пусть теперь угол обзора стражника будет равен 120 градусам. Получим нормализованные вектора для направления взгляда стражника (D’) и для направления от стражника к главному герою (V’). Затем определим угол между ними. Если угол более 60 градусов (половина от угла обзора), то главный герой находится вне поля зрения стражника.
D’ = D / |D| = (1, 1) / sqrt(1 2 + 1 2 ) = (1, 1) / sqrt(2) = (0.71, 0.71)
V’ = V / |V| = (2, -1) / sqrt(2 2 + (-1) 2 ) = (2,-1) / sqrt(5) = (0.89, -0.45)
Θ = acos(D’V’) = acos(0.71*0.89 + 0.71*(-0.45)) = acos(0.31) = 72
Угол между центром поля зрения стражника и местоположением главного героя составляет 72 градуса, следовательно стражник его не видит.
Понимаю, что это выглядит довольно сложно, но это потому, что мы всё делаем вручную. В программе это всё довольно просто. Ниже показано как я сделал это в нашей игре Overgrowth с помощью написанных мной С++ библиотек для работы с векторами:
Векторное произведение
Допустим у нас есть корабль с пушками, которые стреляют в правую и в левую стороны по курсу. Допустим, что лодка расположена вдоль вектора направления (2, 1). В каких направлениях теперь стреляют пушки?
Это довольно просто в двухмерной графике. Чтобы повернуть направление на 90 градусов по часовой стрелке, достаточно поменять местами компоненты вектора, а затем поменять знак второму компоненту.
(a, b) превращается в (b, -a). Следовательно у корабля, расположенного вдоль вектора (2, 1), пушки справа по борту будут стрелять в направлении (1, -2), а пушки с левого борта, будут стрелять в противоположном направлении. Меняем знаки у компонент вектора и получаем (-1, 2).
А что если мы хотим рассчитать это всё для трехмерной графики? Рассмотрим пример с кораблём.
У нас есть вектор мачты M, направленной прямо вверх (0, 1, 0) и направление ветра: север-северо-восток W (1, 0, 2). И мы хотим вычислить вектор направления паруса S, чтобы наилучшим образом «поймать ветер».
Для решения этой задачи мы используем векторное произведение: S = M x W.
Подставим теперь нужные нам значения:
S = MxW = (0, 1, 0) x (1, 0, 2) = ([1*2 — 0*0], [0*1 — 0*2], [0*0 — 1*1]) = (2, 0, -1)
Для расчётов вручную довольно сложно, но для графических и игровых приложений я рекомендую написать функцию, подобную той, что указана ниже и не вдаваться более в детали подобных расчётов.
Векторное произведение часто используется в играх, чтобы рассчитать нормали к поверхностям. Направления, в которых «смотрит» та или иная поверхность. Например, рассмотрим треугольник с векторами вершин A, B и С. Как мы найдем направление в котором «смотрит» треугольник, то есть направление перпендикулярное его плоскости? Это кажется сложным, но у нас есть инструмент для решения этой задачи.
Используем вычитание, для определения направления из A в С (C — A), пусть это будет «грань 1» (Edge 1) и направление из A в B (B — A), пусть это будет «грань 2» (Edge 2). А затем применим векторное произведение, чтобы найти вектор, перпендикулярный им обоим, то есть перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».
Вот так это выглядит в коде:
В играх основное выражение освещённости записывается как N • L, где N — это нормаль к освещаемой поверхности, а L — это нормализованный вектор направления света. В результате поверхность выглядит яркой, когда на неё прямо падает свет, и тёмной, когда этого не происходит.
Теперь перейдем к рассмотрению такого важного для разработчиков игр понятия, как «матрица преобразований» (transformation matrix).
Для начала изучим «строительные блоки» матрицы преобразований.
Базисный вектор
Допустим мы пишем игру Asteroids на очень старом «железе» и нам нужен простой двухмерный космический корабль, который может свободно вращаться в своей плоскости. Модель корабля выглядит так:
Как нам рисовать корабль, когда игрок поворачивает его на произвольный градус, скажем 49 градусов против часовой стрелки. Используя тригонометрию, мы можем написать функцию двухмерного поворота, которая принимает координаты точки и угол поворота, и возвращает координаты смещённой точки:
Применяя эту функцию ко всем трём точкам, мы получим следующую картину:
Операции с синусами и косинусами работают довольно медленно, но так как мы делаем расчёты лишь для трёх точек, это будет нормально работать даже на старом «железе» (прим. переводчика: в случаях, когда предполагается интенсивное использование тригонометрических функций, для ускорения вычислений, в памяти организуют таблицы значений для каждой функции и рассчитывают их во время запуска приложения. Затем при вычислении той или иной тригонометрической функции просто производится обращение к таблице).
Пусть теперь наш корабль выглядит вот так:
Теперь старый подход будет слишком медленным, так как надо будет поворачивать довольно большое количество точек. Одно из элегантных решений данной проблемы будет звучать так — «Что если вместо поворота каждой точки модели корабля, мы повернём координатную решётку нашей модели?»
Как это работает? Давайте посмотрим внимательнее, что собой представляют координаты.
Когда мы говорим о точке с координатами (3, 2), мы говорим, что её местоположение находится в трех шагах от точки отсчёта по координатной оси X, и двух шагах от точки отсчёта по координатной оси Y.
По-умолчанию координатные оси расположены так: вектор координатной оси X (1, 0), вектор координатной оси Y (0, 1). И мы получим расположение: 3(1, 0) + 2(0, 1). Но координатные оси не обязательно должны быть в таком положении. Если мы повернём координатные оси, в это-же время мы повернём все точки в координатной решётке.
Чтобы получить повернутые оси X и Y мы применим тригонометрические функции, о которых говорили выше. Если мы поворачиваем на 49 градусов, то новая координатная ось X будет получена путём поворота вектора (0, 1) на 49 градусов, а новая координатная ось Y будет получена путём поворота вектора (0, 1) на 49 градусов. Итак вектор новой оси X у нас будет равен (0.66, 0.75), а вектор новой оси Y будет (-0.75, 0.66). Сделаем это вручную для нашей простой модели из трёх точек, чтобы убедиться, что это работает так, как нужно:
Координаты верхней точки (0, 2), что означает, что её новое местоположение находится в 0 на новой (повёрнутой) оси X и 2 на новой оси Y:
0*(0.66,0.75) + 2*(-0.75, 0.66) = (-1.5, 1.3)
Нижняя левая точка (-1, -1), что означает, что её новое местоположение находится в -1 на повернутой оси X, и -1 на повернутой оси Y:
-1*(0.66,0.75) + -1*(-0.75, 0.66) = (0.1, -1.4)
Нижняя правая точка (1, -1), что означает её новое местоположение находится в 1 на повернутой оси X, и -1 на повернутой оси Y
1*(0.66,0.75) + -1*(-0.75, 0.66) = (1.4, 0.1)
Мы показали, как координаты корабля отображаются в другой координатной сетке с повернутыми осями (или «базисными векторами»). Это удобно в нашем случае, так как избавляет нас от необходимости применять тригонометрические преобразования к каждой из точек модели корабля.
Каждый раз, когда мы изменяем базисные вектора (1, 0) и (0, 1) на (a, b) и (c, d), то новая координата точки (x, y) может быть найдена с помощью выражения:
Обычно базисные вектора равны (1, 0) и (0, 1) и мы просто получаем x(1, 0) + y(0, 1) = (x, y), и нет необходимости заботиться об этом дальше. Однако, важно помнить, что мы можем использовать и другие базисные вектора, когда нам это нужно.
Матрицы
Матрицы похожи на двухмерные вектора. Например, типичная 2×2 матрица, может выглядеть так:
Когда вы умножаете матрицу на вектор, вы суммируете скалярное произведение каждой строки с вектором, на который происходит умножение. Например, если мы умножаем вышеприведённую матрицу на вектор (x, y), то мы получаем:
Будучи записанным по-другому, это выражение выглядит так:
Выглядит знакомо, не так-ли? Это в точности такое-же выражение, которые мы использовали для смены базисных векторов. Это означает, что умножая 2×2 матрицу на двухмерный вектор, мы тем самым меняем базисные вектора. Например, если мы вставим стандартные базисные вектора в (1, 0) и (0, 1) в колонки матрицы, то мы получим:
Это единичная матрица, которая не даёт эффекта, который мы можем ожидать от нейтральных базисных векторов, которые мы указали. Если-же мы повернём базисные вектора на 49-градусов, то мы получим:
Эта матрица будет поворачивать двухмерный вектор на 49 градусов против часовой стрелки. Мы можем сделать код нашей игры Asteriods более элегантным, используя матрицы вроде этой. Например, функция поворота нашего корабля может выглядеть так:
Однако, наш код будет ещё более элегантным, если мы сможем также включить в эту матрицу перемещение корабля в пространстве. Тогда у нас будет единая структура данных, которая будет заключать в себе и применять информацию об ориентации объекта и его местоположении в пространстве.
К счастью есть способ добиться этого, хоть это и выглядит не очень элегантно. Если мы хотим переместиться с помощью вектора (e, f), мы лишь включаем его в нашу матрицу преобразования:
И добавляем дополнительную единицу в конец каждого вектора, определяющего местоположение объекта, например так:
Теперь, когда мы перемножаем их, мы получаем:
(a, c, e) • (x, y, 1) + (b, d, f) • (x, y, 1) + (0, 0, 1) • (x, y, 1)
Что, в свою очередь, может быть записано как:
x(a, b) + y(c, d) + (e, f)
Теперь у нас есть полный механизм трансформации, заключённый в одной матрице. Это важно, если не принимать в расчёт элегантность кода, так как с ней мы теперь можем использовать все стандартные манипуляции с матрицами. Например перемножить матрицы, чтобы добавить нужный эффект, или мы можем инвертировать матрицу, чтобы получить прямо противоположное положение объекта.
Трехмерные матрицы
Матрицы в трехмерном пространстве работают так-же как и в двухмерном. Я приводил примеры с двухмерными векторами и матрицами, так как их просто отобразить с помощью дисплея, показывающего двухмерную картинку. Нам просто надо определить три колонки для базисных векторов, вместо двух. Если базисные вектора это (a,b,c), (d,e,f) and (g,h,i) то наша матрица будет выглядеть так:
Если нам нужно перемещение (j,k,l), то мы добавляем дополнительную колонку и строку, как говорили раньше:
И добавляем единицу [1] в вектор, как здесь:
Вращение в двухмерном пространстве
Так как в нашем случае у нас только одна ось вращения (расположенная на дисплее), единственное, что нам надо знать, это угол. Я говорил об этом ранее, упоминая, что мы можем применять тригонометрические функции для реализации функции двухмерного вращения наподобие этой:
Более элегантно это можно выразить в матричной форме. Чтобы определить матрицу, мы можем применить эту функцию к осям (1, 0) и (0, 1) для угла Θ, а затем включить полученные оси в колонки нашей матрицы. Итак, начнём с координатной оси X (1, 0). Если мы применим к ней нашу функцию, мы получим:
(1*cos(Θ) — 0*sin(Θ), 1*sin(Θ) + 0*cos(Θ)) = (cos(Θ), sin(Θ))
Затем, мы включаем координатную ось Y (0, 1). Получим:
(0*cos(Θ) — 1*sin(Θ), 0*sin(Θ) + 1*cos(Θ)) = (-sin(Θ), cos(Θ))
Включаем полученные координатные оси в матрицу, и получаем двухмерную матрицу вращения:
Применим эту матрицу к Сюзанне, мартышке из графического пакета Blender. Угол поворота Θ равен 45 градусов по часовой стрелке.
Как видите — это работает. Но что если нам надо осуществить вращение вокруг точки, отличной от (0, 0)?
Например, мы хотим вращать голову мартышки вокруг точки, расположенной в её ухе:
Чтобы сделать это, мы можем начать с создания матрицы перемещения (translation matrix) T, которая перемещает объект из начальной точки в точку вращения в ухе мартышки, и матрицу вращения R, для вращения объекта вокруг начальной точки. Теперь для вращения вокруг точки, расположенной в ухе, мы можем сперва переместить точку в ухе на место начальной точки, с помощью инвертирования матрицы T, записанной как T -1 . Затем, мы вращаем объект вокруг начальной точки, с помощью матрицы R, а затем применяем матрицу T для перемещения точки вращения назад, к своему исходному положению.
Ниже дана иллюстрация к каждому из описанных шагов:
Это важный шаблон, который мы будем применять позднее — применение вращения для двух противоположных трансформаций позволяет нам вращать объект в другом «пространстве». Что очень удобно и полезно.
Теперь рассмотрим трёхмерное вращение.
Трёхмерное вращение
Вращение вокруг оси Z работает по тому-же принципу, что и вращение в двухмерном пространстве. Нам лишь нужно изменить нашу старую матрицу, добавив к ней дополнительную колонку и строку:
Применим эту матрицу к трехмерной версии Сюзанны, мартышки из пакета Blender. Угол поворота Θ пусть будет равен 45 градусов по часовой стрелке.
То-же самое. Вращение только вокруг оси Z ограничивает нас, как насчёт вращения вокруг произвольной оси?
Вращение, определяемое осью и углом (Axis-angle rotation)
Представление вращения, определяемого осью и углом, также известно как вращение в экспоненциальных координатах, параметризованное вращением двух величин. Вектора, определяющего вращение направляющей оси (прямая линия) и угла, описывающего величину поворота вокруг этой оси. Вращение осуществляется согласно правилу правой руки.
Итак, вращение задаётся двумя параметрами (axis, angle), где axis — вектор оси вращения, а angle — угол вращения. Этот приём довольно прост и являет собой отправную точку для множества других операций вращения, с которыми я работаю. Как практически применить вращение, определяемое осью и углом?
Допустим мы имеем дело с осью вращения, показанной на рисунке ниже:
Мы знаем как вращать объект вокруг оси Z, и мы знаем как вращать объект в других пространствах. Итак, нам лишь надо создать пространство, где наша ось вращения будет являться осью Z. И если эта ось будет осью Z, то что будет являться осями X и Y? Займемся вычислениями сейчас.
Чтобы создать новые оси X и Y нам нужно лишь выбрать два вектора, которые перпендикулярны новой оси Z и перпендикулярны друг другу. Мы уже говорили ранее о векторном умножении, которое берёт два вектора и даёт в итоге перпендикулярный им вектор.
У нас есть один вектор сейчас, это ось вращения, назовём его A. Возьмём теперь случайный другой вектор B, который находится не в том-же направлении, что и вектор A. Пусть это будет (0, 0, 1) к примеру.
Теперь мы имеем ось вращения A и случайный вектор B, мы можем получить нормаль C, через векторное произведение A и B. С перпендикулярен векторам A и B. Теперь мы делаем вектор B перпендикулярным векторам A и C через их векторное произведение. И всё, у нас есть все нужные нам оси координат.
На словах это звучит сложно, но довольно просто выглядит в коде или будучи показанным в картинках.
Ниже показано, как это выглядит в коде:
Тут показана иллюстрация для каждого шага:
Теперь, имея информацию о новых координатных осях, мы можем составить матрицу M, включив каждую ось как колонку в эту матрицу. Нам надо убедиться, что вектор A является третьей колонкой, чтобы он был нашей новой осью координат Z.
Теперь это похоже на то, что мы делали для поворота в двухмерном пространстве. Мы можем применить инвертированную матрицу M, чтобы переместиться в новую систему координат, затем произвести вращение, согласно матрице R, чтобы повернуть объект вокруг оси Z, затем применить матрицу M, чтобы вернуться в исходное координатное пространство.
Теперь мы можем вращать объект вокруг произвольной оси. В конце концов мы можем просто создать матрицу T = T = M -1 RM и использовать её много раз, без дополнительных усилий с нашей стороны. Есть более эффективные способы конвертирования вращений, определяемых осью и углом во вращения, определяемые матрицами. Просто описанный нами подход показывает многое из того, о чём мы говорили ранее.
Вращение, определяемое осью и углом, возможно, самый интуитивно понятный способ. Применяя его, очень легко инвертировать поворот, поменяв знак у угла, и легко интерполировать, путём интерполяции угла. Однако тут есть серьёзное ограничение, и заключается оно в том, что такое вращение не является суммирующим. То есть вы не можете комбинировать два вращения, определяемых осью и углом в третье.
Вращение, определяемое осью и углом — хороший способ для начала, но оно должно быть преобразовано во что-то другое, чтобы использоваться в более сложных случаях.
Эйлеровские углы
Эйлеровские углы представляют собой другой способ вращения, заключающийся в трёх вложенных вращениях относительно осей X, Y и Z. Вы, возможно, сталкивались с их применением в играх, где камера показывает действие от первого лица, либо от третьего лица.
Допустим вы играете в шутер от первого лица и вы повернулись на 30 градусов влево, а затем посмотрели на 40 градусов вверх. В конце-концов в вас стреляют, попадают, и, в результате удара, камера поворачивается вокруг своей оси на 45 градусов. Ниже показано вращение с помощью углов Эйлера (30, 40, 45).
Углы Эйлера — удобное и простое в управлении средство. Но у этого способа есть два недостатка.
Первый, это вероятность возникновения ситуации под названием «блокировка оси» или «шарнирный замок» (gimbal lock). Представьте, что вы играете в шутер от первого лица, где вы можете посмотреть влево, вправо, вверх и вниз или повернуть камеру вокруг зрительной оси. Теперь представьте, что вы смотрите прямо вверх. В этой ситуации попытка взглянуть налево или направо будет аналогична попытке вращения камеры. Всё что мы можем вы этом случае, это вращать камеру вокруг своей оси, либо посмотреть вниз. Как вы можете представить, это ограничение делает непрактичным применение углов Эйлера в лётных симуляторах.
Второе — интерполяция между двумя эйлеровскими углами вращения не даёт кратчайшего пути между ними.
Например, у вас две интерполяции между двумя одинаковыми вращениями. Первая использует интерполяцию эйлеровского угла, вторая использует сферическую линейную интерполяцию (spherical linear interpolation (SLERP)), чтобы найти кратчайший путь.
Итак, что-же больше подойдет для интерполяции вращений? Может быть матрицы?
Вращение с помощью матриц
Как мы уже говорили ранее, матрицы вращения хранят в себе информацию о трёх осях. Это означает, что интерполяция между двумя матрицами лишь линейно интерполирует каждую ось. В результате это даёт нам эффективный путь, то так-же привносит новые проблемы. Например, тут показаны два вращения и одно интерполированное полу-вращение:
Как вы можете заметить, интерполированное вращение значительно меньше, чем любое из исходных вращений, и две оси более не перпендикулярны друг другу. Это логично, если вдуматься — середина отрезка, соединяющего любые две точки на сфере будет расположена ближе к центру сферы.
Это в свою очередь порождает известный «эффект фантика» (candy wrapper effect), при применении скелетной анимации. Ниже показана демонстрация этого эффекта на примере кролика из нашей игры Overgrowth (прим. переводчика: обратите внимание на середину туловища кролика).
Вращение, основанное на матричных операциях, очень полезно, так как они могут аккумулировать вращения без всяких проблем, вроде блокировки оси (gimbal lock), и может очень эффективно применяться к точкам сцены. Вот почему поддержка вращения на матрицах встроена в графические карты. Для любого типа трёхмерной графики матричный формат вращения — это всегда итоговый применяемый способ.
Однако, как мы уже знаем, матрицы не очень хорошо интерполируются, и они не столь интуитивно понятны.
Итак, остался только один главный формат вращения. Последний, но тем не менее, важный.
Кватернионы
Что-же такое кватернионы? Если очень кратко, то это альтернативный вариант вращения, основанный на оси и угле (axis-angle rotation), который существует в пространстве.
Подобно матрицам они могут аккумулировать вращения, то есть вы можете составлять из них цепочку вращений, без опаски получить блокировку оси (gimbal lock). И в то-же время, в отличие от матриц, они могут хорошо интерполироваться из одного положения в другое.
Являются-ли кватернионы лучшим решением, нежели остальные способы вращений (rotation formats)?
На сегодняшний день они комбинируют все сильные стороны других способов вращений. Но у них есть два слабых места, рассмотрев которые, мы придём к выводу, что кватернионы лучше использовать для промежуточных вращений. Итак, каковы недостатки кватернионов.
Во-первых кватернионы непросто отобразить на трёхмерном пространстве. И мы вынуждены всегда реализовывать вращение более простым способом, а затем конвертировать его. Во-вторых, кватернионы не могут эффективно вращать точки, и мы вынуждены конвертировать их в матрицы, чтобы повернуть значительное количество точек.
Это означает, что вы скорее всего не начнете или не закончите серию вращений с помощью кватернионов. Но с их помощью можно реализовать промежуточные вращения более эффективно, нежели при применении любого другого подхода.
«Внутренняя кухня» механизма кватернионов не очень понятна и не интересна мне. И, возможно, не будет интересна и вам, если только вы не математик. И я советую вам найти библиотеки, которые работают с кватернионами, чтобы облегчить вам решение ваших задач с их помощью.
Математические библиотеки «Bullet» или «Blender» будут хорошим вариантом для начала.
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://habr.com/ru/post/131931/
Отношение коллинеарных векторов
В данном разделе рассматриваются векторы, коллинеарные заданной прямой, т.е. принадлежащие или параллельные ей.
Согласно определению (см. разд. 1.1.2), при умножении данного вектора на число получаем вектор, коллинеарныи данному. Можно определить и «обратную» операцию — «деление коллинеарных векторов».
Отношением коллинеарных векторов и
называется действительное число, равное по модулю отношению длин этих векторов, положительное, если векторы
и
одинаково направленные, и отрицательное, если векторы
и
противоположно направленные:
По определению равенство эквивалентно равенству
для любых коллинеарных векторов
и
.
Например, найдем отношения коллинеарных векторов, изображенных на рис. 1.6:
Свойства отношений коллинеарных векторов
Для любых коллинеарных векторов справедливы следующие свойства:
1. Отношение любых коллинеарных векторов
и
определено однозначно.
2. Арифметические действия с отношениями коллинеарных векторов аналогичны действиям с числовыми дробями, а именно для любых коллинеарных векторов справедливы равенства
Докажем первое свойство. Предположим противное. Пусть и
, причем
. Тогда
и
, т.е.
, и следовательно,
. Разделив обе части равенства на число
, получим
, что противоречит условию
.
Докажем, например, последнее равенство (свойство 2,г). Пусть и
, тогда
и
. Надо доказать, что
. Найдем отношение длин векторов
. По определению получаем
, где знак плюс берется, если
, а минус — при
.
Если все векторы одинаково направлены, то , поэтому
.
Если и
, то
и
, так как
.
Если и
, то
и
.
Если и
, то
и
.
Таким образом, во всех случаях получаем , что и требовалось доказать.
Пример 1.4. Диагонали трапеции высекают на её средней линии
отрезок
(рис. 1.12). Найти отношения векторов
, если
Решение. По свойствам средних линий треугольника и трапеции находим отношения коллинеарных векторов:
(так как
);
(так как
);
(так как
).
Отсюда следуют соотношения
Теперь, используя свойства отношений коллинеарных векторов, получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Вектором называется направленный отрезок. Вектор обозначается либо символом 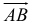
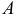
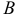

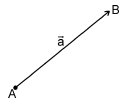
2. Длиной (модулем) вектора 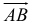
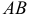
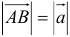
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 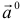


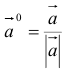
4. Вектор называется нулевым, если его начало и конец совпадают 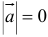
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 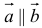

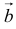
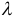
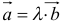
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 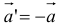

8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора 
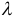
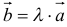
12. Для решения задач полезно знать также следующие законы и свойства:
Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки 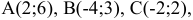
1) Найти координаты векторов
2) Написать разложение этих векторов по базису
3) Найти длины этих векторов
4) Найти скалярное произведение
5) Найти угол между векторами 
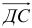
6) Найти разложение вектора 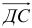

Решение:
1) Вычислим координаты векторов 
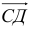
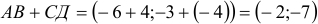
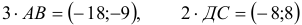
2)
3)
4) Для вычисления угла между векторами воспользуемся формулой:
5) Разложить вектор 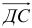

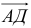
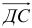

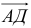
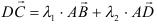
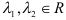
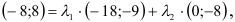
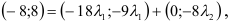
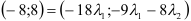
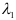
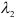
Задача:
а). Даны векторы 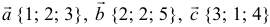
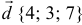
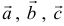
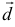
Решение:
Три вектора образуют базис, если 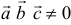
Найдем координаты вектора 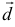
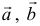
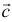
Два вектора равны, если их соответствующие координаты равны.
Решим систему методом Крамера:
Ответ: 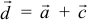
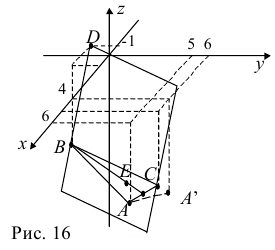
Задача:
Даны координаты вершин тетраэдра 



Решение:
1) Найдем координаты т. 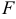
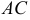
Точка 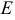
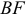
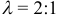
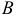
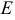
2) Найдем направляющий вектор прямой 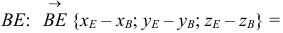
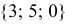

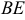
3) Найдем уравнение плоскости 
Найдем каноническое уравнение прямой, перпендикулярной плоскости 

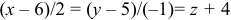
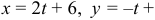
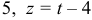
Найдем координаты точки 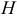

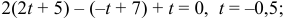
Координаты точки 


Ответ: 1) координаты точки пересечения медиан 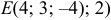
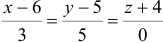
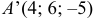
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 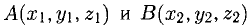
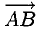
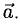
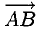
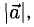
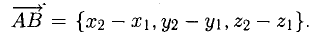
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 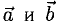
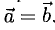
Векторы 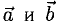
Вектор называется нулевым, если его модуль равен нулю, и обозначается
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало 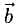
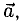
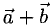
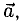
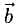
2.Если начала векторов 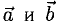

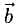

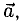
3.При умножении вектора
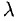
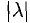
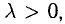
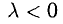
Вектор 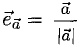
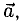
3°. Запись ci — 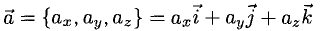


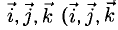
4°. Числа 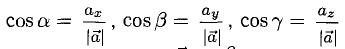

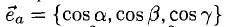

5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 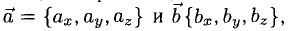
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 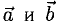
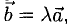
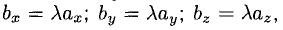
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 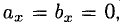
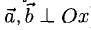
7°. Система векторов 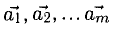
(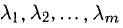

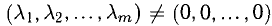
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 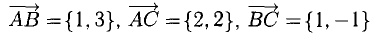
Найдем длины сторон: 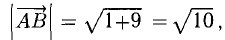
Нетрудно видеть, что 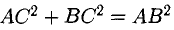
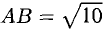
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
Имеем 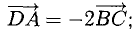
Пример:
Найти орт и направляющие косинусы вектора
Решение:
Имеем 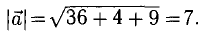
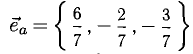
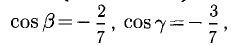
Пример:
Определить точку В, которая является концом вектора 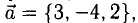
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
Следовательно, 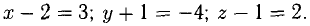
Пример:
Вектор 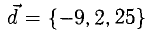
Решение:
Необходимо найти такие числа х, у, z, что 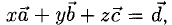
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
из которой
Ответ.
Пример:
Показать, что система векторов 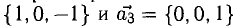
Решение:
В данном случае равенство (1) имеет вид 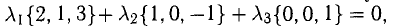
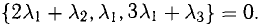
из которой следует, что 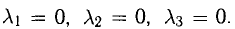
Пример:
Показать, что система векторов 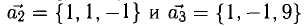
Решение:
Равенство (1) равносильно системе уравнений
Она имеет ненулевое решение, например, 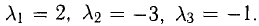
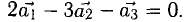
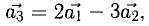
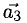
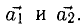
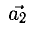
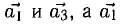
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 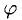
Из 
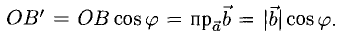
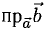

Итак,
2°. Если
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 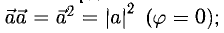
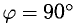
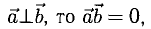
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
Примеры с решениями
Пример:
Перпендикулярны ли векторы 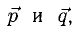
Решение:
Условие перпендикулярности векторов (п. 2°) 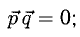
Ответ. Да.
Пример:
Найти проекцию вектора 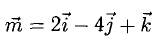
Решение:
Имеем 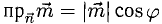
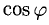
Ответ
Пример:
Зная векторы, совпадающие с двумя сторонами: 
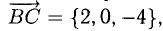
Решение:
Имеем (рис. 3.8)
При помощи таблиц находим 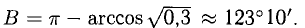
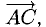
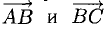
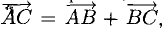
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
Найти координаты вектора 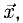
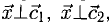
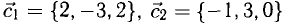
Решение:
На рис. 3.9 имеем 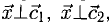
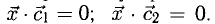
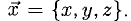
Векторное произведение векторов
1°. Векторы 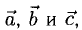
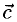
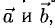
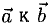
2°. Векторным произведением ненулевых векторов 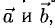
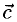
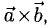
1)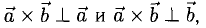
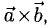
2) Вектор 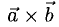
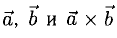
3) 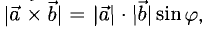
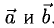
Если векторы 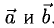
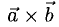
3°. Если известны координаты векторов-сомножителей 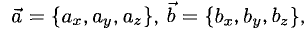
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В{3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 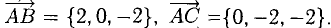
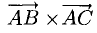
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 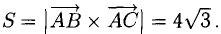
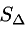
Пример:
Построить параллелограмм на векторах 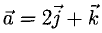
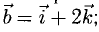

Сделаем чертеж (рис. 3.13). Имеем 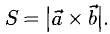
Следовательно,
Смешанное произведение векторов
1°. Смешанным произведением трех ненулевых векторов 
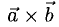
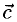
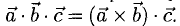

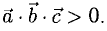

Модуль смешанного произведения векторов
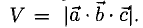
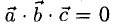

Объем тетраэдра с вершинами в точках 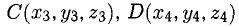
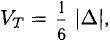
2°. Условие 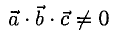

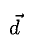
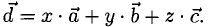
Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах
Решение:
Искомый объем 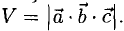
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 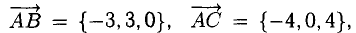
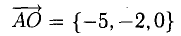
3) Площадь грани ABC
4) Объем пирамиды 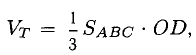
Ответ.
Основные понятия векторной алгебры
Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси 
Пусть М — произвольная точка оси 
Оnределение:
Ось 
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
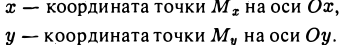
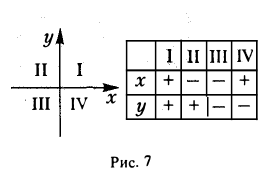
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:

Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
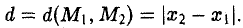
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
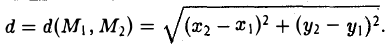
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
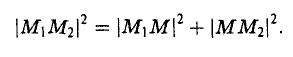
Так как расстояние d между точками M 1 и M 2 равно длине отрезка M1M2 а |M1M| = |x 2 — x 1|, |MM2| = |y 2 — y 1|, то отсюда получаем, что
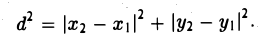
Замечая, что
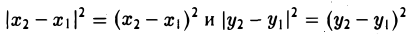
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 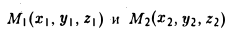
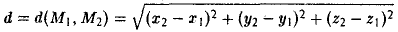
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
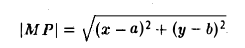
и возведем обе части полученного равенства в квадрат:
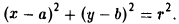
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
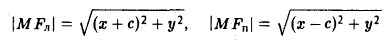
(рис. 13). Отсюда
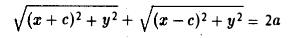
Перенесем второй корень в правую часть
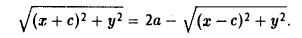
Возводя обе части в квадрат, после простых преобразований получим
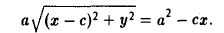
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
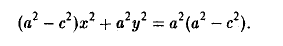
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b2 , nолучаем уравнение эллипса
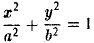
(см. главу 111) .
Деление отрезка в данном отношении:
Пусть М1 (х1 , y1) и М2 (х2 , y2) — различные точки плоскости. Пусть, далее, точка М(х, у) лежит на отрезке М1М2 и делит его в отношении λ 1 : λ 2 , т. е.
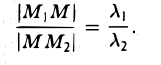
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
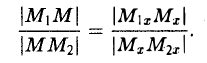
Так как
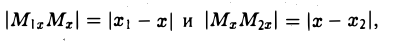
то из последних двух соотношений получаем, что
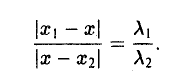
Точка М лежит между точками М1 и М2 , поэтому либо х 1 < х < х 2 , либо х 1 > х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
Отсюда

В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
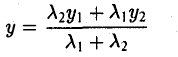
доказывается аналогичным рассуждением .
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
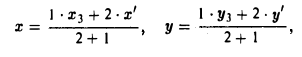
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
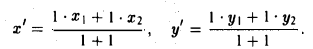
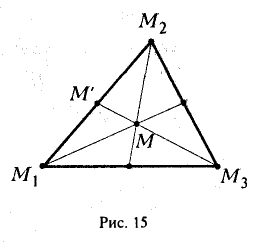
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
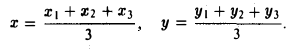
Замечание:
Если точка М(х,у,z ) делит отрезок с концами М1( х1, у1, z1) и М2( х2, у2, z2) в отношении λ1 : λ2, то ее координаты вычисляются по формулам
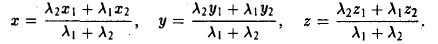
Полярные координаты
Предположим, что задана точка О, ось 
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси 
Точка О называется полюсом, 
Ясно, что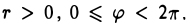
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный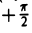
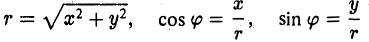
(рис.18). В свою очередь
Пример:
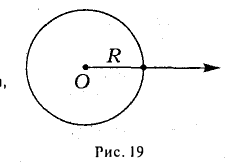
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г, <р) которых удовлетворяют равенству
r = R,
является окружностью радиуса R с центром в полюсе (рис. 19)
Определители 2-го и 3-го порядков
Пусть имеем четыре числа а11, а12, а21, а22 (читается — «а-один-один», «а-один-два», «а-два-один», «а-два-два»).
Определителем второго порядка называется число
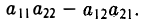
Обозначение:
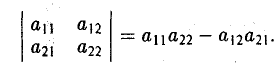
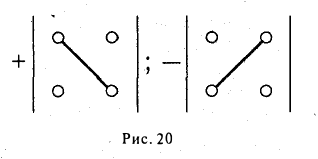
Числа а11, а12, а21, а22 называются элементами определителя; пары элементов а11, а12 и а21, а22 образуют строки определителя, а пары элементов а11, а21 и а12, а22 — его столбцы; пара элементов а11, а22 образует главную диагональ определителя, а пара а12, а21 — побочную диагональ.
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
Вычислить определитель
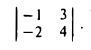
По правилу (1) имеем
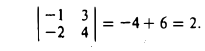
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
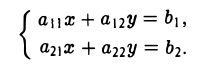
Решая эту систему методом исключения неизвестных при условии, что
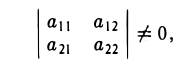
находим
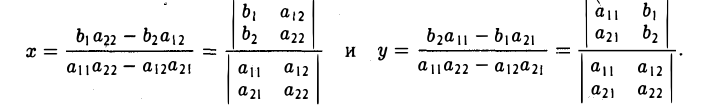
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом

и вычисляемое по следующему правилу:
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
Элементы а11, а22, а33 образуют главную диагональ определителя ∆, элементы а13, а22, а31 — побочную диагональ, элементы а13, а22, а31 — побочную диагональ.
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
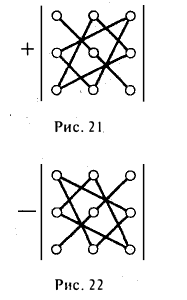
Пример:
Вычислить определитель

Применяя правило треугольника, находим
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
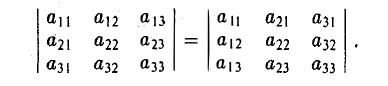
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
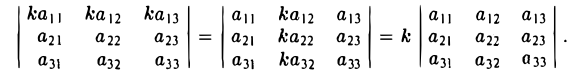
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка

Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
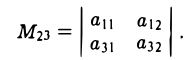
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
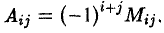
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
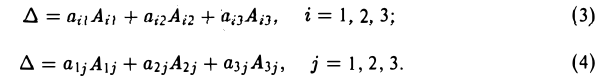
Покажем, например, что
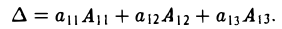
Пользуясь формулой (2), получаем, что
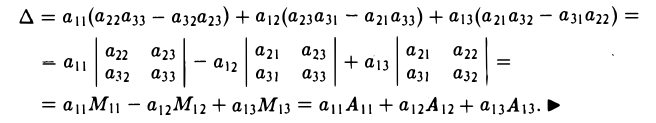
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Вычислить определитель
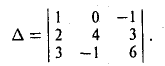
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
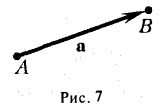
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
А В = CD.
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор 
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой

(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 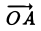


Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
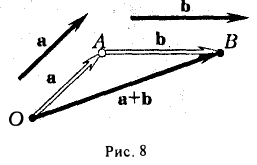
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор 
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 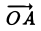

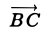

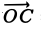
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
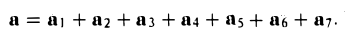
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
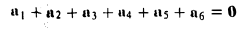
(рис. 15).
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
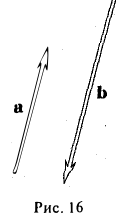
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 

Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
- |Ь| = |λ| • |а|;
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ < 0).
Обозначение: b = λа.
При λ = 0 положим λа = 0.
Таким образом, векторы а и Ь = λа коллинеарны по определению. Верной обратное: если векторы а(а ≠ 0) и Ь коллинеарны, то можно найти число А такое, что h = λа.
Укажем основные свойства этой операции умножения вектора на число:
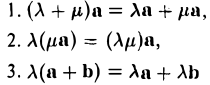
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
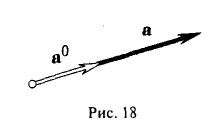
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
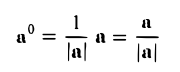
есть единичный вектор (орт) направления вектора а (рис. 18).
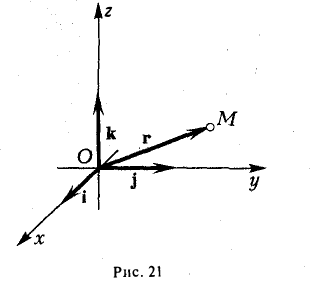
Координаты и компоненты вектора
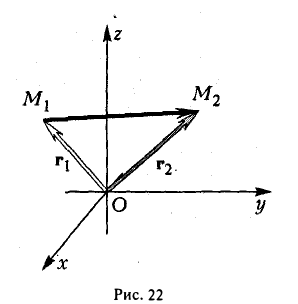
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что

Векторы 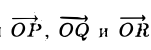
поэтому найдутся числа х, у, z такие, что
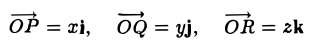
и, следовательно,
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = {х, y,z}.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = { х1, у1, z1 } и b = {х2, у2, z2} равны тогда и только тогда, когда соответственно равны их координаты, т. е.
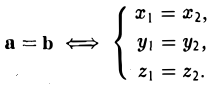
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
Пусть имеем два вектора а = { х1, у1, z1} и b = { х2, у2, z2 },так что а = х1i, у1j+ z1k. b = х2i+ у2j+z2k. На основании правила сложения векторов имеем
или, что то же,
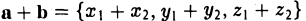
— при сложении векторов их координаты попарно складываются. Аналогично получаем
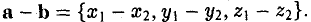
Далее,
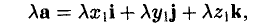
или, что то же,
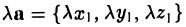
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 } — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
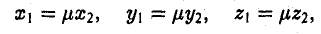
или (3)
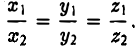
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Пример:
Найти координаты вектора 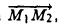
Из рис. 22 видно, что 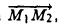
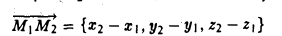
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор 
Определение:
Проекцией вектора 
Обозначение:
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Например,
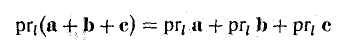
(рис. 26).
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
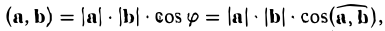
(1)
где φ, или в иной записи (
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
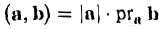
(рис. 27 б) и, аналогично,’ (2)
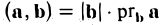
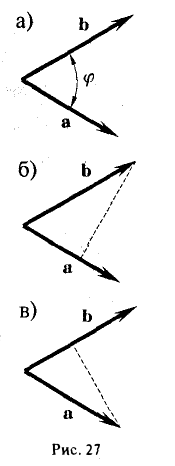
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
Действительно,
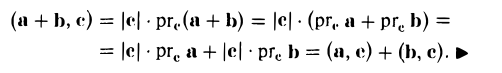
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
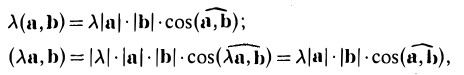
поскольку при λ > 0 углы (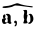
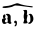
Аналогично рассматривается случай λ < 0. При λ = 0 свойство 4 очевидно.
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
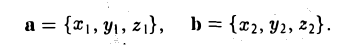
Рассмотрим скалярное произведение векторов а и b:
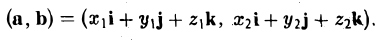
Пользуясь распределительным свойством скалярного произведения, находим
Учитывая, что
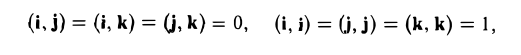
получаем (4)
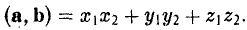
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а2.
Применяя формулу (4) при b = а, найдем (5)
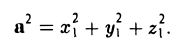
С другой стороны,
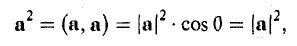
так что из (5) следует, что (6)
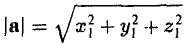
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
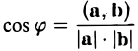
(предполагается, что векторы а и b — ненулевые).
Пусть а = { х1, у1, z1}, b = { х2, у2, z2 }. Тогда формула (7) примет следующий вид
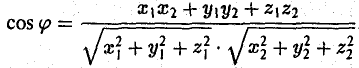
Пример:
Найти угол между векторами a = {2, -4,4,} и d = {-3,2,6}. Пользуясь формулой (8), находим
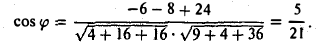
Пусть b = i, T.e. b = {1,0,0}. Тогда для всякого вектора а = { х1, у1, z1} ≠ 0 имеем
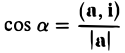
или, в координатной записи, (9)
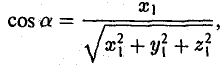
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
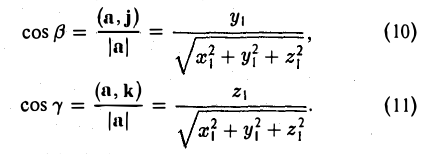
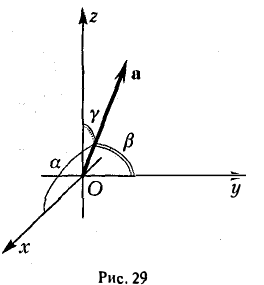
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
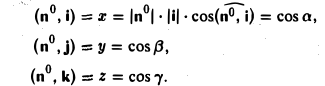
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
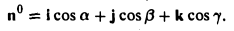
Отсюда получаем
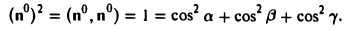
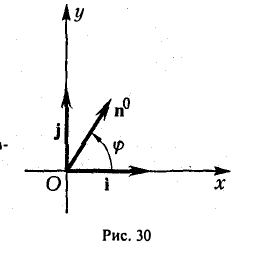
Пример:
Пусть единичный вектор n° ортогонален оси z:
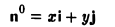
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Тем самым,
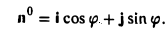
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
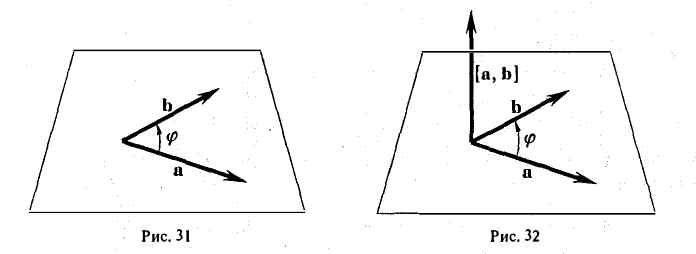
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
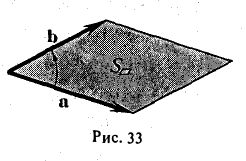
По определению длина векторного произведения (1)
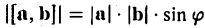
численно равна площади 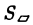
|[a, b]| = 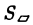
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
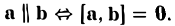
2. Векторное произведение антикоммутативно, т. е. всегда (2)
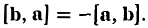
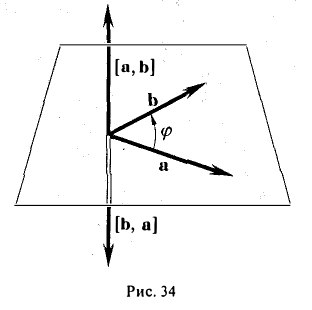
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = { х1, у1, z1}, b = { х2, у2, z2 }. Пользуясь распределительным свойством векторного произведения, находим (3)
Выпишем векторные произведения координатных ортов (рис. 35):
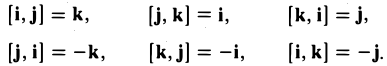
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
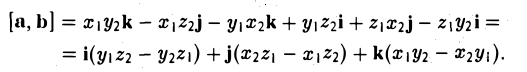
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
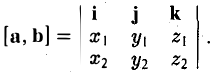
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 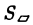
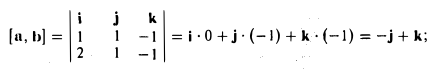
откуда
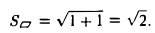
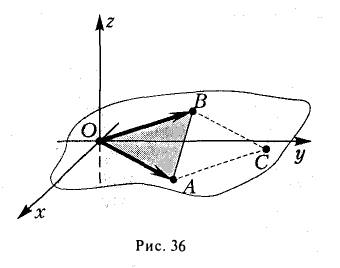
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a=

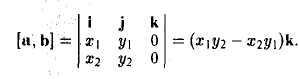
Отсюда
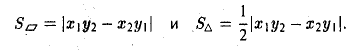
Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
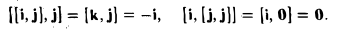
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
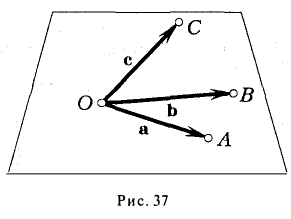
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 
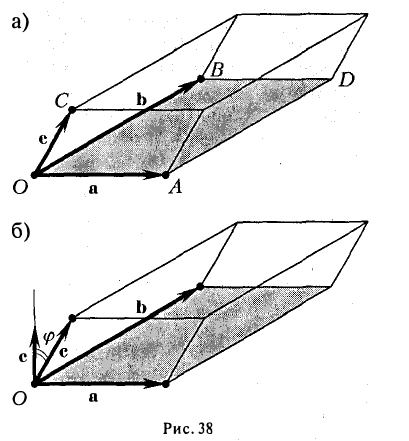
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
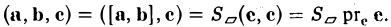
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
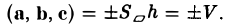
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
{а, b, с компланарны} <=> (а, b, с) = 0.
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
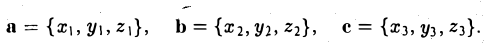
Найдем выражение для их смешанного произведения (а, b, с). Имеем
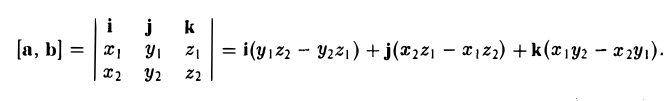
Откуда
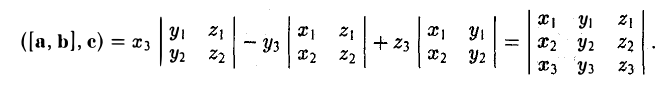
Итак,
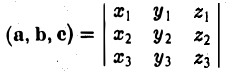
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Необходимое и достаточное условие компланарности векторов а = { х1, у1, z1}, b = { х2, у2, z2 }, c = { х3, у3, z3} запишется в следующем виде
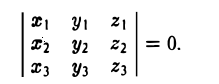
Пример:
Проверить, компланарны ли векторы
a = {7, 4,-6}, b = {2, 1,1}, с ={19, 11,17}.
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
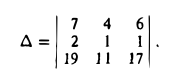
Разлагая его по элементам первой строки, получим
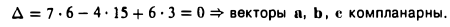
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
План урока:
Разложение векторов
Координаты векторов
Сложение и вычитание векторов
Признак коллинеарности векторов
Разложение векторов
Заметим, что если два вектора a и b коллинеарны, то обязательно найдется такое число k, для которого будет справедливо равенство:
Длина а составляет 6 клеток, а длина b – 9 клеток, при этом они сонаправлены. Получается, что b длиннее a в 9/6 = 1,5 раза, а потому можно записать:
Мы смогли выразить b через а. Иначе можно сказать, что мы разложили вектор b по вектору a. Можно и наоборот, выразить b через a:
Теперь посмотрим на вектора с и d. Их длины составляют 4 и 8 клеток, то есть отличаются в 2 раза, при этом они противоположно направлены. Поэтому эти вектора можно выразить так:
Обратите внимание, что выразить, например, а через с не удастся. Действительно, предположим, что есть такое число k, что
Тогда, по определению операции умножения вектора на число, вектора а и c должны быть коллинеарными, но они таковыми не являются.
Вектор можно раскладывать не на один, а на два вектора, которые ему не коллинеарны. Покажем это на примере:
Здесь вектора р, а и b не коллинеарны, при этом р выражен через а и b:
В данном случае говорят, что р разложен на вектора а и b, а числа 2 и 4 именуют коэффициентами разложения.
Верно следующее утверждение:
Продемонстрируем, как можно осуществить такое разложение. Пусть заданы вектора с, а и b, и требуется разложить c на а и b:
На первом шаге просто отложим все три вектора от одной точки. Далее построим прямые, проходящие через вектора а и b:
Далее через конец вектора с проведем прямые, параллельные построенным на предыдущем шаге прямым. В результате у нас получится некоторый параллелограмм АВСD:
Заметим, что вектор с оказался диагональю в этом параллелограмме. Тогда, согласно правилу параллелограмма, можно записать:
Ясно, что вектора АВ и b коллинеарны, так как лежат на одной и той же прямой. Тогда найдется такое число k, для которого будет верно отношение:
Конкретно в данном случае видно по рисунку, что АВ вдвое длиннее вектора b, поэтому
Аналогично коллинеарными являются вектора а и АD, поэтому существует число m, при котором справедливо равенство:
Понятно, что числа k и m определяются единственным образом. В общем случае они могут быть не только целыми, но и дробными (в том числе иррациональными) и даже отрицательными числами. Проще говоря, они могут быть любыми действительными числами.
Задание. Найдите коэффициенты разложения вектора d на вектора e и f:
Решение. Отложим все три вектора от одной точки. Далее проведем прямые, на которых лежат вектора e и f:
Теперь через конец d проводим ещё две прямые, параллельные двум уже построенным прямым, и в результате получаем параллелограмм:
Вектор d можно представить в виде суммы:
Особняком стоит случай, когда раскладываемый вектор коллинеарен одному из тех векторов, на которые он раскладывается. В этом случае один из коэффициентов разложения оказывается равным нулю. Например, пусть с надо разложить на а и b:
Строить параллелограмм в данном случае не нужно. Так как а и с коллинеарны, то найдется некоторое число k, при котором будет выполняться равенство:
Координаты векторов
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:
Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.
Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.
Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:
Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:
Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:
Можно записать равенство:
Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:
Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i. Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.
В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).
Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.
Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:
Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:
После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:
После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты {1; – 3}.
Выполним построение и для с:
Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют {3,5; 0}.
Осталось рассмотреть d:
Здесь координаты вектора будут равны {– 2,5; – 2,5}, так как такие же координаты имеет точка D.
Ответ: а{4;3}; b{1; – 3}; с{3,5; 0}; d{– 2,5; – 2,5}.
Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.
Задание. Даны координаты вектора:
Постройте по три вектора, имеющие заданные координаты.
Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:
Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:
Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:
Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:
Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).
Сложение и вычитание векторов
Пусть у нас есть векторы a{x1; у1} и b{x2; у2}. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:
Эта запись означает, что с имеет координаты {х1 + х2; у1 + у2}. В результате мы можем сформулировать правило сложения векторов:
Проиллюстрируем правило на примере. Пусть надо сложить вектора а {2; 3} и b {4; 5}. Понятно, что в результате получится новый вектор, который мы обозначим как с {х; у}. Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:
x = 2 + 4 = 6
Для нахождения второй координаты складываем соответственно вторые координаты векторов:
y = 3 + 5 = 8
В итоге получился вектор с {6; 8}.
Задание. Сложите вектора, имеющие координаты:
Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):
Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a{x1; у1} и b{x2; у2}. Снова запишем их разложение на единичные вектора:
Теперь мы можем сформулировать правило вычитания векторов:
Например, пусть надо вычесть из вектора а{5; 3} вектор b{2;1}. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:
x = 5 — 2 = 3
Аналогично вычисляем и координату у:
y = 3 — 1 = 2
В итоге получили вектор с координатами {3; 2}.
Задание. Вычтите из вектора а вектор b, если известны их координаты:
Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):
Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х1и у1 можно разложить на орты следующим образом:
Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.
Например, есть вектор а{3; 7}, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:
x = 5*3 = 15
y = 5*7 = 35
В результате получился вектор {15; 35}.
Задание. Умножьте вектор а на число k, если известно, что:
Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:
Признак коллинеарности векторов
Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что
Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:
x1 = k * x2
y1 = k * y2
Если числа х2 и у2 не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:
Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.
Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.
Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:
24:8 = 3
Получили число 3. Далее поделим и координаты у:
15:5 = 3
Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:
В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:
Естественно, снова получилось одинаковое число.
Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у1}, причем у1≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x2; у2} составят:
Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у2 и у1 могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие
y2 = ky1
Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,
Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:
Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.
Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.
Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:
Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:
Числа различны, поэтому вектора НЕ коллинеарны.
В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.
е) {0; 5} и {0; 12}
У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.
ж) {0; 3} и {2; 6}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
з) {9; 0} и {4; 0}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
и) {0; 3} и {12; 0}
Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.
к) {0; 0} и {5; 8}
Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.
Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.
Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор — основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.
Векторы обозначают малыми латинскими буквами с чертой сверху 


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 





Учитывая, что 

Вычитание векторов сводится к сложению противоположного вектора
Запишем основные свойства действий сложения векторов:
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 
Умножение вектора на число
Произведением вектора 


а) 
б) 




Запишем основные свойства действий умножения вектора на число:
Скалярное произведение векторов
Скалярным произведением 






Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 

Наоборот, если 

Например, скалярное произведение 
Запишем основные свойства действий скалярного умножения векторов:
Векторное произведение
Векторным произведением 



1) модуль вектора 


2) вектор 


3) вектор 





Модуль векторного произведения равен площади параллелограмма, построенного на векторах 







Приведём основные свойства векторного произведения:
1) векторное произведение 


2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный: 
3) 
4) 
Физическое содержание векторного произведения такое. Если 







Смешенное произведение векторов
Смешенным произведением векторов 



Как результат скалярного произведения векторов 


Действительно, 




Объём V параллелепипеда, построенного на векторах 
Однако, знак смешенного произведения совпадает со знаком 




Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2)
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов 
Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство:
Решение.
Пусть 



тогда
Пример 2.
У прямоугольного параллелепипеда рёбра 




Решение.
Пусть 

рис. 9.
Далее,
Этим закончен «перевод» условия задачи на «язык» векторов.
Теперь произведём вычисления с векторами:
Наконец «переводим» полученные вектора равенства снова на «геометрический язык». Поскольку 

Далее поскольку 




Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор 



Доказательство.
Пусть векторы 





Тогда по правилу параллелограмма 
Но 

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают 
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор 




Доказательство.
От точки О отложим векторы 


в котором вектор 
Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают 






Отсюда легко установить длину вектора как расстояние между двумя точками:
Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:
Действительно:
2. При вычитании векторов соответствующие координаты вычитаются:
Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора 

4. Скалярное произведение двух векторов 
Правда:
Поскольку 

5. Векторное произведение векторов 
6. Смешенное произведение трёх векторов 
Пример 1.
Зная координаты векторов 

Решение:
Ответ: 
Пример 2.
Зная координаты векторов 

Решение.
Ответ: 
Пример 3.
Зная координаты векторов 
а) скалярное произведение векторов
б) векторное произведение векторов
в) смешенное произведение векторов 
Решение.
Ответ:
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов
1. Угол между векторами.
2. Условие перпендикулярности двух векторов:
(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов: 
4. Условие компланарности трёх векторов.
(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка 

Если точка М делит отрезок АВ на пополам то 
Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора 

который имеет длину 

Рис. 12.
Условие 
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов 






Рис. 13.
Понятно, что вектор 


Для векторной суммы справедливый переместительный закон
Легко убедиться, что для векторной суммы имеет место соединительный
закон 
Исходя из определения 2, легко находим сумму, например, четырех векторов 
Рис. 14.
Вектор 


в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью 



Рис. 15.
Как видно из рис. 15, одна диагональ 




Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов 


Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор 
Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора 


Определение 1. Проекцией вектора 
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор 


Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция 

Свойства проекций.
1. Если векторы 


2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:
3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:
4. Если вектор 

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор 
Пусть 
Проекции x, y, z вектора 

Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора 
x = x2 – x1, y = y2 – y1, z = z2 – z1 .
Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но 
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор 
Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор 


Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому


Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим
Отсюда для направляющих косинусов получаем

Для направляющих косинусов справедливо равенство 
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .
Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через 
Спроецируем вектор 
Из прямоугольника ODMC видно, что вектор 

Тогда

Вектор 
Векторы 




Подставляя эти значения в равенство (2.10), учитывая, что 

Слагаемые 

Тройка векторов 

Пример 1. Построить вектор 
Рис. 20.
Решение. Компоненты вектора 


соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы 





Сложив эти равенства, получим

Итак, координаты вектора 
Правило 2. Чтобы отнять от вектора 



Правило 3. Чтобы умножить вектор 


Пример 1. Найти вектор 
Решение. Выполним действия последовательно и найдем

Значит,
Вектор — основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются 
Определение 2. Длиной (или модулем) вектора 


Длина вектора 


Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы 

Если ненулевые векторы 







Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: 





Определение 4. Векторы 



Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора 








Теорема 2. Сумма 




Правило треугольника можно сформулировать и так: для любых трёх точек 
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: 




Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1)
2) 
3) 
Здесь 
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору 
Определение 6. Разностью двух векторов 



Разность векторов 



Разность векторов 



Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора 








Таким образом, по определению, 






Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
— ассоциативность (сочетательный закон);
-
—дистрибутивность относительно сложения векторов (1-й распределительный закон);
-
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь 


Справедлива также и лемма о коллинеарных векторах: если векторы 


что 

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть 



Доказательство
1. Из равенства 





2. Пусть 




З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы 




Доказательство
1. Пусть векторы 
точки 
















Докажем, что векторы 






Отложим от произвольной точки 







Если векторы 






Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор 




2. Пусть векторы 





















3. Докажем теперь, что разложение вектора 



Тогда
отсюда
— т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор 





Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора 












Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
получаем
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
и действительного числа
получаем
Докажем, например, свойство 2. Так как 



Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов 

Определение 11. Скалярным произведением векторов 

Теорема 8. Два ненулевых вектора 

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора 


Так как 
Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:
Если векторы 


Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.
Доказательство. Отложим от произвольной точки 







итак как 


поэтому
Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды 






Решение (см. рис. 14).
1. 

2. Так как 


Ответ:
Заметим, что в разложении вектора 








Задача 2.
Пусть 


Решение (см. рис. 15). Пусть 






Ответ:
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов 



Суммой 






Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)
2) связующий
3) для каждого вектора 

4)
5) для некоторых двух векторов 

Если вектор 



Пусть вектор имеет начало в точке 





Если вектор 
Произведением вектора 






Любой вектор 
где 



Пример 1.73
Даны два вектора: 

Найти вектор
Решение
Признаком колинеарности двух векторов 

Скалярным произведением двух векторов 


Скалярное произведение можно записать в таком виде:
Если векторы 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами 

Отсюда получается условие перпендикулярности двух векторов: если 

Среди свойств скалярного произведения отметим так:
Векторным произведением вектора 


1) длина вектора 
2) вектор 

3) из конца вектора 


Заметим, что 


В координатной форме векторное произведение векторов 

Смешанным или скалярно — векторным произведением трех векторов 



Если векторы 
Если известные координаты сомножителей 
Если три ненулевых 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:
Решение примеров:
Пример 1.74
Заданы координатами точек 


1) вектор 
2) угол между векторами 
3) координаты вектора
4) объем пирамиды с вершинами в точках
Решение
1) По формуле (1.14) находим
тогда
2) Косинус угла между векторами 

Поскольку косинус угла отрицательный, то угол 
3) Координаты векторного произведения находим по формуле (1.22):
4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:
Тогда объем пирамиды
Собственные числа и собственные векторы
Вектор — столбец 




Тут 



Координаты собственного вектора 

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы
Решение. Характеристические уравнения данной матрицы имеет вид (1.24):

отсюда получается, что матрица 





которое приводится к одному уравнению
Возьмем 
Следует, первый собственный вектор является
Второй вектор 

Эта система уравнений так же приводится к одному уравнению 


Таким образом, матрица 




Пример 1.91
Найти собственные векторы и собственные значения матрицы
Решение. Характеристическое уравнение
Раскрыв определитель получим:
Корень 


Система уравнений для определения собственных векторов имеет вид:
Последовательно подставим 

Фундаментальная система уравнений получается, если свободным переменным 
Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению 
Фундаментальная система решений получается, если взять
Векторная алгебра
Понятие «вектор» (от лат. vector — носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия — математическая наука, объектом изучения которой являются геометрические фигуры, а предметом — установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) — французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в 






алфавита с чертой: 
Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство — где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов:
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором 
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору 

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы 



1. Суммой векторов 


Параллельный перенос можно осуществить и так, что объединятся начала векторов 

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):
Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:
2) соединительная, или ассоциативная:
3)
4)
Разницу 

Умножения вектора на скаляр
Пусть 










Рис. 6.4
При


Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

2) соединительный, или ассоциативный закон:

3) распределительный или дистрибутивный закон:

4)
5)
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора 

Известно, что три ненулевые векторы 


Рассмотрим понятие, имеет очень важное значение в теории векторов — проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление — отрицательным).
Компонентой вектора 





Рис. 6.5
Проекцией вектора 






Основные свойства проекции вектора на ось
1. Проекция вектора на ось 

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:
Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:
Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве 


Рис. 6.6
Выберем в пространстве произвольную точку 





Под декартовыми прямоугольными координатами точки 

Точка 





Измерениями параллелепипеда есть модули координат точки 
Углы 


откуда:
Косинусы направляющих углов называются направляющими косинусами радиус-вектора 
1) направляющие косинусы являются координатами единичного радиус-вектора:
2) сумма квадратов направляющих косинусов вектора 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало 
Координатами любого вектора 



Задача вектора тройкой его координат 
Для единичных векторов 

Длина произвольного вектора 
Найти длину и направляющие косинусы вектора
По формулам (6.5) имеем:
Установим связь между координатами вектора — числами — и его компонентами — векторами — с помощью единичных векторов 
Рис. 6.7
Компонентами вектора 


Следовательно, любой вектор 
Изображение вектора с 
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с 


Действительно, по свойствам ассоциативности и дистрибутивности имеем:
2. При умножении вектора 

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:
Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов 



Вместо 


Для определения угла 







Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение 
2. Скалярный квадрат вектора равен квадрату его модуля, то есть
3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:
4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:
Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов 

1. Вычислим скалярные произведения единичных векторов 

2. Находим произведение 
Раскрываем скобки и получаем:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения 
Как следствие из (6.12) при 
Определим угол между двумя ненулевыми векторами 

Следовательно, косинус угла между двумя векторами определяется формулой:
Отсюда
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:
Критерием коллинеарности векторов 

Векторное произведение двух векторов
Пусть 








1) модуль его численно равен площади параллелограмма, построенного на векторах 

2) он перпендикулярный плоскости параллелограмма 



Рис. 6.9
Векторное произведение обозначается символами: 
Следовательно,
где 




Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы 

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:
Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:
где
Векторное произведение векторов 

1. Определяем векторные произведения ортов 
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:
Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:
Рис. 6.10
Рассмотрим, например, произведение 




2. Находим произведение 
Множители при 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора 


Если символы 

Найдем векторное произведение векторов 
Модуль векторного произведения 

Смешанным произведением трех векторов 


Смешанное произведение можно обозначать тройкой векторов 





Геометрическая интерпретация смешанного произведения. Пусть 

Рис. 6.11
Вектор 





Согласно (6.11) скалярное произведение 



где 




Модуль смешанного произведения трех векторов численно равен объему параллелепипеда 
Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три — компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

Свяжем с изображенными на плоскости векторами 
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:
Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы 
Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:
Векторы 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки 
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка 

1. Введем в рассмотрение вектор 



2. Определим координаты вектора 


3. Находим модуль вектора 

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин:
По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник 



1. Введем в рассмотрение векторы:
и найдем их векторное произведение
По соотношению (6.20) имеем:
2. Вычислим модуль вектора 


Тогда для площади треугольника 
Знак 

Если треугольник принадлежит не плоскости 
Найдем площадь треугольника с вершинами 

Введем в рассмотрение векторы: 


Тогда

Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки 







Рис. 6.15
Число 
называется отношением, в котором точка 



Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки 




Пусть точкам 




С этого векторного равенства найдем вектор
или в координатах:
Отсюда, если отрезок разделить на две равные части точкой 

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин 
Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций

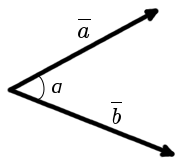
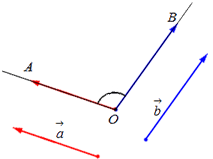
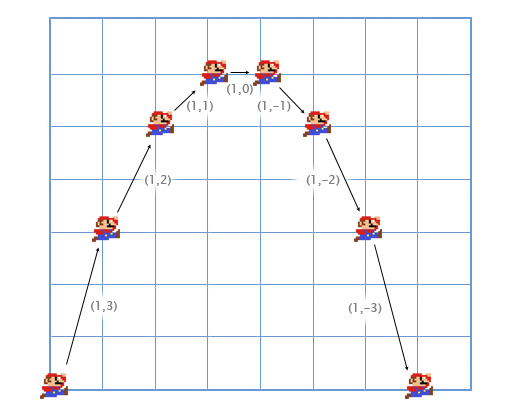
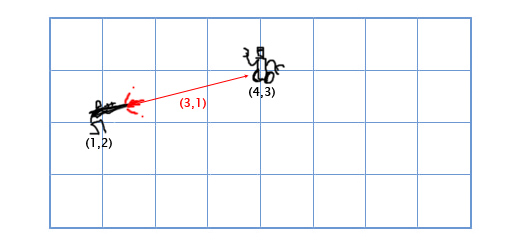

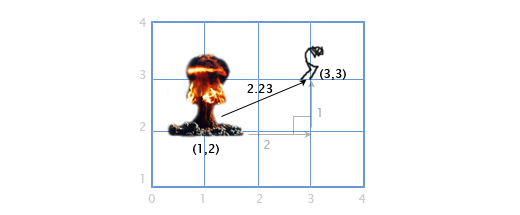
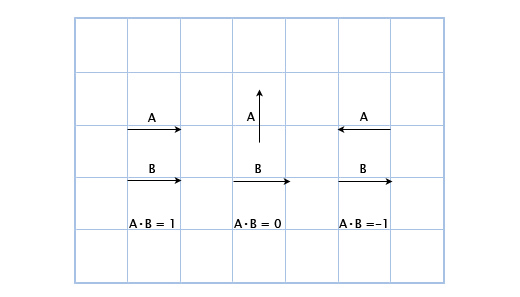
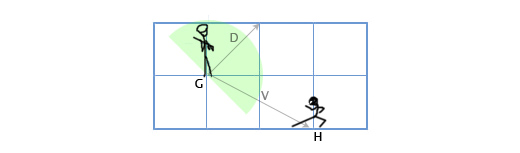
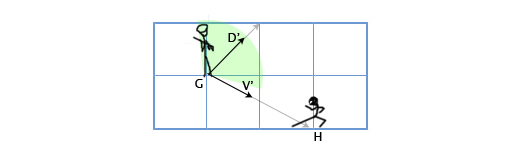
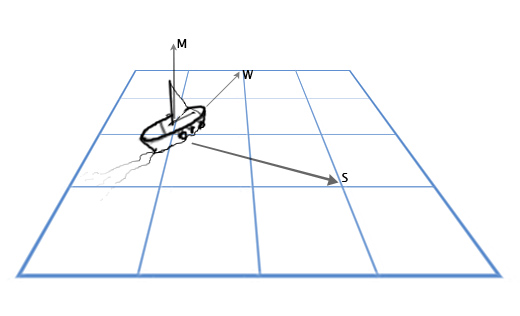
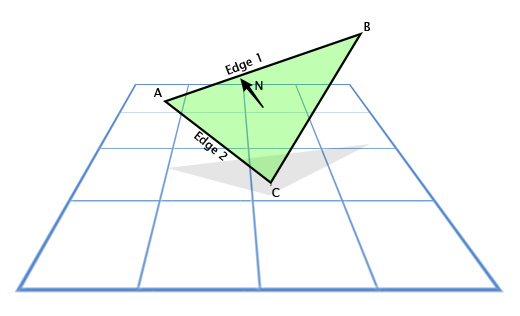
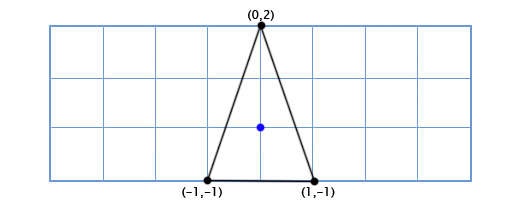
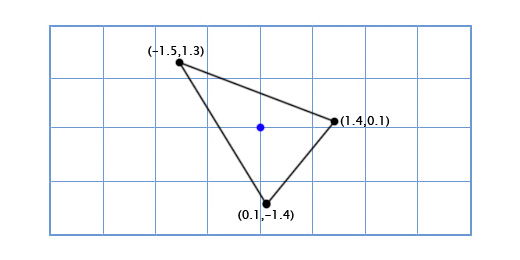
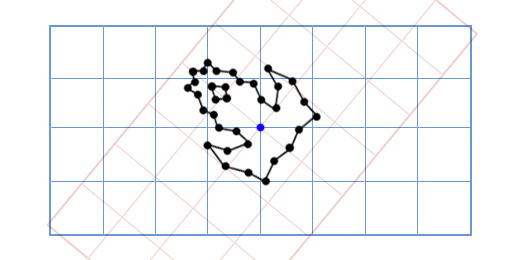
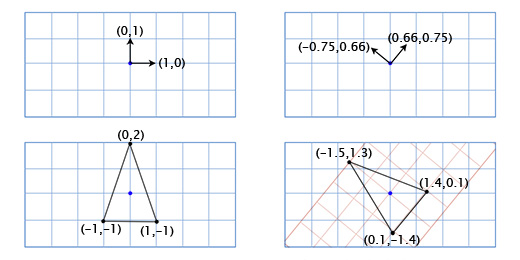
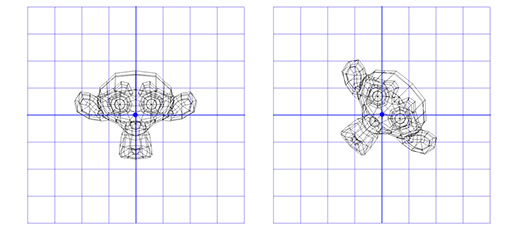
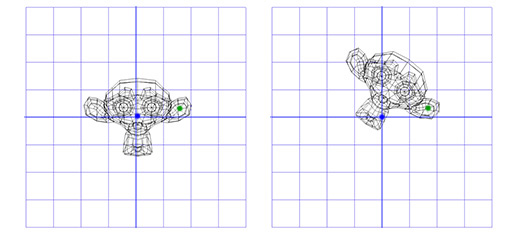
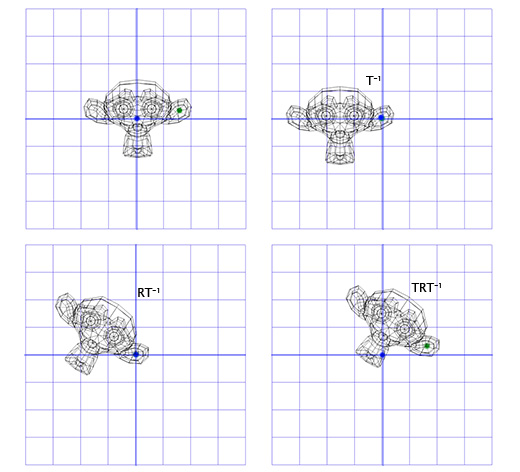
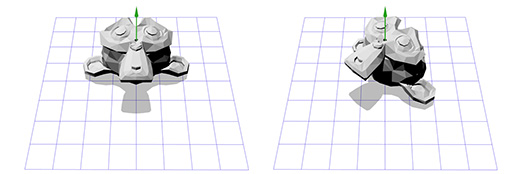
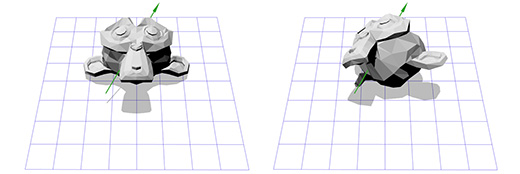
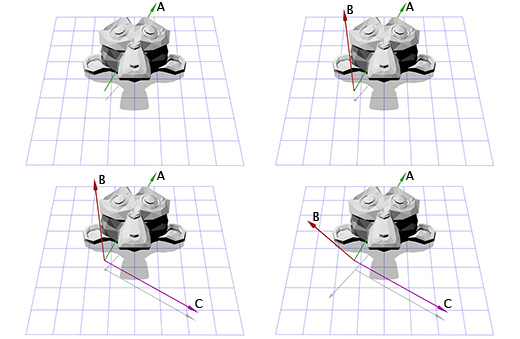
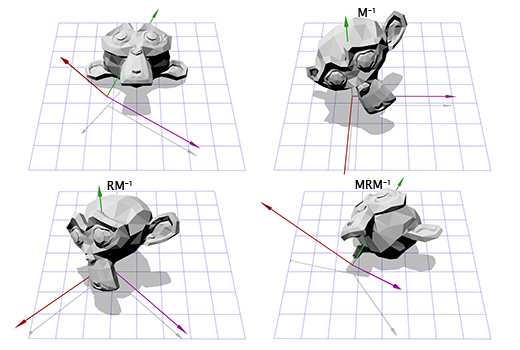
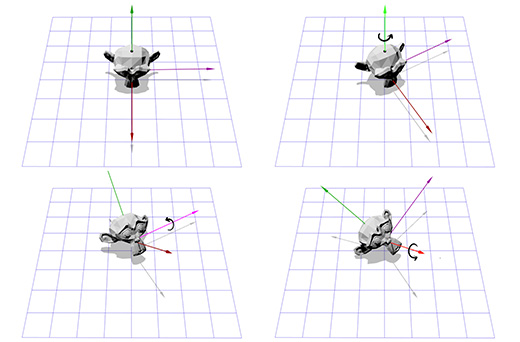


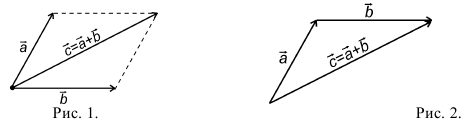
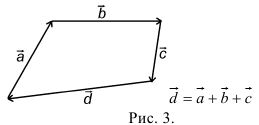

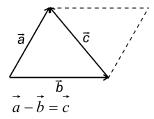
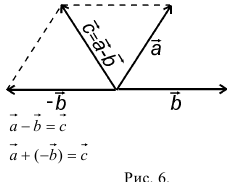

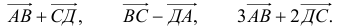
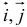
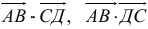
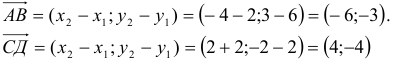
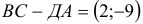
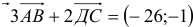
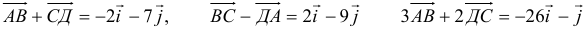
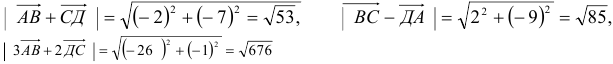
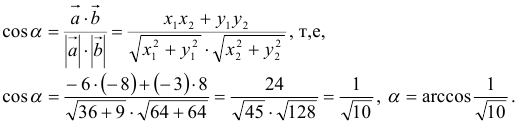
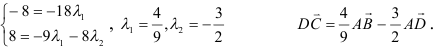
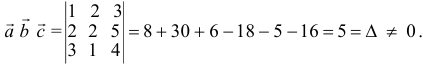
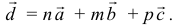
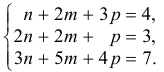
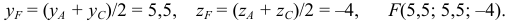
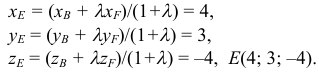
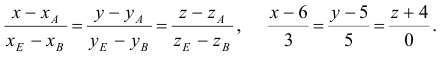
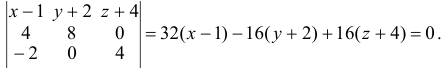
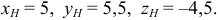
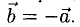
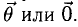
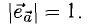
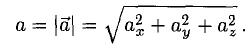
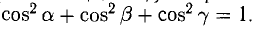
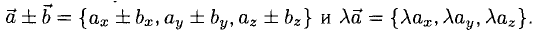
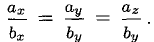
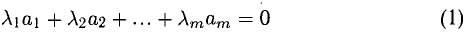
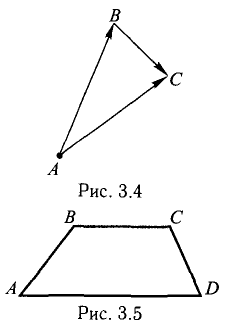
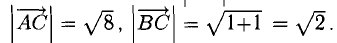
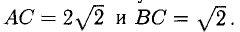
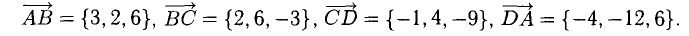
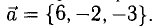
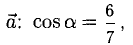
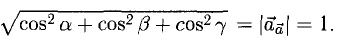
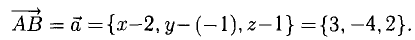
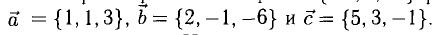
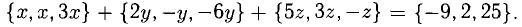
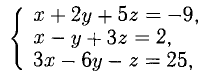
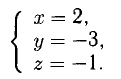
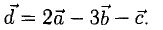
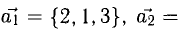
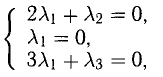
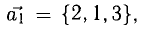
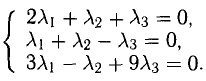
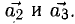
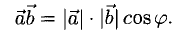
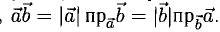
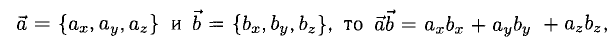
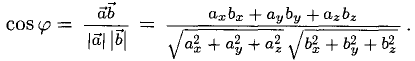
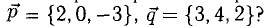
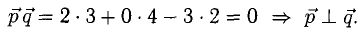
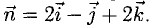
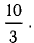
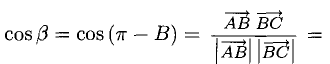
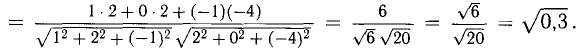
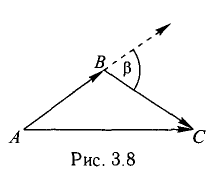
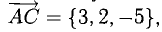
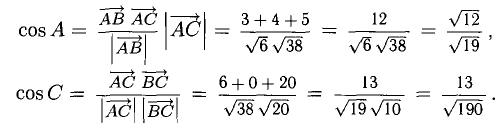
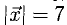
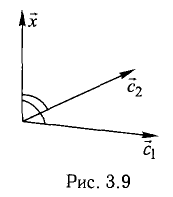
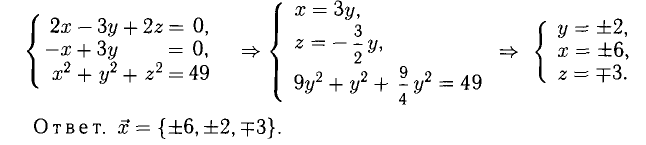
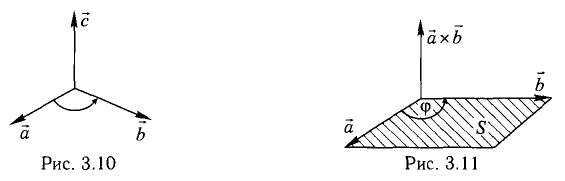
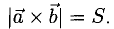
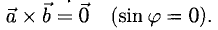
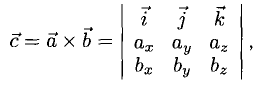
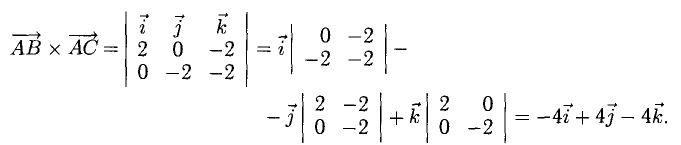
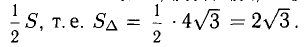
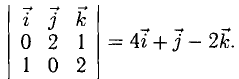
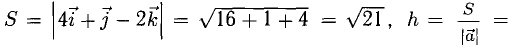
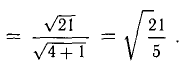
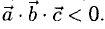
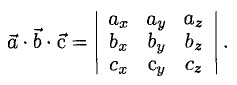
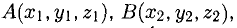
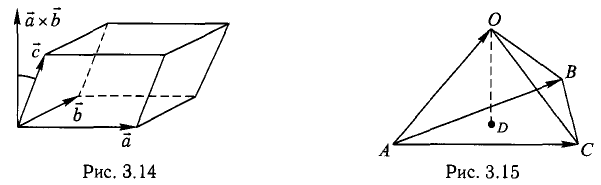
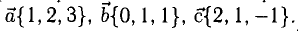
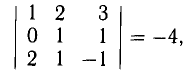
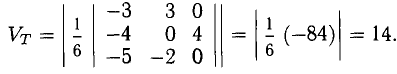
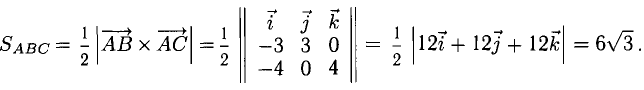
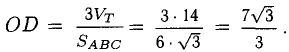

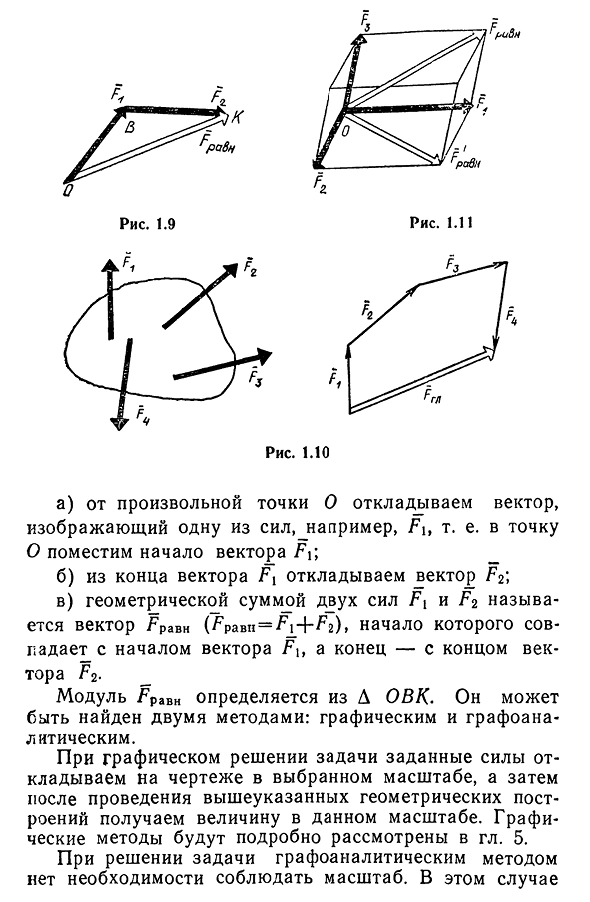



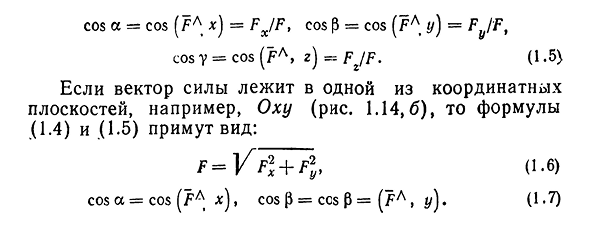


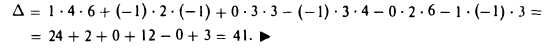
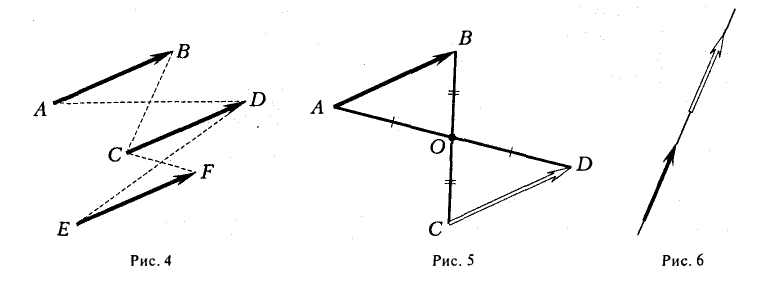
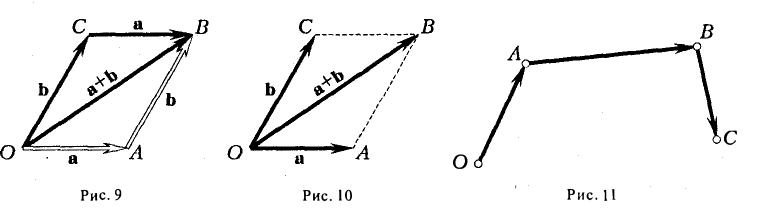
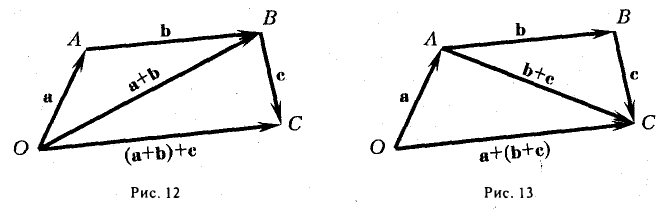
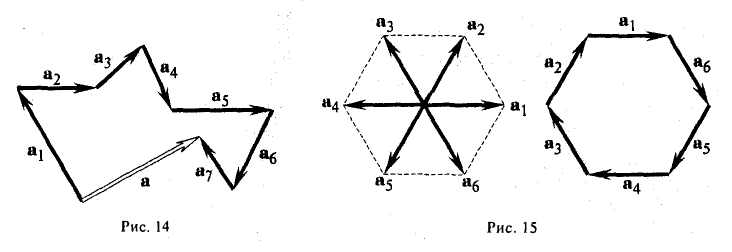
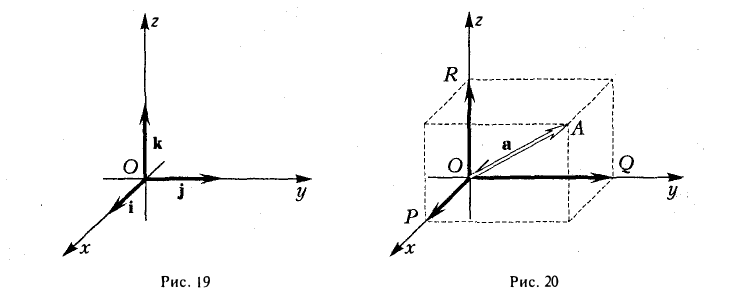
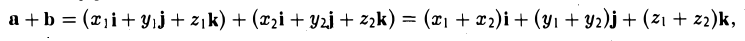
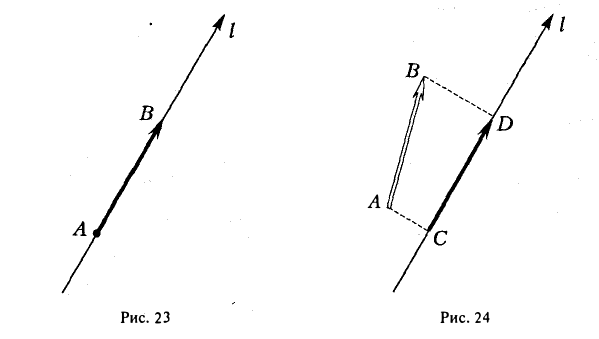
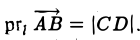
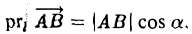
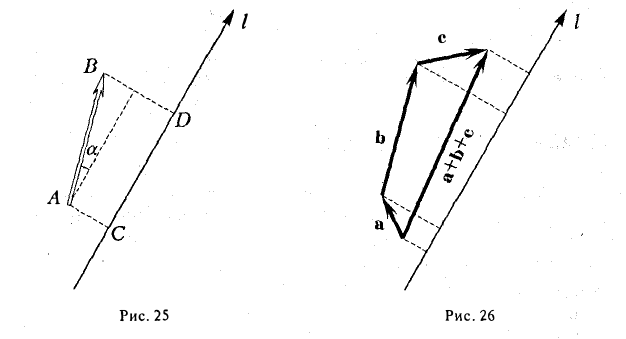
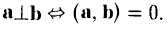
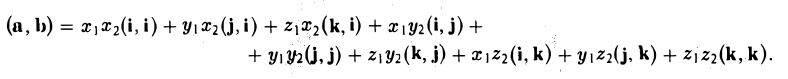
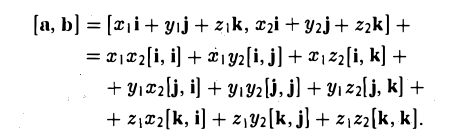

























































































































































 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).











 отсюда
отсюда 
 — т. е. векторы
— т. е. векторы  компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора  по данным векторам
по данным векторам  единственно. Теорема доказана.
единственно. Теорема доказана.

 получаем
получаем 
 и действительного числа
и действительного числа  получаем
получаем 











































































































































































































